【华为OD机试真题 Python】创建二叉树
前言:本专栏将持续更新华为OD机试题目,并进行详细的分析与解答,包含完整的代码实现,希望可以帮助到正在努力的你。关于OD机试流程、面经、面试指导等,如有任何疑问,欢迎联系我,wechat:steven_moda;email:nansun0903@163.com;备注:CSDN。
题目描述
请按下列描达构建一颗二叉树,并返回该树的根节点:
1、先创建值为
-1的根结点,根节点在第0层;2、然后根据
operations依次添加节点:operations[i] = [height, index]表示对第height层的第index个节点node, 添加值为i的子节点:
- 若node 无「左子节点」。则添加左子节点;
- 若node 有「左子节点」但无「右子节点」,则添加右子节点:
- 否则不作任何处理。
height、index 均从
0开始计数;index指所在层的创建顺序。注意:
- 输入用例保证每次操作对应的节点已存在;
- 控制台输出的内容是根据返回的树根节点,按照层序遍历二叉树打印的结果。
示例1
输入:operatio
相关文章:

【华为OD机试真题 Python】创建二叉树
前言:本专栏将持续更新华为OD机试题目,并进行详细的分析与解答,包含完整的代码实现,希望可以帮助到正在努力的你。关于OD机试流程、面经、面试指导等,如有任何疑问,欢迎联系我,wechat:steven_moda;email:nansun0903@163.com;备注:CSDN。 题目描述 请按下列描达构建…...
RuoYi-Vue-Plus搭建(若依)
项目简介 1.RuoYi-Vue-Plus 是重写 RuoYi-Vue 针对 分布式集群 场景全方位升级(不兼容原框架)2.环境安装参考:https://blog.csdn.net/tongxin_tongmeng/article/details/128167926 JDK 11、MySQL 8、Redis 6.X、Maven 3.8.X、Nodejs > 12、Npm 8.X3.IDEA环境配置…...

uboot和linux内核移植流程简述
一、移植uboot流程 1、从半导体芯片厂下载对应的demo,然后编译测试demo版的uboot 开发板基本都是参考半导体厂商的 dmeo 板,而半导体厂商会在他们自己的开发板上移植好 uboot、linux kernel 和 rootfs 等,最终制作好 BSP包提供给用户。我们可…...

【CS224W】(task2)传统图机器学习和特征工程
note 和CS224W课程对应,将图的基本表示写在task1笔记中了;传统图特征工程:将节点、边、图转为d维emb,将emb送入ML模型训练Traditional ML Pipeline Hand-crafted feature ML model Hand-crafted features for graph data Node-l…...
【算法基础】并查集⭐⭐⭐⭐⭐【思路巧,代码短,面试常考】
并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中。其特点是看似并不复杂,但数据量…...

人工智能轨道交通行业周刊-第34期(2023.2.13-2.19)
本期关键词:智慧地铁、枕簧检测选配机器人、智慧工地、接触网检修、工业缺陷检测 1 整理涉及公众号名单 1.1 行业类 RT轨道交通人民铁道世界轨道交通资讯网铁路信号技术交流北京铁路轨道交通网上榜铁路视点ITS World轨道交通联盟VSTR铁路与城市轨道交通RailMetro…...
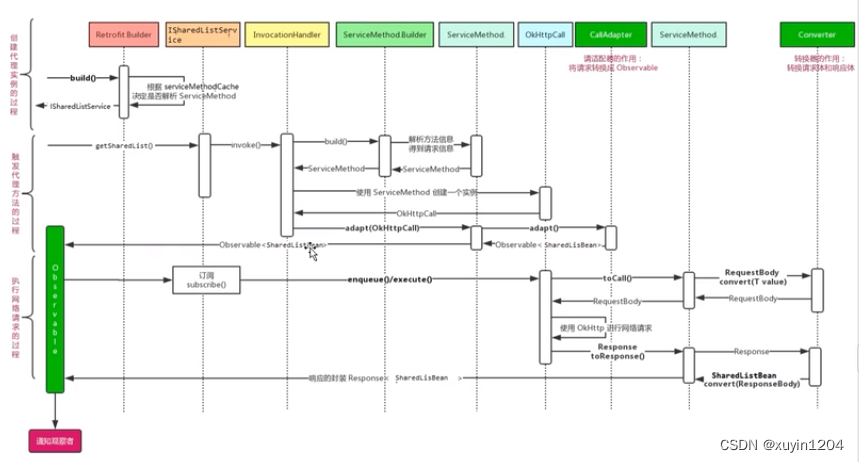
Retrofit 网络框架源码解析(二)
目录一、Okhttp请求二、Retrofit 请求retrofit是如何封装请求的三、Retrofit的构建过程四、Retrofit构建IxxxService对象的过程(Retrofit.create())4.1 动态代理4.2 ServiceMethod4.3 okHttpCall4.4 callAdapter五、Retrofit网络请求操作一、Okhttp请求 …...
SQL Server 2008新特性——更改跟踪
在大型的数据库应用中,经常会遇到部分数据的脱机和多个数据库的合并问题。比如现在有一个全省范围使用的应用程序,每个市都部署了单独的相同的应用程序服务器和数据库服务器,每个月需要将全省所有市的数据全部汇总起来用于出全省的报表&#…...

四六级真题长难句分析与应用
一、基本结构的长难句 基本结构的长难句主要考点:断开和简化 什么是长难句? 其实就是多件事连在了一块,这时候句子就变长、变难了 分析步骤: 第一件事就是要把长难句给断开,把多件事断开成一件一件的事情࿰…...
 | 机试题算法+思路 【2023】)
华为OD机试 - 玩牌高手(Python) | 机试题算法+思路 【2023】
最近更新的博客 华为OD机试 - 寻找路径 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 五键键盘 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - IPv4 地址转换成整数 | 备考思路,刷题要点,答疑 【新解法】 华为OD机试 - 对称美学 | 备考思路,刷题要点,答疑 …...
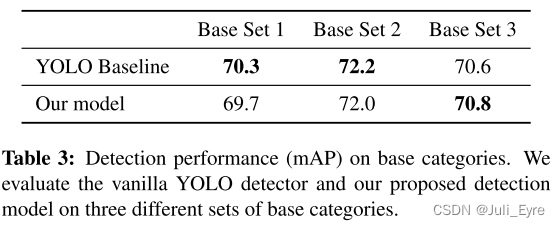
【论文阅读】 Few-shot object detection via Feature Reweighting
Few-shot object detection的开山之作之一 ~~ 特征学习器使用来自具有足够样本的基本类的训练数据来 提取 可推广以检测新对象类的meta features。The reweighting module将新类别中的一些support examples转换为全局向量,该全局向量indicates meta features对于检…...
现代卷积神经网络经典架构图
卷积神经网络(LeNet) LeNet 的简化版深层卷积神经网络(AlexNet) 从LeNet(左)到AlexNet(右)改进: dropOut层 - 不改变期望但是改变方差ReLU层 - 减缓梯度消失MaxPooling数…...
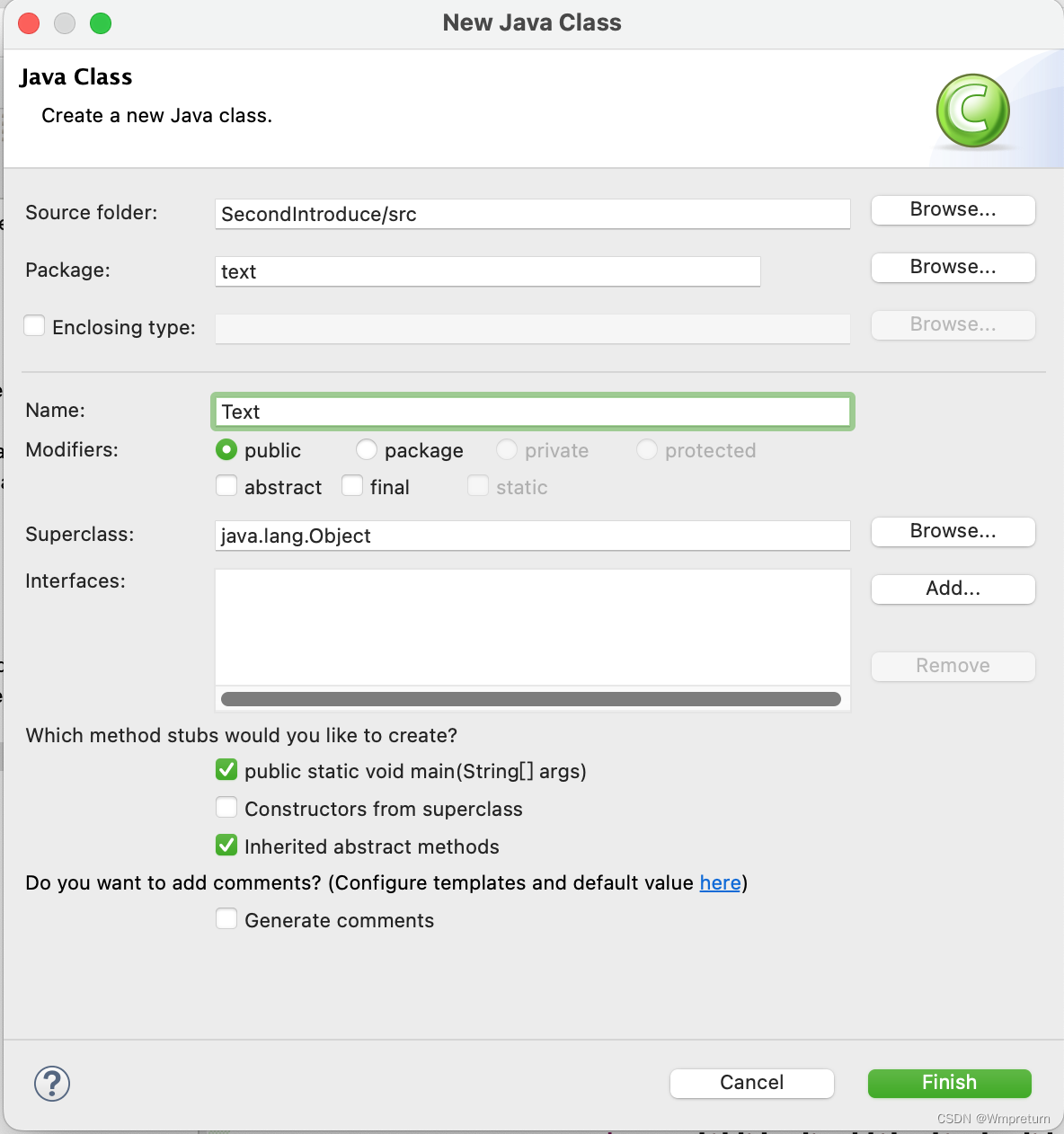
有关eclipse的使用tips
一、alt/键 会产生单词提示,可以提高编程速度。例如不需要辛辛苦苦的打出:System.out.println();整句,只需要在eclipse中输入syso,然后按住ALT/就会出来System.out.println();在alt键/不管用的情况下,可使用以下方法来…...
之CRUD)
Mybatis(4)之CRUD
首先是 增 ,我们要在数据库中增加一个数据 先来看看我们之前的插入语句 <insert id"insertRole">insert into try(id,name,age) values(3,nuonuo,20)</insert> 请注意,我们这里的 insert 是固定的,但在实际的业务场…...

OSG三维渲染引擎编程学习之五十七:“第五章:OSG场景渲染” 之 “5.15 光照”
目录 第五章 OSG场景渲染 5.15 光照 5.15.1 osg::Light光 5.15.2 osg::LightSource光源 第五章 OSG场景渲染 OSG存在场景树和渲染树,“场景数”的构建在第三章“OSG场景组织”已详细阐明,本章开始深入探讨“渲染树”。 渲染树一棵以状态集(StateSet)和渲染叶(RenderLe…...
[教你传话,表白,写信]
第一步 关注飞鸽传话助手 第二部 点击链接进入 第三步 点击发送,输入内容 第四步 就可以收到了...

物联网在智慧农业中的应用
随看现代科技的不断发展,近年来我国农业的进步是显而易见的。从八九十年代农业生产以人力为主,到之后的机械渐渐代替人力,再到如今物联网技术在农业领域的应用,多种前沿技术应用于农业物联网,对智慧农业生产的各个环节…...
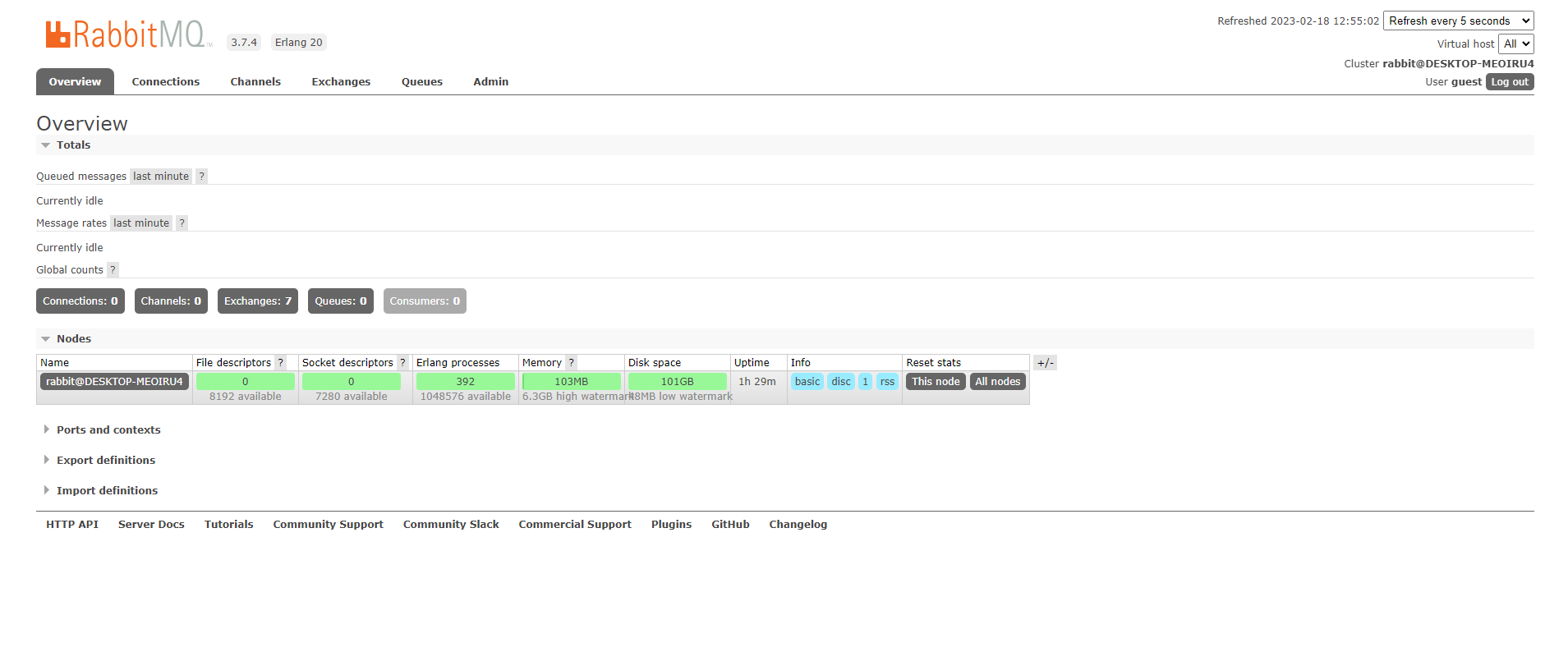
【RabbitMQ】Windows 安装 RabbitMQ
文章目录工具下载Eralng 安装与配置RabbitMQ 安装工具下载 RabbitMQ 3.7.4版本 网盘链接:https://pan.baidu.com/s/1pO6Q8fUbiMrtclpq2KqVVQ?pwdgf29 提取码:gf29 Eralng 网盘链接:https://pan.baidu.com/s/1irf8fgK77k8T9QzsIRwa7g?pwd9…...

MQTT8-MQTT在智能汽车公司的实际应用
一、引言 智能汽车的发展概况 智能汽车作为一种新兴的汽车类型,它的发展历程可以追溯到20世纪90年代。近年来,随着人工智能、物联网、自动驾驶等技术的发展,智能汽车迅速崛起,已经成为汽车行业的一股重要趋势。 智能汽车通过安装传感器、通讯设备和计算设备等,实现了车…...

在elasticsearch8.3中安装elasticsearch-analysis-ik中文分词插件
title: 在elasticsearch8.3中安装elasticsearch-analysis-ik中文分词插件 date: 2022-08-28 00:00:00 tags: ElasticSearchelasticsearch-analysis-ik中文分词插件 categories:ElasticSearch 安装 手动下载 在官方发布页面下载安装包 elasticsearch-analysis-ik-[版本].zip&…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
