Linux:Shell编辑之文本处理器(awk)
目录
绪论
1、用法
1.1 格式选项
1.2 awk 常用内置变量
1.3 awk的打印功能
1.4 奇偶打印
1.5 awk运算
1.6 awk的内置函数:getline
1.7 文本过滤打印
1.8 awk条件判断打印
1.9 三元表达式,类似于java
1.10 awk的精确筛选
1.11 awk和tr比较改变分隔符
1.12 awk结合数组来进行使用
1.13 去重统计
绪论
awk是文本三剑客之一(grep,sed,awk),是功能最强大的文本工具,也是按行来进行操作,对行操作完之后,可以根据指定命令来进行取列
awk的分割符,他的默认分隔符是空格,或者tab键,多个空格,它会自动压缩成一个
1、用法
awk 选项 '模式或者条件{操作}' 文件
1.1 格式选项
-F 指定分割符,如果是空格,则不需要加F
-v 变量赋值
{操作}:默认为打印
eg:awk '{print $1}' test.txt 打印第一列
打印多列的话用逗号隔开,$0表示全部打印
1.2 awk 常用内置变量
$0 打印所有内容
$n 处理行的第几列
NR 处理行的行号
NF 处理当前行的字段个数,$NF就表示最后一个字段
FS 列分割符,指定文本的分割符,和F作用一直
F:分割符 FS=":"
OFS 输出文本的分割符
RS 输出分割符为回车,行分割符
内置变量$n要加$,表示列的;其他的内置变量,不用加$,更不能用引号,也不能用括号,否则会被当成字符串处理
1.3 awk的打印功能
awk '{print} ' 文件名
awk '{print NR} ' 文件名
awk '{print NR,$0} ' 文件名
指定行号打印输出内容:
awk 'NR==3{print}' test,txt 打印第三行
awk 'NR==2,NR==4{print}' test,txt 打印第二到四行
awk 'NR==2;NR==4{print}' test,txt 打印第二和四行
1.4 奇偶打印
awk 'NR%2==0{print}' 文件名 偶数打印
1.5 awk运算
awk 'BEGIN{PRINT 10+20}'
awk 'begin{print 3^2}' 3的2次方,也支持小数运算
awk '{print $3}' test.txt取出第三行
1.6 awk的内置函数:getline
· 如果getline左右两侧没有重定向符号(<>),或者没有(|)时,awk会先读第一行,但是如果加了getline,跳过第一行,读取第二行
awk '{getline;print}' test.txt 打印了第二行和第四行,偶数打印
awk '{print;getline}' test.txt 奇数打印
· 如果两边有重定向或者管道符,getline作用于定向输入文件
awk '{getline < "test1.txt";print>"test2.txt"}' test1.txt操作对象是test1.TXT,获取test1的内容,传给test2
ls | awk '{getline ky30;print ,ky30;}' getline:自定义的变量。把ls输出的结果传给ky30,打印前面ls的结果
1.7 文本过滤打印
awk 以root为开头的行:
awk '/^root/{print}' /etc/passwd
awk 'BEGIN{..};{..};END{..}' 文件在对文件进行操作之前会先执行BEGIN{..}的模式条件,或者是命令操作。中间的{..}是真正的处理文件的命令。END{..}结束语句,一般都是打印执行结果
v变量赋值,指的是改变分割符
1.8 awk条件判断打印
awk -F: '$3>100{print}' /etc/passwd | head -n 15 第三列大于100的打印出来
取反:awk -F: '!($3>10){print}' /etc/passwd | head -n 15
awk支持条件判断语句if
awk -F: '{if ($3>10) {print}}' /etc/passwd
1.9 三元表达式,类似于java
格式:awk '(条件表达式)?(A表达式或者值):(B的表达式或者值)'
?相当于if :相当于else
awk -F: '{i=($3>$4)?$3:$4;{print $1,$2}}' /etc/passwd
1.10 awk的精确筛选

$NF:最后一个字段
head -n 2 /etc/passwd | awk -F: '{print $NF}' 第七个字段为bash,打印第一列和最后一列
awk -F: '$7!~"nologin"{print $1,$3}' /etc/passwd 第七个字段不是nologin的打印第一列和第三列
&&和 ||或 条件表达式用括号括起来
1.11 awk和tr比较改变分隔符
echo a b < d | tr " " " " ":" 输出a:b:c:d
1.12 awk结合数组来进行使用
在awk中怎么定义数组

1.13 去重统计


提取host.txt主机名

awk -F '[ .]+' '{print $2}' test.txt
相关文章:

Linux:Shell编辑之文本处理器(awk)
目录 绪论 1、用法 1.1 格式选项 1.2 awk 常用内置变量 1.3 awk的打印功能 1.4 奇偶打印 1.5 awk运算 1.6 awk的内置函数:getline 1.7 文本过滤打印 1.8 awk条件判断打印 1.9 三元表达式,类似于java 1.10 awk的精确筛选 1.11 awk和tr比较改变…...
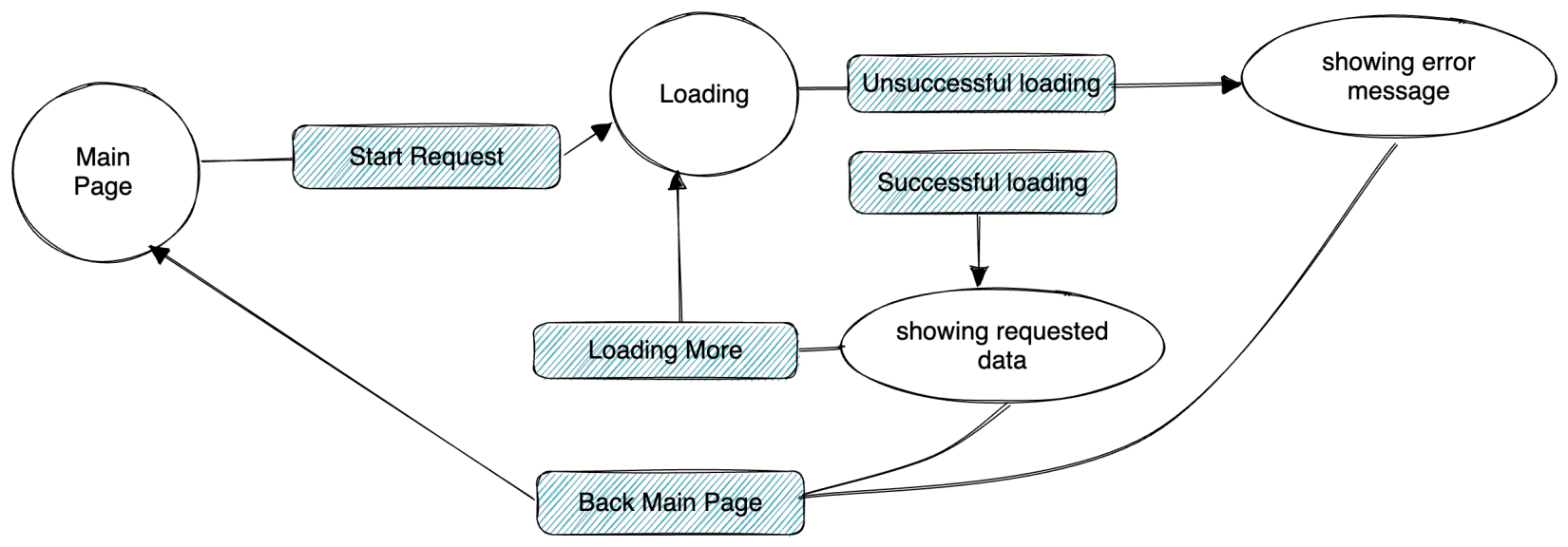
探索FSM (有限状态机)应用
有限状态机(FSM) 是计算机科学中的一种数学模型,可用于表示和控制系统的行为。它由一组状态以及定义在这些状态上的转换函数组成。FSM 被广泛用于计算机程序中的状态机制。 有限状态机(FSM)应用场景 在各种自动化系统…...

6.continue break
6.1continue 关键字 continue 关键字用于立即跳出本次循环,继续下一次循环(本次循环体continue之后的代码会少执行一次)。 例如:吃5个包子,第3个有虫子,就扔掉第3个包子,继续吃第4个第5个包子…...

如何在Linux中强制关闭卡住的PyCharm
在使用PyCharm进行Python开发时,有时可能会遇到卡顿或无响应的情况。当PyCharm卡住时,我们需要强制关闭它以恢复正常操作。今天,我们将介绍在Linux系统中如何强制关闭PyCharm的几种方法。 1. 使用键盘快捷键 在PyCharm所在的窗口中…...

c# Excel数据的导出与导入
搬运:Datagrideview 数据导出Excel , Exel数据导入 //------------------------------------------------------------------------------------- // All Rights Reserved , Copyright (C) 2013 , DZD , Ltd . //----------------------------------------------------------…...

Kotlin~Mediator中介者模式
概念 创建一个中介来降低对象之间的耦合度,关系”多对多“变为“一对多”。 角色介绍 Mediator:抽象中介者,接口或者抽象类。ConcreteMediator:中介者具体实现,实现中介者接口,定义一个List管理Colleagu…...

石子合并问题
一.试题 在一个园形操场的四周摆放N堆石子(N≤100),现要将石子有次序地合并成一堆。规定 每次只能选相邻的两堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。 编一程序,由文件读入…...

剑指Offer-搜索与回溯算法
文章目录 剑指 Offer 32 - I. 从上到下打印二叉树题意:解:代码: 剑指 Offer 32 - II. 从上到下打印二叉树 II题意:解:代码: 剑指 Offer 32 - III. 从上到下打印二叉树 III题意:解:代…...

【云原生】Docker 详解(三):Docker 镜像管理基础
Docker 详解(三):Docker 镜像管理基础 1.镜像的概念 镜像可以理解为应用程序的集装箱,而 Docker 用来装卸集装箱。 Docker 镜像含有启动容器所需要的文件系统及其内容,因此,其用于创建并启动容器。 Dock…...
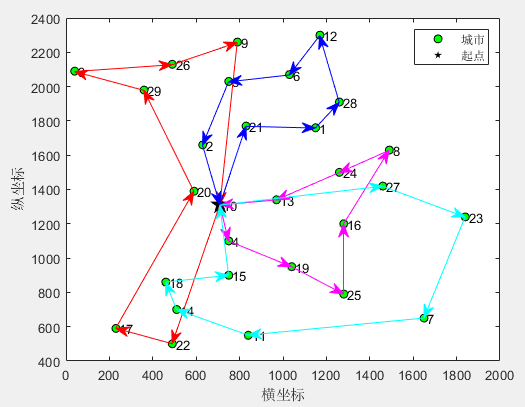
SD-MTSP:蜘蛛蜂优化算法SWO求解单仓库多旅行商问题MATLAB(可更改数据集,旅行商的数量和起点)
一、蜘蛛蜂优化算法SWO 蜘蛛蜂优化算法(Spider wasp optimizer,SWO)由Mohamed Abdel-Basset等人于2023年提出,该算法模型雌性蜘蛛蜂的狩猎、筑巢和交配行为,具有搜索速度快,求解精度高的优势。蜘蛛蜂优化算…...
) 使用】)
【ARM 嵌入式 编译系列 3.1 -- GCC __attribute__((used)) 使用】
文章目录 __attribute__((used)) 属性介绍代码演示编译与输出GCC 编译选项 上篇文章:ARM 嵌入式 编译系列 3 – GCC attribute((weak)) 弱符号使用 下篇文章:ARM 嵌入式 编译系列 3.2 – glibc 学习 __attribute__((used)) 属性介绍 在普通的 C/C 程序中…...
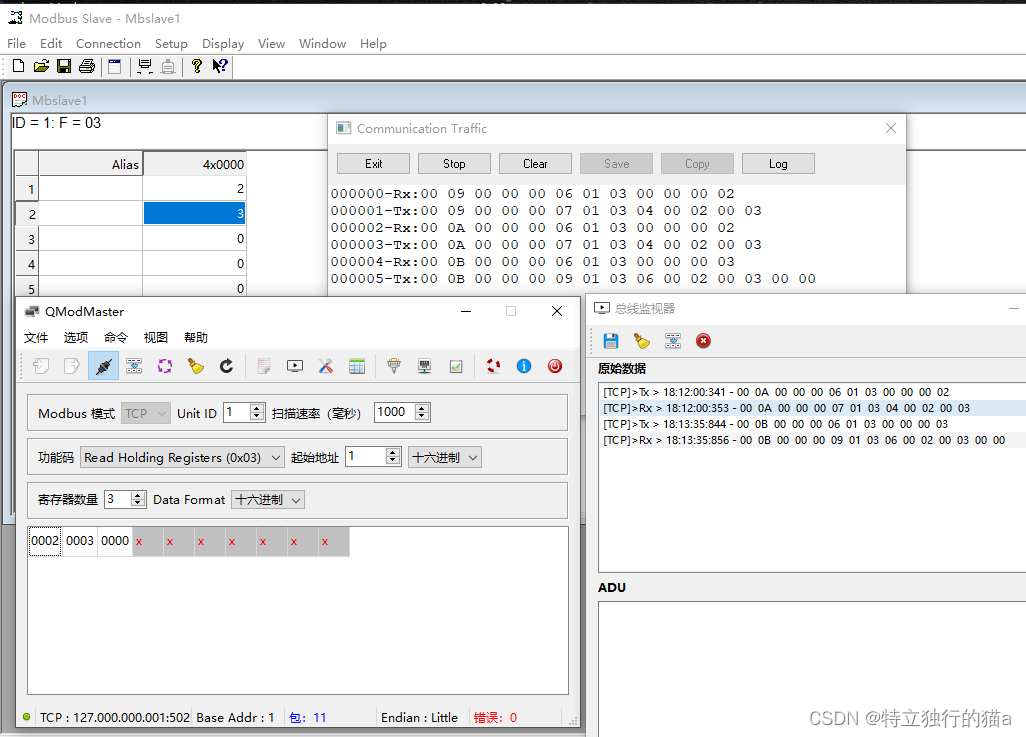
C++ ModBUS TCP客户端工具 qModMaster 介绍及使用
qModMaster工具介绍 QModMaster是一个基于Qt的Modbus主站(Master)模拟器,用于模拟和测试Modbus TCP和RTU通信。它提供了一个直观的图形界面,使用户能够轻松设置和发送Modbus请求,并查看和分析响应数据。 以下是QModM…...
笔记本电脑如何把sd卡数据恢复
在使用笔记本电脑过程中,如果不小心将SD卡里面的重要数据弄丢怎么办呢?别着急,本文将向您介绍SD卡数据丢失常见原因和恢复方法。 ▌一、SD卡数据丢失常见原因 - 意外删除:误操作或不小心将文件或文件夹删除。 - 误格式化&#…...

【2023 华数杯全国大学生数学建模竞赛】 B题 不透明制品最优配色方案设计 39页论文及python代码
【2023 华数杯全国大学生数学建模竞赛】 B题 不透明制品最优配色方案设计 39页论文及python代码 1 题目 B 题 不透明制品最优配色方案设计 日常生活中五彩缤纷的不透明有色制品是由着色剂染色而成。因此,不透明制品的配色对其外观美观度和市场竞争力起着重要作用。…...
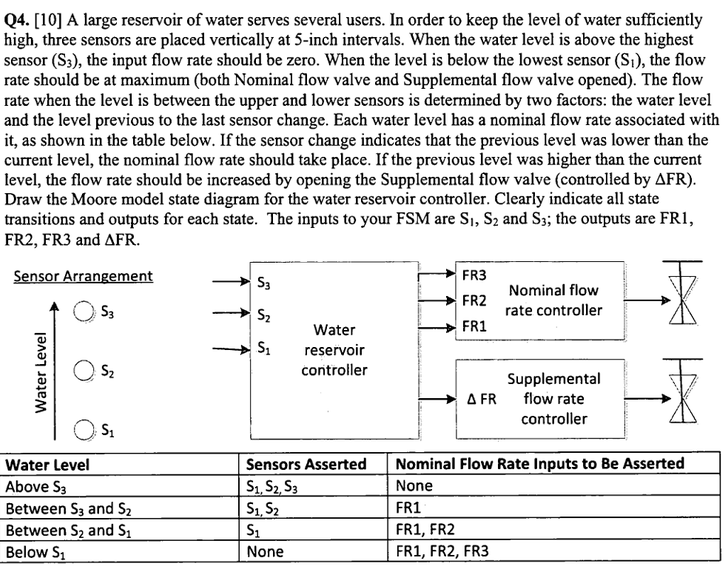
Exams/ece241 2013 q4
蓄水池问题 S3 S2 S1 例如:000 代表 无水 ,需要使FR3, FR2, FR1 都打开(111) S3 S2 S1 FR3 FR2 FR1 000 111 001 011 011 001 111 000 fr代表水变深为…...
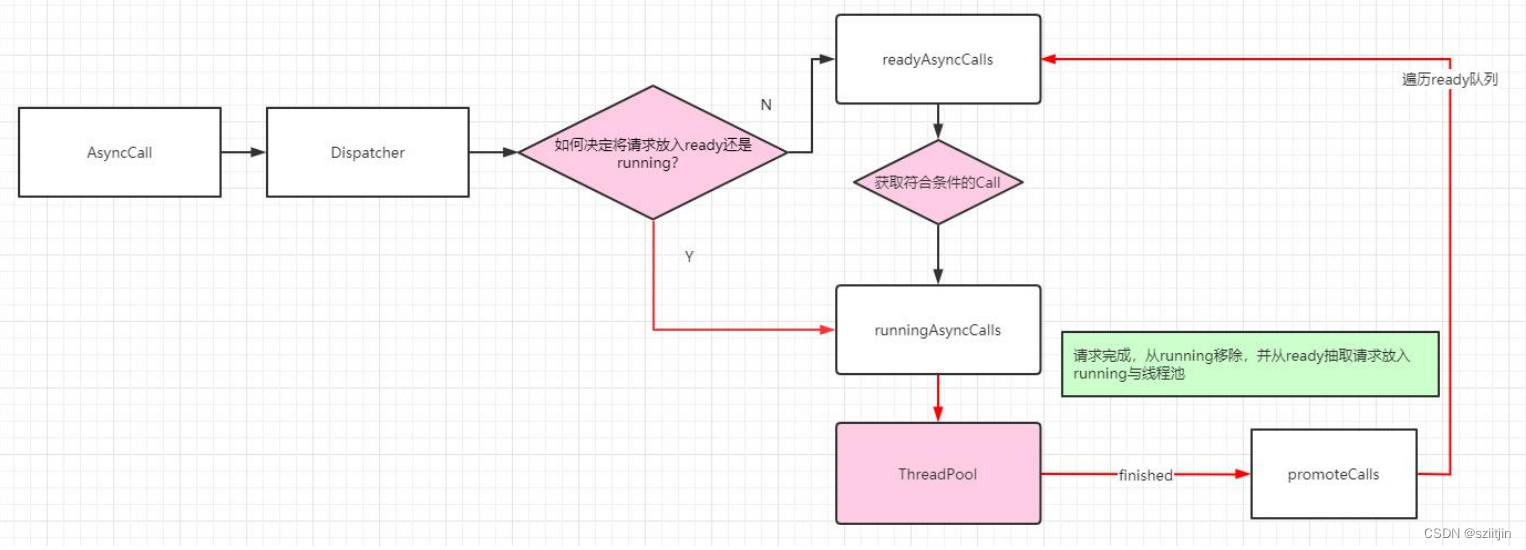
Android OkHttp源码分析--分发器
OkHttp是当下Android使用最频繁的网络请求框架,由Square公司开源。Google在Android4.4以后开始将源码中 的HttpURLConnection底层实现替换为OKHttp,同时现在流行的Retrofit框架底层同样是使用OKHttp的。 OKHttp优点: 1、支持Http1、Http2、Quic以及Web…...
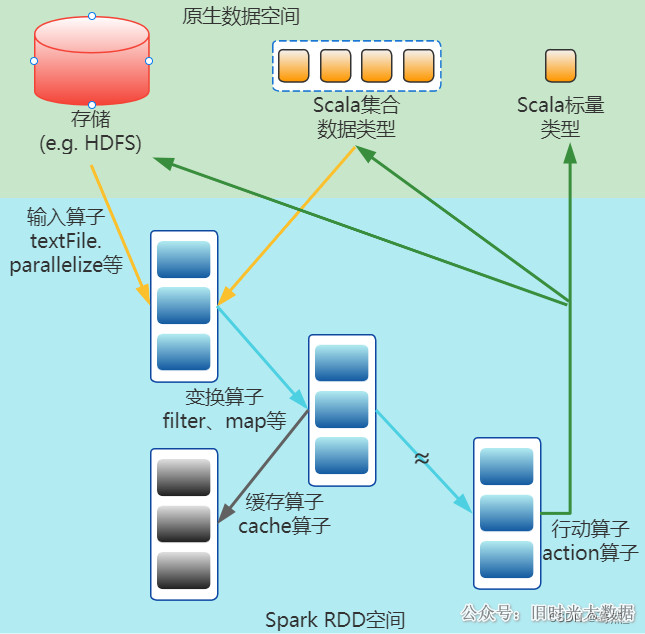
大数据面试题:说下Spark中的Transform和Action,为什么Spark要把操作分为Transform和Action?
面试题来源: 《大数据面试题 V4.0》 大数据面试题V3.0,523道题,679页,46w字 可回答:Spark常见的算子介绍一下 参考答案: 我们先来看下Spark算子的作用: 下图描述了Spark在运行转换中通过算…...
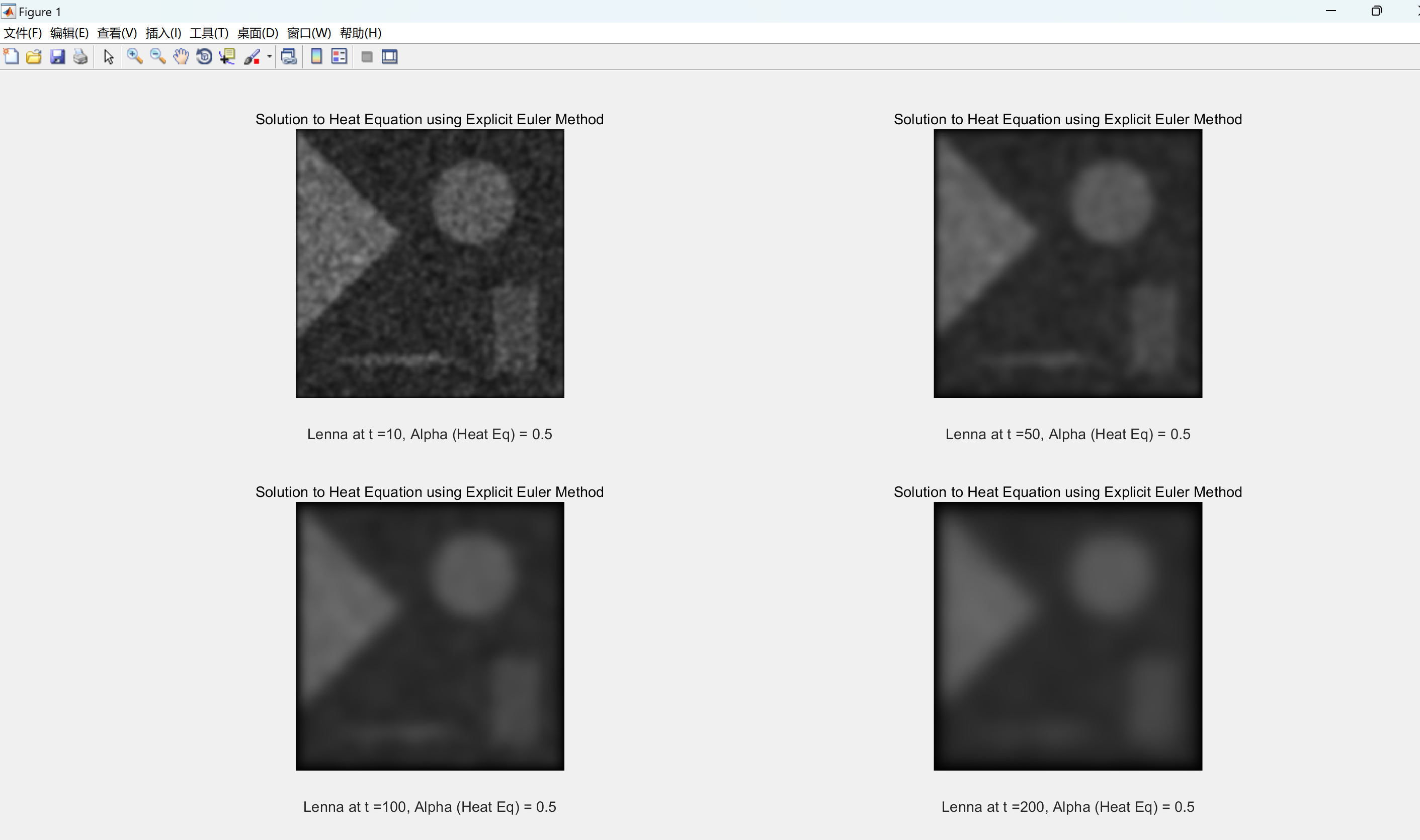
【图像去噪的扩散滤波】基于线性扩散滤波、边缘增强线性和非线性各向异性滤波的图像去噪研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
)
python函数、运算符等简单介绍2(无顺序)
list(列表) 列表是Python的一种内置数据类型,列表是可以装各种数据类 型的容器 # 第一种list创建方式 list_name [晓东,小刚,明明,小红,123,123.4,123] print(list_name) print(type(list_name)) # 输出结果: [晓东, 小刚, 明明…...

k8s 自身原理 3
前面有分享到 master 主节点上的 四个组件,etcd,ApiServer,scheduler,controller manager 接下来我们分享一波 woker 节点上的组件,xdm 还记得 worker 节点上都有什么吗? kubeletkube-proxy实际的服务对应…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...
