AtCoder Beginner Contest 313D题题解
文章目录
- [ Odd or Even](https://atcoder.jp/contests/abc313/tasks/abc313_d)
- 问题建模
- 问题分析
- 1.分析每次查询的作用
- 2.利用异或运算的性质设计查询方法
Odd or Even


问题建模
有n个数,每个数为0或者1,最多可以进行n次询问,每次询问选择k个不同的数,每次询问会得到这些数相加的奇偶性,问这n个数的值分别为多少。
问题分析
1.分析每次查询的作用
每次查询,可以获得这些数相加的奇偶性,即0或者1,则等价于将这些数进行异或得到的异或值。
2.利用异或运算的性质设计查询方法
异或运算有一个性质,就是一个数异或上另一个数偶数次,等价于没有异或该数。所以我们可以构造一种查询方法,其中某一个数被异或奇数次,而剩余数被异或上偶数次,从而得到该数的值。
则可以先进行k+1次查询,每次查询缺少k+1个数中的一个,这样k+1次查询得到的异或值,为k+1个元素每个元素出现奇数次的总异或值,那对于该值异或上前k+1次查询单次得到的异或值,等价于缺少值出现奇数次,其余值出现偶数次,则可以得到缺少值的数值。
然后对于剩下的元素,查询只需要前k-1个数再带一个数的异或值,然后与前k个数的异或值进行比较,若相同,则说明当前元素值与第k个元素相同,否则不同。
#include<bits/stdc++.h>#define x first
#define y second
#define C(i) str[0][i]!=str[1][i]
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
const int N =1100, Mod =998244353;
int a[N];
int s[N];
int n,k;void get_k(){///获得前k+1个数每个数出现奇数次的总异或值int res=0;for(int i=1;i<=k+1;i++){cout <<"? ";for(int j=1;j<=k+1;j++){if(j!=i) cout <<j <<" ";}cout<<endl;cin >>s[i];res^=s[i];}///用总异或值,异或是上缺少某一个值的异或值,从而得到对应为的值for(int i=1;i<=k+1;i++){a[i]=res^s[i];}
}void solve() {cin >>n >>k;get_k();///用前k个数的异或值与后面仅有第k个数不同的异或值作比较,从而得到对应位置的值for(int i=k+2;i<=n;i++){cout <<"? " <<i <<" ";for(int j=1;j<=k-1;j++){cout <<j <<" ";}cout <<endl;cin >>s[i];if(s[i]==s[k+1]) a[i]=a[k];else a[i]=a[k]^1;}cout <<"! ";for(int i=1;i<=n;i++){cout <<a[i] <<" ";}cout <<endl;
} int main() {int t = 1;//cin >> t;while (t--) solve();return 0;
}
相关文章:

AtCoder Beginner Contest 313D题题解
文章目录 [ Odd or Even](https://atcoder.jp/contests/abc313/tasks/abc313_d)问题建模问题分析1.分析每次查询的作用2.利用异或运算的性质设计查询方法 Odd or Even 问题建模 有n个数,每个数为0或者1,最多可以进行n次询问,每次询问选择k个…...

mybatis 中的<![CDATA[ ]]>用法及说明
<![CDATA[ ]]>作用 <![CDATA[ ]]> 在mybatis、ibatis等书写SQL的xml中比较常见,是一种XML语法,他的作用是 可以忽略xml的转义(在该标签中的语句和字符原本是什么样的,在拼接成SQL后还是什么样的) 使用&a…...

从零学算法34
34.给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。 如果数组中不存在目标值 target,返回 [-1, -1]。 你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。 示例 1࿱…...
qiankun-微前端--vue2
项目结构 主应用技术: vue2 子应用技术:vue2 项目目录 这里是特意将主子项目分开来的,方便管理 主应用 安装 qiankun npm install qiankun重新定义一个启动端口,防止和其它子应用共用同一个端口(vue.config.js&…...
Win7累积补丁更新包_UpdatePack7R2-23.8.10
UpdatePack7是最新的Win7补丁累积更新包,Windows 7更新补丁安装包,Win7累积更新离线安装包包括所有关键更新和安全更新及Internet Explorer所有版本的更新,此外还集成了NVMe驱动和USB3.0驱动,使用它还可以将累积更新封装到系统内&…...
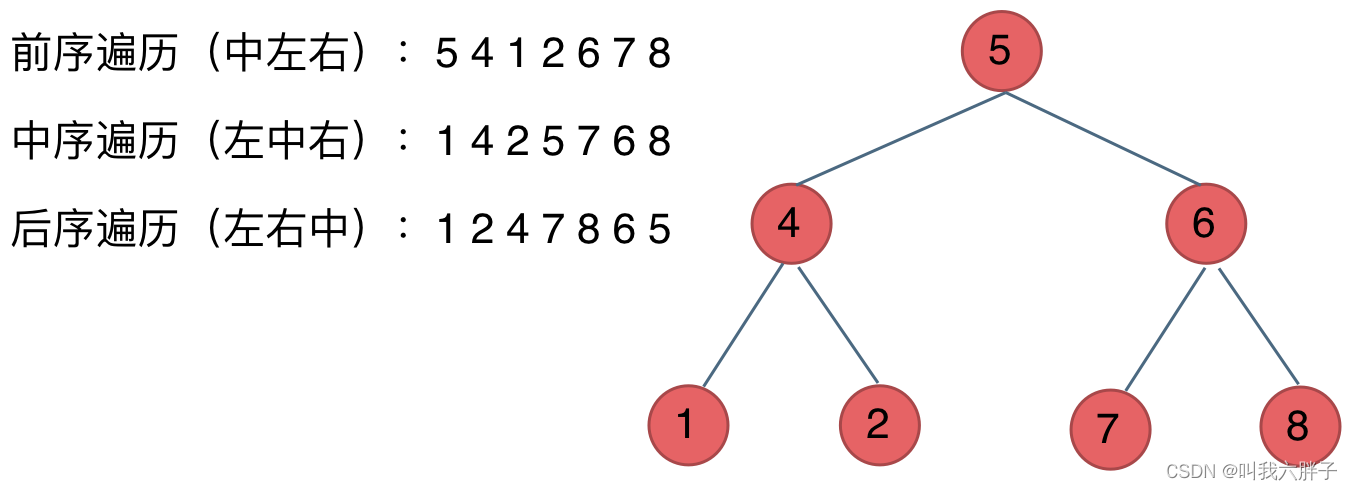
【二叉树】1-5,理论基础、前中后序遍历的递归法和迭代法、层序遍历
理论基础、前中后序遍历的递归法和迭代法、层序遍历 1,二叉树的种类满二叉树完全二叉树二叉搜索树平衡二叉搜索树 2,存储方式链式存储线式存储 3,二叉树的遍历深度优先搜索前序遍历(递归法、迭代法)中序遍历࿰…...

Mybatis-plus动态条件查询QueryWrapper的使用
Mybatis-plus动态条件查询QueryWrapper的使用 一:queryWrapper介绍 queryWrapper是mybatis plus中实现查询的对象封装操作类,可以封装sql对象,包括where条件,order by排序,select哪些字段等等,他的层级关…...
Redis安装配置远程连接
1. yum 安装 redis: 直接使用命令,将 redis 安装到 linux 服务器中: yum -y install redis 2. 启动 redis: 在 xshell 里,可以使用下面命令,以后台方式启动 redis: [rootVM-8-17-centos /]…...
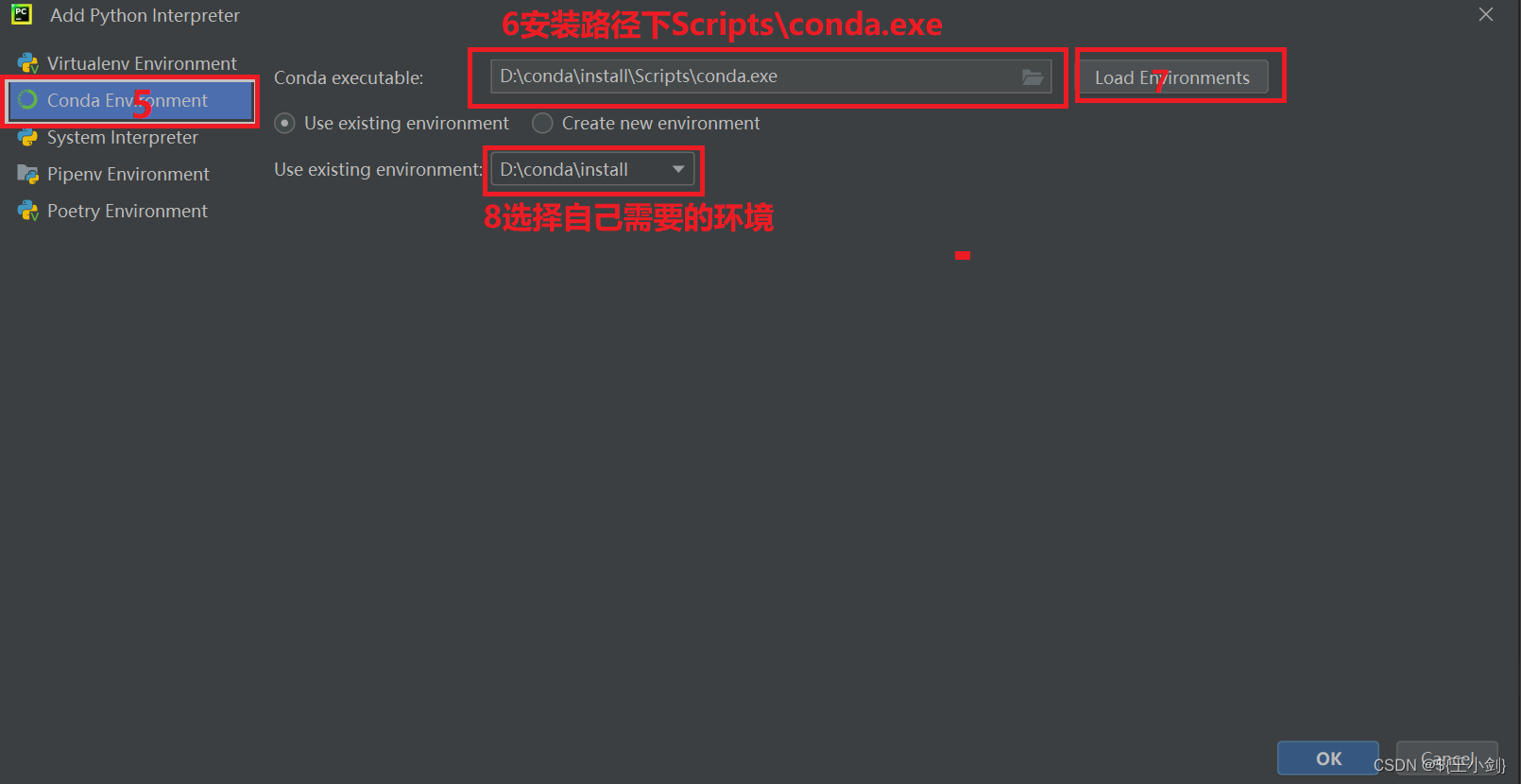
pycharm中配置conda
安装好pycharm和conda后,打开pycharm:...
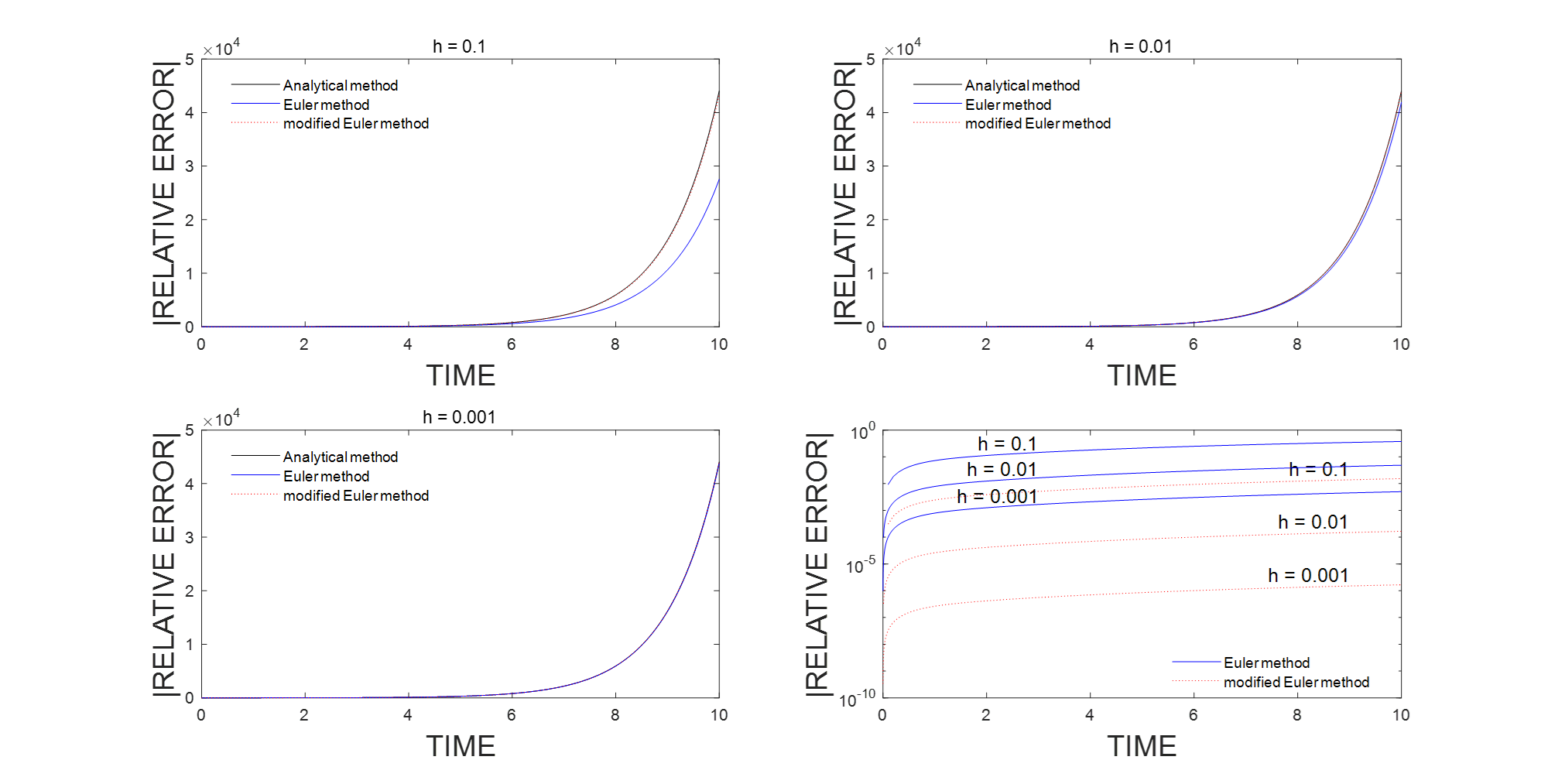
matlab解常微分方程常用数值解法1:前向欧拉法和改进的欧拉法
总结和记录一下matlab求解常微分方程常用的数值解法,本文先从欧拉法和改进的欧拉法讲起。 d x d t f ( x , t ) , x ( t 0 ) x 0 \frac{d x}{d t}f(x, t), \quad x\left(t_{0}\right)x_{0} dtdxf(x,t),x(t0)x0 1. 前向欧拉法 前向欧拉法使用了泰勒展开的第…...
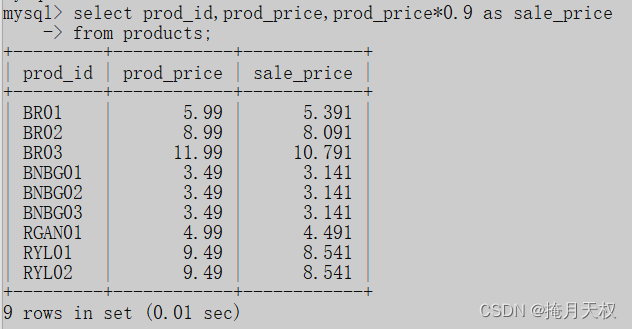
SQL | 计算字段
7-创建计算字段 7.1-计算字段 存储在数据库中的数据一般不是我们所需要的字段格式, 需要公司名称,同时也需要公司地址,但是这两个数据存储在不同的列中。 省,市,县和邮政编码存储在不同的列中,但是当我们…...

leetcode做题笔记67
给你两个二进制字符串 a 和 b ,以二进制字符串的形式返回它们的和。 思路一:模拟题意 void reserve(char* s) {int len strlen(s);for (int i 0; i < len / 2; i) {char t s[i];s[i] s[len - i - 1], s[len - i - 1] t;} }char* addBinary(cha…...
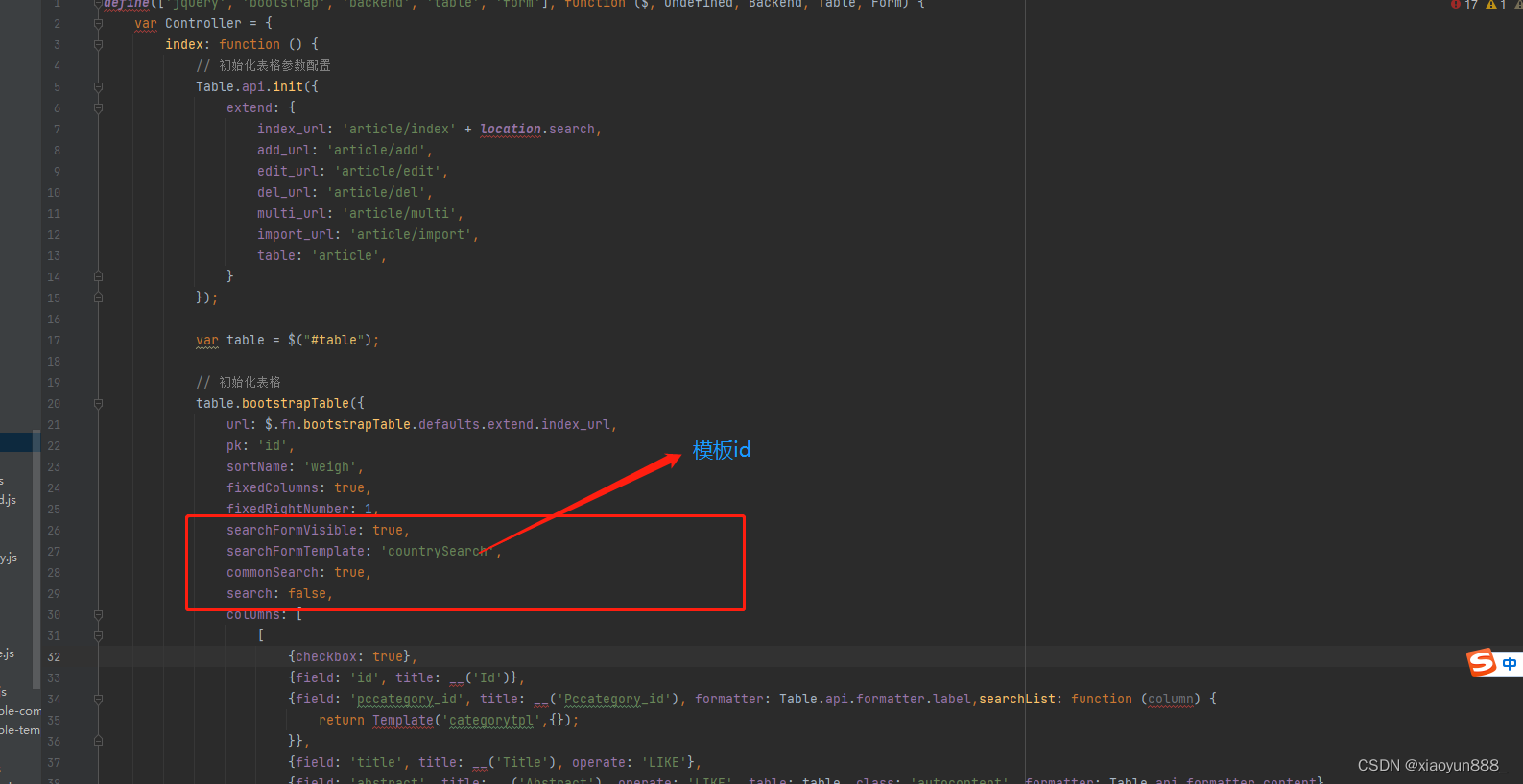
fastadmin 自定义搜索分类和时间范围
1.分类搜索,分类信息获取----php 2.对应html页面,页面底部加搜索提交代码(这里需要注意:红框内容) 图上代码----方便直接复制使用 <script id"countrySearch" type"text/html"><!--form…...

Oracle Data Redaction与Data Pump
如果表定义了Redaction Policy,导出时数据会脱敏吗?本文解答这个问题。 按照Oracle文档Advanced Security Guide第13章,13.6.5的Tutorial,假设表HR.jobs定义了Redaction Policy。 假设HR用户被授予了访问目录对象的权限…...

设计模式(6)原型模式
一、介绍 Java中自带的原型模式是clone()方法。该方法是Object的方法,native类型。他的作用就是将对象的在内存的那一块内存数据一字不差地再复制一个。我们写简单类的时候只需要实现Cloneable接口,然后调用Object::clone方法就可实现克隆功能。这样实现…...

pywinauto结合selenium实现文件上传
简介 PC端-Windows上的元素识别可用viewWizard工具 PC端-Windows上的元素操作可用pywinauto库 浏览器上网页的元素识别可用selenium 安装 pip installer pywinauto 使用须知 pywinauto官方文档 确定app的可访问技术 1、win32 API(backend=“win32”) 一般是MFC、VB6、VC…...
【Java多线程学习7】Java线程池技术
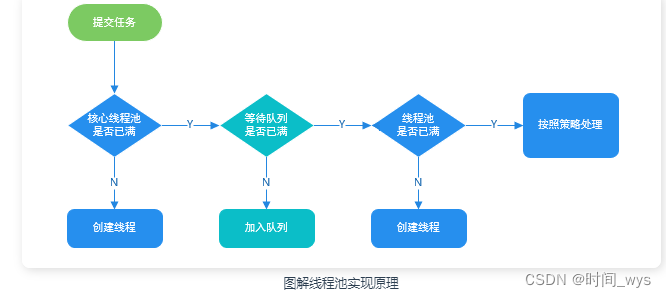
线程池技术 一、什么是线程池 线程池顾名思义是管理一组线程的池子。当有任务要处理时,直接从线程池中获取线程来处理,处理完之后线程不会立即销毁,而是等待下一个任务。 二、为什么要使用线程池? 线程池的作用? 1、降低资源…...
VMware虚拟机NAT模式Ubuntu无法上网解决方案
发现只要NAT模式,ping地址时就报网络不可达,且右上方网络图标消失,但是外部USB网络设备又只能在NAT模式下使用。。。 博主的解决方案如下: 按WinR键入services.msc, 找到VMware DHCP Service、VMware NAT Service和V…...

Linux中无法忘记mysql密码处理办法
找到/etc/my.cnf或者/etc/mysql/my.cnf文件 添加下面两行代码,取消密码验证 [mysqld] skip-grant-table使用命令登录:mysql -u root -p,回车,回车使用sql语句来修改密码 mysql>use mysql; mysql>update user set password…...
)
vue 使用 el-upload 上传文件(自动上传/手动上传)
vue 使用 el-upload 上传文件(自动上传/手动上传) 文章目录 1. 自动上传(选择完文件后,调用axios上传)2.手动上传 1. 自动上传(选择完文件后,调用axios上传) <el-uploadref"upload1"action:multiple"false"accept".xlsx,.csv,.xls":auto-upl…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
