【深度学习所有损失函数】在 NumPy、TensorFlow 和 PyTorch 中实现(2/2)
一、说明
在本文中,讨论了深度学习中使用的所有常见损失函数,并在NumPy,PyTorch和TensorFlow中实现了它们。
(二-五)见
六、稀疏分类交叉熵损失
稀疏分类交叉熵损失类似于分类交叉熵损失,但在真实标签作为整数而不是独热编码提供时使用。它通常用作多类分类问题中的损失函数。
稀疏分类交叉熵损失的公式为:
L = -1/N * sum(log(Y_hat_i)) 其中 是每个样本的真实类标签的预测概率,是样本数。Y_hat_iiN
换句话说,该公式计算每个样本的真实类标签的预测概率的负对数,然后对所有样本的这些值求平均值。
与对真实标签使用独热编码的分类交叉熵损失不同,稀疏分类交叉熵损失直接使用整数标签。每个样本的真实标签表示为 0 到 之间的单个整数值,其中 是类的数量。iC-1C
6.1 在 NumPy 中的实现
import numpy as npdef sparse_categorical_crossentropy(y_true, y_pred):# convert true labels to one-hot encodingy_true_onehot = np.zeros_like(y_pred)y_true_onehot[np.arange(len(y_true)), y_true] = 1# calculate lossloss = -np.mean(np.sum(y_true_onehot * np.log(y_pred), axis=-1))return loss 在此实现中, 是整数标签数组,是每个样本的预测概率数组。该函数首先使用 NumPy 的高级索引功能将真实标签转换为独热编码格式,以创建一个形状数组,其中是样本数和类数,每行对应于单个样本的真实标签分布。y_truey_pred(N, C)NC
然后,该函数使用上一个答案中描述的公式计算损失:。这是使用 NumPy 的广播实现的,其中创建一个形状数组,其中每个元素表示 和 中相应元素的乘积。然后,该函数用于对维度求和,并用于对维度求平均值。-1/N * sum(log(Y_hat_i))y_true_onehot * np.log(y_pred)(N, C)y_true_onehotnp.log(y_pred)sumCmeanN
下面是如何使用该函数的示例:
# define true labels as integers and predicted probabilities as an array
y_true = np.array([1, 2, 0])
y_pred = np.array([[0.1, 0.8, 0.1], [0.3, 0.2, 0.5], [0.4, 0.3, 0.3]])# calculate the loss
loss = sparse_categorical_crossentropy(y_true, y_pred)# print the loss
print(loss)这将输出给定输入的稀疏分类交叉熵损失的值。
6.2 TensorFlow 中的实现
import tensorflow as tfdef sparse_categorical_crossentropy(y_true, y_pred):loss = tf.keras.losses.sparse_categorical_crossentropy(y_true, y_pred, from_logits=False)return loss# define true labels as integers and predicted probabilities as a tensor
y_true = tf.constant([1, 2, 0])
y_pred = tf.constant([[0.1, 0.8, 0.1], [0.3, 0.2, 0.5], [0.4, 0.3, 0.3]])# calculate the loss
loss = sparse_categorical_crossentropy(y_true, y_pred)# print the loss
print(loss.numpy())在此实现中, 是整数标签数组,是每个样本的预测概率数组。该函数使用 TensorFlow 提供的函数来计算损失。设置该参数以确保 表示概率而不是对数值。y_truey_predtf.keras.losses.sparse_categorical_crossentropyfrom_logitsFalsey_pred
6.3 在 PyTorch 中的实现
import torch.nn.functional as F
import torchdef sparse_categorical_crossentropy(y_true, y_pred):loss = F.cross_entropy(y_pred, y_true)return loss# define true labels as integers and predicted logits as a tensor
y_true = torch.tensor([1, 2, 0])
y_pred = torch.tensor([[0.1, 0.8, 0.1], [0.3, 0.2, 0.5], [0.4, 0.3, 0.3]])# calculate the loss
loss = sparse_categorical_crossentropy(y_true, y_pred)# print the loss
print(loss.item()) 在此实现中, 是一个整数标签数组,并且是每个样本的预测对数数组。该函数使用 PyTorch 的函数来计算损失。张量应该具有形状,其中是样本的数量,是类的数量。y_truey_predF.cross_entropyy_pred(N, C)NC
七、骰子损失
骰子损失,也称为索伦森-骰子系数或 F1 分数,是图像分割任务中使用的损失函数,用于测量预测分割与地面实况之间的重叠。骰子损失范围从 0 到 1,其中 0 表示没有重叠,1 表示完全重叠。
骰子损失定义为:
Dice Loss = 1 - (2 * intersection + smooth) / (sum of squares of prediction + sum of squares of ground truth + smooth) 其中 是预测和地面真实掩码的元素乘积,是一个平滑常数(通常是一个较小的值,例如 1e-5),以防止除以零,并且总和将覆盖掩码的所有元素。intersectionsmooth
骰子损失可以在各种深度学习框架中实现,如TensorFlow,PyTorch和NumPy。该实现涉及使用框架中可用的逐元素乘积和求和运算计算交集和平方和。
7.1 在 NumPy 中的实现
import numpy as npdef dice_loss(y_true, y_pred, smooth=1e-5):intersection = np.sum(y_true * y_pred, axis=(1,2,3))sum_of_squares_pred = np.sum(np.square(y_pred), axis=(1,2,3))sum_of_squares_true = np.sum(np.square(y_true), axis=(1,2,3))dice = 1 - (2 * intersection + smooth) / (sum_of_squares_pred + sum_of_squares_true + smooth)return dice 在此实现中,分别是基本事实和预测掩码。该参数用于防止被零除。和函数分别用于计算交集和平方和。最后,使用上一个答案中描述的公式计算骰子损失。y_truey_predsmoothsumsquare
请注意,此实现假定 和 是具有维度的 4D 数组。如果您的掩码具有不同的形状,则可能需要相应地修改实现。y_truey_pred(batch_size, height, width, num_classes)
7.2 TensorFlow 中的实现
import tensorflow as tfdef dice_loss(y_true, y_pred, smooth=1e-5):intersection = tf.reduce_sum(y_true * y_pred, axis=(1,2,3))sum_of_squares_pred = tf.reduce_sum(tf.square(y_pred), axis=(1,2,3))sum_of_squares_true = tf.reduce_sum(tf.square(y_true), axis=(1,2,3))dice = 1 - (2 * intersection + smooth) / (sum_of_squares_pred + sum_of_squares_true + smooth)return dice 在此实现中,和 是 TensorFlow 张量分别表示地面真相和预测掩码。该参数用于防止被零除。和函数分别用于计算交集和平方和。最后,使用上一个答案中描述的公式计算骰子损失。y_truey_predsmoothreduce_sumsquare
请注意,此实现假定 和 是具有维度的 4D 张量。如果您的掩码具有不同的形状,则可能需要相应地修改实现。y_truey_pred(batch_size, height, width, num_classes)
7.3 在 PyTorch 中的实现
import torchdef dice_loss(y_true, y_pred, smooth=1e-5):intersection = torch.sum(y_true * y_pred, dim=(1,2,3))sum_of_squares_pred = torch.sum(torch.square(y_pred), dim=(1,2,3))sum_of_squares_true = torch.sum(torch.square(y_true), dim=(1,2,3))dice = 1 - (2 * intersection + smooth) / (sum_of_squares_pred + sum_of_squares_true + smooth)return dice 在此实现中,和 是 PyTorch 张量分别表示基本事实和预测掩码。该参数用于防止被零除。和函数分别用于计算交集和平方和。最后,使用上一个答案中描述的公式计算骰子损失。y_truey_predsmoothsumsquare
请注意,此实现假定 和 是具有维度的 4D 张量。如果您的掩码具有不同的形状,则可能需要相应地修改实现。y_truey_pred(batch_size, num_classes, height, width)
八、KL散度损失
KL(Kullback-Leibler)散度损失是两个概率分布彼此差异程度的度量。在机器学习的上下文中,它通常用作损失函数来训练从给定分布生成新样本的模型。
两个概率分布 p 和 q 之间的 KL 散度定义为:
KL(p||q) = sum(p(x) * log(p(x) / q(x)))
在机器学习的上下文中,p 表示真实分布,q 表示预测分布。KL 散度损失衡量预测分布与真实分布的匹配程度。
KL 散度损失可用于各种任务,例如图像生成、文本生成和强化学习。但是,由于它具有非凸形式,因此可能很难优化。
在实践中,KL散度损失通常与其他损失函数(如交叉熵损失)结合使用。通过将KL散度损失添加到交叉熵损失中,鼓励模型生成不仅与目标分布匹配,而且与训练数据具有相似分布的样本。
8.1 在 NumPy 中的实现
import numpy as npdef kl_divergence_loss(p, q):return np.sum(p * np.log(p / q))在此实现中,和 是分别表示真实分布和预测分布的 numpy 数组。KL 背离损失使用上述公式计算。pq
请注意,此实现假定并具有相同的形状。如果它们具有不同的形状,则可能需要相应地修改实现。pq
8.2 TensorFlow 中的实现
tf.keras.losses.KLDivergence()是 TensorFlow 中的一个内置函数,用于计算两个概率分布之间的 KL 背离损失。它可以用作各种机器学习任务中的损失函数,例如图像生成、文本生成和强化学习。
下面是一个用法示例:tf.keras.losses.KLDivergence()
import tensorflow as tf# define true distribution and predicted distribution
p = tf.constant([0.2, 0.3, 0.5])
q = tf.constant([0.4, 0.3, 0.3])# compute KL divergence loss
kl_loss = tf.keras.losses.KLDivergence()(p, q)print(kl_loss.numpy()) 在此示例中,和 是 TensorFlow 张量分别表示真实分布和预测分布。该函数用于计算 和 之间的 KL 散度损失。结果是一个表示损失值的标量张量。pqtf.keras.losses.KLDivergence()pq
请注意,通过将 和 具有不同形状的情况广播到通用形状,自动处理这些情况。此外,您还可以通过设置函数的参数来调整 KL 散度损失相对于模型中其他损失的权重,该参数控制损失的聚合方式。tf.keras.losses.KLDivergence()pqreduction
8.3 在 PyTorch 中的实现
在 PyTorch 中,KL 散度损失可以使用模块计算。下面是一个示例实现:torch.nn.KLDivLoss
import torchdef kl_divergence_loss(p, q):criterion = torch.nn.KLDivLoss(reduction='batchmean')loss = criterion(torch.log(p), q)return lossIn this implementation, p and q are PyTorch tensors representing the true distribution and predicted distribution, respectively. The torch.nn.KLDivLoss module is used to compute the KL divergence loss between p and q. The reduction parameter is set to 'batchmean' to compute the mean loss over the batch. 请注意,和 应该是概率,沿最后一个维度的总和为 1。该函数用于在将 的对数传递给模块之前获取对数。这是因为模块期望输入是对数概率。pqtorch.logptorch.nn.KLDivLoss
九、平均绝对误差 (MAE) 损耗 / L1 损耗
L1 损失,也称为平均绝对误差 (MAE) 损失,是深度学习中用于回归任务的常见损失函数。它测量目标变量的预测值和真实值之间的绝对差异。
L1损失的公式为:
L1 LOSS = 1/n * Σ|y_pred — y_true|
其中 n 是样本数,y_pred 是预测值,y_true 是真实值。
简单来说,L1 损失是预测值和真实值之间绝对差值的平均值。它对异常值的敏感度低于均方误差 (MSE) 损失,因此对于可能受异常值影响的模型来说,它是一个不错的选择。
9.1 在 Numpy 中的实现
import numpy as npdef l1_loss(y_pred, y_true):loss = np.mean(np.abs(y_pred - y_true))return lossL1 损失的 NumPy 实现与公式非常相似,其中您从真实值中减去预测值并取绝对值。然后,取所有样本中这些绝对差异的平均值,以获得平均 L1 损失。
9.2 TensorFlow 中的实现
import tensorflow as tfdef l1_loss(y_pred, y_true):loss = tf.reduce_mean(tf.abs(y_pred - y_true))return loss在 TensorFlow 中,您可以使用该函数计算所有样本中预测值和真实值之间的绝对差值的平均值。tf.reduce_mean()
9.3 在 PyTorch 中的实现
import torchdef l1_loss(y_pred, y_true):loss = torch.mean(torch.abs(y_pred - y_true))return loss在 PyTorch 中,您可以使用该函数计算所有样本中预测值和真实值之间的绝对差值的平均值。torch.mean()
十、Huber 胡贝尔损失
Huber 损失是回归任务中使用的损失函数,它对异常值的敏感度低于均方误差 (MSE) 损失。它被定义为MSE损失和平均绝对误差(MAE)损失的组合,其中损失函数是MSE表示小误差,MAE表示较大误差。这使得Huber损失比MSE损失对异常值更稳健。
Huber 损失函数定义如下:
L(y_pred, y_true) = 1/n * sum(0.5 * (y_pred - y_true)^2) if |y_pred - y_true| <= delta1/n * sum(delta * |y_pred - y_true| - 0.5 * delta^2) otherwise 其中 是样本数,是预测值,是真实值,并且是确定在 MSE 和 MAE 损失之间切换的阈值的超参数。ny_predy_truedelta
当 ,损失函数是 MSE 损失。当 时,损失函数是斜率为 的 MAE 损失。|y_pred - y_true| <= delta|y_pred - y_true| > deltadelta
在实践中,通常设置为平衡 MSE 和 MAE 损耗的值,例如 。delta1.0
10.1 在 Numpy 中的实现
import numpy as npdef huber_loss(y_pred, y_true, delta=1.0):error = y_pred - y_trueabs_error = np.abs(error)quadratic = np.minimum(abs_error, delta)linear = (abs_error - quadratic)return np.mean(0.5 * quadratic ** 2 + delta * linear) 此函数将预测值、真值和超参数作为输入,并返回 Huber 损失。y_predy_truedelta
该函数首先计算预测值和真值之间的绝对误差,然后根据超参数将误差拆分为两个分量。二次分量是 时的 MSE 损耗,线性分量是 时的 MAE 损耗。最后,该函数返回所有样本的平均Huber损失。deltaabs_error <= deltaabs_error > delta
您可以在基于 numpy 的回归任务中使用此函数,方法是使用预测值和真实值以及所需值调用它。delta
10.2 TensorFlow 中的实现
import tensorflow as tfdef huber_loss(y_pred, y_true, delta=1.0):error = y_pred - y_trueabs_error = tf.abs(error)quadratic = tf.minimum(abs_error, delta)linear = (abs_error - quadratic)return tf.reduce_mean(0.5 * quadratic ** 2 + delta * linear)此函数将预测值、真值和超参数作为输入,并返回 Huber 损失。y_predy_truedelta
该函数首先使用该函数计算预测值和真值之间的绝对误差,然后使用 and 运算符根据超参数将误差拆分为两个分量。二次分量是 时的 MSE 损耗,线性分量是 时的 MAE 损耗。最后,该函数使用该函数返回所有样本的平均Huber损失。tf.absdeltatf.minimum-abs_error <= deltaabs_error > deltatf.reduce_mean
您可以在基于 TensorFlow 的回归任务中使用此函数,方法是使用预测值和真实值以及所需值调用它。delta
10.3 在 PyTorch 中的实现
import torch.nn.functional as Fdef huber_loss(y_pred, y_true, delta=1.0):error = y_pred - y_trueabs_error = torch.abs(error)quadratic = torch.min(abs_error, delta)linear = (abs_error - quadratic)return 0.5 * quadratic ** 2 + delta * linear 此函数将预测值、真值和超参数作为输入,并返回 Huber 损失。y_predy_truedelta
该函数首先使用该函数计算预测值和真值之间的绝对误差,然后使用 and 运算符根据超参数将误差拆分为两个分量。二次分量是 时的 MSE 损耗,线性分量是 时的 MAE 损耗。最后,该函数使用公式返回 Huber 损失。torch.absdeltatorch.min-abs_error <= deltaabs_error > delta0.5 * quadratic ** 2 + delta * linear
您可以在基于 PyTorch 的回归任务中使用此函数,方法是使用预测值和真实值以及所需值调用它。delta
相关文章:
)
【深度学习所有损失函数】在 NumPy、TensorFlow 和 PyTorch 中实现(2/2)
一、说明 在本文中,讨论了深度学习中使用的所有常见损失函数,并在NumPy,PyTorch和TensorFlow中实现了它们。 (二-五)见 六、稀疏分类交叉熵损失 稀疏分类交叉熵损失类似于分类交叉熵损失,但在真实标签作为整数而不是独热编码提…...

Hazel 引擎学习笔记
目录 Hazel 引擎学习笔记学习方法思考引擎结构创建工程程序入口点日志系统Premake\MD没有 cpp 文件的项目会出错include 到某个库就要包含这个库的路径,注意头文件展开 事件系统 获取和利用派生类信息预编译头文件抽象窗口类和 GLFWgit submodule addpremake 脚本禁…...
Linux系统下Redis3.2集群
本节主要学习reids主从复制的概念,作用,缺点,流程,搭建,验证,reids哨兵模式的概念,作用,缺点,结构,搭建,验证等。 文章目录 一、redis主从复制 …...
Android图形-合成与显示-SurfaceTestDemo
目录 引言: 主程序代码: 结果呈现: 小结: 引言: 通过一个最简单的测试程序直观Android系统的native层Surface的渲染显示过程。 主程序代码: #include <cutils/memory.h> #include <utils/L…...

高压放大器怎么设计(高压放大器设计方案)
高压放大器是一种用于将低电压信号转换成高电压信号的电子设备,广泛应用于通信、雷达、医疗设备等领域。在设计高压放大器时,需要考虑多种因素,如输入输出信号的特性、电路结构的选择、电源和负载匹配等。本文将介绍高压放大器的设计方法和注…...

SpringBoot yml配置注入
yaml语法学习 1、配置文件 SpringBoot使用一个全局的配置文件 , 配置文件名称是固定的 application.properties 语法结构 :keyvalue application.yml 语法结构 :key:空格 value 配置文件的作用:修改SpringBoot自动…...

中科亿海微乘法器(LPMMULT)
引言 FPGA(可编程逻辑门阵列)是一种可在硬件级别上重新配置的集成电路。它具有灵活性和可重构性,使其成为处理各种应用的理想选择,包括数字信号处理、图像处理、通信、嵌入式系统等。在FPGA中,乘法器是一种重要的硬件资…...
Redis_持久化(AOF、RDB)
6. Redis AOF 6.1 简介 目前,redis的持久化主要应用AOF(Append Only File)和RDF两大机制,AOF以日志的形式来记录每个写操作(增量保存),将redis执行过的所有指令全部安全记录下来(读…...
开源数据库Mysql_DBA运维实战 (部署服务篇)
前言❀ 1.数据库能做什么 2.数据库的由来 数据库的系统结构❀ 1.数据库系统DBS 2.SQL语言(结构化查询语言) 3.数据访问技术 部署Mysql❀ 1.通过rpm安装部署Mysql 2.通过源码包安装部署Mysql 前言❀ 1.数据库能做什么 a.不论是淘宝,吃鸡,爱奇艺…...
【Java学习】System.Console使用
背景 在自学《Java核心技术卷1》的过程中看到了对System.Console的介绍,编写下列测试代码, public class ConsoleTest {public static void main(String[] args) {Console cs System.console();String name cs.readLine("AccountInfo: ");…...

从零学算法154
154.已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums [0,1,4,4,5,6,7] 在变化后可能得到: 若旋转 4 次,则可以得到 [4,5,6,7,0,1,4] 若旋转 7 次&#…...

95 | Python 设计模式 —— 策略模式
策略模式(Strategy Pattern) 引言 策略模式是一种行为型设计模式,它定义了一系列的算法,并将每个算法封装在独立的策略类中,使得这些算法可以相互替换,而不影响客户端的使用。策略模式可以让客户端根据不同的需求选择不同的算法,从而使得系统更加灵活和可扩展。 在本…...
)
【BASH】回顾与知识点梳理(十九)
【BASH】回顾与知识点梳理 十九 十九. 循环 (loop)19.1 while do done, until do done (不定循环)19.2 for...do...done (固定循环)19.3 for...do...done 的数值处理(C写法)19.4 搭配随机数与数组的实验19.5 shell script 的追踪与 debug19.6 what_to_eat-2.sh debug结果解析 该…...
Selenium之css怎么实现元素定位?
世界上最远的距离大概就是明明看到一个页面元素站在那里,但是我却定位不到!! Selenium定位元素的方法有很多种,像是通过id、name、class_name、tag_name、link_text等等,但是这些方法局限性太大, 随着自动…...
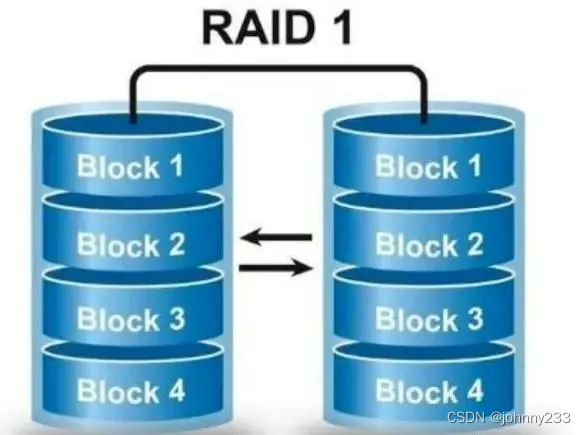
计算机基础之RAID技术
概述 RAID,Redundant Array of Independent Disks,独立磁盘冗余阵列,一种把多块独立的硬盘(物理硬盘)按不同的方式组合起来形成一个硬盘组(逻辑硬盘),从而提供比单个硬盘更高的存储…...

辽宁线上3D三维虚拟工厂生产仿真系统应用场景及优势
工厂虚拟仿真是一种基于计算机技术和虚拟现实技术的数字化解决方案,它可以通过模拟工厂中的设备、流程和操作,来为工程师和操作人员提供了一个沉浸式的虚拟环境,帮助他们更好地了解和优化工厂生产过程。 工厂VR三维可视化技术为工业生产提供了…...
、扩展默认的auth_user表)
csrf跨站请求的相关装饰器、Auth模块(模块的使用、相关方法、退出系统、修改密码功能、注册功能)、扩展默认的auth_user表
一、csrf跨站请求的相关装饰器 django.middleware.csrf.CsrfViewMiddlewareDjango中有一个中间件对csrf跨站做了验证,我只要把csrf的这个中间件打开, 那就意味着所有的方法都要被验证 在所有的视图函数中:只有几个视图函数做验证只有几个函数…...
论文阅读-Detecting Social Media Manipulation in Low-ResourceLanguages)
(WWW2023)论文阅读-Detecting Social Media Manipulation in Low-ResourceLanguages
论文链接:https://arxiv.org/pdf/2011.05367.pdf 摘要 社交媒体被故意用于恶意目的,包括政治操纵和虚假信息。大多数研究都集中在高资源语言上。然而,恶意行为者会跨国家/地区和语言共享内容,包括资源匮乏的语言。 在这里…...

centos-stream-9 centos9 配置国内yum源 阿里云源
源配置 tips: yum配置文件路径 /etc/yum.repos.d/centos.repo 1.备份源配置 [Very Important!]mv /etc/yum.repos.d/centos.repo /etc/yum.repos.d/centos.repo.backup2.Clean Cache: yum clean all3.Backup the Old CentOS-Base.repo If exist this file.cd /etc/yum.repos.…...
查看单元测试用例覆盖率新姿势:IDEA 集成 JaCoCo
1、什么是 IDEA IDEA 全称 IntelliJ IDEA,是 Java 编程语言开发的集成环境。IntelliJ 在业界被公认为最好的 Java 开发工具,尤其在智能代码助手、代码自动提示、重构、JavaEE 支持、各类版本工具(git、SVN 等)、JUnit、CVS 整合、代码分析、 创新的 GUI…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...
