笔记本电脑连上WiFi之后的IP为什么会变?如何让它不变固定住?
笔记本连上WiFi后获取IP地址的过程,通常是通过DHCP (动态主机配置协议) 来完成的。默认情况下,DHCP会根据连接设备和网络状态动态地分配IP地址,因此你会看到IP地址可能经常改变。
如果你希望电脑的IP地址固定,可以尝试设置静态IP地址。以下是设置静态IP的步骤(Windows系统):
打开“控制面板” --> “网络和Internet” --> “网络和共享中心”。
在左侧栏中找到并点击“更改适应器设置”。
右键你所使用的网络适配器(例如:无线网络连接),然后点击“属性”。在弹出的对话框中,找到并双击选择“Internet 协议版本4(TCP/IPv4)”。
选择“使用下面的IP地址”,然后填上你想要设置的固定IP地址,子网掩码和默认网关。
IP地址:这就是你的电脑在网络中的独特地址,通常形如“192.168.1.xxx”。
子网掩码:一般家用路由器的子网掩码是“255.255.255.0”。
默认网关:你的路由器的IP地址即为默认网关,一般形如“192.168.1.1” 或 “192.168.0.1”。
在“使用下面的DNS服务器地址”处填上你想要设置的DNS服务器地址,一般会填写为路由器的IP地址,或者你也可以使用公开的DNS服务器,如Google的公开DNS 8.8.8.8 和 8.8.4.4。
填完后点击“确定”,关闭所有的窗口。
这样就设置好了静态IP地址,之后你的电脑在连接网路时,IP地址就会固定不变。
需要注意的是:静态IP地址设置需要确保不与其他设备的IP地址冲突,否则会导致网络问题。一般可避开DHCP分配的地址范围,或者在路由器设置中为指定MAC地址绑定IP地址。
如果是在公共网络中设置静态IP地址,可能会导致网络无法接入。因此,通常我们在家庭或者公司网络中使用静态IP地址。
相关文章:

笔记本电脑连上WiFi之后的IP为什么会变?如何让它不变固定住?
笔记本连上WiFi后获取IP地址的过程,通常是通过DHCP (动态主机配置协议) 来完成的。默认情况下,DHCP会根据连接设备和网络状态动态地分配IP地址,因此你会看到IP地址可能经常改变。 如果你希望电脑的IP地址固定,可以尝试设置静态IP…...
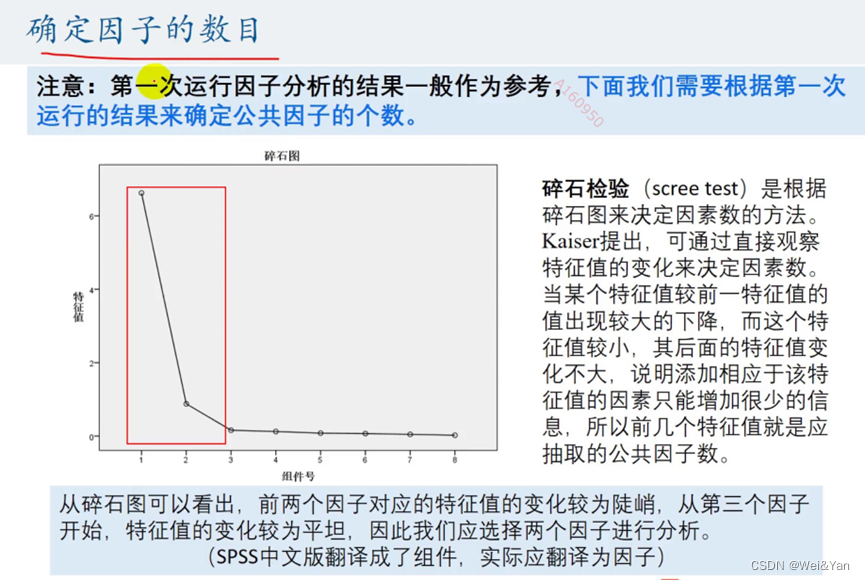
【数学建模】--因子分析模型
因子分析有斯皮尔曼在1904年首次提出,其在某种程度上可以被看成时主成分分析的推广和扩展。 因子分析法通过研究变量间的相关稀疏矩阵,把这些变量间错综复杂的关系归结成少数几个综合因子,由于归结出的因子个数少于原始变量的个数,…...

RAM不够?CUBEIDE使用CCMRAM
RAM不够?使用CCMRAM 文章目录 RAM不够?使用CCMRAM打开连接LD文件:添加代码添加标识宏使用 打开连接LD文件: 添加代码 在SECTIONS段最后加上下面代码: _siccmram LOADADDR(.ccmram); /* CCM-RAM section * * IMPORTAN…...
npm ERR! code ERESOLVEnpm ERR! ERESOLVE unable to resolve dependency tree
拉取项目到本地 执行 npm install 报错 遇到这个问题首先确认的就是版本是不是太高了,降一下版本。或者通过yarn命令替代npm install命令安装,同理,启动也可以采用yarn dev 启动代替npm run dev 下面教大家用一个NVM工具,这个工…...
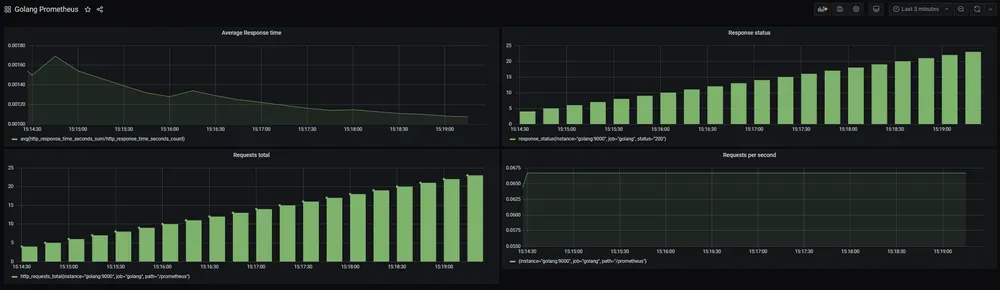
使用 prometheus client SDK 暴露指标
目录 1. 使用 prometheus client SDK 暴露指标1.1. How Go exposition works1.2. Adding your own metrics1.3. Other Go client features 2. Golang Application monitoring using Prometheus2.1. Metrics and Labels2.2. Metrics Types2.2.1. Counters:2.2.2. Gauges:2.2.3. …...

Jmeter之BeanShell取出参数进行四则运算,并判断是否正确
首先调用余额接口,使用正则提取响应中的余额字段,记作变量acctBal1做支付交易再次调用余额接口,使用正则提取响应中的余额字段,记作变量acctBal2最后在结果树中可以看到断言错误的信息,断言正确时没有提示以下是beansh…...
)
PYTHON 斗地主发牌 (简易版)
利用方法: 1. random.randint( ) 随机抽取数字 方法 2.random.sample((抽取范围的参数),(抽取的个数)) 返回的是列表 所以用[0]可以输出里面的元素 import random# 1. 创建牌 # 花色 color ["\u2660", "\u2663", "\u2665", "\…...

CSS文本裁剪
对于单行文本裁剪: span {text-overflow:ellipsis;white-space:nowrap;overflow:hidden;display:block; } 对于多行文本裁剪: 在文本容器上定义 CSS Flexbox 属性 display: -webkit-box; 定义要显示的文本行数 -webkit-line-clamp: 4; 添加 -webkit-…...

ClickHouse常见的引擎和使用
1.日志引擎 日志引擎特点 1.数据存储在磁盘上 2.写入时将数据追加在文件末尾 3.不支持突变操作 4.不支持索引 5.非原子地写入数据 6.引擎不支持 ALTER UPDATE 和 ALTER DELETE 操作 建表语法示例 CREATE TABLE [IF NOT EXISTS] [db.]table_name [ON CLUSTER cluster] ( …...

构建之法 - 软件工程实践教学:一线教师的13问
福州大学单红老师的软工课程总结 2020春,不一样的学期不一样的软工实践 单红⽼师在总结中,提出了13条疑惑,《构建之法》的作者邹欣⽼师就单红⽼师提出的每⼀条疑惑,给出了⾃⼰的思考,与他进⾏探讨交流。欢迎你也来参与…...

联调 matlab 遇到的一些事儿
记录当时遇到的问题,因为平时不写 matlab,所以没有深入的理解。 版本兼容 当时遇到的第一个问题就是不同版本 matlab 带来的兼容性问题。同时开发使用的是 2021a 版本,而调试时使用的是 2022b 版本。在新版本中某些函数已被弃用,…...

时序预测 | Matlab实现基于GRNN广义回归神经网络的电力负荷预测模型
文章目录 效果一览文章概述源码设计参考资料效果一览 文章概述 时序预测 | Matlab实现基于GRNN广义回归神经网络的电力负荷预测模型 1.Matlab实现基于GRNN广义回归神经网络的电力负荷预测模型 2.单变量时间序列预测; 3.多指标评价,评价指标包括:R2、MAE、MBE等,代码质量极高…...
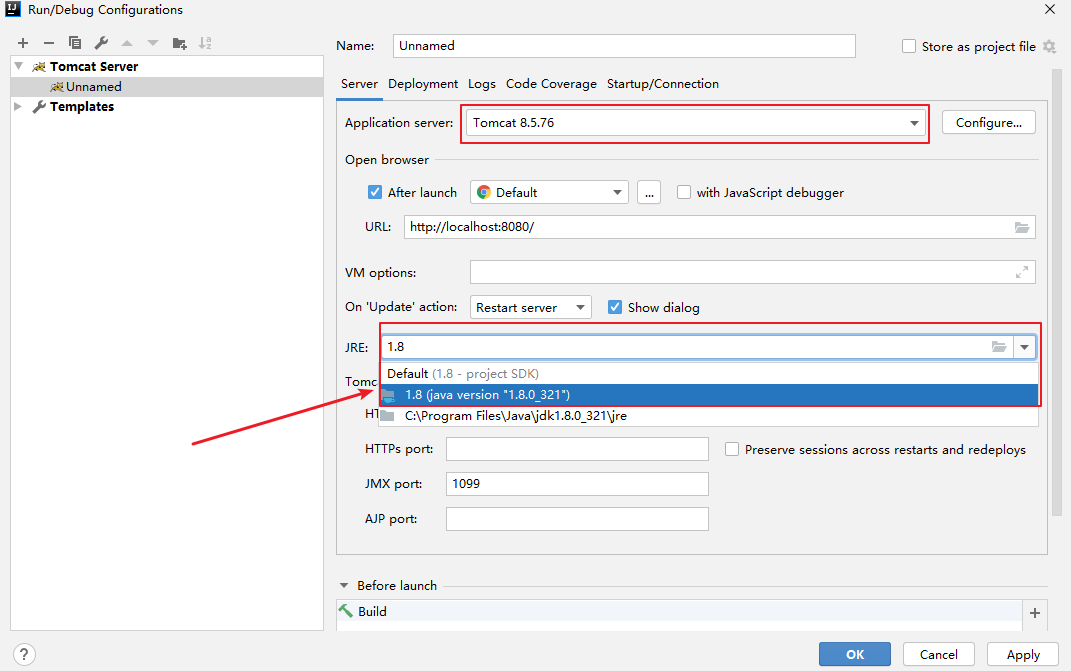
3.2 Tomcat基础
1. Tomcat概述 Tomcat 服务器是一个免费的开放源代码的Web 应用服务器,属于轻量级应用服务器。 Tomcat版本:apache-tomcat-8.5.76。 2.IDEA集成Tomcat 第一步 第二步 第三步 编辑切换为居中 添加图片注释,不超过 140 字࿰…...
认识http的方法、Header、状态码以及简单实现一个http的业务逻辑
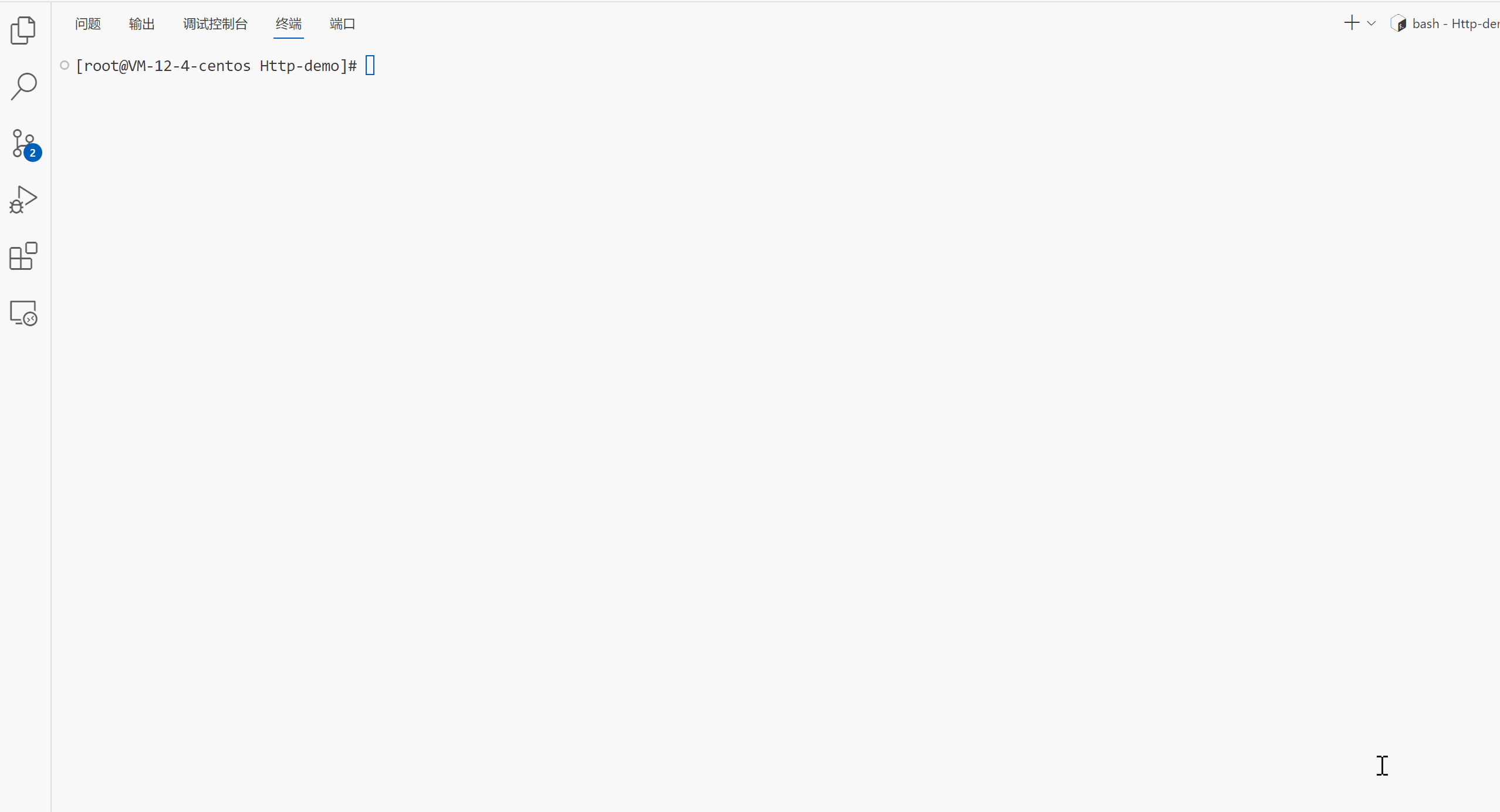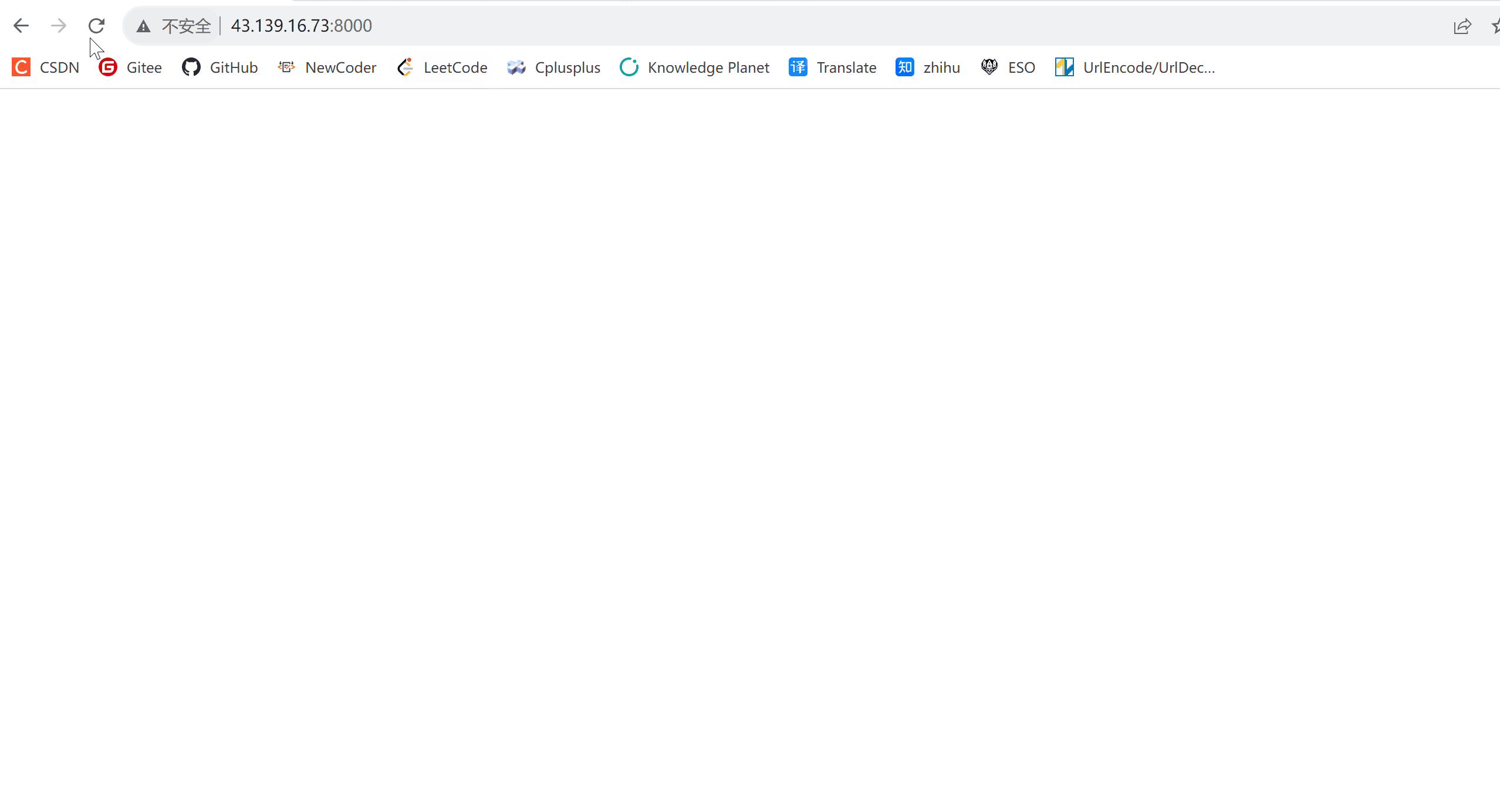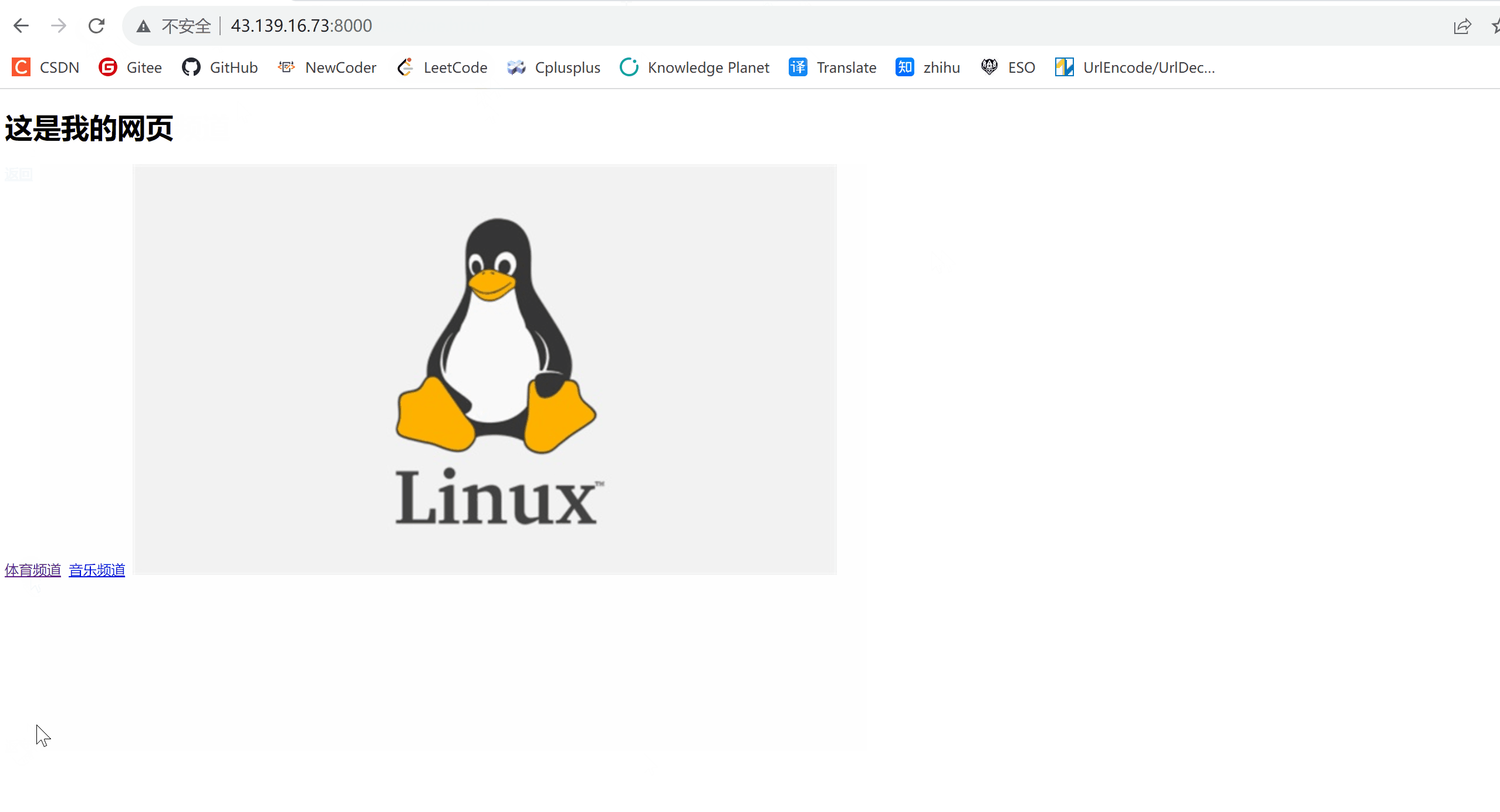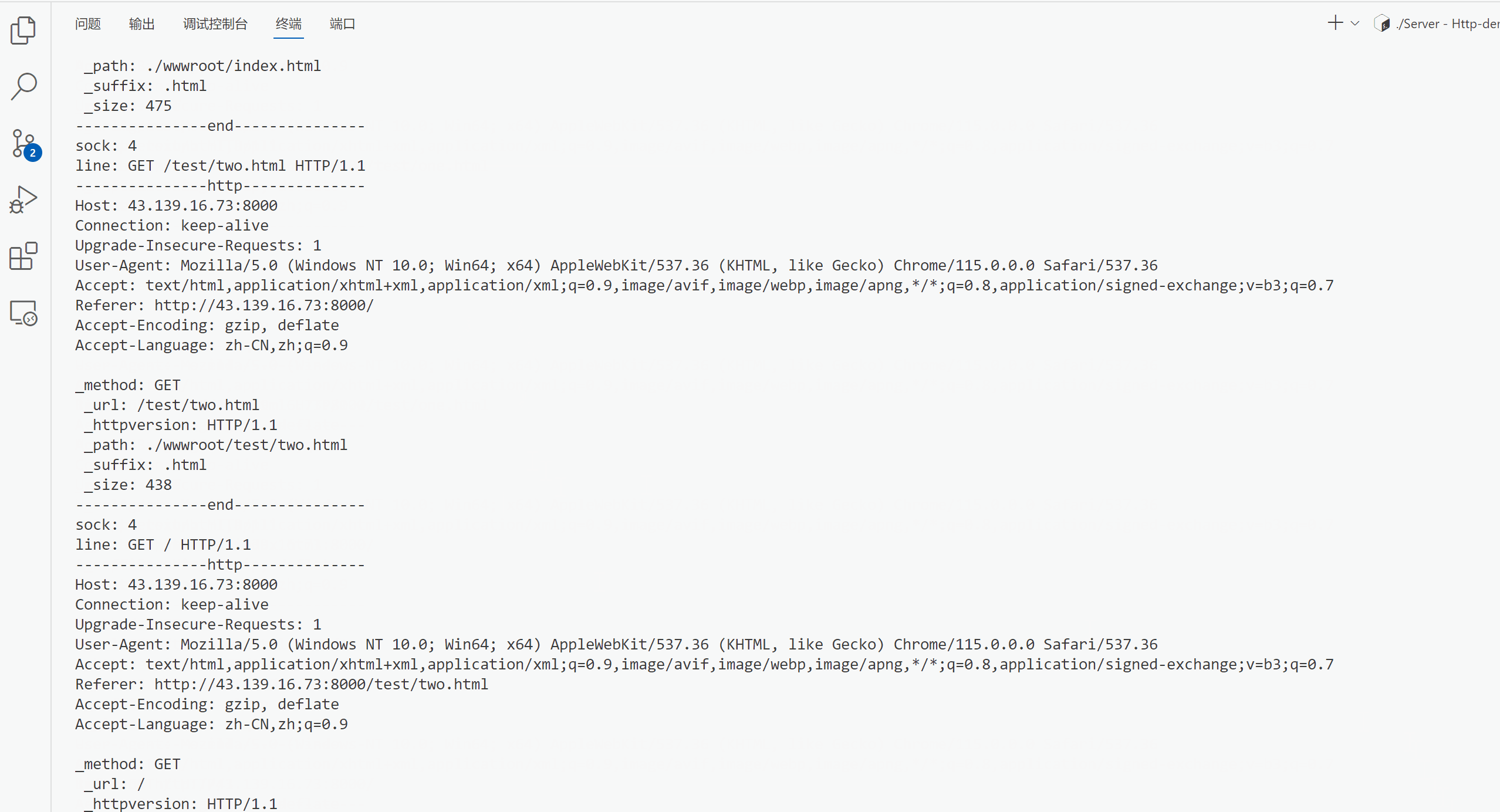
文章目录 http的方法http状态码http重定向http常见Header实现简单业务逻辑Protocol.hppUtil.hppServer.hppServer.cc 效果 http的方法 方法说明支持的HTTP版本GET获取资源1.0/1.1POST传输实体主体1.0/1.1PUT传输文件1.0/1.1HEAD获得报文首部1.0/1.1DELETE删除文件1.0/1.1OPTIO…...

Faiss在windows下安装和使用
pip install faiss-cpu 直接安装可能出现问题: error: command swig.exe failed: No such file or directory 安装swig即可解决,安装方式...
【JavaEE进阶】SpringBoot项目的创建
文章目录 一. SpringBoot简介1. 什么是SpringBoot?2. SpringBoot的优点 二. SpringBoot项目创建1. 使用IDEA创建2. 使用网页创建SpringBoot项目 三. 运行SpringBoot项目 一. SpringBoot简介 1. 什么是SpringBoot? Spring Boot 是一个用于快速构建基于 Spring 框架的应用程序…...
)
c++二进制转化十进制代码(小数)
#include <bits/stdc.h> using namespace std; int mid; double er_shi(string a){int lena;double sum0;int p0;int q-1;int yn1;//判断是否小数 lenaa.length();//字符串长度 for(int i0;i<lena;i){if(a[i].){midi;yn0;break;} }if(yn0){for(int jmid-1;j>0;j--…...

07_ansible, 条件选择、加载客户事件、在roles和includes上面应用’when’语句、条件导入、基于变量选择文件和模版、注册变量
10.条件选择 10.1.When语句 10.2.加载客户事件 10.3.在roles和includes上面应用’when’语句 10.4.条件导入 10.5.基于变量选择文件和模版 10.6.注册变量 10.条件选择 转自:http://www.ansible.com.cn/docs/playbooks_conditionals.html#id3 常常来说,一个play的…...

4个简化IT服务台任务的ChatGPT功能
最近几个月,ChatGPT 风靡全球,这是一个 AI 聊天机器人,使用户能够生成脚本、文章、锻炼图表等。这项技术在各行各业都有无穷无尽的应用,在本文中,我们将研究这种现代技术如何帮助服务台团队增强服务交付和客户体验。 什…...
群晖7.X版安装cpolar内网穿透
群晖7.X版安装cpolar内网穿透套件 文章目录 群晖7.X版安装cpolar内网穿透套件前言1. 下载cpolar的群晖系统套件1.1 在“套件中心” 选择“手动安装”1.2 完成套件安装 2. 进入cpolar软件信息页3. 点击“免费注册”轻松获得cpolar账号 前言 随着群晖系统的更新换代,…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
