当前位置： 首页 > news >正文

【Android】ViewBinding+DataBinding+MVVM新手快速上手

news 2026/2/9 15:01:24

为什么写这篇博客

网上大部分博客，代码量都比较大，把实际的业务都代入进去了

这篇博客的目的，就是为了讲解基本原理和使用思路，然后给出一个最简单的Demo

这里不讲解具体用法，那样篇幅会太长，直接看Demo代码就行

什么是ViewBinding

ViewBinding是一项根据布局文件自动生成所有控件对象的技术，类似于ButterKnife

使用ViewBinding，需要在gradle脚本中开启ViewBinding特性，编译时会自动生成Layout对应的Binding对象

什么是DataBinding

DataBinding是一项将控件内容与对象数值进行绑定的技术

当控件内容发生改变时，对象数值自动改变

当对象数值发生改变时，控件内容也自动改变

android中的DataBinding，主要是通过ViewModel和LiveData这两项技术来实现的

使用ViewBinding，需要在gradle脚本中开启DataBinding特性，这样才能使用ViewModel相关功能

什么是ViewModel和LiveData

ViewModel是一个特殊的数值容器，它可以与布局中的控件进行双向绑定，从而实现数值自动同步

ViewModel的生命周期与Activity或Fragment进行绑定，能够自动销毁

LiveData也是一个特殊的数值容器，它可以对数值变化进行监听，从而实现响应式编程特性

ViewModel和LiveData使用方法

定义ViewModel，其中的数值通过LiveData包装

在xml中，通过layout标签+data标签+变量表达式的方式，来让控件与ViewModel中的值绑定

在Activity中创建ViewModel

在Activity中为ViewModel中的LiveData添加数值监听

在Activity中为ViewModel设置初始值

将ViewModel与Binding绑定

布局内容发生变化时，LiveData会自动更新

手动修改LiveData时，需要通过setValue或postValue来通知订阅者

如何通过ViewModel和LiveData实现MVVM架构

创建ViewModel，将布局文件中需要绑定的属性添加到其中

在ViewModel中创建DataRepository，用于获取和处理数据，这个类就是负责model层工作

在Activity中，通过ViewModel订阅DataRepository处理结果，处理结果可以通过LiveData或RxJava来订阅

源码

ViewBinding+DataBinding+MVVM.zip

相关文章：

【Android】ViewBinding+DataBinding+MVVM新手快速上手

为什么写这篇博客 网上大部分博客，代码量都比较大，把实际的业务都代入进去了 这篇博客的目的，就是为了讲解基本原理和使用思路，然后给出一个最简单的Demo 这里不讲解具体用法，那样篇幅会太长，直接看Demo…...

编程日记 2023/8/13 5:15:55

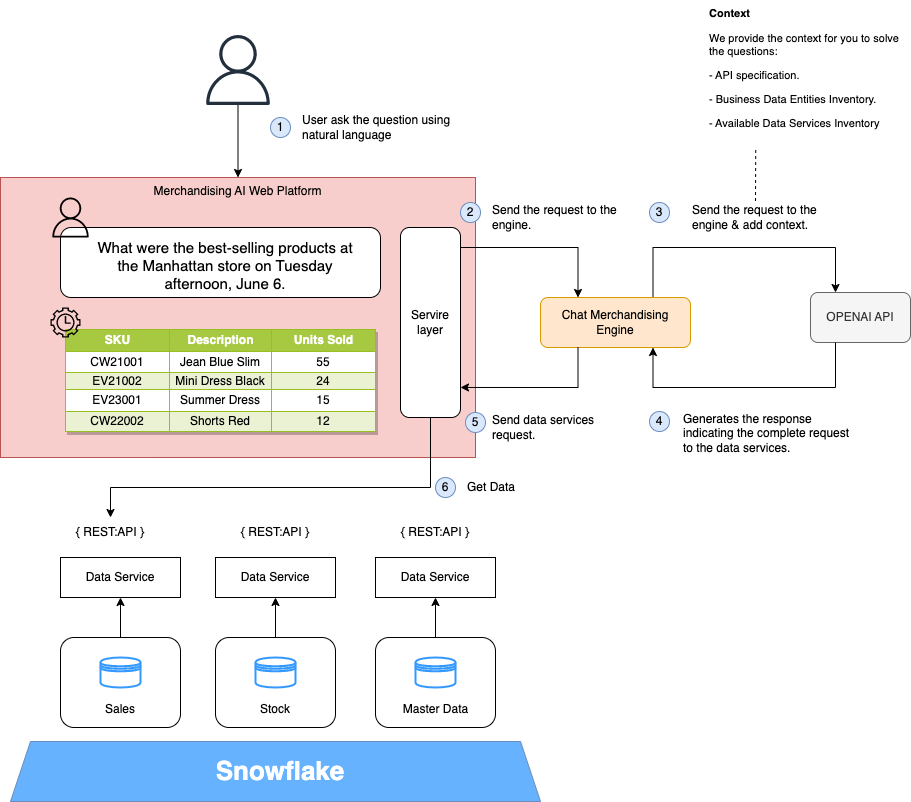
生成式人工智能模型：提升营销分析用户体验

使用生成式人工智能来改善分析体验，使业务用户能够询问有关我们数据平台中可用数据的任何信息。 在本文中，我们将解释如何使用新的生成式人工智能模型 ( LLM ) 来改善业务用户在我们的分析平台上的体验。假设我们为零售销售经理提供 Web 应用程序或移动应…...

编程日记 2023/8/13 5:14:53

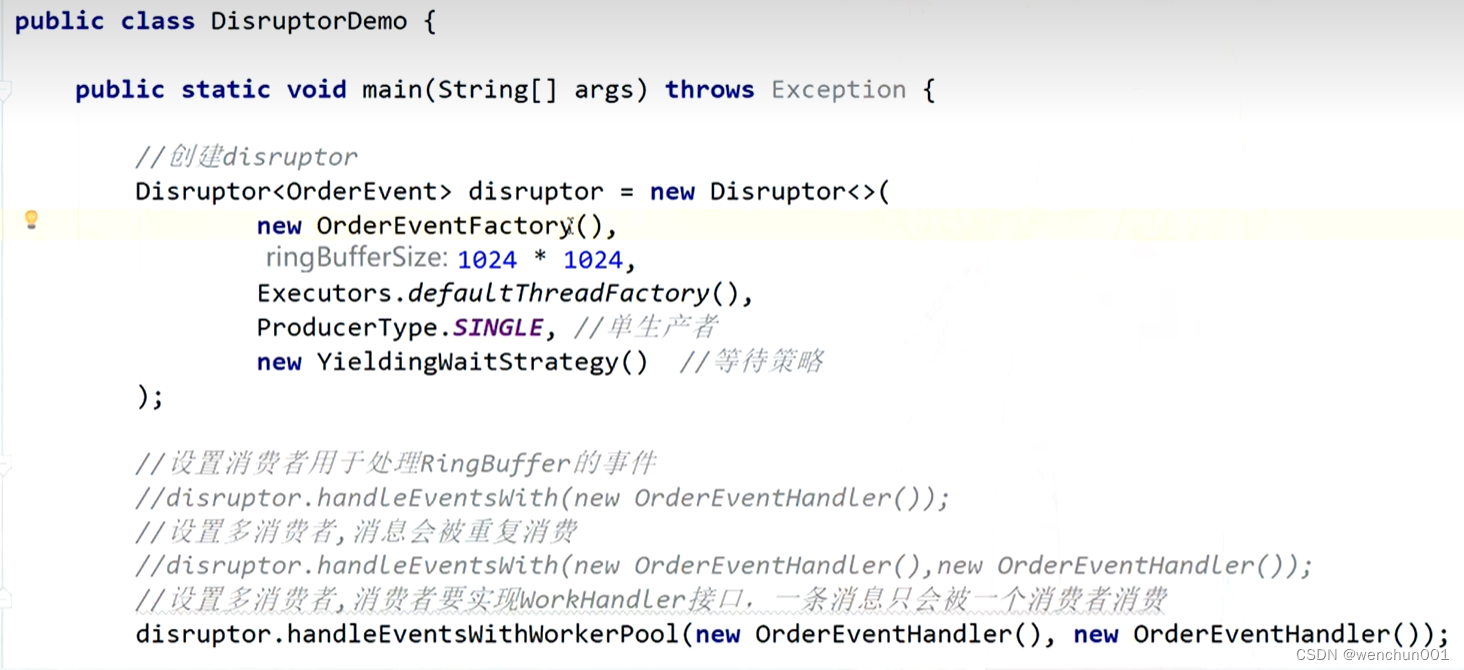
【并发编程】无锁环形队列Disruptor并发框架使用

Disruptor 是苹国外厂本易公司LMAX开发的一个高件能列，研发的初夷是解决内存队列的延识问顾在性能测试中发现竟然与10操作处于同样的数量级)，基于Disruptor开发的系统单线程能支撑每秒600万订单，2010年在QCn演讲后，获得了业界关注…...

编程日记 2023/8/13 5:13:50

【C语言】初阶指针详解

大家好，我是苏貝，本篇博客带大家了解C语言中令人头疼的指针，如果大家觉得我写的不错的话，可以给我一个赞👍吗，感谢❤️ 使用的是VS2019编译器，默认为32位平台 文章目录 ①指针是什么②指针定义与…...

编程日记 2023/8/13 5:12:49

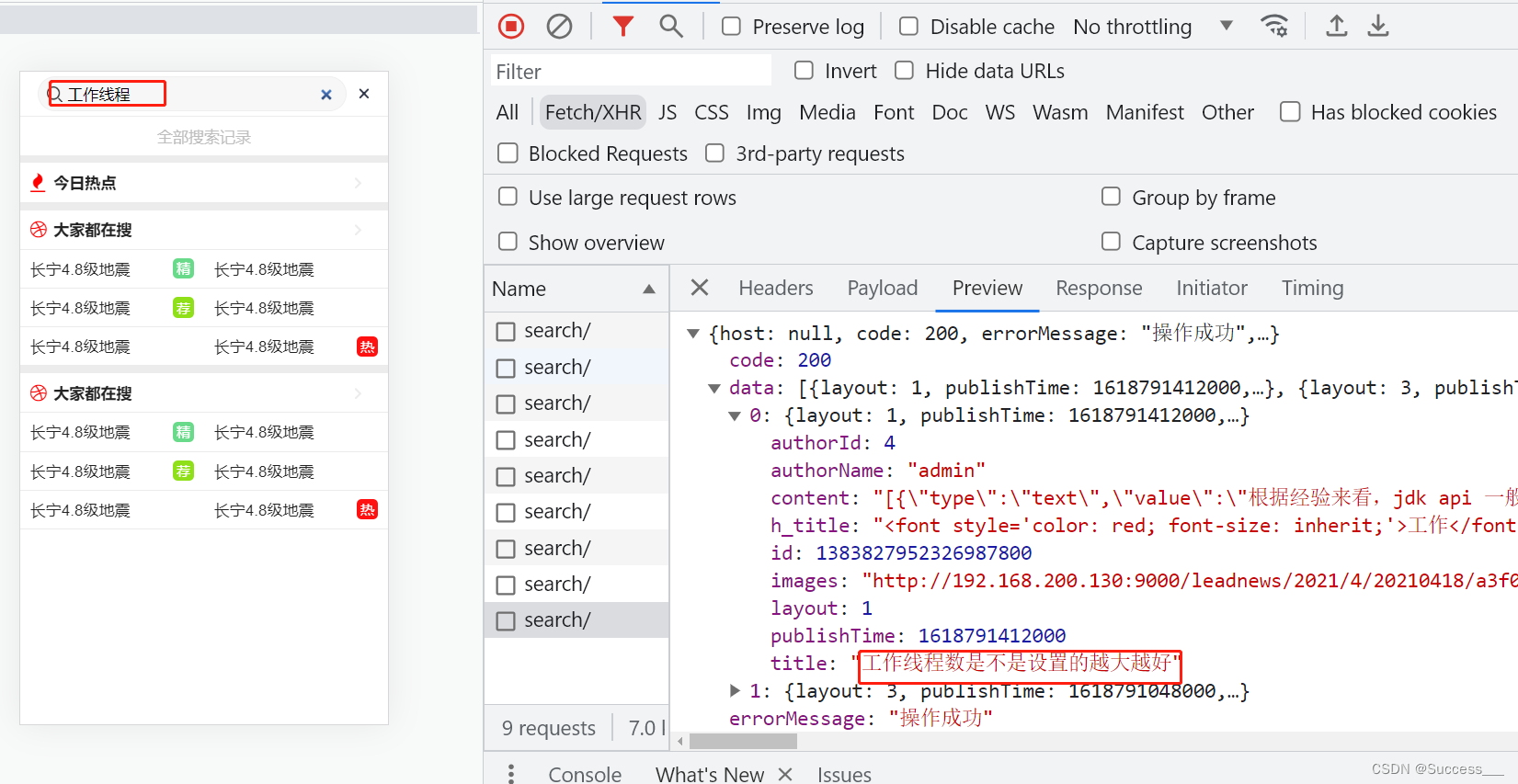
ElasticSearch：项目实战（1）

es环境搭建参考：ElasticSearch：环境搭建步骤_Success___的博客-CSDN博客 需求： 用户输入关键可搜索文章列表 关键词高亮显示 文章列表展示与home展示一样，当用户点击某一篇文章，可查看文章详情 思路： …...

编程日记 2023/8/13 5:11:48

React 实现文件分片上传和下载

React 实现文件分片上传和下载 在开发中，文件的上传和下载是常见的需求。然而，当面对大型文件时，直接的上传和下载方式可能会遇到一些问题，比如网络传输不稳定、文件过大导致传输时间过长等等。为了解决这些问题，我们…...

编程日记 2023/8/13 5:10:47

2023.8.13

atcoder_abc\AtCoder Beginner Contest 310\E_NAND_repeatedly //题意&#xff1a;给定一个n长度的01串&#xff0c;计算f(l,r)(l<r,l在1~n,r在1~n)的和,f的计算(ai,a(i1))运算,有0就为1,11为0 //若f(l,r)1,则f(l,r-1)为0或sr为0,即只取决于上一位的情况和当前位&#xff…...

编程日记 2023/8/13 5:09:45

kvm not all arguments converted during string

kylin virt-manager 远程镜像制作问题记录(not all arguments ) 项目场景&#xff1a; 服务器端安装的OS版本&#xff1a;Kylin-Server-10-SP1-Release-Build20-20210518-arm64-2021-05-18 客户端安装的OS版本&#xff1a;Kylin-Server-10-SP1-Release-Build20-20210518-x86_…...

编程日记 2023/8/13 5:08:44

JVM 基础

巩固基础&#xff0c;砥砺前行 。 只有不断重复&#xff0c;才能做到超越自己。 能坚持把简单的事情做到极致&#xff0c;也是不容易的。 JVM 类加载机制 JVM 类加载机制分为五个部分&#xff1a;加载&#xff0c;验证&#xff0c;准备&#xff0c;解析&#xff0c;初始化&am…...

编程日记 2023/8/13 5:07:40

智谷星图赵俊：让人才和区块链产业“双向奔赴”丨对话MVP

区块链产业需要什么样的人才&#xff1f;赵俊很有发言权。 赵俊是北京智谷星图科技有限公司的技术总监&#xff0c;也是FISCO BCOS官方认证讲师。他2017年接触区块链&#xff0c;随后选择人才培育领域深耕。“为区块链行业引进更多人才这件事很有价值&#xff0c;跟我的职业理…...

编程日记 2023/8/13 5:06:39

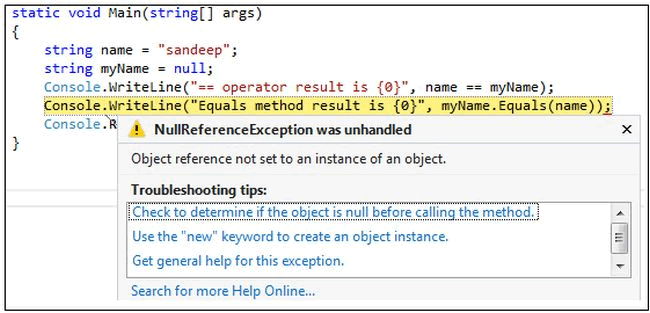
C# Equals()方法报错：NullReferenceException was unhandled

下面是一个C# Equals()方法的例子&#xff0c;执行时报错了 static void Main(string[] args) {string name "sandeep";string myName null;Console.WriteLine(" operator result is {0}", name myName);Console.WriteLine("Equals method result…...

编程日记 2023/8/13 5:05:38

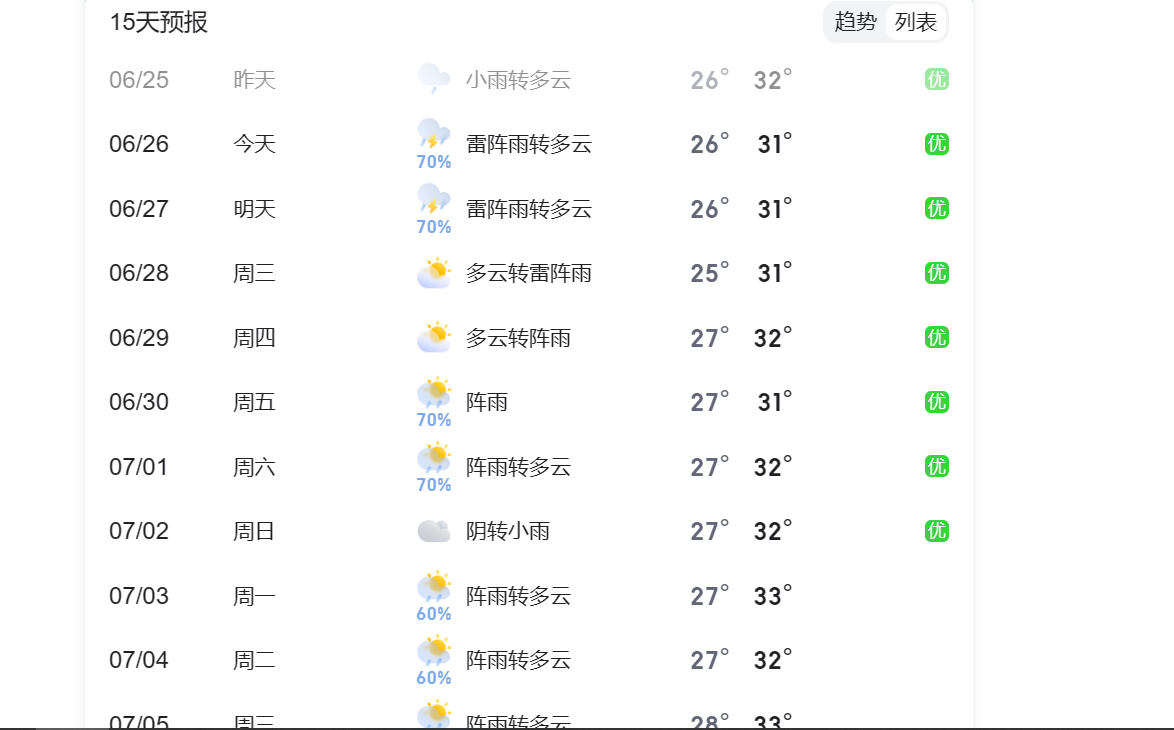
Linux下C语言调用libcurl库获取天气预报信息

一、概述 当前文章介绍如何在Linux&#xff08;Ubuntu&#xff09;下使用C语言调用libcurl库获取天气预报的方法。通过HTTP GET请求访问百度天气API&#xff0c;并解析返回的JSON数据&#xff0c;可以获取指定城市未来7天的天气预报信息。 二、设计思路 【1】使用libcurl库进…...

编程日记 2023/8/13 5:04:36

“深入解析JVM：Java虚拟机原理和内部结构“

标题&#xff1a;深入解析JVM&#xff1a;Java虚拟机原理和内部结构 摘要&#xff1a;本文将深入解析JVM&#xff08;Java虚拟机&#xff09;的原理和内部结构。我们将从JVM的基础概念开始&#xff0c;逐步介绍其组成部分&#xff0c;包括类加载器、运行时数据区、字节码解释器…...

编程日记 2023/8/13 5:03:34

Arrays.asList() 返回的list不能add,remove

一.Arrays.asList() 返回的list不能add,remove Arrays.asList()返回的是List,而且是一个定长的List&#xff0c;所以不能转换为ArrayList&#xff0c;只能转换为AbstractList 原因在于asList()方法返回的是某个数组的列表形式,返回的列表只是数组的另一个视图,而数组本身并没…...

编程日记 2023/8/13 5:02:33

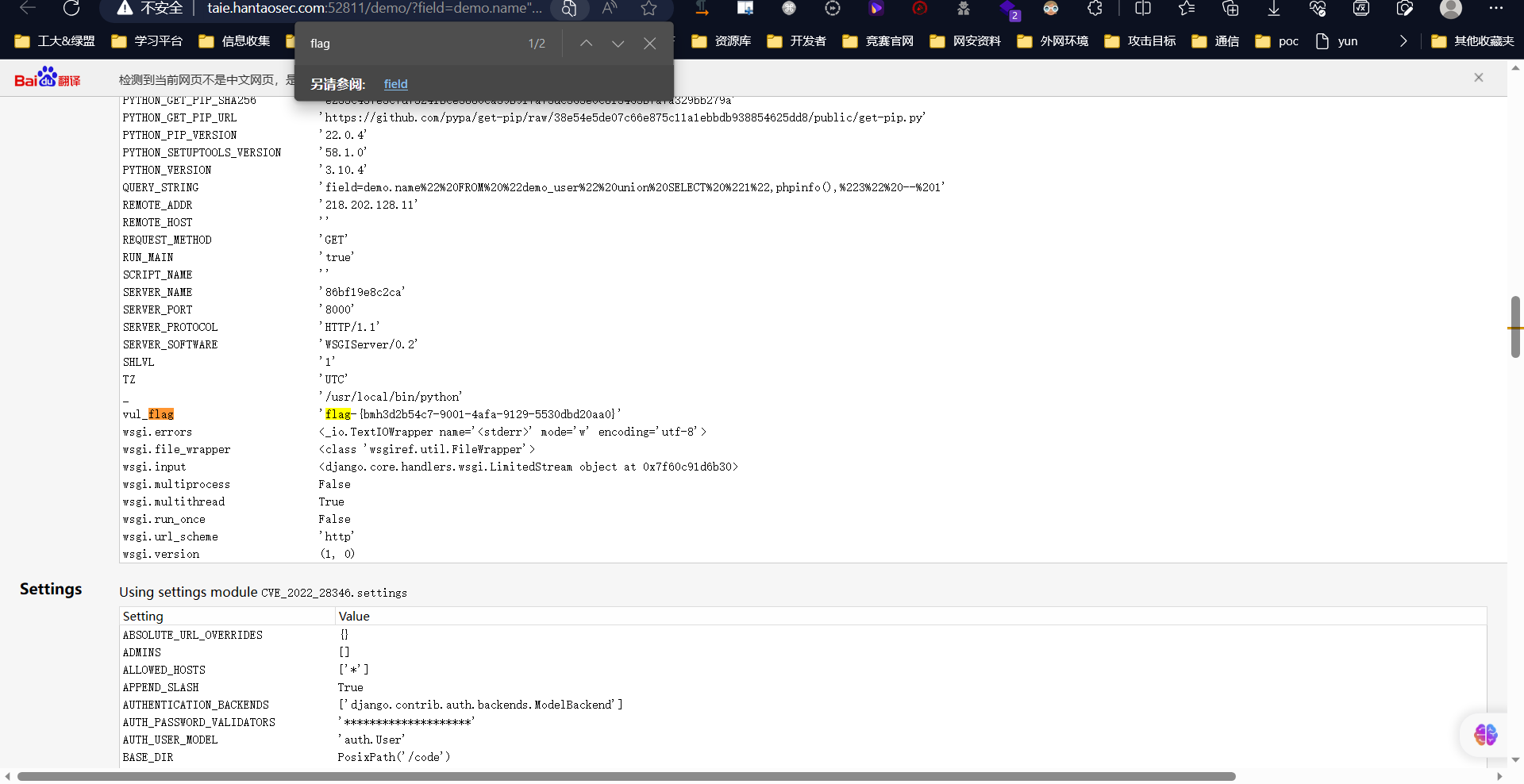
命令执行漏洞

1、命令执行漏洞 1.1、简介 Django是用Python开发的一个免费开源的Web结构&#xff0c;几乎包括了Web使用方方面面&#xff0c;能够用于快速建立高性能、文雅的网站&#xff0c;Diango提供了许多网站后台开发常常用到的模块&#xff0c;使开发者可以专注于业务部分。 1.2、漏…...

编程日记 2023/8/13 5:01:32

Hive 中 sort by 和 order by 的区别

文章目录 数据量大小区别作用范围 在 Hive 中&#xff0c; SORT BY 和 ORDER BY 都用于对查询结果进行排序&#xff0c;但它们在实现方式和适用场景上有一些区别。 数据量大小区别 SORT BY&#xff1a; SORT BY 用于在 Hive 中对查询结果进行排序&#xff0c;它的主要特点是在…...

编程日记 2023/8/13 5:00:31

网络资源利用最大化：爬虫带宽优化解决方案

大家好&#xff0c;作为一名专业的爬虫程序员&#xff0c;我们都知道在爬取大量数据的过程中&#xff0c;网络带宽是一个十分宝贵的资源。如果我们不合理地利用网络带宽&#xff0c;可能会导致爬虫任务的效率低下或者不稳定。今天&#xff0c;我将和大家分享一些优化爬虫带宽利…...

编程日记 2023/8/13 4:59:30

STDF - 基于 Svelte 和 Tailwind CSS 打造的移动 web UI 组件库，Svelte 生态里不可多得的优秀项目

Svelte 是一个新兴的前端框架&#xff0c;组件库不多&#xff0c;今天介绍一款 Svelte 移动端的组件库。 关于 STDF STDF 是一个移动端的 UI 组件库&#xff0c;主要用来开发移动端 web 应用。和我之前介绍的很多 Vue 组件库不一样&#xff0c;STDF 是基于近来新晋 js 框架 S…...

编程日记 2023/8/13 4:58:29

C语言一些有趣的冷门知识

文章目录 概要1.访问数组元素的方法运行结果 2.中括号的特殊用法运行结果 3.大括号的特殊用法运行结果 4.sizeof的用法运行结果 5.渐进运算符运行结果 小结 概要 本文章只是介绍一些有趣的C语言知识&#xff0c;纯属娱乐。这里所有的演示代码我是使用的编译器是Visual Studio …...

编程日记 2023/8/13 4:57:27

Oracle数据库审计

1.什么是审计 审计是用来监控和记录用户的数据库操作的 2.审计级别 语句审计权限审计对象审计 3.查看审计功能是否开启&#xff1a; show parameter audit;相关参数&#xff1a; audit_file_destOS中审计信息存放位置audit_sys_operations默认值为FALSE&#xff0c;即不审…...

编程日记 2023/8/13 4:56:26

Cursor实现用excel数据填充word模版的方法

cursor主页&#xff1a;https://www.cursor.com/ 任务目标&#xff1a;把excel格式的数据里的单元格&#xff0c;按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例&#xff0c;…...

编程新知 2025/8/23 5:46:26

Spark 之 入门讲解详细版（1）

1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室&#xff08;Algorithms, Machines, and People Lab&#xff09;开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目&#xff0c;8个月后成为Apache顶级项目&#xff0c;速度之快足见过人之处&…...

编程新知 2026/2/5 4:17:31

css实现圆环展示百分比，根据值动态展示所占比例

代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

编程新知 2026/2/5 4:28:28

【力扣数据库知识手册笔记】索引

索引 索引的优缺点 优点1. 通过创建唯一性索引&#xff0c;可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度&#xff08;创建索引的主要原因&#xff09;。3. 可以加速表和表之间的连接&#xff0c;实现数据的参考完整性。4. 可以在查询过程中&#xff0c;…...

编程新知 2026/1/25 4:36:37

sqlserver 根据指定字符 解析拼接字符串

DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

编程新知 2025/10/29 4:33:03

LLM基础1_语言模型如何处理文本

基于GitHub项目&#xff1a;https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken&#xff1a;OpenAI开发的专业"分词器" torch&#xff1a;Facebook开发的强力计算引擎&#xff0c;相当于超级计算器 理解词嵌入&#xff1a;给词语画"…...

编程新知 2025/9/25 5:16:24

Ascend NPU上适配Step-Audio模型

1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统&#xff0c;支持多语言对话&#xff08;如 中文&#xff0c;英文&#xff0c;日语&#xff09;&#xff0c;语音情感&#xff08;如 开心&#xff0c;悲伤&#xff09;&#x…...

编程新知 2026/1/31 4:37:39

Web 架构之 CDN 加速原理与落地实践

文章目录 一、思维导图二、正文内容&#xff08;一&#xff09;CDN 基础概念1. 定义2. 组成部分 &#xff08;二&#xff09;CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 &#xff08;三&#xff09;CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 &#xf…...

编程新知 2025/9/13 16:17:01

如何在网页里填写 PDF 表格？

有时候&#xff0c;你可能希望用户能在你的网站上填写 PDF 表单。然而&#xff0c;这件事并不简单&#xff0c;因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件&#xff0c;但原生并不支持编辑或填写它们。更糟的是&#xff0c;如果你想收集表单数据&#xff…...

编程新知 2026/2/6 22:20:51

Java线上CPU飙高问题排查全指南

一、引言 在Java应用的线上运行环境中&#xff0c;CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时&#xff0c;通常会导致应用响应缓慢&#xff0c;甚至服务不可用&#xff0c;严重影响用户体验和业务运行。因此&#xff0c;掌握一套科学有效的CPU飙高问题排查方法&…...

编程新知 2025/11/2 5:30:15