当前位置： 首页 > news >正文

P2P 网络，PING程序。

news 2026/2/11 3:31:28

没有废话，直接上版本号和代码，以及讲解。

crate版本号
libp2p0.52.1
tokio1.30.0

依赖配置：

[dependencies]
tokio = { version="1.30.0", features=["full"] }
libp2p = { version="0.52.1", features=["tokio","dns", "macros", "noise", "ping", "tcp", "websocket", "yamux"] }

P2P

Peer-to-Peer是一种网络技术。一种点对点的通讯技术。没有client-service概念。

节点

在P2P网络中，节点标识被成为PeerId。

代码

use std::error::

相关文章：

P2P 网络，PING程序。

没有废话，直接上版本号和代码，以及讲解。 crate版本号libp2p0.52.1tokio1.30.0依赖配置： [dependencies] tokio = { version="1.30.0", features=["full"] } libp2p = { version="0.52.1", features=["tokio","dns", &q…...

编程日记 2023/8/13 5:39:30

OPENCV C++(十二)模板匹配

正常模板匹配函数 matchTemplate(img, templatee, resultMat, 0);//模板匹配 这里0代表的是方法，一般默认为0就ok img是输入图像 templatee是模板 resultmat是输出 1、cv::TM_SQDIFF：该方法使用平方差进行匹配，因此最佳的匹配结果在结果为…...

编程日记 2023/8/13 5:38:29

【配置环境】Linux下安装MySQL

目录 一，环境 二，安装步骤 1.使用包管理器安装MySQL 2.配置MySQL的安全选项 3.设置root用户使用密码进行身份验证（可选） 三，拓展知识 1.如何修改MySQL的密码策略？ 一，环境 VMware Workst…...

编程日记 2023/8/13 5:37:28

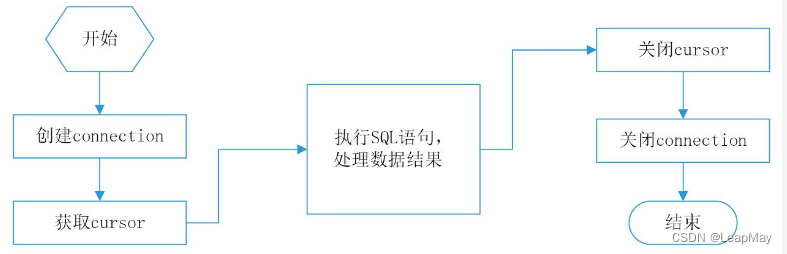
【100天精通python】Day30：使用python操作数据库_数据库基础入门

专栏导读 专栏订阅地址：https://blog.csdn.net/qq_35831906/category_12375510.html 1 数据库基础知识介绍 1.1 什么是数据库？ 数据库是一个结构化存储和组织数据的集合，它可以被有效地访问、管理和更新。数据库的目的是为了提供一种可靠的…...

编程日记 2023/8/13 5:36:27

android 如何分析应用的内存（十八）终章——使用Perfetto查看内存与调用栈之间的泄露

android 如何分析应用的内存（十八） 在前面两篇文章中，先是介绍了如何用AS查看Android的堆内存，然后介绍了使用MAT查看 Android的堆内存。AS能够满足基本的内存分析需求，但是无法进行多个堆的综合比较，因此…...

编程日记 2023/8/13 5:35:25

arcpy实现kml批量转出为shp 包括shp合并

参考文章 arcpy实现 kml批量转出为shp_kml批量合并转shp_A873054267的博客-CSDN博客 参考帮助是arcgis里边自带的KMLToLayer_conversion函数 应用场景： 两步路产生的多个轨迹文件KML，批量转换成arcgis 的gdb数据库 最后合并成一个shp 第一步&#…...

编程日记 2023/8/13 5:34:24

高等数学：泰勒公式

注：第三条 e x e^x ex的展开式，在 1 1 1和 1 2 x 2 \frac{1}{2}x^2 21​x2之间添上一个 x x x。 1 1 − x ∑ n 0 ∞ x n 1 x x 2 x 3 ο ( x 3 ) , x ∈ ( − 1 , 1 ) . \begin{aligned}\frac{1}{1-x}\sum_{n0}^\infty x^n1xx^2x^3\omicron(x^…...

编程日记 2023/8/13 5:33:21

JZ32 从上往下打印二叉树（Java）

题目地址：从上往下打印二叉树_牛客题霸_牛客网 题目回顾： 不分行从上往下打印出二叉树的每个节点，同层节点从左至右打印。例如输入{8,6,10,#,#,2,1}，如以下图中的示例二叉树，则依次打印8,6,10,2,1(空节点不打印&…...

编程日记 2023/8/13 5:32:20

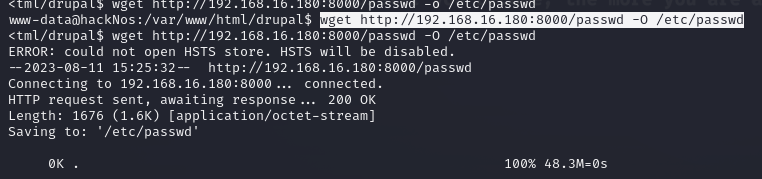
hackNos靶机

靶机训练1 - hackNos: Os-hackNos 靶机平台 Vulnhub 是一个提供各种漏洞环境的靶场平台，供安全爱好者学习使用，大部分环境是做好的虚拟机镜像文件，镜像预先设计了多种漏洞，需要使用VMware或者VirtualBox运行。每个镜像会有破解的目…...

编程日记 2023/8/13 5:31:19

取地址及 const取地址操作符重载

取地址及 const取地址操作符重载 #include <iostream> using namespace std;class A { public:A(int year, int month, int day){_year year;_month month;_day day;}//它们是默认成员函数&#xff0c;我们不写编译器会自动生成&#xff0c;自动生成就够用了&#xff…...

编程日记 2023/8/13 5:30:18

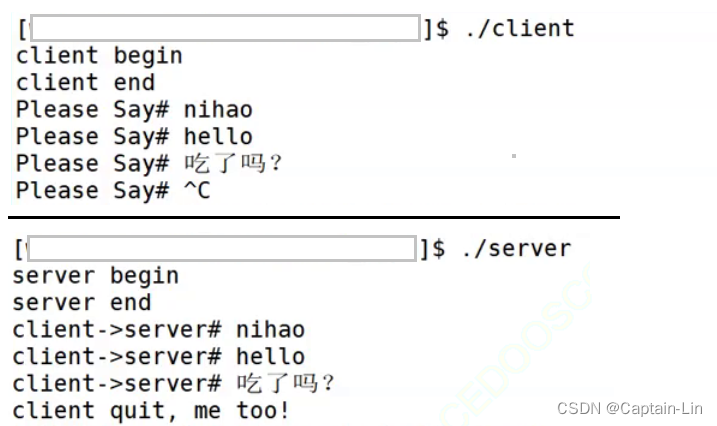
【Linux初阶】进程间通信介绍 管道

&#x1f31f;hello&#xff0c;各位读者大大们你们好呀&#x1f31f; &#x1f36d;&#x1f36d;系列专栏&#xff1a;【Linux初阶】 ✒️✒️本篇内容&#xff1a;进程间通信介绍&#xff0c;管道概述&#xff0c;匿名管道应用&#xff0c;命名管道应用 &#x1f6a2;&#…...

编程日记 2023/8/13 5:29:14

App 在macOS Catalina下提示已损坏无法打开解决办法：

App 在macOS Catalina下提示已损坏无法打开解决办法&#xff1a; 打开终端&#xff1b; 输入以下命令&#xff0c;回车&#xff1b; sudo xattr -d com.apple.quarantine /Applications/xxxx.app注意&#xff1a;/Applications/xxxx.app 换成你的App路径&#xff08;推荐直接…...

编程日记 2023/8/13 5:28:13

ad+硬件每日学习十个知识点（26）23.8.6 （DCDC的降压电路、升压电路、降压-升压电路，同步整流，选型考虑同步、隔离）

文章目录 1.DCDC的降压原理2.DCDC的升压原理3.DCDC的升压和降压原理4.什么是肖特基二极管造成的死区电压&#xff1f;5.MOS管有死区电压么&#xff1f;6.DCDC的同步整流&#xff08;用MOS管取代整流二极管&#xff0c;避免死区电压的影响&#xff09;7.DCDC选型——同步与非同步…...

编程日记 2023/8/13 5:27:12

Elasticsearch3节点集群配置账号密码安全验证

Elasticsearch3节点集群配置账号密码安全验证 ES配置文件 rootnode1:~# grep -Ev "^#|^$" /etc/elasticsearch/elasticsearch.yml cluster.name: es-pre node.name: node1 node.master: true node.data: true path.data: /data/elk/es/data path.logs: /data/elk/…...

编程日记 2023/8/13 5:26:11

ffmepg滤镜

视频按顺时针方向旋转90度 ffplay -vf transpose1 -i juren-30s.mp4 ffplay -f lavfi -i testsrc -vf transpose1 -f lavfi -i testsrc这个滤镜是ffmpeg给用户的一个测试使用的视频 视频水平翻转(左右翻转) -vf hflip 实现慢速播放&#xff0c;声音速度是原始速度的50% ffpla…...

编程日记 2023/8/13 5:25:10

Linux 基础（六）常用命令 - find locate which whereis gzip gunzip tar

find & locate & which & whereis & gzip & gunzip & tar findlocatewhichwhereisgzipgunzipzip/unziptar find 在指定目录下查找文件或目录 find --help Usage: find [-H] [-L] [-P] [-Olevel] [-D help|tree|search|stat|rates|opt|exec] [path...…...

编程日记 2023/8/13 5:24:07

【Ajax】回调地狱解决方法

回调地狱&#xff08;Callback Hell&#xff09;是指在异步编程中&#xff0c;特别是在嵌套的回调函数中&#xff0c;代码变得深度嵌套、难以阅读和维护的现象。这通常发生在处理多个异步操作时&#xff0c;每个操作都依赖于前一个操作的结果。回调地狱使代码变得难以理解、扩展…...

编程日记 2023/8/13 5:23:06

解决Vue根组件设置transition失效的问题

解决Vue根组件设置transition失效的问题 1.代码 <div id"app"><!-- :name"$route.meta.transitionName" --><transition :name"animation" mode"out-in"><router-view /></transition></div>&…...

编程日记 2023/8/13 5:22:05

【剑指 Offer 40】最小的k个数

题目&#xff1a; 输入整数数组 arr &#xff0c;找出其中最小的 k 个数。例如&#xff0c;输入 4、5、1、6、2、7、3、8 这 8 个数字&#xff0c;则最小的 4 个数字是 1、2、3、4。 示例&#xff1a; 输入&#xff1a;arr [3,2,1], k 2 输出&#xff1a;[1,2] 或者 [2,1] …...

编程日记 2023/8/13 5:21:04

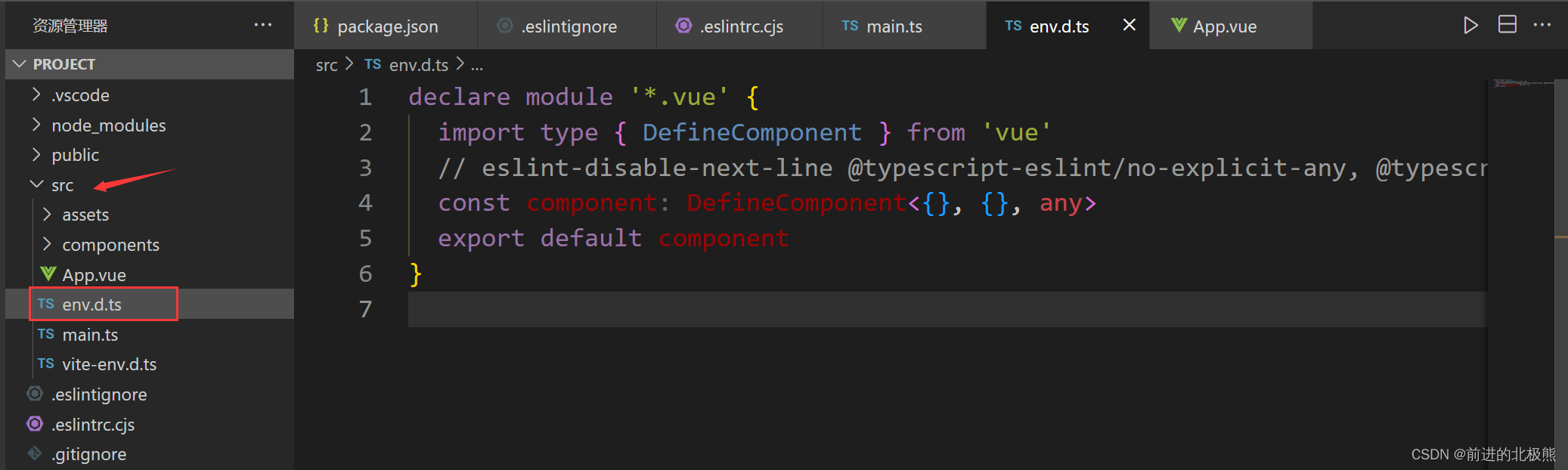
vue3+vite在main.ts文件中引入./App.vue报错（./App.vue不是模块）

问题 如下图&#xff1a; 方法一 下载TypeScript Vue Plugin (Volar)插件就不报红了&#xff0c;看它的描述应该就是ts文件可以识别vue文件。 方法二 在src文件夹下添加env.d.ts文件&#xff0c;添加以下代码&#xff1a; declare module *.vue {import type { DefineC…...

编程日记 2023/8/13 5:20:00

HTML 语义化

目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案&#xff1a; 语义化标签&#xff1a; <header>&#xff1a;页头<nav>&#xff1a;导航<main>&#xff1a;主要内容<article>&#x…...

编程新知 2026/1/15 21:24:41

三维GIS开发cesium智慧地铁教程（5）Cesium相机控制

一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点&#xff1a; 路径验证&#xff1a;确保相对路径.…...

编程新知 2025/12/1 19:23:04

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现，论文初版实现

摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序&#xff0c;以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务&#xff0c;提供稳定高效的数据处理与业务逻辑支持&#xff1b;利用 uniapp 实现跨平台前…...

编程新知 2026/1/31 10:55:22

【RockeMQ】第2节｜RocketMQ快速实战以及核⼼概念详解（二）

升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点&#xff0c;但无自动故障转移能力&#xff0c;Master宕机后需人工切换&#xff0c;期间消息可能无法读取。Slave仅存储数据&#xff0c;无法主动升级为Master响应请求&#xff…...

编程新知 2025/9/2 3:37:40

汇编常见指令

汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX&#xff08;不访问内存&#xff09;XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

编程新知 2026/1/23 2:04:44

精益数据分析（97/126）：邮件营销与用户参与度的关键指标优化指南

精益数据分析&#xff08;97/126&#xff09;&#xff1a;邮件营销与用户参与度的关键指标优化指南 在数字化营销时代&#xff0c;邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天&#xff0c;我们将深入解析邮件打开率、网站可用性、页面参与时…...

编程新知 2025/12/13 4:04:33

Java多线程实现之Thread类深度解析

Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

编程新知 2025/8/28 21:52:02

高考志愿填报管理系统---开发介绍

高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发&#xff0c;采用现代化的Web技术&#xff0c;为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## &#x1f4cb; 系统概述 ### &#x1f3af; 系统定…...

编程新知 2026/1/23 4:26:12

DAY 26 函数专题1

函数定义与参数知识点回顾&#xff1a;1. 函数的定义2. 变量作用域&#xff1a;局部变量和全局变量3. 函数的参数类型&#xff1a;位置参数、默认参数、不定参数4. 传递参数的手段&#xff1a;关键词参数5 题目1&#xff1a;计算圆的面积 任务&#xff1a; 编写一…...

编程新知 2025/11/28 7:53:17

rm视觉学习1-自瞄部分

首先先感谢中南大学的开源&#xff0c;提供了很全面的思路&#xff0c;减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接&#xff1a;https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架&#xff1a; 代码框架结构&#xff1a;readme有…...

编程新知 2026/2/7 21:45:37