高等数学:泰勒公式
注:第三条 e x e^x ex的展开式,在 1 1 1和 + 1 2 x 2 +\frac{1}{2}x^2 +21x2之间添上一个 + x +x +x。
-
1 1 − x = ∑ n = 0 ∞ x n = 1 + x + x 2 + x 3 + ο ( x 3 ) , x ∈ ( − 1 , 1 ) . \begin{aligned}\frac{1}{1-x}=\sum_{n=0}^\infty x^n=1+x+x^2+x^3+\omicron(x^3),x\in(-1,1).\end{aligned} 1−x1=n=0∑∞xn=1+x+x2+x3+ο(x3),x∈(−1,1).
-
1 1 + x = ∑ n = 0 ∞ ( − 1 ) n x n = 1 − x + x 2 − x 3 + ο ( x 3 ) , x ∈ ( − 1 , 1 ) . \begin{aligned}\frac{1}{1+x}=\sum_{n=0}^\infty (-1)^nx^n=1-x+x^2-x^3+\omicron(x^3),x\in(-1,1).\end{aligned} 1+x1=n=0∑∞(−1)nxn=1−x+x2−x3+ο(x3),x∈(−1,1).
-
e x = ∑ n = 0 ∞ x n n ! = 1 + 1 2 x 2 + 1 6 x 3 + ο ( x 3 ) , x ∈ ( − ∞ , + ∞ ) . \begin{aligned}e^x=\sum_{n=0}^\infty \frac{x^n}{n!}=1+\frac{1}{2}x^2+\frac{1}{6}x^3+\omicron(x^3),x\in(-\infty,+\infty).\end{aligned} ex=n=0∑∞n!xn=1+21x2+61x3+ο(x3),x∈(−∞,+∞).
-
sin x = ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! = x − x 3 6 + ο ( x 3 ) , x ∈ ( − ∞ , + ∞ ) . \begin{aligned}\sin x=\sum_{n=0}^\infty(-1)^n\frac{x^{2n+1}}{(2n+1)!}=x-\frac{x^3}{6}+\omicron(x^3),x\in(-\infty,+\infty).\end{aligned} sinx=n=0∑∞(−1)n(2n+1)!x2n+1=x−6x3+ο(x3),x∈(−∞,+∞).
-
cos x = ∑ n = 0 ∞ ( − 1 ) n x 2 n ( 2 n ) ! = 1 − x 2 2 + x 4 24 + ο ( x 4 ) , x ∈ ( − ∞ , + ∞ ) . \begin{aligned}\cos x=\sum_{n=0}^\infty(-1)^n\frac{x^{2n}}{(2n)!}=1-\frac{x^2}{2}+\frac{x^4}{24}+\omicron(x^4),x\in(-\infty,+\infty).\end{aligned} cosx=n=0∑∞(−1)n(2n)!x2n=1−2x2+24x4+ο(x4),x∈(−∞,+∞).
-
tan x = ∑ n = 0 ∞ B 2 n ( − 4 ) n ( 1 − 4 n ) ( 2 n ) ! x 2 n − 1 = x + x 3 3 + ο ( x 3 ) , x ∈ ( − π 2 , π 2 ) . \begin{aligned}\tan x=\sum_{n=0}^\infty\frac{B_{2n}(-4)^n(1-4^n)}{(2n)!}x^{2n-1}=x+\frac{x^3}{3}+\omicron(x^3),x\in(-\frac{\pi}{2},\frac{\pi}{2}).\end{aligned} tanx=n=0∑∞(2n)!B2n(−4)n(1−4n)x2n−1=x+3x3+ο(x3),x∈(−2π,2π).
其中 B 2 n B_{2n} B2n 是 B e r n o u l l i \mathrm{Bernoulli} Bernoulli数,定义为 B n = lim x → 0 d n d x n [ x e x − 1 ] . \begin{aligned}B_n=\lim_{x\rightarrow0}\frac{d^n}{dx^n}[\frac{x}{e^x-1}].\end{aligned} Bn=x→0limdxndn[ex−1x].
-
arcsin x = ∑ n = 0 ∞ ( 2 n ) ! 4 n ( n ! ) 2 × x 2 n + 1 2 n + 1 = x + x 3 6 + ο ( x 3 ) , x ∈ [ − 1 , 1 ] \begin{aligned}\arcsin x=\sum_{n=0}^\infty \frac{(2n)!}{4^n(n!)^2}\times\frac{x^{2n+1}}{2n+1}=x+\frac{x^3}{6}+\omicron(x^3),x\in[-1,1]\end{aligned} arcsinx=n=0∑∞4n(n!)2(2n)!×2n+1x2n+1=x+6x3+ο(x3),x∈[−1,1]
-
arccos x = π 2 − arcsin x = π 2 − ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 2 n + 1 = π 2 − x − x 3 6 + ο ( x 3 ) , x ∈ [ − 1 , 1 ] . \begin{aligned}\arccos x=\frac{\pi}{2}-\arcsin x=\frac{\pi}{2}-\sum_{n=0}^\infty\frac{(-1)^nx^{2n+1}}{2n+1}=\frac{\pi}{2}-x-\frac{x^3}{6}+\omicron(x^3),x\in[-1,1].\end{aligned} arccosx=2π−arcsinx=2π−n=0∑∞2n+1(−1)nx2n+1=2π−x−6x3+ο(x3),x∈[−1,1].
注:一般的 T a y l o r Taylor Taylor公式表里面没有标注 arccos x \arccos x arccosx的原因是, arccos x + arcsin x = π 2 \arccos x+\arcsin x=\frac{\pi}{2} arccosx+arcsinx=2π,也就是说,根据 arcsin x \arcsin x arcsinx的 T a y l o r Taylor Taylor公式,就可以直接推出 $\arccos x 的 的 的Taylor$了。
-
arctan x = ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 2 n + 1 = x − x 3 3 + ο ( x 3 ) , x ∈ [ − 1 , 1 ] . \begin{aligned}\arctan x=\sum_{n=0}^\infty\frac{(-1)^nx^{2n+1}}{2n+1}=x-\frac{x^3}{3}+\omicron(x^3),x\in[-1,1].\end{aligned} arctanx=n=0∑∞2n+1(−1)nx2n+1=x−3x3+ο(x3),x∈[−1,1].
-
a r c c o t x = π 2 − arctan x = π 2 − ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 2 n + 1 = π 2 − x + x 3 3 + ο ( x 3 ) , x ∈ [ − 1 , 1 ] . \begin{aligned}\mathrm{arccot} \,x=\frac{\pi}{2}-\arctan x=\frac{\pi}{2}-\sum_{n=0}^\infty\frac{(-1)^nx^{2n+1}}{2n+1}=\frac{\pi}{2}-x+\frac{x^3}{3}+\omicron(x^3),x\in[-1,1].\end{aligned} arccotx=2π−arctanx=2π−n=0∑∞2n+1(−1)nx2n+1=2π−x+3x3+ο(x3),x∈[−1,1].
这里也是一样,可以直接用 arctan x \arctan x arctanx 的 T a y l o r Taylor Taylor公式推出来,就不作过多解释了。
- a r c s e c x = arccos ( 1 x ) = π 2 − arcsin ( 1 x ) = π 2 − ∑ n = 0 ∞ ( 2 n ) ! 4 n ( n ! ) 2 × ( 1 x ) 2 n + 1 2 n + 1 = π 2 − 1 x − 1 6 x 3 + ο ( x 3 ) , { x ∈ R ∣ x ∉ ( − 1 , 1 ) } . \begin{aligned}\mathrm{arcsec}\,x=\arccos(\frac{1}{x})=\frac{\pi}{2}-\arcsin(\frac{1}{x})\end{aligned} \begin{aligned}=\frac{\pi}{2}-\sum_{n=0}^\infty\frac{(2n)!}{4^n(n!)^2}\times\frac{(\frac{1}{x})^{2n+1}}{2n+1}=\frac{\pi}{2}-\frac{1}{x}-\frac{1}{6x^3}+\omicron(x^3),\{x\in\mathbb{R}|x\notin(-1,1)\}.\end{aligned} arcsecx=arccos(x1)=2π−arcsin(x1)=2π−n=0∑∞4n(n!)2(2n)!×2n+1(x1)2n+1=2π−x1−6x31+ο(x3),{x∈R∣x∈/(−1,1)}.
至于怎么推导出来的,问就是desmos里图像完全一样。
-
a r c c s c x = π 2 − a r c s e c x = π 2 − ( π 2 − arcsin ( 1 x ) ) = arcsin ( 1 x ) = ∑ n = 0 ∞ ( 2 n ) ! 4 n ( n ! ) 2 × ( 1 x ) 2 n + 1 2 n + 1 = 1 x + 1 6 x 3 + ο ( 1 x 3 ) , { x ∈ R ∣ x ∉ ( − 1 , 1 ) } . \begin{aligned}\mathbb{arccsc}\,x=\frac{\pi}{2}-\mathbb{arcsec}\,x=\frac{\pi}{2}-(\frac{\pi}{2}-\arcsin(\frac{1}{x}))=\arcsin(\frac{1}{x})\end{aligned}\begin{aligned}=\sum_{n=0}^\infty \frac{(2n)!}{4^n(n!)^2}\times\frac{(\frac{1}{x})^{2n+1}}{2n+1}=\frac{1}{x}+\frac{1}{6x^3}+\omicron(\frac{1}{x^3}),\{x\in\mathbb R|x\notin(-1,1)\}.\end{aligned} arccscx=2π−arcsecx=2π−(2π−arcsin(x1))=arcsin(x1)=n=0∑∞4n(n!)2(2n)!×2n+1(x1)2n+1=x1+6x31+ο(x31),{x∈R∣x∈/(−1,1)}.
-
ln ( 1 + x ) = ∑ n = 0 ∞ ( − 1 ) n x n + 1 n + 1 = x − 1 2 x 2 + 1 3 x 3 + ο ( x 3 ) , x ∈ ( − 1 , 1 ] . \begin{aligned}\ln(1+x)=\sum_{n=0}^\infty(-1)^n\frac{x^{n+1}}{n+1}=x-\frac{1}{2}x^2+\frac{1}{3}x^3+\omicron(x^3),x\in(-1,1].\end{aligned} ln(1+x)=n=0∑∞(−1)nn+1xn+1=x−21x2+31x3+ο(x3),x∈(−1,1].
-
( 1 + x ) m = 1 + ∑ n = 1 ∞ m ( m − 1 ) ⋯ ( m − n + 1 ) n ! x n , x ∈ ( − 1 , 1 ) . \begin{aligned}(1+x)^m=1+\sum_{n=1}^\infty\frac{m(m-1)\cdots(m-n+1)}{n!}x^n,x\in(-1,1).\end{aligned} (1+x)m=1+n=1∑∞n!m(m−1)⋯(m−n+1)xn,x∈(−1,1).
-
cot x = ∑ n = 0 ∞ ( − 1 ) n 2 2 n B 2 n ( 2 n ) ! x 2 n − 1 = 1 x − 1 3 x − 1 45 x 3 + ο ( x 3 ) , x ∈ ( 0 , π ) . \begin{aligned}\cot x=\sum_{n=0}^\infty\frac{(-1)^n2^{2n}B_{2n}}{(2n)!}x^{2n-1}=\frac{1}{x}-\frac{1}{3}x-\frac{1}{45}x^3+\omicron(x^3),x\in(0,\pi).\end{aligned} cotx=n=0∑∞(2n)!(−1)n22nB2nx2n−1=x1−31x−451x3+ο(x3),x∈(0,π).
-
sec x = ∑ n = 0 ∞ ( − 1 ) n E 2 n x 2 n ( 2 n ) ! = 1 + 1 2 x 2 + 5 24 x 4 + ο ( x 4 ) , x ∈ ( − π 2 , π 2 ) . \begin{aligned}\sec x=\sum_{n=0}^\infty\frac{(-1)^nE_{2n}x^{2n}}{(2n)!}=1+\frac{1}{2}x^2+\frac{5}{24}x^4+\omicron(x^4),x\in(-\frac{\pi}{2},\frac{\pi}{2}).\end{aligned} secx=n=0∑∞(2n)!(−1)nE2nx2n=1+21x2+245x4+ο(x4),x∈(−2π,2π).
其中 E 2 n E_{2n} E2n为 E u l e r Euler Euler数,定义为 E n = { 1 , n = 0. − ∑ k = 0 n − 1 ( − 1 ) k C 2 n 2 k E k , n ≥ 1. E_n= \begin{cases} 1,n=0.\\[2ex] \begin{aligned}-\sum_{k=0}^{n-1}\end{aligned}(-1)^kC_{2n}^{2k}E_k,n\ge1.\\[2ex] \end{cases} En=⎩ ⎨ ⎧1,n=0.−k=0∑n−1(−1)kC2n2kEk,n≥1.
-
csc x = ∑ n = 0 ∞ ( − 1 ) n + 1 2 ( 2 n − 1 − 1 ) B 2 n ( 2 n ) ! x 2 n − 1 = 1 x + 1 6 x + 7 360 x 3 + ο ( x 3 ) , x ∈ ( 0 , π ) . \begin{aligned}\csc x=\sum_{n=0}^\infty\frac{(-1)^{n+1}2(2^{n-1}-1)B_{2n}}{(2n)!}x^{2n-1}=\frac{1}{x}+\frac{1}{6}x+\frac{7}{360}x^3+\omicron(x^3),x\in(0,\pi).\end{aligned} cscx=n=0∑∞(2n)!(−1)n+12(2n−1−1)B2nx2n−1=x1+61x+3607x3+ο(x3),x∈(0,π).
-
sinh x = ∑ n = 0 ∞ x 2 n + 1 ( 2 n + 1 ) ! = x + 1 3 ! x 3 + ο ( x 3 ) , x ∈ ( − ∞ , + ∞ ) . \begin{aligned}\sinh x=\sum_{n=0}^\infty\frac{x^{2n+1}}{(2n+1)!}=x+\frac{1}{3!}x^3+\omicron(x^3),x\in(-\infty,+\infty).\end{aligned} sinhx=n=0∑∞(2n+1)!x2n+1=x+3!1x3+ο(x3),x∈(−∞,+∞).
-
cosh x = ∑ n = 0 ∞ x 2 n ( 2 n ) ! = 1 + 1 2 ! x 2 + 1 4 ! x 4 + ο ( x 4 ) , x ∈ ( − ∞ , + ∞ ) . \begin{aligned}\cosh x=\sum_{n=0}^\infty\frac{x^{2n}}{(2n)!}=1+\frac{1}{2!}x^2+\frac{1}{4!}x^4+\omicron(x^4),x\in(-\infty,+\infty).\end{aligned} coshx=n=0∑∞(2n)!x2n=1+2!1x2+4!1x4+ο(x4),x∈(−∞,+∞).
-
tanh x = ∑ n = 1 ∞ 2 2 n ( 2 2 n − 1 ) B 2 n x 2 n − 1 ( 2 n ) ! = x − 1 3 x 3 + ο ( x 3 ) , x ∈ ( − π 2 , π 2 ) . \begin{aligned}\tanh x=\sum_{n=1}^\infty\frac{2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}=x-\frac{1}{3}x^3+\omicron(x^3),x\in(-\frac{\pi}{2},\frac{\pi}{2}).\end{aligned} tanhx=n=1∑∞(2n)!22n(22n−1)B2nx2n−1=x−31x3+ο(x3),x∈(−2π,2π).
-
coth x = ∑ n = 0 ∞ ( − 1 ) n − 1 2 2 n B n ( 2 n ! ) x 2 n − 1 = 1 x + 1 3 x − 1 45 x 3 + ο ( x 3 ) , x ∈ ( − π , π ) . \begin{aligned}\coth x=\sum_{n=0}^\infty\frac{(-1)^{n-1}2^{2n}B_{n}}{(2n!)}x^{2n-1}=\frac{1}{x}+\frac{1}{3}x-\frac{1}{45}x^3+\omicron(x^3),x\in(-\pi,\pi).\end{aligned} cothx=n=0∑∞(2n!)(−1)n−122nBnx2n−1=x1+31x−451x3+ο(x3),x∈(−π,π).
-
s e c h x = ∑ n = 0 ∞ ( − 1 ) n E 2 n ( 2 n ) ! x 2 n = 1 − 1 2 ! x 2 + 5 4 ! x 4 + ο ( x 4 ) , x ∈ ( − π 2 , π 2 ) . \begin{aligned}\mathrm{sech}\,x=\sum_{n=0}^\infty\frac{(-1)^nE_{2n}}{(2n)!}x^{2n}=1-\frac{1}{2!}x^2+\frac{5}{4!}x^4+\omicron(x^4),x\in(-\frac{\pi}{2},\frac{\pi}{2}).\end{aligned} sechx=n=0∑∞(2n)!(−1)nE2nx2n=1−2!1x2+4!5x4+ο(x4),x∈(−2π,2π).
-
c s c h x = ∑ n = 0 ∞ 2 ( − 1 ) n ( 2 2 n − 1 − 1 ) B n ( 2 n ) ! x 2 n − 1 = 1 x − 1 6 x + 7 360 x 3 + ο ( x 3 ) , x ∈ ( − π , π ) . \begin{aligned}\mathrm{csch}\,x=\sum_{n=0}^\infty\frac{2(-1)^n(2^{2n-1}-1)B_n}{(2n)!}x^{2n-1}=\frac{1}{x}-\frac{1}{6}x+\frac{7}{360}x^3+\omicron(x^3),x\in(-\pi,\pi).\end{aligned} cschx=n=0∑∞(2n)!2(−1)n(22n−1−1)Bnx2n−1=x1−61x+3607x3+ο(x3),x∈(−π,π).
-
a r c s i n h x = ∑ n = 0 ∞ ( ( − 1 ) n ( 2 n ) ! 2 2 n ( n ! ) 2 ) x 2 n + 1 2 n + 1 = x − 1 6 x 3 + ο ( x 3 ) , x ∈ ( − 1 , 1 ) . \begin{aligned}\mathrm{arcsinh}\,x=\sum_{n=0}^\infty\begin{pmatrix}\frac{(-1)^n(2n)!}{2^{2n}(n!)^2}\end{pmatrix}\frac{x^{2n+1}}{2n+1}=x-\frac{1}{6}x^3+\omicron(x^3),x\in(-1,1).\end{aligned} arcsinhx=n=0∑∞(22n(n!)2(−1)n(2n)!)2n+1x2n+1=x−61x3+ο(x3),x∈(−1,1).
-
a r c c o s h x = ln ( 2 x ) − ∑ n = 1 ∞ ( ( − 1 ) n ( 2 n ) ! 2 2 n ( n ! ) 2 ) x − 2 n 2 n = ln ( 2 x ) − 1 4 x − 2 − 3 32 x − 4 + ο ( x − 4 ) , { x ∈ R ∣ x ∉ [ − 1 , 1 ] } . \begin{aligned}\mathrm{arccosh}\,x=\ln(2x)-\sum_{n=1}^\infty\begin{pmatrix}\frac{(-1)^n(2n)!}{2^{2n}(n!)^2}\end{pmatrix}\frac{x^{-2n}}{2n}=\ln(2x)-\frac{1}{4}x^{-2}-\frac{3}{32}x^{-4}+\omicron(x^{-4}),\{x\in \mathbb{R}|x\notin[-1,1]\}.\end{aligned} arccoshx=ln(2x)−n=1∑∞(22n(n!)2(−1)n(2n)!)2nx−2n=ln(2x)−41x−2−323x−4+ο(x−4),{x∈R∣x∈/[−1,1]}.
-
a r c t a n h x = ∑ n = 0 ∞ x 2 n + 1 2 n + 1 = x + 1 3 x 3 + ο ( x 3 ) , x ∈ ( − 1 , 1 ) . \begin{aligned}\mathrm{arctanh}\,x=\sum_{n=0}^\infty\frac{x^{2n+1}}{2n+1}=x+\frac{1}{3}x^3+\omicron(x^3),x\in(-1,1).\end{aligned} arctanhx=n=0∑∞2n+1x2n+1=x+31x3+ο(x3),x∈(−1,1).
a r c c o t h x \mathrm{arccoth}\,x arccothx 、 a r c s e c h x \mathrm{arcsech}\,x arcsechx 和 a r c c s c h x \mathrm{arccsch}\,x arccschx的公式找不到了。
相关文章:

高等数学:泰勒公式
注:第三条 e x e^x ex的展开式,在 1 1 1和 1 2 x 2 \frac{1}{2}x^2 21x2之间添上一个 x x x。 1 1 − x ∑ n 0 ∞ x n 1 x x 2 x 3 ο ( x 3 ) , x ∈ ( − 1 , 1 ) . \begin{aligned}\frac{1}{1-x}\sum_{n0}^\infty x^n1xx^2x^3\omicron(x^…...

JZ32 从上往下打印二叉树(Java)
题目地址:从上往下打印二叉树_牛客题霸_牛客网 题目回顾: 不分行从上往下打印出二叉树的每个节点,同层节点从左至右打印。例如输入{8,6,10,#,#,2,1},如以下图中的示例二叉树,则依次打印8,6,10,2,1(空节点不打印&…...
hackNos靶机
靶机训练1 - hackNos: Os-hackNos 靶机平台 Vulnhub 是一个提供各种漏洞环境的靶场平台,供安全爱好者学习使用,大部分环境是做好的虚拟机镜像文件,镜像预先设计了多种漏洞,需要使用VMware或者VirtualBox运行。每个镜像会有破解的目…...

取地址及 const取地址操作符重载
取地址及 const取地址操作符重载 #include <iostream> using namespace std;class A { public:A(int year, int month, int day){_year year;_month month;_day day;}//它们是默认成员函数,我们不写编译器会自动生成,自动生成就够用了ÿ…...
【Linux初阶】进程间通信介绍 管道
🌟hello,各位读者大大们你们好呀🌟 🍭🍭系列专栏:【Linux初阶】 ✒️✒️本篇内容:进程间通信介绍,管道概述,匿名管道应用,命名管道应用 🚢&#…...

App 在macOS Catalina下提示已损坏无法打开解决办法:
App 在macOS Catalina下提示已损坏无法打开解决办法: 打开终端; 输入以下命令,回车; sudo xattr -d com.apple.quarantine /Applications/xxxx.app注意:/Applications/xxxx.app 换成你的App路径(推荐直接…...

ad+硬件每日学习十个知识点(26)23.8.6 (DCDC的降压电路、升压电路、降压-升压电路,同步整流,选型考虑同步、隔离)
文章目录 1.DCDC的降压原理2.DCDC的升压原理3.DCDC的升压和降压原理4.什么是肖特基二极管造成的死区电压?5.MOS管有死区电压么?6.DCDC的同步整流(用MOS管取代整流二极管,避免死区电压的影响)7.DCDC选型——同步与非同步…...

Elasticsearch3节点集群配置账号密码安全验证
Elasticsearch3节点集群配置账号密码安全验证 ES配置文件 rootnode1:~# grep -Ev "^#|^$" /etc/elasticsearch/elasticsearch.yml cluster.name: es-pre node.name: node1 node.master: true node.data: true path.data: /data/elk/es/data path.logs: /data/elk/…...

ffmepg滤镜
视频按顺时针方向旋转90度 ffplay -vf transpose1 -i juren-30s.mp4 ffplay -f lavfi -i testsrc -vf transpose1 -f lavfi -i testsrc这个滤镜是ffmpeg给用户的一个测试使用的视频 视频水平翻转(左右翻转) -vf hflip 实现慢速播放,声音速度是原始速度的50% ffpla…...
常用命令 - find locate which whereis gzip gunzip tar)
Linux 基础(六)常用命令 - find locate which whereis gzip gunzip tar
find & locate & which & whereis & gzip & gunzip & tar findlocatewhichwhereisgzipgunzipzip/unziptar find 在指定目录下查找文件或目录 find --help Usage: find [-H] [-L] [-P] [-Olevel] [-D help|tree|search|stat|rates|opt|exec] [path...…...

【Ajax】回调地狱解决方法
回调地狱(Callback Hell)是指在异步编程中,特别是在嵌套的回调函数中,代码变得深度嵌套、难以阅读和维护的现象。这通常发生在处理多个异步操作时,每个操作都依赖于前一个操作的结果。回调地狱使代码变得难以理解、扩展…...

解决Vue根组件设置transition失效的问题
解决Vue根组件设置transition失效的问题 1.代码 <div id"app"><!-- :name"$route.meta.transitionName" --><transition :name"animation" mode"out-in"><router-view /></transition></div>&…...

【剑指 Offer 40】最小的k个数
题目: 输入整数数组 arr ,找出其中最小的 k 个数。例如,输入 4、5、1、6、2、7、3、8 这 8 个数字,则最小的 4 个数字是 1、2、3、4。 示例: 输入:arr [3,2,1], k 2 输出:[1,2] 或者 [2,1] …...
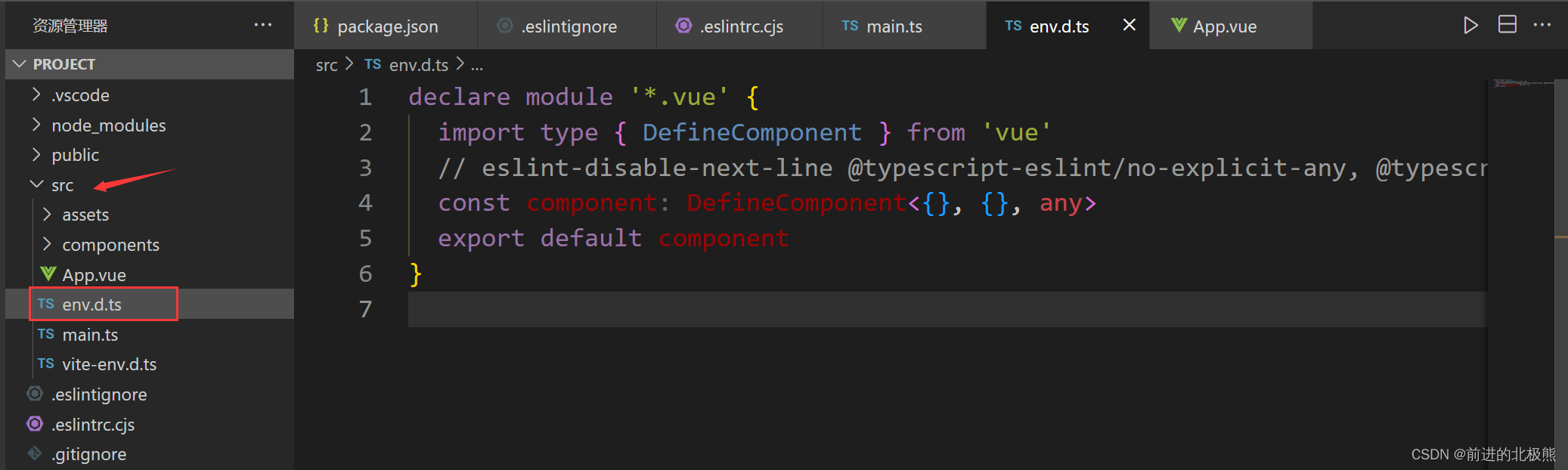
vue3+vite在main.ts文件中引入./App.vue报错(./App.vue不是模块)
问题 如下图: 方法一 下载TypeScript Vue Plugin (Volar)插件就不报红了,看它的描述应该就是ts文件可以识别vue文件。 方法二 在src文件夹下添加env.d.ts文件,添加以下代码: declare module *.vue {import type { DefineC…...

【LeetCode】102. 二叉树的层序遍历、107. 二叉树的层序遍历 II
作者:小卢 专栏:《Leetcode》 喜欢的话:世间因为少年的挺身而出,而更加瑰丽。 ——《人民日报》 102. 二叉树的层序遍历 102. 二叉树的层序遍历 给你二叉树的根节点 root ,返回其节…...

HTML详解连载(2)
HTML详解连载(2) 专栏链接 [link](http://t.csdn.cn/xF0H3)下面进行专栏介绍 开始喽超链接作用代码示例解释经验分享 音频标签代码示例注意强调 视频标签代码示例注意强调 列表作用:布局内容排列整齐的区域。分类:无序列表&#x…...

qt事件系统源码-----定时器
qt定时器的使用一般有以下几种方式: 1、直接使用QTimer对象,绑定定时器的timeout信号; 2、使用QTimer的静态方法singleshot方法,产生一个一次性的定时事件 3、在QObject子类中,调用startTimer方法,产生定…...

【Android】ViewBinding+DataBinding+MVVM新手快速上手
为什么写这篇博客 网上大部分博客,代码量都比较大,把实际的业务都代入进去了 这篇博客的目的,就是为了讲解基本原理和使用思路,然后给出一个最简单的Demo 这里不讲解具体用法,那样篇幅会太长,直接看Demo…...
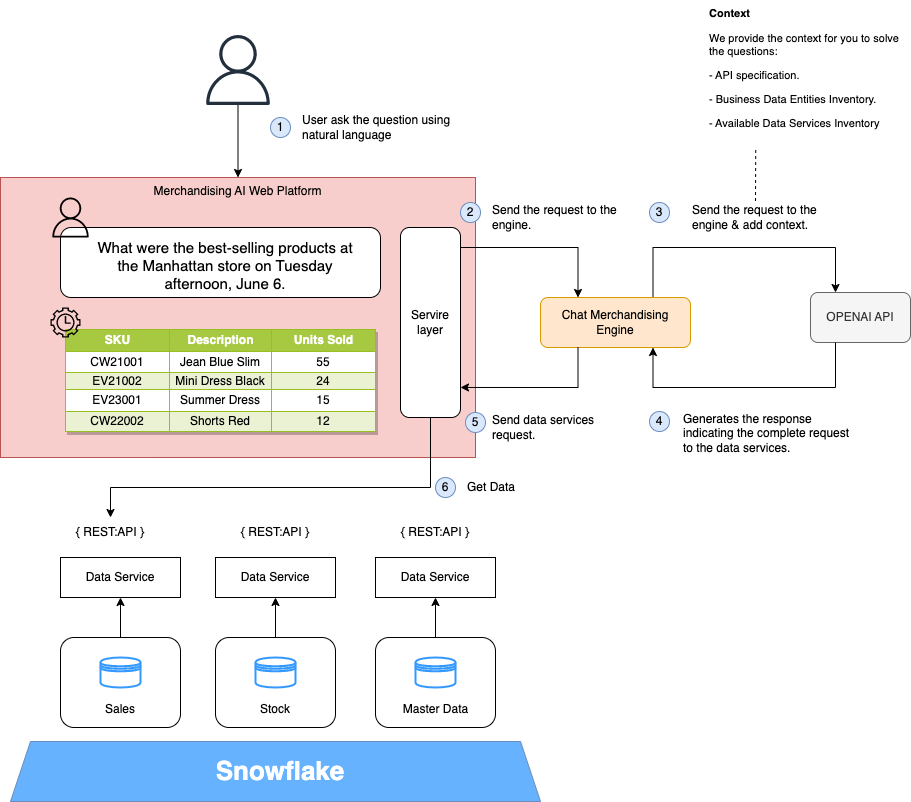
生成式人工智能模型:提升营销分析用户体验
使用生成式人工智能来改善分析体验,使业务用户能够询问有关我们数据平台中可用数据的任何信息。 在本文中,我们将解释如何使用新的生成式人工智能模型 ( LLM ) 来改善业务用户在我们的分析平台上的体验。假设我们为零售销售经理提供 Web 应用程序或移动应…...
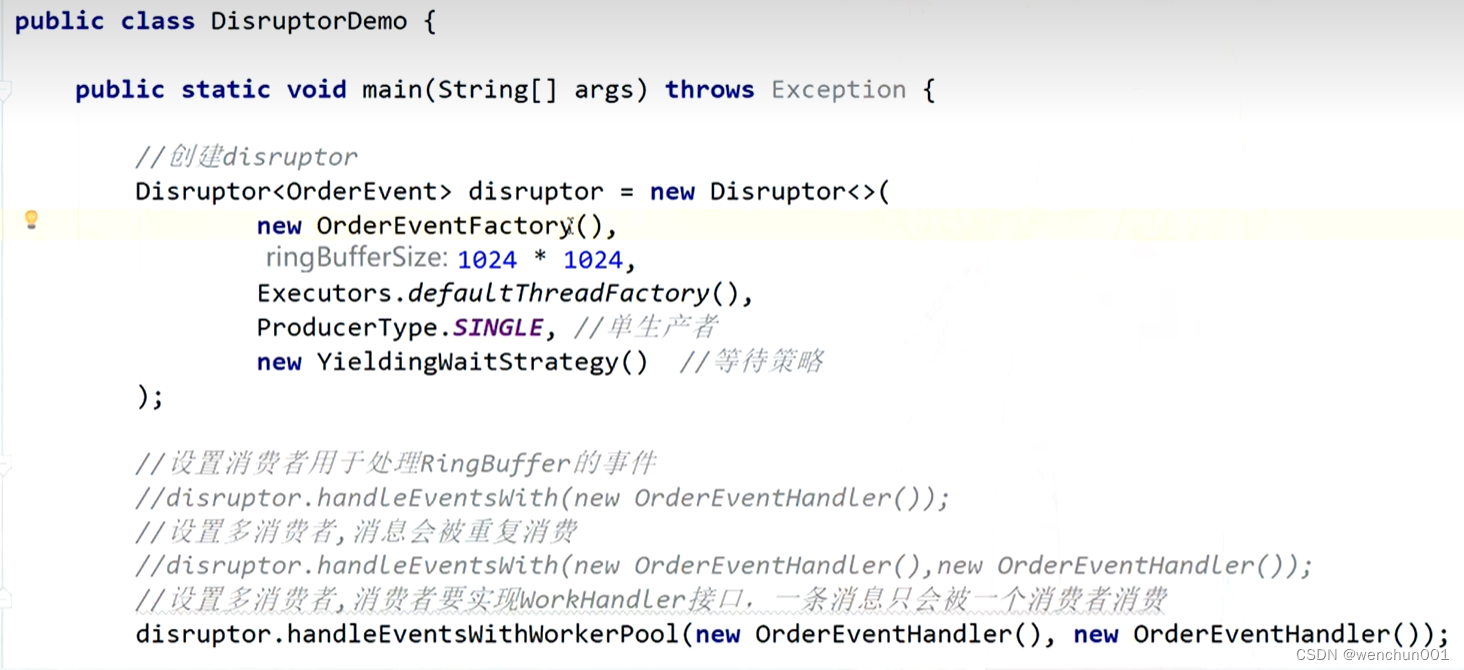
【并发编程】无锁环形队列Disruptor并发框架使用
Disruptor 是苹国外厂本易公司LMAX开发的一个高件能列,研发的初夷是解决内存队列的延识问顾在性能测试中发现竟然与10操作处于同样的数量级),基于Disruptor开发的系统单线程能支撑每秒600万订单,2010年在QCn演讲后,获得了业界关注…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...

13.10 LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析
LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析 LanguageMentor 对话式训练系统架构与实现 关键词:多轮对话系统设计、场景化提示工程、情感识别优化、LangGraph 状态管理、Ollama 私有化部署 1. 对话训练系统技术架构 采用四层架构实现高扩展性的对话训练…...

RKNN开发环境搭建2-RKNN Model Zoo 环境搭建
目录 1.简介2.环境搭建2.1 启动 docker 环境2.2 安装依赖工具2.3 下载 RKNN Model Zoo2.4 RKNN模型转化2.5编译C++1.简介 RKNN Model Zoo基于 RKNPU SDK 工具链开发, 提供了目前主流算法的部署例程. 例程包含导出RKNN模型, 使用 Python API, CAPI 推理 RKNN 模型的流程. 本…...
)
MySQL基本操作(续)
第3章:MySQL基本操作(续) 3.3 表操作 表是关系型数据库中存储数据的基本结构,由行和列组成。在MySQL中,表操作包括创建表、查看表结构、修改表和删除表等。本节将详细介绍这些操作。 3.3.1 创建表 在MySQL中&#…...
华为OD机考- 简单的自动曝光/平均像素
import java.util.Arrays; import java.util.Scanner;public class DemoTest4 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint[] arr Array…...
