解决Vue根组件设置transition失效的问题
解决Vue根组件设置transition失效的问题
1.代码
<div id="app"><!-- :name="$route.meta.transitionName" --><transition :name="'animation'" mode="out-in"><router-view /></transition></div><!-- 动画部分代码省略 -->
这样直接设置会发现路由切换时并没有效果,但是你每次修改代码后保存刷新页面时却又能看到一次动画效果。
2.解决办法
在router-view标签设置 key属性,并且确保是唯一的,这里我设置 :key=“$route.fullPath”
以下为修改后的代码:
<div id="app"><!-- :name="$route.meta.transitionName" --><transition :name="'animation'" mode="out-in"><router-view :key="$route.fullPath" /></transition></div>
修改后,transition动画就正常了。
分析
在 <router-view> 上使用 :key=“$route.fullPath” 时,每当路由发生变化时,$route.fullPath 的值会发生变化,因为它会随着新的路由而更新。
这就意味着,每当路由切换时, 组件的 key 会变化,从而触发 Vue.js 重新渲染组件。
在重新渲染的过程中,过渡效果会应用于离开的旧组件和进入的新组件,从而实现平滑的过渡效果。
相关文章:

解决Vue根组件设置transition失效的问题
解决Vue根组件设置transition失效的问题 1.代码 <div id"app"><!-- :name"$route.meta.transitionName" --><transition :name"animation" mode"out-in"><router-view /></transition></div>&…...

【剑指 Offer 40】最小的k个数
题目: 输入整数数组 arr ,找出其中最小的 k 个数。例如,输入 4、5、1、6、2、7、3、8 这 8 个数字,则最小的 4 个数字是 1、2、3、4。 示例: 输入:arr [3,2,1], k 2 输出:[1,2] 或者 [2,1] …...
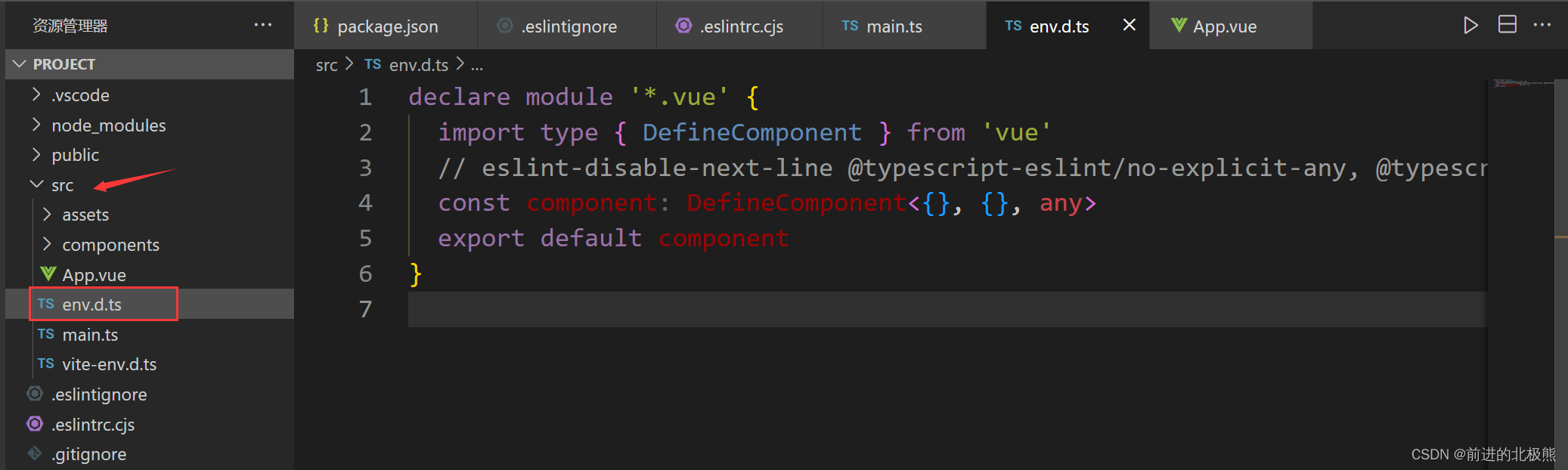
vue3+vite在main.ts文件中引入./App.vue报错(./App.vue不是模块)
问题 如下图: 方法一 下载TypeScript Vue Plugin (Volar)插件就不报红了,看它的描述应该就是ts文件可以识别vue文件。 方法二 在src文件夹下添加env.d.ts文件,添加以下代码: declare module *.vue {import type { DefineC…...

【LeetCode】102. 二叉树的层序遍历、107. 二叉树的层序遍历 II
作者:小卢 专栏:《Leetcode》 喜欢的话:世间因为少年的挺身而出,而更加瑰丽。 ——《人民日报》 102. 二叉树的层序遍历 102. 二叉树的层序遍历 给你二叉树的根节点 root ,返回其节…...

HTML详解连载(2)
HTML详解连载(2) 专栏链接 [link](http://t.csdn.cn/xF0H3)下面进行专栏介绍 开始喽超链接作用代码示例解释经验分享 音频标签代码示例注意强调 视频标签代码示例注意强调 列表作用:布局内容排列整齐的区域。分类:无序列表&#x…...

qt事件系统源码-----定时器
qt定时器的使用一般有以下几种方式: 1、直接使用QTimer对象,绑定定时器的timeout信号; 2、使用QTimer的静态方法singleshot方法,产生一个一次性的定时事件 3、在QObject子类中,调用startTimer方法,产生定…...

【Android】ViewBinding+DataBinding+MVVM新手快速上手
为什么写这篇博客 网上大部分博客,代码量都比较大,把实际的业务都代入进去了 这篇博客的目的,就是为了讲解基本原理和使用思路,然后给出一个最简单的Demo 这里不讲解具体用法,那样篇幅会太长,直接看Demo…...
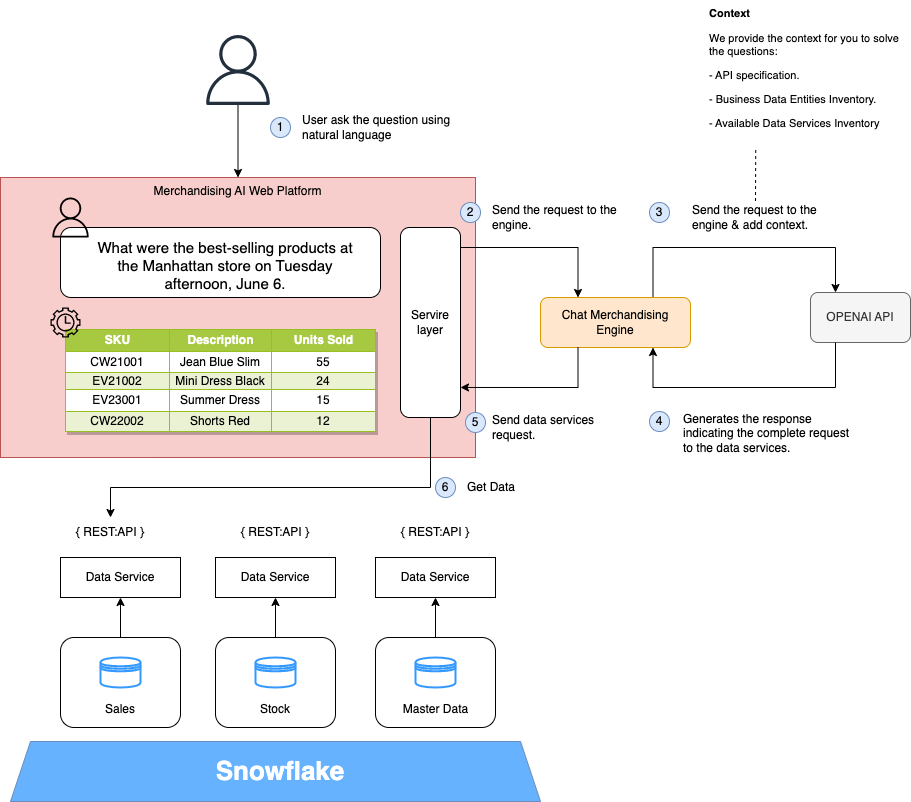
生成式人工智能模型:提升营销分析用户体验
使用生成式人工智能来改善分析体验,使业务用户能够询问有关我们数据平台中可用数据的任何信息。 在本文中,我们将解释如何使用新的生成式人工智能模型 ( LLM ) 来改善业务用户在我们的分析平台上的体验。假设我们为零售销售经理提供 Web 应用程序或移动应…...
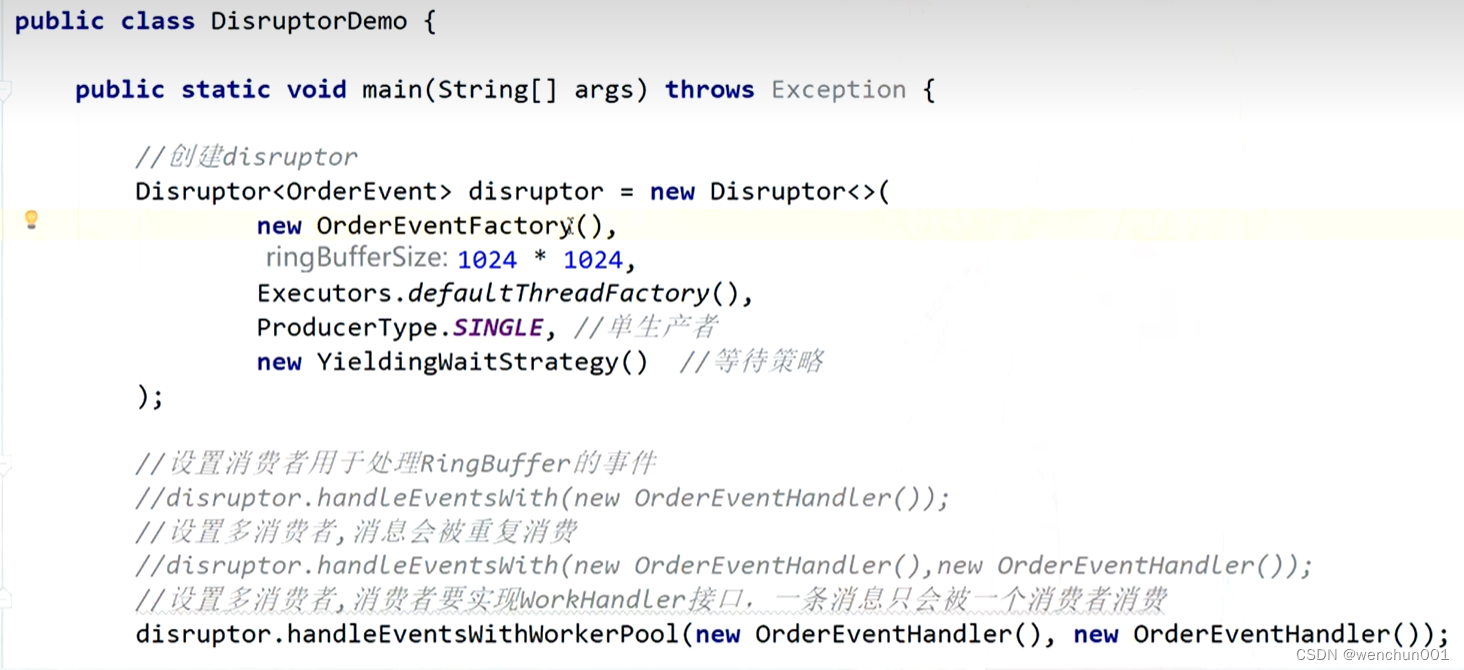
【并发编程】无锁环形队列Disruptor并发框架使用
Disruptor 是苹国外厂本易公司LMAX开发的一个高件能列,研发的初夷是解决内存队列的延识问顾在性能测试中发现竟然与10操作处于同样的数量级),基于Disruptor开发的系统单线程能支撑每秒600万订单,2010年在QCn演讲后,获得了业界关注…...

【C语言】初阶指针详解
大家好,我是苏貝,本篇博客带大家了解C语言中令人头疼的指针,如果大家觉得我写的不错的话,可以给我一个赞👍吗,感谢❤️ 使用的是VS2019编译器,默认为32位平台 文章目录 ①指针是什么②指针定义与…...
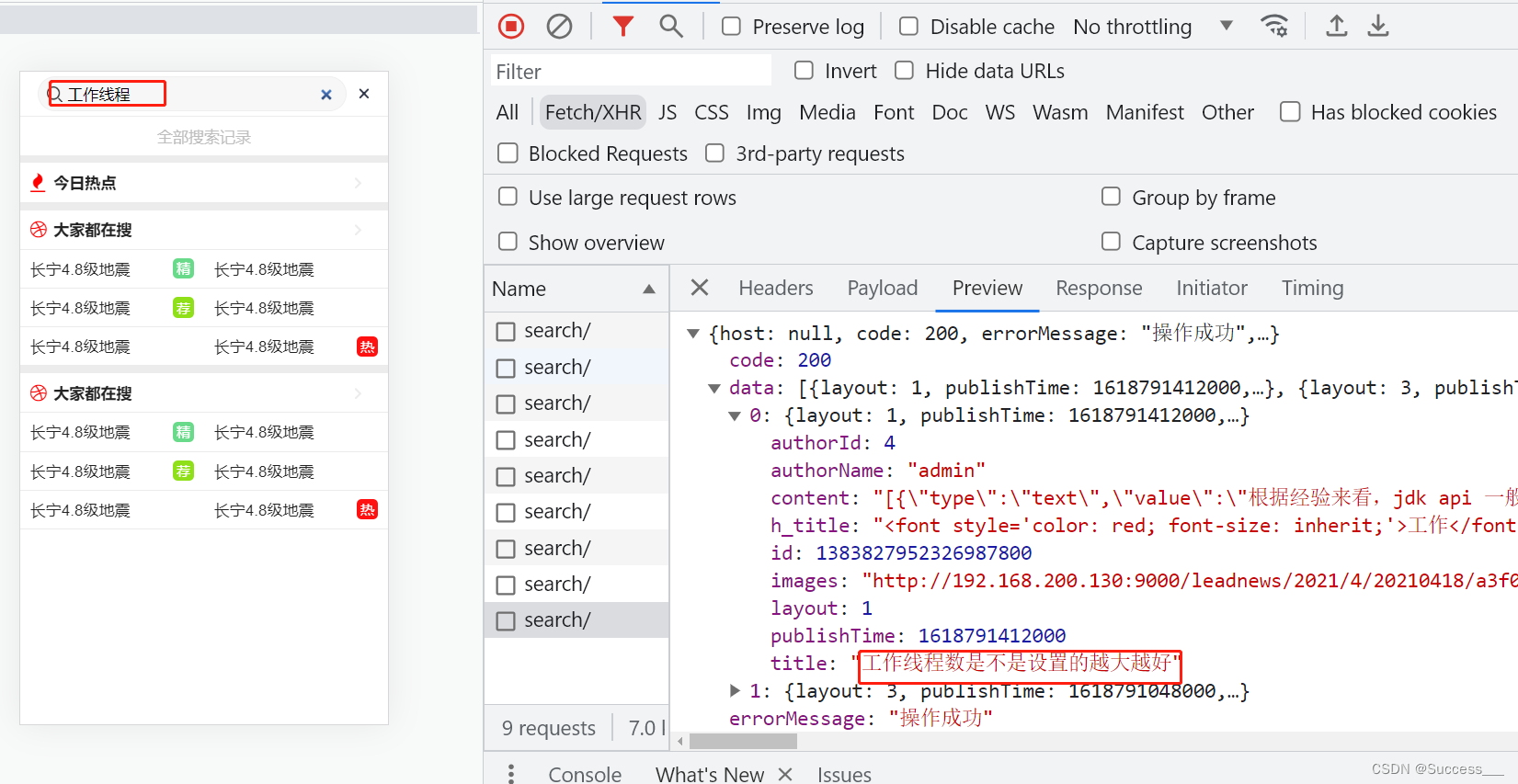
ElasticSearch:项目实战(1)
es环境搭建参考:ElasticSearch:环境搭建步骤_Success___的博客-CSDN博客 需求: 用户输入关键可搜索文章列表 关键词高亮显示 文章列表展示与home展示一样,当用户点击某一篇文章,可查看文章详情 思路: …...

React 实现文件分片上传和下载
React 实现文件分片上传和下载 在开发中,文件的上传和下载是常见的需求。然而,当面对大型文件时,直接的上传和下载方式可能会遇到一些问题,比如网络传输不稳定、文件过大导致传输时间过长等等。为了解决这些问题,我们…...

2023.8.13
atcoder_abc\AtCoder Beginner Contest 310\E_NAND_repeatedly //题意:给定一个n长度的01串,计算f(l,r)(l<r,l在1~n,r在1~n)的和,f的计算(ai,a(i1))运算,有0就为1,11为0 //若f(l,r)1,则f(l,r-1)为0或sr为0,即只取决于上一位的情况和当前位ÿ…...

kvm not all arguments converted during string
kylin virt-manager 远程镜像制作问题记录(not all arguments ) 项目场景: 服务器端安装的OS版本:Kylin-Server-10-SP1-Release-Build20-20210518-arm64-2021-05-18 客户端安装的OS版本:Kylin-Server-10-SP1-Release-Build20-20210518-x86_…...

JVM 基础
巩固基础,砥砺前行 。 只有不断重复,才能做到超越自己。 能坚持把简单的事情做到极致,也是不容易的。 JVM 类加载机制 JVM 类加载机制分为五个部分:加载,验证,准备,解析,初始化&am…...

智谷星图赵俊:让人才和区块链产业“双向奔赴”丨对话MVP
区块链产业需要什么样的人才?赵俊很有发言权。 赵俊是北京智谷星图科技有限公司的技术总监,也是FISCO BCOS官方认证讲师。他2017年接触区块链,随后选择人才培育领域深耕。“为区块链行业引进更多人才这件事很有价值,跟我的职业理…...
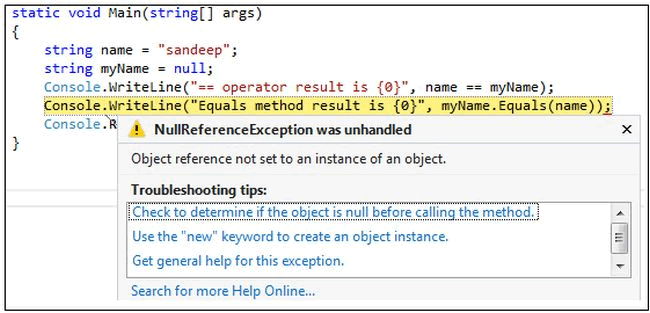
C# Equals()方法报错:NullReferenceException was unhandled
下面是一个C# Equals()方法的例子,执行时报错了 static void Main(string[] args) {string name "sandeep";string myName null;Console.WriteLine(" operator result is {0}", name myName);Console.WriteLine("Equals method result…...
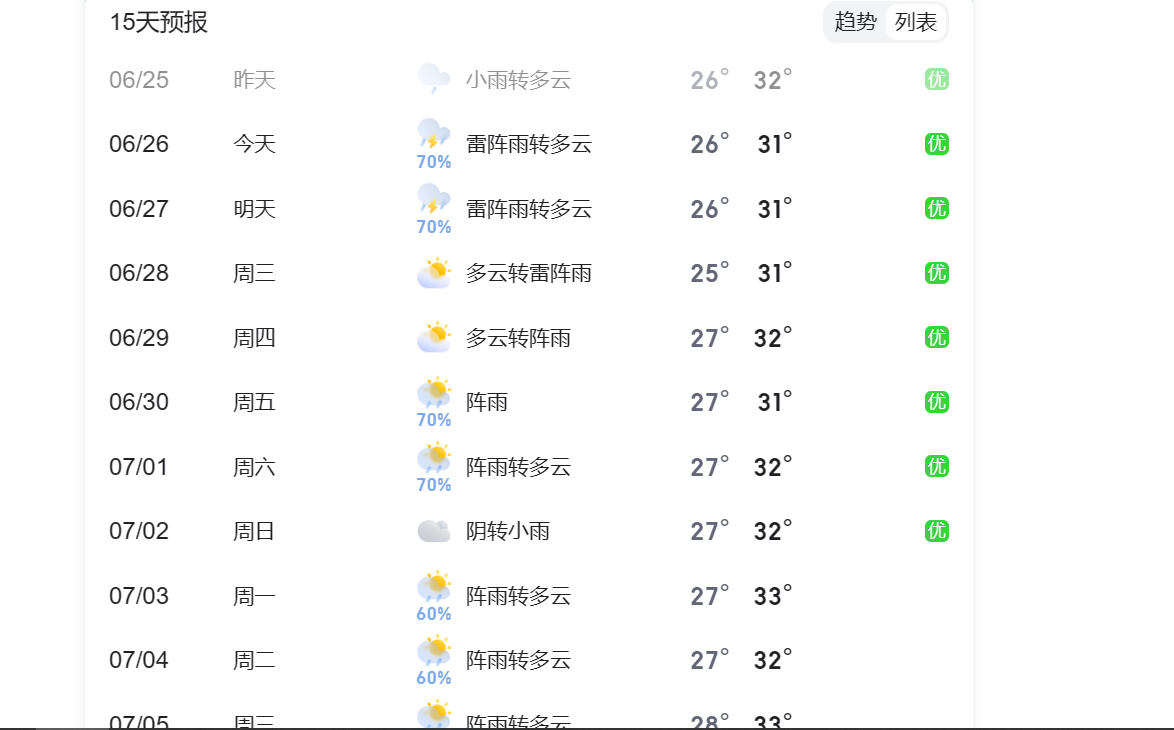
Linux下C语言调用libcurl库获取天气预报信息
一、概述 当前文章介绍如何在Linux(Ubuntu)下使用C语言调用libcurl库获取天气预报的方法。通过HTTP GET请求访问百度天气API,并解析返回的JSON数据,可以获取指定城市未来7天的天气预报信息。 二、设计思路 【1】使用libcurl库进…...

“深入解析JVM:Java虚拟机原理和内部结构“
标题:深入解析JVM:Java虚拟机原理和内部结构 摘要:本文将深入解析JVM(Java虚拟机)的原理和内部结构。我们将从JVM的基础概念开始,逐步介绍其组成部分,包括类加载器、运行时数据区、字节码解释器…...
 返回的list不能add,remove)
Arrays.asList() 返回的list不能add,remove
一.Arrays.asList() 返回的list不能add,remove Arrays.asList()返回的是List,而且是一个定长的List,所以不能转换为ArrayList,只能转换为AbstractList 原因在于asList()方法返回的是某个数组的列表形式,返回的列表只是数组的另一个视图,而数组本身并没…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

python基础语法Ⅰ
python基础语法Ⅰ 常量和表达式变量是什么变量的语法1.定义变量使用变量 变量的类型1.整数2.浮点数(小数)3.字符串4.布尔5.其他 动态类型特征注释注释是什么注释的语法1.行注释2.文档字符串 注释的规范 常量和表达式 我们可以把python当作一个计算器,来进行一些算术…...
