图论——最短路算法
引入:
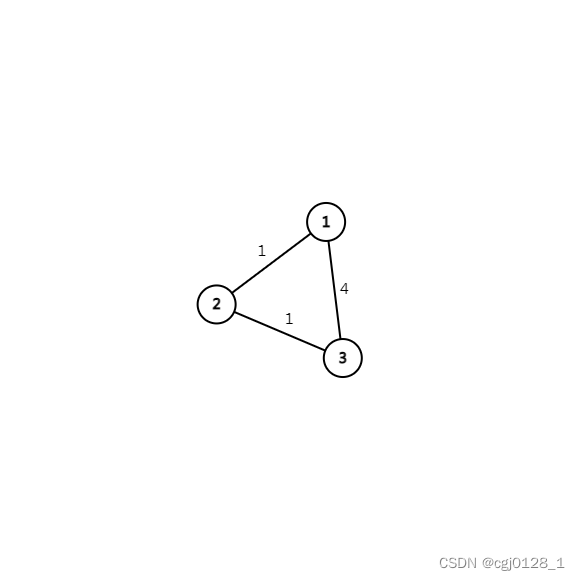
如上图,已知图G。
问节点1到节点3的最短距离。
可心算而出为d[1,2]+d[2,3]=1+1=2,比d[1,3]要小。
求最短路径算法:
1.Floyd(弗洛伊德)
是一种基于三角形不等式的多源最短路径算法。边权可以为负数
表现为a[i,j]+a[j,k]<a[i,k]。
算法思想:
枚举“中转站”(k),“起点”(i),“终点”(j)
设d[i,j]为由i点到j点的最短路径
则
初始化d[i,j]为无穷大 ()
算法模板如下:
inline int Floyd(int n,int st,int ed)// n个点,起点st,终点ed,返回st到ed的最短距离
{int d[n][n];memset(d,0x3f,sizeof(d));for(int i=1;i<=n;i++) d[i][i]=0;for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){d[i][j]=min(d[i][j],d[i][k]+d[k][j]);}}}return d[st][ed];
}补充:Floyd输出最短路径。
题目:有向图中任意两点最短路径(floyd)
题目描述
一个含n个结点的有向图(注意:是有向图!!),以矩阵存储方式给出,请求出指定的多组两个点之间的最短距离及其最短路径。
输入输出格式
输入格式:
第1行,一个整数n(0 < n < 300 ),表示有向图中结点的个数。
第2行到第(n+1)行,是一个n*n的矩阵,表示无向图中各结点之间的联结情况,矩阵中的数据为小于1000的正整数,其中 -1 表示无穷大!!
第(n+2)行,一个整数m,表示接下来有m组顶点 < i , j >对 ,其中,i是起点,j是终点,且i不等于j。
接下来有m行,每行两个整数,中间一个空格间隔,分别表示i和j,表示求解i点到j点的最短距离及最短路径。
注:输入数据已经确保答案每一组顶点间的最短路径是唯一的,无多解数据存在,顶点编号用数字表示,从1开始编号,至n结束!
输出格式:
共 2m 行。
第(m-1)*2+1行,一个整数,表示第m组顶点的最短距离,若两点间距离为无穷大,则输出 -1。
第(m-1)*2+2行,用顶点编号表示的路径序列,各顶点编号间用一个空格间隔,表示第m组顶点的最短路径,若两点间距离为无穷大,则输出的路径序列为 -1。
输入输出样例
输入样例#1:
3
0 4 11
6 0 2
3 -1 0
2
2 1
3 2
输出样例#1:
5
2 3 1
7
3 1 2
代码如下:
#include<bits/stdc++.h>
using namespace std;
int n,q;
int d[10001][10001],pre[10001][10001];
void dg(int i,int j)
{if(i==j||pre[i][j]==0) return;int k=pre[i][j];dg(i,k);dg(k,j);
}
int main()
{cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>d[i][j];if(d[i][j]==-1){d[i][j]=0x7fffff;}}}for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(d[i][k]+d[k][j]<d[i][j]){d[i][j]=d[i][k]+d[k][j];pre[i][j]=k;}}}}cin>>q;for(int i=1;i<=q;i++){int x,y;cin>>x>>y;cout<<d[x][y]<<endl;cout<<x<<" ";dg(x,y);cout<<y;cout<<endl;}return 0;
}传递闭包(连通性)
d[i,j]表示i与j是否连通。
题目:刻录光盘
题目描述
在FJOI2010夏令营快要结束的时候,很多营员提出来要把整个夏令营期间的资料刻录成一张光盘给大家,以便大家回去后继续学习。组委会觉得这个主意不错!可是组委会一时没有足够的空光盘,没法保证每个人都能拿到刻录上资料的光盘,怎么办呢?!
DYJ分析了一下所有营员的地域关系,发现有些营员是一个城市的,其实他们只需要一张就可以了,因为一个人拿到光盘后,其他人可以带着U盘之类的东西去拷贝啊!
他们愿意某一些人到他那儿拷贝资料,当然也可能不愿意让另外一些人到他那儿拷贝资料,这与我们FJOI宣扬的团队合作精神格格不入!!!
现在假设总共有N个营员(2<=N<=200),每个营员的编号为1~N。DYJ给每个人发了一张调查表,让每个营员填上自己愿意让哪些人到他那儿拷贝资料。当然,如果A愿意把资料拷贝给B,而B又愿意把资料拷贝给C,则一旦A获得了资料,则B,C都会获得资料。
现在,请你编写一个程序,根据回收上来的调查表,帮助DYJ计算出组委会至少要刻录多少张光盘,才能保证所有营员回去后都能得到夏令营资料?
输入输出格式
输入格式:
先是一个数N,接下来的N行,分别表示各个营员愿意把自己获得的资料拷贝给其他哪些营员。即输入数据的第i+1行表示第i个营员愿意把资料拷贝给那些营员的编号,以一个0结束。如果一个营员不愿意拷贝资料给任何人,则相应的行只有1个0,一行中的若干数之间用一个空格隔开。
输出格式:
一个正整数,表示最少要刻录的光盘数。
输入输出样例
输入样例#1:
5
2 4 3 0
4 5 0
0
0
1 0
输出样例#1:
1
代码:
#include<bits/stdc++.h>
using namespace std;
int f[100001],d[300][300],g[100001],ans;
int main()
{int n;cin>>n;memset(d,0x3f,sizeof(d));for(int i=1;i<=n;i++){f[i]=i;}for(int i=1;i<=n;i++){int x;while(1){cin>>x;if(x==0) break;d[i][x]=1;}}for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(i!=j&&j!=k&&k!=i){if(d[i][k]==1&&d[k][j]==1){d[i][j]=1;}}}}}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(d[i][j]==1){f[j]=f[i];}}}for(int i=1;i<=n;i++) {if(f[i]==i) {ans++;}}cout<<ans;return 0;
} 2.dijkstra(狄克斯特拉,迪杰斯特拉)
基于贪心的单源最短路径算法。边权必须为正数
基本思想:
设d[i]为起点s到终点i的最短路径,a[i,j]为点i到点j边权。
1.找 ,并将其用k记录
2.
3. 松弛操作,用k来更新图中所有点。
int dijkstra(int n,int st,int ed)
{int dis[n+1],vis[n+1];memset(dis,0x3f,sizeof(dis));memset(vis,0,sizeof(vis));dis[st]=0;for(int i=1;i<=n;i++){int k,minn=0x7fffff;for(int j=1;j<=n;j++)if(!vis[j]&&dis[j]<minn) minn=dis[j],k=j;vis[k]=true;for(int j=1;j<=n;j++) d[j]=min(d[j],d[k]+a[k][j]);}return d[ed];
}堆优化dijkstra:
typedef pair<int,int> P;
struct node{int to;int next;int w;
}edge[10000010];
int head[10000010],d[10000010];
int cnt;
int n,m,x,y,z,s;
void add_edge(int u,int v,int w)
{edge[cnt].to=v;edge[cnt].w=w;edge[cnt].next=head[u];head[u]=cnt++;
}
void dijkstra(int s)
{priority_queue< P,vector<P>,greater<P> >q;memset(d,0x3f,sizeof(d));d[s]=0;q.push(P(0,s));while(!q.empty()){P p=q.top();q.pop();int u=p.second;if(d[u]<p.first) continue;for(int i=head[u];i!=-1;i=edge[i].next){int v=edge[i].to;if(d[v]>d[u]+edge[i].w){d[v]=d[u]+edge[i].w;q.push(P(d[v],v));}}}
}3.Bellman-Ford
O(n*m) 但有更优的,由其转换而来的Spfa算法,不再赘述。边权可以为负数
4.Spfa
基于bellman-Ford,用队列优化的单源最短路径算法,边权可以为负数,可用于判断负环。
代码如下:
int head=0,tail=1;team[1]=s,vis[s]=1,dis[s]=0;while(head<tail){head=(head+1)%10000;int u=team[head];vis[u]=0;for(int i=1;i<=len[u];i++){int v=le[u][i];if(dis[v]>dis[u]+a[u][v]){dis[v]=dis[u]+a[u][v];if(vis[v]==0){tail=(tail+1)%10000;team[tail]=v;vis[v]=1;}}}}相关文章:
图论——最短路算法
引入: 如上图,已知图G。 问节点1到节点3的最短距离。 可心算而出为d[1,2]d[2,3]112,比d[1,3]要小。 求最短路径算法: 1.Floyd(弗洛伊德) 是一种基于三角形不等式的多源最短路径算法。边权可以为负数 表现为a[i,j]a[j,k]<a[i,k]。 …...

在项目中增加网络加载需要考虑什么?
1、下载器 网络加载的第一步肯定是下载,那么选择一个合适的下载器是十分重要的,这个下载器最好支持什么功能? 多线程下载(同时需要服务端支持,下载时可指定range) 断点续传 通用性(其他位置也…...
阿里云服务器部署RabbitMQ流程
阿里云百科分享使用阿里云服务器部署RabbitMQ流程,RabbitMQ是实现了高级消息队列协议(AMQP)的开源消息代理软件,用于在分布式系统中存储转发消息,有良好的易用性、扩展性和高可用性。本文介绍如何通过ECS实例部署Rabbi…...

青大数据结构【2014】
一、单选 二、简答 为了解决顺序队列的假溢出问题,提出了循环队列,即把存储队列的表从逻辑上看成一个环 判别队列空和满有三种方法: 1)采用计数器判别,空时,计数器为0;满时,计数器…...
Ansible Playbook快速部署一主多从MySQL集群
部署目标: 1、快速部署一套一主两从的mysql集群 2、部署过程中支持交互式定义安装目录及监听端口号 部署清单目录结构: rootmaster:/opt/mysql# tree . . ├── group_vars │ └── all.yml ├── hosts ├── mysql.yml └── roles└── mys…...

27.Netty源码之FastThreadLocal
highlight: arduino-light FastThreadLocal FastThreadLocal 的实现与 ThreadLocal 非常类似,Netty 为 FastThreadLocal 量身打造了 FastThreadLocalThread 和 InternalThreadLocalMap 两个重要的类。下面我们看下这两个类是如何实现的。 FastThreadLocalThread 是对…...

linux下离线安装docker
linux下离线安装docker 一、安装docker Docker 官网离线安装文档 https://docs.docker.com/engine/install/binaries/ 整理步骤如下: 官网下载 docker 安装包,地址为 https://download.docker.com/linux/static/stable/,如果是x86就选择x…...
SQL server 异地备份数据库
异地备份数据库 1.备份服务器中设置共享文件夹 2.源服务器数据库中添加异地备份代理作业 EXEC sp_configure show advanced options, 1;RECONFIGURE; EXEC sp_configure xp_cmdshell, 1;RECONFIGURE; declare machine nvarchar(50) 192.168.11.10 --服务器IP declare pa…...
高并发系统设计要点
在系统设计时,如果能预先看到一些问题,并在设计层面提前解决,就会给后期的开发带来很大的便捷。相反,有缺陷的架构设计可能会导致后期的开发工作十分艰难,甚至会造成“推倒重来”的情形。因此,在系统设计阶…...

Redis 拒绝服务漏洞(CVE-2023-28856)修复处理
一、漏洞描述 Redis Labs Redis是美国Redis Labs公司的一套开源的使用ANSI C编写、支持网络、可基于内存亦可持久化的日志型、键值(Key-Value)存储数据库,并提供多种语言的API。 Redis 7.0.0 到 7.0.10版本、6.2.0 到 6.2.11版本、6.0.0 到 …...

Android保存网页的方法
首先要使用js交互就需要懂原理: 感谢大佬:js中document节点获取页面元素的六种方式 1.querySelector()方法 描述:本方法用于根据给定的选择器选中页面元素 如果有多个元素满足条件,则返回第一个满足条件的元素节点 语法ÿ…...

P2P 网络,PING程序。
没有废话,直接上版本号和代码,以及讲解。 crate版本号libp2p0.52.1tokio1.30.0依赖配置: [dependencies] tokio = { version="1.30.0", features=["full"] } libp2p = { version="0.52.1", features=["tokio","dns", &q…...

OPENCV C++(十二)模板匹配
正常模板匹配函数 matchTemplate(img, templatee, resultMat, 0);//模板匹配 这里0代表的是方法,一般默认为0就ok img是输入图像 templatee是模板 resultmat是输出 1、cv::TM_SQDIFF:该方法使用平方差进行匹配,因此最佳的匹配结果在结果为…...

【配置环境】Linux下安装MySQL
目录 一,环境 二,安装步骤 1.使用包管理器安装MySQL 2.配置MySQL的安全选项 3.设置root用户使用密码进行身份验证(可选) 三,拓展知识 1.如何修改MySQL的密码策略? 一,环境 VMware Workst…...
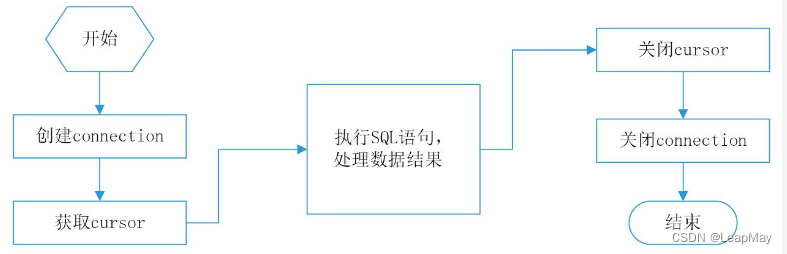
【100天精通python】Day30:使用python操作数据库_数据库基础入门
专栏导读 专栏订阅地址:https://blog.csdn.net/qq_35831906/category_12375510.html 1 数据库基础知识介绍 1.1 什么是数据库? 数据库是一个结构化存储和组织数据的集合,它可以被有效地访问、管理和更新。数据库的目的是为了提供一种可靠的…...

android 如何分析应用的内存(十八)终章——使用Perfetto查看内存与调用栈之间的泄露
android 如何分析应用的内存(十八) 在前面两篇文章中,先是介绍了如何用AS查看Android的堆内存,然后介绍了使用MAT查看 Android的堆内存。AS能够满足基本的内存分析需求,但是无法进行多个堆的综合比较,因此…...

arcpy实现kml批量转出为shp 包括shp合并
参考文章 arcpy实现 kml批量转出为shp_kml批量合并转shp_A873054267的博客-CSDN博客 参考帮助是arcgis里边自带的KMLToLayer_conversion函数 应用场景: 两步路产生的多个轨迹文件KML,批量转换成arcgis 的gdb数据库 最后合并成一个shp 第一步&#…...

高等数学:泰勒公式
注:第三条 e x e^x ex的展开式,在 1 1 1和 1 2 x 2 \frac{1}{2}x^2 21x2之间添上一个 x x x。 1 1 − x ∑ n 0 ∞ x n 1 x x 2 x 3 ο ( x 3 ) , x ∈ ( − 1 , 1 ) . \begin{aligned}\frac{1}{1-x}\sum_{n0}^\infty x^n1xx^2x^3\omicron(x^…...

JZ32 从上往下打印二叉树(Java)
题目地址:从上往下打印二叉树_牛客题霸_牛客网 题目回顾: 不分行从上往下打印出二叉树的每个节点,同层节点从左至右打印。例如输入{8,6,10,#,#,2,1},如以下图中的示例二叉树,则依次打印8,6,10,2,1(空节点不打印&…...
hackNos靶机
靶机训练1 - hackNos: Os-hackNos 靶机平台 Vulnhub 是一个提供各种漏洞环境的靶场平台,供安全爱好者学习使用,大部分环境是做好的虚拟机镜像文件,镜像预先设计了多种漏洞,需要使用VMware或者VirtualBox运行。每个镜像会有破解的目…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...
