(杭电多校)2023“钉耙编程”中国大学生算法设计超级联赛(7)
1002 Random Nim Game
只有3种情况,要么必赢,要么必输,要么从宏观角度考虑,随机的话,赢的概率就是1/2(就像抛硬币一样,随着抛的次数越来越多,正反面的概率将越来越接近1)
当只要有一堆石头数量不是1,那么就是必赢或必输,赢的概率就是1/2
当每堆石头数量都为1时,当堆数为奇数时,先手必赢,概率为1,当堆数为偶数时,先手必输,概率为0
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
const int N=1e5+10,mod=998244353;
int a[N];
int n;
int qmi(int a,int k){int res=1;while(k){if(k&1) res=(ll)res*a%mod;a=(ll)a*a%mod;k>>=1;}return res;
}
void solve()
{cin>>n;for(int i=1;i<=n;i++) cin>>a[i];bool flag=true;for(int i=1;i<=n;i++){if(a[i]!=1){flag=false;break;}}if(!flag) cout<<qmi(2,mod-2)%mod<<endl;else if(n%2==1) cout<<1<<endl;else cout<<0<<endl;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--)solve();return 0;
}1004 Medians Strike Back
参考题解 | #1004.Medians Strike Back# 2023杭电暑期多校7_深翼不通四书五经的博客-CSDN博客
在序列A中选择一个连续序列B,序列B有一个中位数,然后cnt为该中位数在序列B中出现的次数
然后任意选择连续序列B,每一个序列B都有一个cnt,我们取所有连续子序列B的最大的cnt,即为maxn
现构造一个序列A(长度为n,值的范围在[1,3]),使得其maxn最小,输出最小的maxn
首先,我们输出的是次数,所以我们可以选择一个数作为稳定的中位数,专门输出它出现的次数,选择2是比较好的,2本来就是中间数
我们发现当序列中存在两个及以上的2时,我们可以使得2作为稳定的中位数,即131313..22131313...
然后我们考虑这样构造序列:
131313...(x对13)22131313...(x对13)22131313...(x对13)221313...(不足一个周期也没关系)
这样的话,就是131313...(x对13)22,以2*x+2个数字为一周期
为什么可以这样构造呢?
首先,对于整个序列,以2为中位数,所以cnt为整个序列的2的个数sum
然后,对于含有多个2的子序列,2为稳定的中位数,cnt为该子序列中的2的个数,肯定是小于sum的
对于只含有一个2的长度为奇数的子序列,2为稳定的中位数,cnt为该子序列中的2的个数,肯定是小于sum的
对于只含有一个2的长度为偶数的子序列以及不含2的子序列,2将不是中位数,1成为了中位数,cnt即为该子序列中1的个数
首先其它情况中位数的个数都小于sum,所以sum作为预选答案
我们来想一想,我们要保证x刚好等于sum
为什么呢?因为对于一个以1为中位数的子序列,比如说就是131313...(x对13),中位数为1,然后1的个数为x,我们不能让x超过sum,因为我们要最小的最大次数,如果x超过了sum,那么答案就为x了,其次,我们又不能让x小于sum,x太小的话,一个周期的长度2*x+2就太小了,那么2的个数就多了,sum就大了,所以让x刚好等于sum为最优
那么如何使得x刚好等于sum,使用二分来确定,然后答案即为x(x和sum相等)
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<deque>
#include<cmath>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
int n;
void solve() {cin>>n;int l=1,r=n;while(l<r){int mid=(l+r)/2;//mid即为我们要找的xint len=mid*2+2;//一个周期的长度int circle=n/len;//当x为mid时,一个周期的长度为mid*2+2,circle即为最多有几个这样的周期int sum;//sum即为整个序列的2的个数if(n%len<=mid*2) sum=circle*2;//当最后一个周期长度小于等于mid*2时,2的个数即为circle*2else sum=circle*2+len-n%len;//当最后一个周期长度大于mid*2时,那么2的个数即为//如果整个序列的2的个数小于等于x,那么我们寻找更小的xif(sum<=mid) r=mid;//否则说明x太小了else l=mid+1;//反正最终我们要使得sum和x相等}cout<<l<<endl;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--)solve();return 0;
}
1011 Three Operations
三种操作
a,b有可能很大很大,所以(x+a)/2和sqrt(x+b)有可能得到的结果大于等于x,当出现这种情况时,我们就没必要执行这两种操作了,就只需要一直执行x-=1就行了,但是因为数很大,所以一直执行x-=1会超时,所以我们直接返回res+x即可
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
ll x,a,b;
ll solve()
{cin>>x>>a>>b;ll res=0;while(x){if((x+a)/2>=x&&sqrt(x+b)>=x) return res+x;else x=min((x+a)/2,(ll)sqrt(x+b));res++;}return res;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--)cout<<solve()<<endl;return 0;
}1013 M.Minimal and Maximal XOR Sum
算异或后的最小代价,利用归并排序算逆序对,算一共有几对逆序对,每个逆序对倒转的代价为2,然后就是算逆序对数量是奇还是偶,如果是偶数的话,异或后全部抵消了,就变成了0,如果是奇数的话,异或后还剩下一个2,此为异或后的最小值
在这个基础上,比如说最小代价为0,二进制为00或者最小代价为2,二进制为10
首先可以与1异或,即对一个数进行翻转,也就是加1(这是肯定可以操作的,因为最小代价要么为0要么为2,转化为二进制的最后一位肯定是0)
然后最后两位已经定下来了,比如说最小代价为00,与1异或后为01,最小代价为10,与1异或后为11
然后异或的话是二进制数之间按位异或,所以我们看能否使得第三位变为1(从右往左数第三位),比如说最后两位已经确定为11(接下来所说的都是基于这个例子),然后我们看能否使其变成111,也就是在刚才的基础上能否异或一个4
对于已经升序排好的4个数,我们先两两逆序对互换使得其降序,由于4是2的次幂,逆序对的数量肯定是偶数,所以异或和可以全部抵消掉,然后再翻转4个数,即异或一个4,由此,就成功变成了111
然后基于贪心策略,我们不满足于此,我们又希望继续变成1111,即在刚才的基础上异或一个8,同理,只要n的数量大于等于8,我们就可以成功异或一个8,以此类推,看能否异或一个2的次幂
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
const int N=1e5+10;
int a[N],b[N];
int n;
int minn,maxn;
ll res;
void mergesort(int l,int r){if(l==r) return;int mid=(l+r)/2;mergesort(l,mid),mergesort(mid+1,r);int i=l,j=mid+1,k=0;while(i<=mid&&j<=r){if(a[i]<=a[j]) b[k++]=a[i++];else{b[k++]=a[j++];res+=mid-i+1;}}while(i<=mid) b[k++]=a[i++];while(j<=r) b[k++]=a[j++];for(int i=l,j=0;i<=r;i++) a[i]=b[j++];
}
void solve()
{cin>>n;for(int i=1;i<=n;i++) cin>>a[i];res=0;mergesort(1,n);
// cout<<res<<endl;if(res%2==1) minn=2;else minn=0;maxn=minn;maxn++;int base=4;while(base<=n){maxn+=base;base<<=1;}cout<<minn<<" "<<maxn<<endl;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--)solve();return 0;
}相关文章:
2023“钉耙编程”中国大学生算法设计超级联赛(7))
(杭电多校)2023“钉耙编程”中国大学生算法设计超级联赛(7)
1002 Random Nim Game 只有3种情况,要么必赢,要么必输,要么从宏观角度考虑,随机的话,赢的概率就是1/2(就像抛硬币一样,随着抛的次数越来越多,正反面的概率将越来越接近1) 当只要有一堆石头数量不是1,那么就是必赢或必输,赢的概率就是1/2 当每堆石头数量都为1时,当堆数为奇数…...
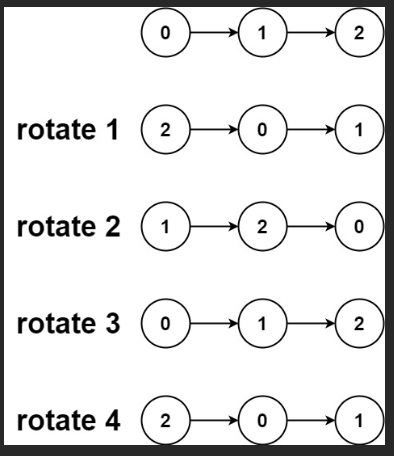
力扣:61. 旋转链表(Python3)
题目: 给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。 来源:力扣(LeetCode) 链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 示例&…...
)
笙默考试管理系统-MyExamTest----codemirror(1)
笙默考试管理系统-MyExamTest----codemirror(1) 目录 笙默考试管理系统-MyExamTest----codemirror(1) 一、 笙默考试管理系统-MyExamTest----codemirror 二、 笙默考试管理系统-MyExamTest----codemirror 三、 笙默考试管…...
)
【资料分享】全志科技T507工业核心板硬件说明书(二)
目 录 2引脚说明 2.1引脚排列 2.2引脚定义 2.3内部引脚使用说明 2.4引脚上下拉、串联说明 2.5功能引脚信号走线长度与阻抗说明 本文档为创龙科技SOM-TLT507工业...

PyTorch翻译官网教程-FAST TRANSFORMER INFERENCE WITH BETTER TRANSFORMER
官网链接 Fast Transformer Inference with Better Transformer — PyTorch Tutorials 2.0.1cu117 documentation 使用 BETTER TRANSFORMER 快速的推理TRANSFORMER 本教程介绍了作为PyTorch 1.12版本的一部分的Better Transformer (BT)。在本教程中,我们将展示如…...
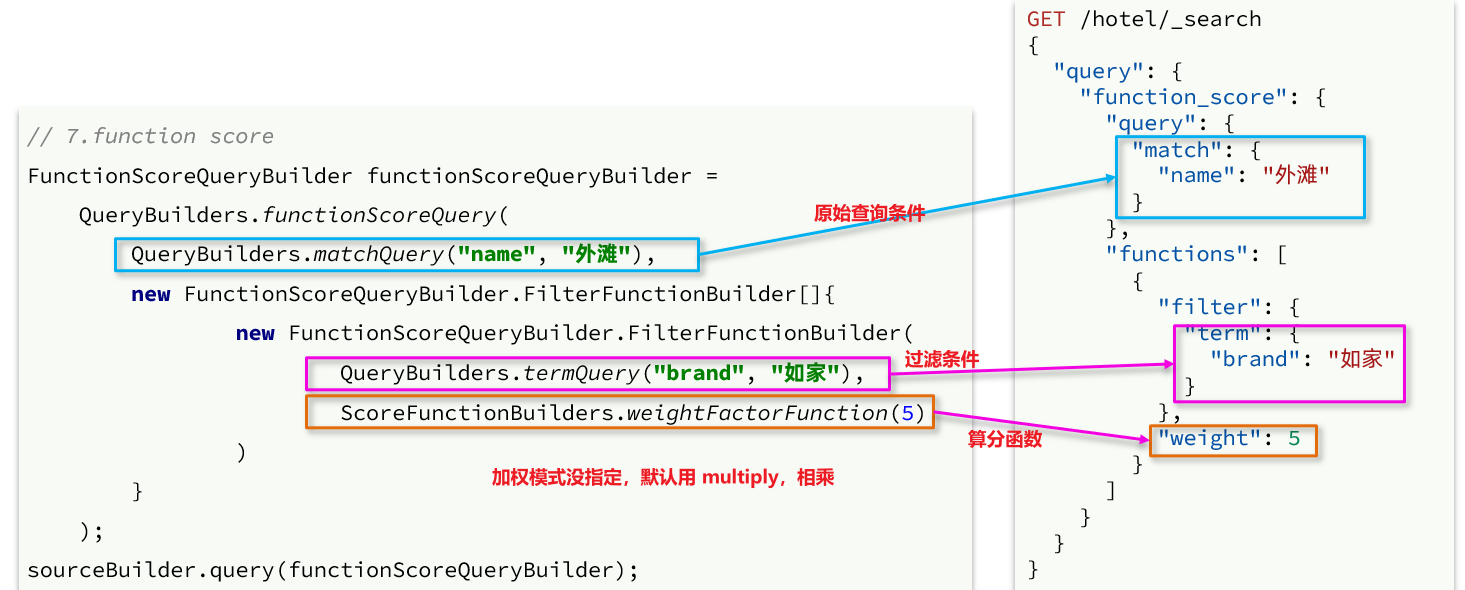
SpringCloud实用篇6——elasticsearch搜索功能
目录 1 DSL查询文档1.1 DSL查询分类1.2 全文检索查询1.2.1 使用场景1.2.2 基本语法1.2.3 示例1.2.4 总结 1.3 精准查询1.3.1 term查询1.3.2 range查询1.3.3 总结 1.4.地理坐标查询1.4.1 矩形范围查询1.4.2 附近查询 1.5 复合查询1.5.1 相关性算分1.5.2 算分函数查询1࿰…...

质量小议29 -- 循证
1. 循证 Evidence-Based遵循证据基于证据慎重、准确和明智地应用当前所能获得的最好研究依据利用证据追求实践科学化和专业化的价值观,重视证据指导实践的理念,运用证据解决实践中问题的思维,基于证据开展专业实践活动的指导原则,…...

微服务与Nacos概述-3
流量治理 在微服务架构中将业务拆分成一个个的服务,服务与服务之间可以相互调用,但是由于网络原因或者自身的原因,服务并不能保证服务的100%可用,如果单个服务出现问题,调用这个服务就会出现网络延迟,此时…...

Java 面试八股文
参考: 2023年 Java 面试八股文(20w字)_json解析失败_leader_song的博客-CSDN博客...

NPM与外部服务的集成(上)
目录 1、关于访问令牌 1.1 关于传统令牌 1.2 关于粒度访问令牌 2、创建和查看访问令牌 2.1 创建访问令牌 在网站上创建传统令牌 在网站上创建粒度访问令牌 使用CLI创建令牌 CIDR限制令牌错误 查看访问令牌 在网站上查看令牌 在CLI上查看令牌 令牌属性 1、关于访问令…...

React Router 6
1.概述 React Router 以三个不同的包发布到 npm 上,它们分别为: react-router: 路由的核心库,提供了很多的:组件、钩子。 react-router-dom: 包含react-router所有内容,并添加一些专门用于 DOM 的组件,例如…...
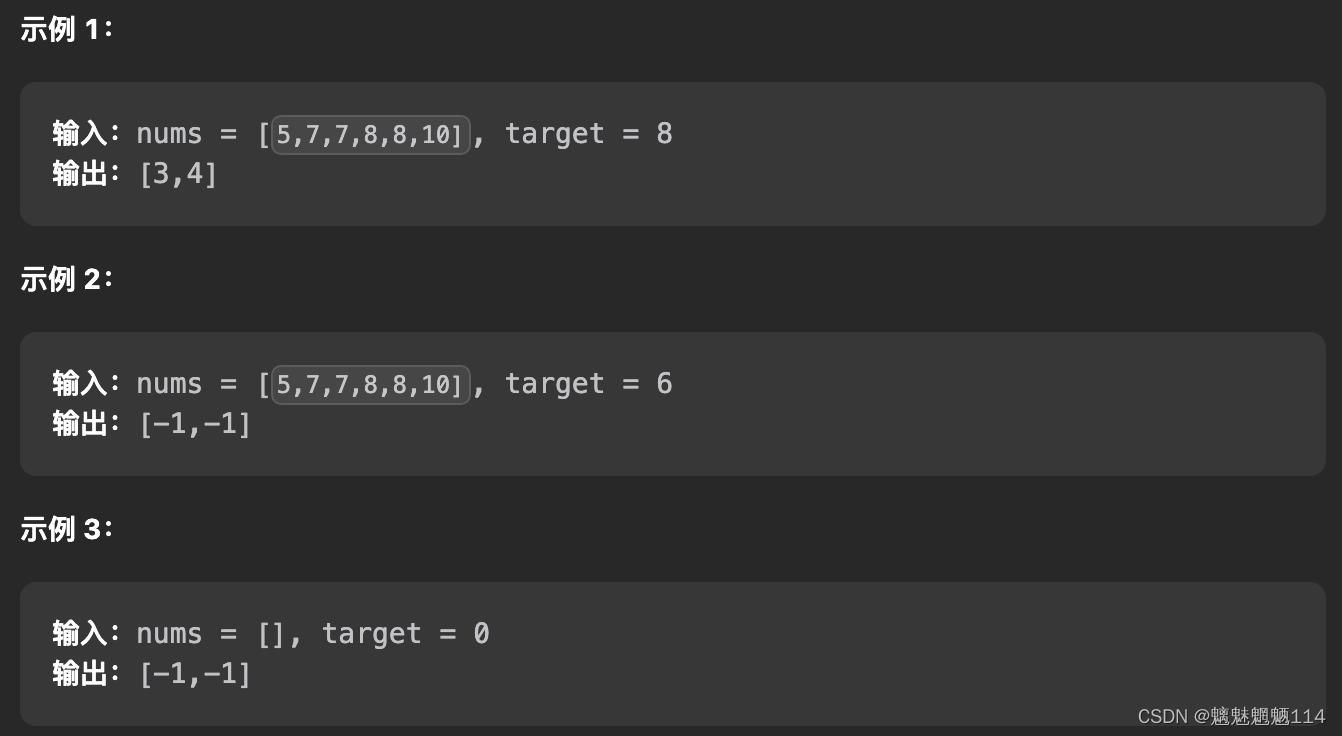
Leetcode34 在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。 如果数组中不存在目标值 target,返回 [-1, -1]。 你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。 代码: c…...
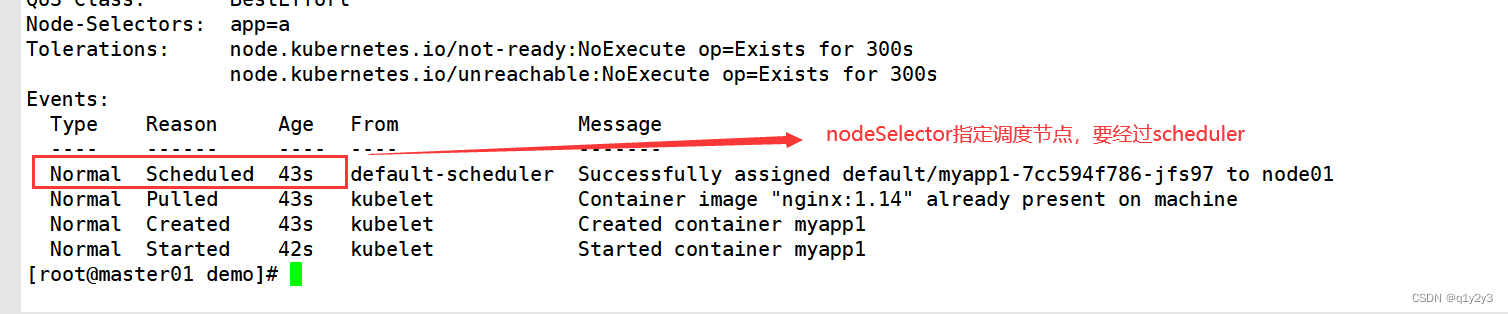
Kubernetes 调度约束(亲和性、污点、容忍)
目录 一、Pod启动典型创建过程 二、调度流程 三、指定调度节点 1.使用nodeName字段指定调度节点 2.使用nodeSelector指定调度节点 2.1给对应的node节点添加标签 2.2修改为nodeSelector调度方式 3.通过亲和性来指定调度节点 3.1节点亲和性 3.2Pod亲和性与反亲和性 3.2…...
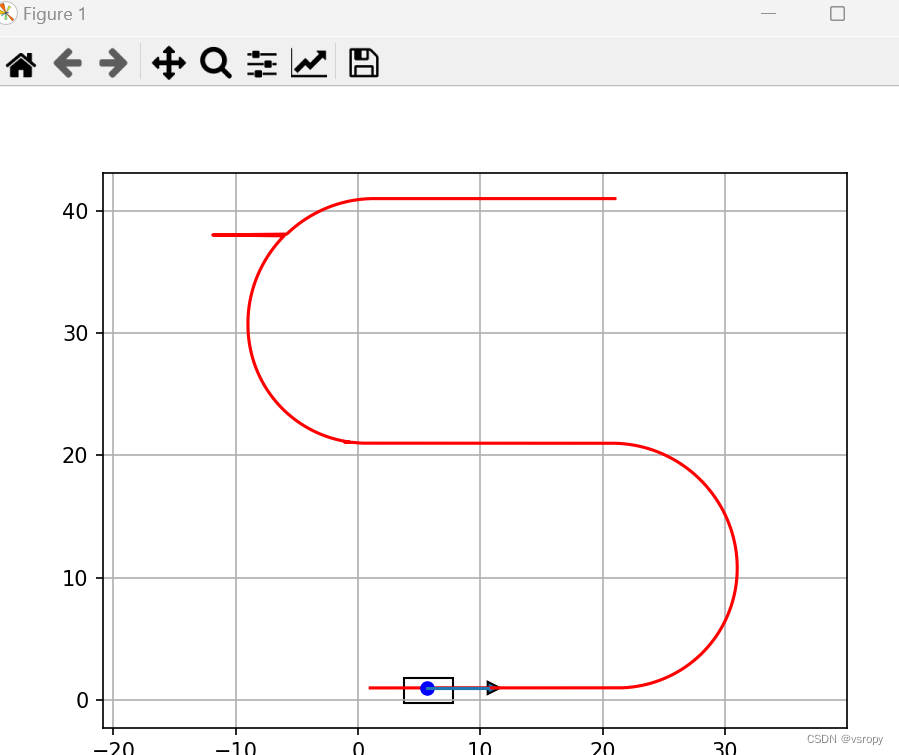
按轨迹运行
文章目录 import math import timeimport numpy as np import matplotlib.pyplot as pltdef plot_arrow(x, y, yaw, length=5, width=1):dx = length * math.cos(yaw)dy = length * math.sin(yaw)plt.arrow(x, y, dx, dy, head_length=width, head_width=width)plt.plot([x, x …...
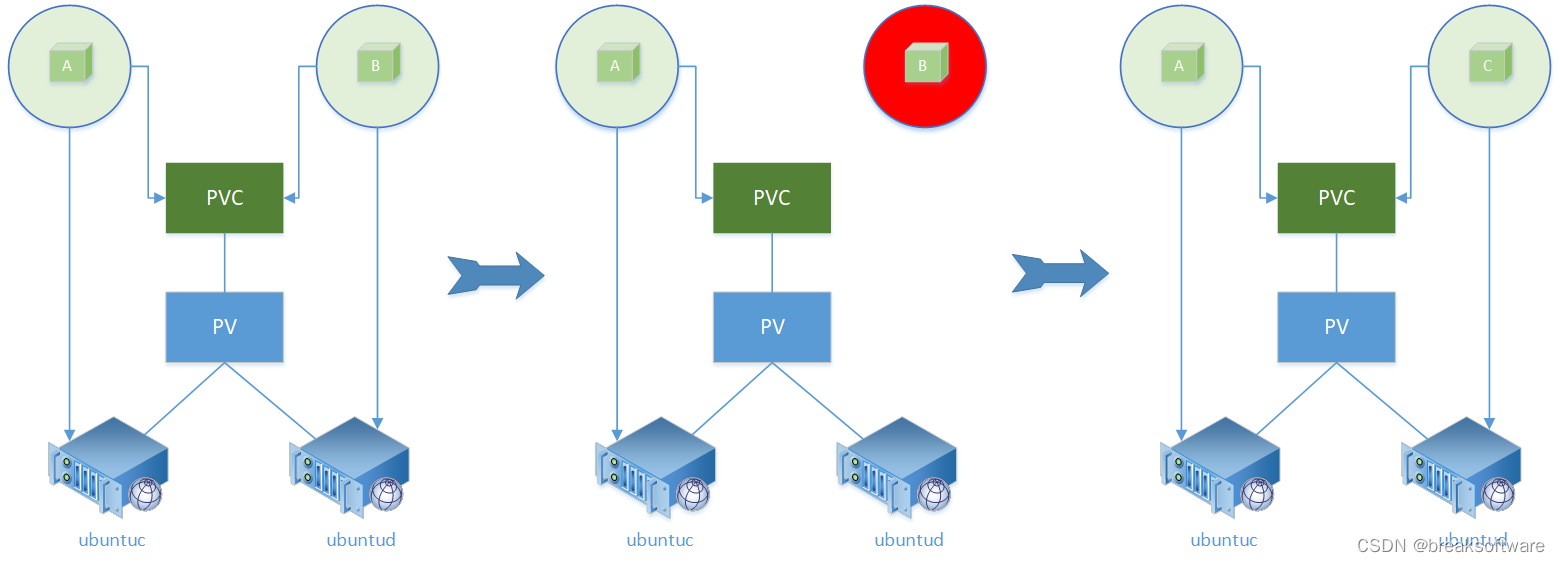
研发工程师玩转Kubernetes——通过PV的节点亲和性影响Pod部署
在《研发工程师玩转Kubernetes——PVC通过storageClassName进行延迟绑定》一文中,我们利用Node亲和性,让Pod部署在节点ubuntud上。因为Pod使用的PVC可以部署在节点ubuntuc或者ubuntud上,而系统为了让Pod可以部署成功,则让PVC与Pod…...
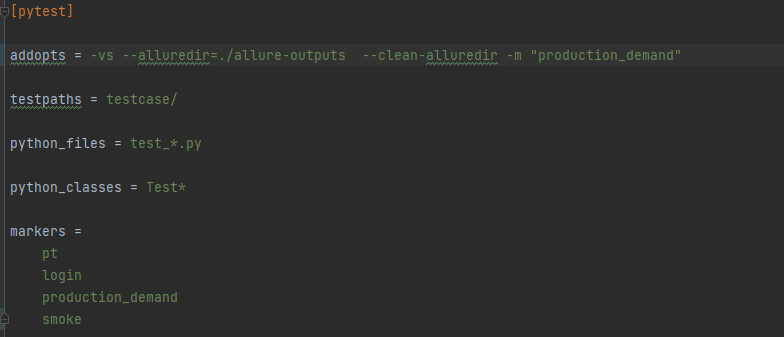
Pytest三种运行方式
Pytest 运行方式共有三种: 1、主函数模式 运行所有 pytest.main() 指定模块 pytest.main([-vs],,./testcase/test_day1.py) 只运行testcase 下的test_day1.py 文件 指定目录 pytest.main([-vs]),./testcase) 只运行testcase 目录下的文件 通过nodeid指定用例…...
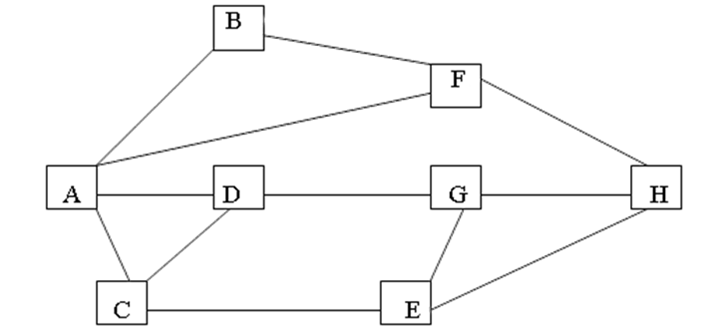
城市最短路
题目描述 下图表示的是从城市A到城市H的交通图。从图中可以看出,从城市A到城市H要经过若干个城市。现要找出一条经过城市最少的一条路线。 输入输出格式 输入格式: 无 输出格式: 倒序输出经过城市最少的一条路线 输入输出样例 输入样例…...
phpspreadsheet excel导入导出
单个sheet页Excel2003版最大行数是65536行。Excel2007开始的版本最大行数是1048576行。Excel2003的最大列数是256列,2007以上版本是16384列。 xlswriter xlswriter - PHP 高性能 Excel 扩展,功能类似phpspreadsheet。它能够处理非常大的文件࿰…...

自动驾驶传感器选型
360的场景,避免有盲区,长距离 Lidar(激光雷达) 典型特点一圈一圈的,轮廓和很高的位置精度 禾赛的机械雷达 速腾的固态雷达 固态雷达是车规级的,车规级的意思是可以装到量产车上 Radar(毫米…...
)
4.利用matlab符号矩阵的四则运算(matlab程序)
1.简述 符号对象的建立 sym函数 sym函数用于建立单个符号对象,其常用调用格式为: 符号对象名sym(A) 1 将由A来建立符号对象,其中,A可以是一个数值常量、数值矩阵或数值表达式(不加单引号),此时符号对象为一个符号常量;…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...
