数据结构笔记--常见二叉树分类及判断实现
目录
1--搜索二叉树
2--完全二叉树
3--平衡二叉树
4--满二叉树
1--搜索二叉树
搜索二叉树的性质:左子树的节点值都比根节点小,右子树的节点值都比根节点大;
如何判断一颗二叉树是搜索二叉树?
主要思路:
递归自底向上判断是否是一颗搜索二叉树,返回判断结果的同时,要返回对应的最小值和最大值;
#include <iostream>
#include <climits>struct TreeNode {int val;TreeNode *left, *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), right(nullptr) {}
};struct ReturnType{bool isBST = true;int max = 0;int min = 0;ReturnType(bool ib, int ma, int mi) : isBST(ib), max(ma), min(mi){}
};class Solution {
public:bool isBST(TreeNode *root){ReturnType res = dfs(root);return res.isBST;}ReturnType dfs(TreeNode *root){// 初始化最大值为整型最小值,最小值为整型最大值if(root == NULL) return ReturnType(true, INT_MIN, INT_MAX); ReturnType left = dfs(root->left);ReturnType right = dfs(root->right);bool isBST = true;if(!left.isBST || !right.isBST || left.max >= root->val || right.min <= root->val){isBST = false;}int min = std::min(std::min(root->val, left.min), std::min(root->val, right.min)); int max = std::max(std::max(root->val, left.max), std::max(root->val, right.max));return ReturnType(isBST, max, min);}
};int main(int argc, char *argv[]){TreeNode *Node1 = new TreeNode(4);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(6);TreeNode *Node4 = new TreeNode(1);TreeNode *Node5 = new TreeNode(3);TreeNode *Node6 = new TreeNode(5);TreeNode *Node7 = new TreeNode(7);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Node3->left = Node6;Node3->right = Node7;Solution S1;bool res = S1.isBST(Node1);if (res) std::cout << "true" << std::endl;else std::cout << "false" << std::endl;return 0;
}2--完全二叉树
如何判断一颗二叉树是完全二叉树?
主要思路:
层次遍历二叉树的节点,当遇到第一个节点(其左右儿子不双全)进行标记,往后遇到的所有节点应均为叶子节点,当遇到一个不是叶子节点时,返回 false 表明二叉树不是完全二叉树;
#include <iostream>
#include <queue>struct TreeNode {int val;TreeNode *left, *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), right(nullptr) {}
};class Solution {
public:bool isCBT(TreeNode *root){if(root == NULL) return true;std::queue<TreeNode*> q;q.push(root);bool flag = false; while(!q.empty()){ // 层次遍历TreeNode *cur = q.front();q.pop();if(cur->left != NULL) q.push(cur->left);if(cur->right != NULL) q.push(cur->right);if( // 标记节点后,还遇到了不是叶子节点的节点,返回false(flag == true && (cur->left != NULL || cur->right != NULL)) || // 左儿子为空,右儿子不为空,返回false(cur->left == NULL && cur->right != NULL)) return false;// 遇到第一个左右儿子不双全的节点进行标记if(cur->left == NULL || cur->right == NULL) flag = true;}return true;}
};int main(int argc, char *argv[]){TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(3);TreeNode *Node4 = new TreeNode(4);TreeNode *Node5 = new TreeNode(5);TreeNode *Node6 = new TreeNode(6);TreeNode *Node7 = new TreeNode(7);TreeNode *Node8 = new TreeNode(8);TreeNode *Node9 = new TreeNode(9);TreeNode *Node10 = new TreeNode(10);TreeNode *Node11 = new TreeNode(11);TreeNode *Node12 = new TreeNode(12);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Node3->left = Node6;Node3->right = Node7;Node4->left = Node8;Node4->right = Node9;Node5->left = Node10;Node5->right = Node11;Node6->left = Node12;Solution S1;bool res = S1.isCBT(Node1);if (res) std::cout << "true" << std::endl;else std::cout << "false" << std::endl;return 0;
}3--平衡二叉树
平衡二叉树要求:左子树和右子树的高度差 <= 1;
如何判断一颗二叉树是平衡二叉树?
主要思路:
递归自底向上判断是否是一颗平衡二叉树,返回判断结果的同时,要返回对应的深度;
#include <iostream>
#include <queue>struct TreeNode {int val;TreeNode *left, *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), right(nullptr) {}
};struct ReturnType{bool isbalanced = true;int height = 0;ReturnType(bool ib, int h) : isbalanced(ib), height(h) {}
};class Solution {
public:bool isBalanced(TreeNode *root){ReturnType res = dfs(root);return res.isbalanced;}ReturnType dfs(TreeNode *root){if(root == NULL) return ReturnType(true, 0);ReturnType left = dfs(root->left);ReturnType right = dfs(root->right);int cur_height = std::max(left.height, right.height) + 1; bool cur_balanced = left.isbalanced && right.isbalanced && std::abs(left.height - right.height) <= 1;return ReturnType(cur_balanced, cur_height);}private:int height = 0;
};int main(int argc, char *argv[]){TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(3);TreeNode *Node4 = new TreeNode(4);TreeNode *Node5 = new TreeNode(5);TreeNode *Node6 = new TreeNode(6);TreeNode *Node7 = new TreeNode(7);TreeNode *Node8 = new TreeNode(8);TreeNode *Node9 = new TreeNode(9);TreeNode *Node10 = new TreeNode(10);TreeNode *Node11 = new TreeNode(11);TreeNode *Node12 = new TreeNode(12);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Node3->left = Node6;Node3->right = Node7;Node4->left = Node8;Node4->right = Node9;Node5->left = Node10;Node5->right = Node11;Node6->left = Node12;Solution S1;bool res = S1.isBalanced(Node1);if (res) std::cout << "true" << std::endl;else std::cout << "false" << std::endl;return 0;
}4--满二叉树
满二叉树的判断:节点数 = 2^深度 - 1;
如何判断一颗二叉树是平衡二叉树?
主要思路:
递归自底向上判断是否是一颗满二叉树,返回判断结果的同时,要返回对应的深度和节点数;
#include <iostream>
#include <queue>struct TreeNode {int val;TreeNode *left, *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), right(nullptr) {}
};struct ReturnType{bool isFCT = true;int height = 0;int nodes = 0;ReturnType(bool ib, int h, int n) : isFCT(ib), height(h), nodes(n){}
};class Solution {
public:bool isFCT(TreeNode *root){ReturnType res = dfs(root);return res.isFCT;}ReturnType dfs(TreeNode *root){if(root == NULL) return ReturnType(true, 0, 0);ReturnType left = dfs(root->left);ReturnType right = dfs(root->right);bool isFCT = true;int cur_nodes = left.nodes + right.nodes + 1;int cur_height = std::max(left.height, right.height) + 1;if(!left.isFCT || !right.isFCT || (1<<cur_height) - 1 != cur_nodes){isFCT = false;}return ReturnType(isFCT, cur_height, cur_nodes);}
};int main(int argc, char *argv[]){TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(3);TreeNode *Node4 = new TreeNode(4);TreeNode *Node5 = new TreeNode(5);TreeNode *Node6 = new TreeNode(6);TreeNode *Node7 = new TreeNode(7);TreeNode *Node8 = new TreeNode(8);TreeNode *Node9 = new TreeNode(9);TreeNode *Node10 = new TreeNode(10);TreeNode *Node11 = new TreeNode(11);TreeNode *Node12 = new TreeNode(12);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Node3->left = Node6;Node3->right = Node7;Node4->left = Node8;Node4->right = Node9;Node5->left = Node10;Node5->right = Node11;Node6->left = Node12;Solution S1;bool res = S1.isFCT(Node1);if (res) std::cout << "true" << std::endl;else std::cout << "false" << std::endl;return 0;
}相关文章:

数据结构笔记--常见二叉树分类及判断实现
目录 1--搜索二叉树 2--完全二叉树 3--平衡二叉树 4--满二叉树 1--搜索二叉树 搜索二叉树的性质:左子树的节点值都比根节点小,右子树的节点值都比根节点大; 如何判断一颗二叉树是搜索二叉树? 主要思路: 递归自底向…...
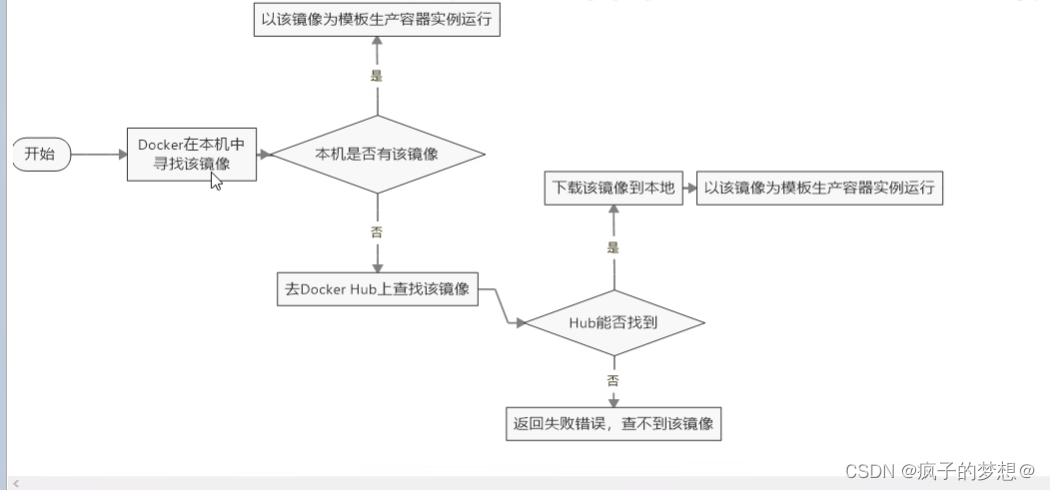
docker小白第二天
centos上安装docker docker官网,docker官网,找到下图中的doc文档。 进入如下页面 选中manuals,安装docker引擎。 最终centos下的docker安装文档链接:安装文档链接. 具体安装步骤: 1、打开Centos,输入命…...
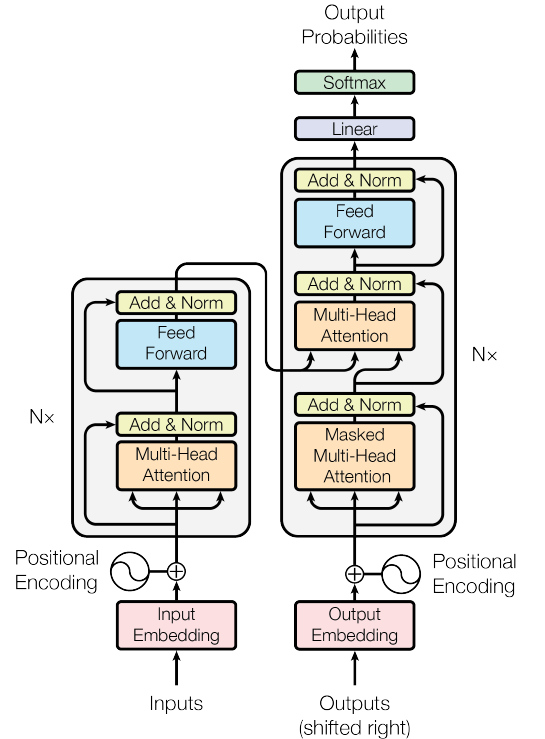
【变形金刚03】使用 Pytorch 开始构建transformer
一、说明 在本教程中,我们将使用 PyTorch 从头开始构建一个基本的转换器模型。Vaswani等人在论文“注意力是你所需要的一切”中引入的Transformer模型是一种深度学习架构,专为序列到序列任务而设计,例如机器翻译和文本摘要。它基于自我注意机…...
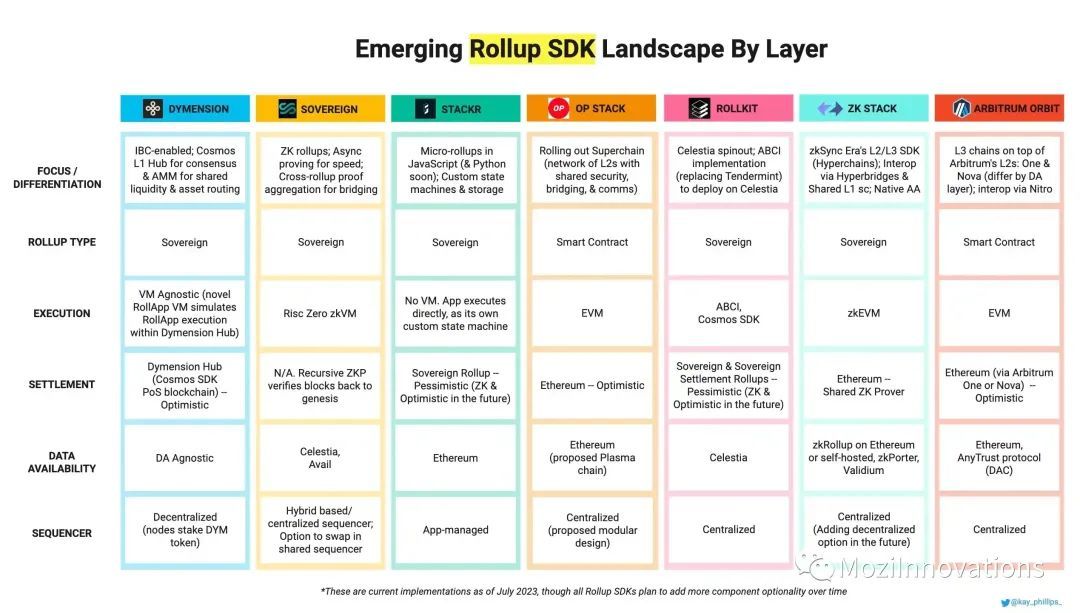
「Web3大厂」价值70亿美元的核心竞争力
经过近 5 年的研发和酝酿,Linea 团队在 7 月的巴黎 ETHCC 大会期间宣布了主网 Alpha 的上线,引起了社区的广泛关注。截止 8 月 4 日,据 Dune 数据信息显示,其主网在一周内就涌入了 100 多个生态项目,跨入了超 2 万枚 E…...

前端发送请求和后端springboot接受参数
0.xhr、 ajax、axios、promise和async/await 和http基本方法 xhr、 ajax、axios、promise和async/await都是异步编程和网络请求相关的概念和技术! xhr:XMLHttpRequest是浏览器提供的js对象(API),用于请求服务器资源。…...

程序一直在阿里云服务器运行
保持阿里云服务器开机程序保持运行. 1.下载Screen CentOS 系列系统: yum install screen Ubuntu 系列系统: sudo apt-get install screen 2、运行screen,创建一个screen screen -S name:name是标记进程, 给进程备注…...

Linux 文件与目录管理
nvLinux 文件与目录管理 我们知道 Linux 的目录结构为树状结构,最顶级的目录为根目录 /。 其他目录通过挂载可以将它们添加到树中,通过解除挂载可以移除它们。 在开始本教程前我们需要先知道什么是绝对路径与相对路径。 绝对路径: 路径的写…...

【CSS】CSS 布局——弹性盒子
Flexbox 是一种强大的布局系统,旨在更轻松地使用 CSS 创建复杂的布局。 它特别适用于构建响应式设计和在容器内分配空间,即使项目的大小是未知的或动态的。Flexbox 通常用于将元素排列成一行或一列,并提供一组属性来控制 flex 容器内的项目行…...
)
“华为杯”研究生数学建模竞赛2018年-【华为杯】B题:光传送网建模与价值评估(附优秀论文及matlab代码实现)
目录 摘要: 1.问题重述 1.1 问题背景 1.2 问题提出 2.问题假设 3.符号说明...
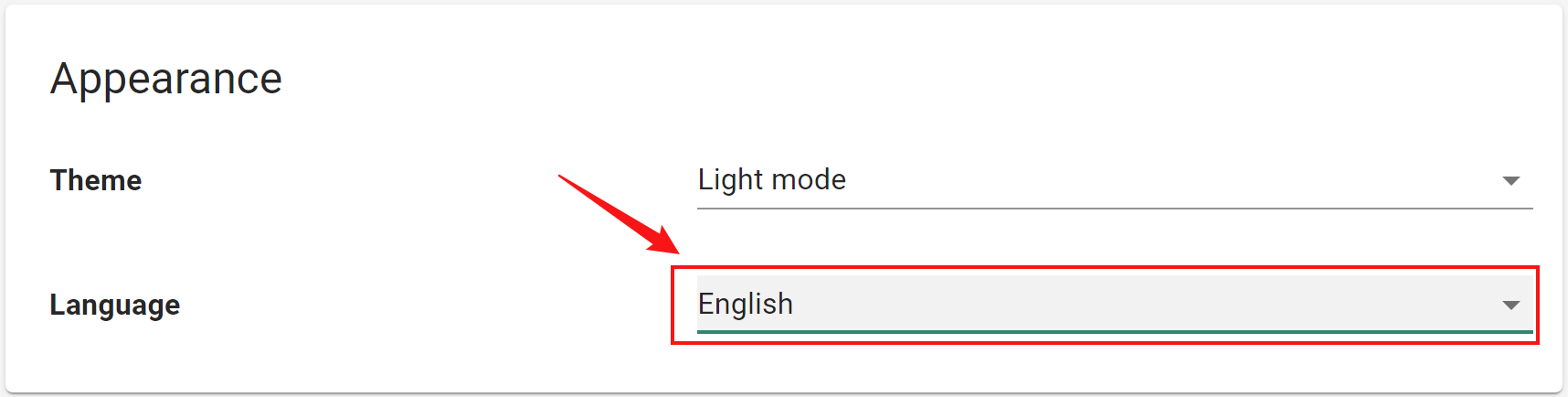
群晖 nas 自建 ntfy 通知服务(梦寐以求)
目录 一、什么是 ntfy ? 二、在群晖nas上部署ntfy 1. 在Docker中安装ntfy 2. 设置ntfy工作文件夹 3. 启动部署在 docker 中的 ntfy(binwiederhier/ntfy) 三、启动配置好后,如何使用ntfy 1. 添加订阅主题( Subscribe to topic…...
)
Java基础练习九(方法)
求和 设计一个方法,用于计算整数的和 public class Work1101 {public static void main(String[] args) {// 设计一个方法,用于计算整数的和System.out.println(sum(7, 6));}public static int sum(int a, int b) {return a b;} }阶乘 编写一个方法&…...
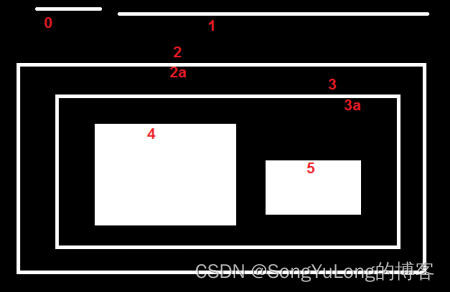
Python-OpenCV中的图像处理-图像轮廓
Python-OpenCV中的图像处理-图像轮廓 轮廓什么是轮廓查找轮廓绘制轮廓轮廓特征图像的矩轮廓面积轮廓周长(弧长)轮廓近似凸包凸性检测边界矩形直边界矩形旋转边界矩形(最小面积矩形)最小外接圆最小外接三角椭圆拟合直线拟合 轮廓的…...

@Cacheable缓存相关使用总结
本篇文章主要讲解Spring当中Cacheable缓存相关使用 在实际项目开发中,有些数据是变更频率比较低,但是查询频率比较高的,此时为了提升系统性能,可以使用缓存的机制实现,避免每次从数据库获取 第一步:使用E…...

c++ static
static 成员 声明为static的类成员称为类的静态成员,用static修饰的成员变量,称之为静态成员变量;用 static修饰的成员函数,称之为静态成员函数。静态成员变量一定要在类外进行初始化。 看看下面代码体会一下: //其他类 class …...
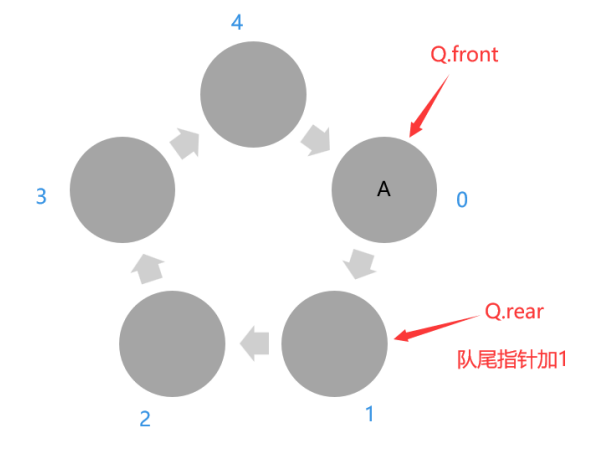
【数据结构】——栈、队列的相关习题
目录 题型一(栈与队列的基本概念)题型二(栈与队列的综合)题型三(循环队列的判空与判满)题型四(循环链表表示队列)题型五(循环队列的存储)题型六(循…...

C++初阶之一篇文章教会你list(模拟实现)
list(模拟实现) list模拟实现list_node节点结构定义std::__reverse_iterator逆向迭代器实现list迭代器 __list_iterator定义list类成员定义list成员函数定义1.begin()、end()、rbegin()和rend()2.empty_init()3.构造函数定义4.swap5.析构函数定义6.clear…...
设备工单管理系统如何实现工单流程自动化?
设备工单管理系统属于工单系统的一种,基于其丰富的功能,它可以同时处理不同的多组流程,旨在有效处理发起人提交的事情,指派相应人员完成服务请求和记录全流程。该系统主要面向后勤管理、设备维护、物业管理、酒店民宿等服务行业设…...

ubuntu20.04.6anzhuang mtt s80
需要打开主板的Resize BAR和Above 4G功能,否则GPU显存不能被正确识别; 2. 在某些不支持PCIe Gen5的主板上,需要把PCIe速率由auto设置为PCIe Gen4速率; sudo apt install lightdm unity-greetersheding lightdm : lightdm sudo apt install /…...

【LeetCode-中等】剑指 Offer 36. 二叉搜索树与双向链表
题目链接 剑指 Offer 36. 二叉搜索树与双向链表 标签 后序遍历、二叉搜索树 步骤 二叉搜索树中的任一节点的直接前驱为其左子树的最右侧节点,直接后继为其右子树的最左侧节点。因此,可以通过这个关系来操作原来的二叉树。为了不影响深度较大的节点的…...
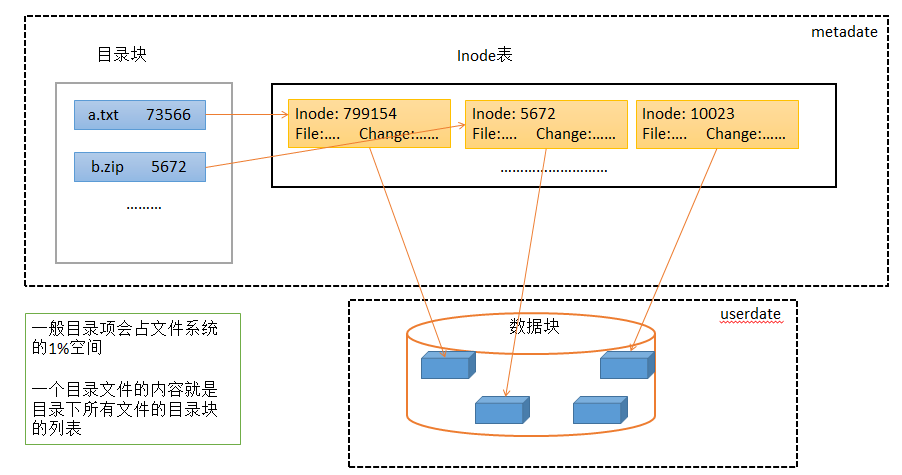
Linux —— 文件系统
目录 一,背景 二,文件系统 一,磁盘简介 磁盘分为SSD、机械磁盘;机械磁盘,即磁盘高速转动,磁头移动到读写扇区所在磁道,让磁头在目标扇区上划过,即可完成对扇区的读写操作ÿ…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
