期权定价模型系列【4】—期权组合的Delta-Gamma-Vega中性
期权组合的Delta-Gamma-Vega中性
期权组合构建时往往会进行delta中性对冲,在进行中性对冲后,期权组合的delta敞口为0,此时期权组合仍然存在gamma与vega敞口。因此研究期权组合的delta-gamma-vega敞口中性是有必要的。
本文旨在对delta-gamma-vega中性对冲的理论分析,具体的代码可以参考【期权量化】专栏,专栏地址如下:
http://t.csdn.cn/lHoxt![]() http://t.csdn.cn/lHoxt
http://t.csdn.cn/lHoxt
1.前言
回顾一下:Delta表示期权价格对标的资产价格变化的敏感度,即标的资产价格变动一个单位时,期权价格的变化量。Gamma表示Delta随标的资产价格变化而变化的敏感度。即标的资产价格变动一个单位时,Delta的变化量。Vega表示期权价格对标的资产波动率的敏感度,即期权价格变化与隐含波动率变化的比值。
期权作为一个复杂的非线性金融衍生品,影响其价值的因素有很多。在这诸多因素中,对期权价值影响最为直接的是期权标的资产的价值。为了量化这一影响,人们在期权定价公式中定义了delta 的概念,并从数学的角度上证明出,如果一个期权投资组合保持动态的保持delta中性,就能消除标的资产价格变动对该组合产生的损益影响。
在持有一个进行delta动态对冲并保持delta中性的投资组合中,标的资产价格的变动不再是影响投资组合损益的主要因素了。然而,由于期权产品的复杂性,仍然有许多其他的因素能够左右投资组合的损益情况,这其中,起主导作用的是gamma风险,vega风险,甚至是利率风险以及股息风险。
与标的资产delta为1不同,标的资产的gamma与vega均为0,因此通过标的资产的数量变动并不可以改变期权组合的gamma与vega头寸。与gamma头寸类似,期权的vega头寸的调整需要引入与标的资产有关的衍生品才可以达到目的。也就是说,当一个期权组合通过调整标的资产价格达到delta中性时,该组合往往还存在gamma与vega方向的暴露,因此还需要引入衍生品来调整gamma与vega头寸。
2.期权组合的delta
当持有期权头寸时,为了保证投资组合的delta中性,会卖出与期权头寸delta等量的期货合约来对冲。一个平值的期权的delta值通常在0.5左右。若期权处于实值阶段,则期权的delta将会趋近于1,这代表着深度实值的期权近似的等价于一手具有同等合约大小的期货合约。类似的,如期权处于虚值阶段,则期权的delta将会趋近于0,这代表着深度虚职的期权合约不具备任何价值。
3.期权组合的gamma损益
当我们持有一个期权头寸时,在期权到期之前,我们可以用期货来持续的动态对冲掉期权头寸的delta以保持整个投资组合的delta中性,此delta动态对冲过程中,会不断买入或者卖出期货合约,这些用以对冲而买进或者卖出的期货合约便会在总头寸中不断的累积损益。通常来说,在买入期权的投资组合中,delta中性对冲后整体投资组合的损益往往是负的,而在卖出期权的投资组合中,delta中性对中后整体投资组合的损益往往是正的。这一损益就是我们常常说的gamma损益。
4.期权组合的vega
从Black Scholes公式中我们知道,影响期权价值的还有波动率水平这一因素。在期权生效的期间内,标的指数的波动率水平往往是不断变化的,波动率的变化也会给期权带来vega损益。一般的,当波动率水平升高时,由于标的指数波动的幅度更大了,则期权更有可能在到期时变为实值,期权的价值也会随之升高。相反的,当波动率水平降低时,期权的价值会随之降低。当然,如果投资者一直按照购买期权的初始隐含波动率为标准来计算delta并进行delta中性对冲,并持续这一过程直到期权到期,那么从期权购买直至到期这一段时间内,波动率带来的vega损益将会是0。
5.例子
考虑一个delta中性组合,其gamma为-5000,vega为-8000。此时购买4000份期权1使得组合变为vega中性(期权1的delta为0.6,gamma为0.5,vega为2)这样使得组合的delta变为2400,为了delta中性,必须卖出2400份标的资产,组合的gamma也变为-3000。为了保证gamma和vega中性,需要将期权1与期权2(delta为0.5,gamma为0.8,vega为1.2)加入到组合中,那么有:
-5000+0.5w1+0.8w2=0
-8000+2w1+1.2w2=0
求解得到w1=400,w2=6000,也就是说同时加入400份期权1与6000份期权2可以使得组合变为gamma与vega中性。此时组合delta变为3240,还需要卖出3240份标的资产才可使得组合变为delta中性。通过上述操作,便可使得期权组合变为一个delta-gamma-vega中性的组合。
6.代码部分
具体代码可以参考【期权量化】专栏的同名文章
相关文章:
期权定价模型系列【4】—期权组合的Delta-Gamma-Vega中性
期权组合的Delta-Gamma-Vega中性 期权组合构建时往往会进行delta中性对冲,在进行中性对冲后,期权组合的delta敞口为0,此时期权组合仍然存在gamma与vega敞口。因此研究期权组合的delta-gamma-vega敞口中性是有必要的。 本文旨在对delta-gamma-…...

k8sday02
第四章 实战入门 本章节将介绍如何在kubernetes集群中部署一个nginx服务,并且能够对其进行访问。 Namespace Namespace是kubernetes系统中的一种非常重要资源,它的主要作用是用来实现多套环境的资源隔离或者多租户的资源隔离。 默认情况下&…...
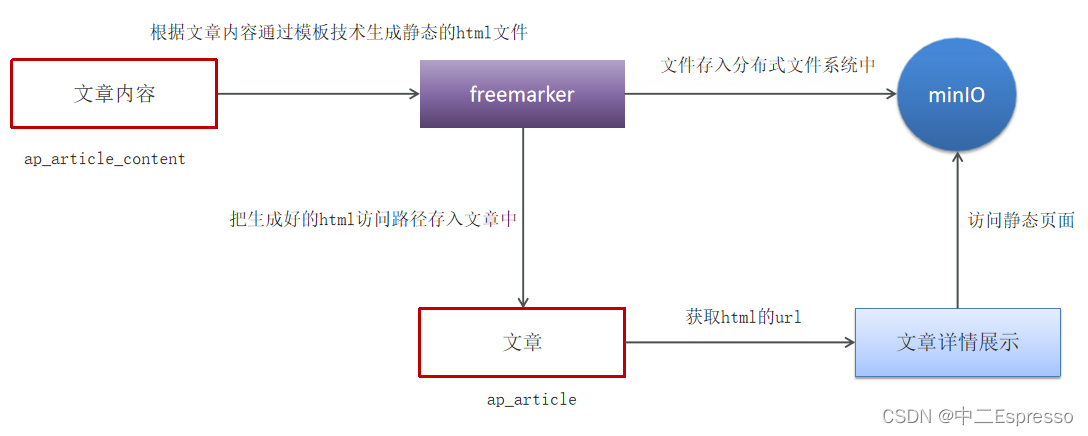
黑马头条项目学习--Day2: app端文章查看,静态化freemarker,分布式文件系统minIO
app端文章 Day02: app端文章查看,静态化freemarker,分布式文件系统minIOa. app端文章列表查询1) 需求分析2) 实现思路 b. app端文章详细1) 需求分析2) Freemarker概述a) 基础语法种类b) 集合指令(List和Map)c) if指令d) 运算符e) 空值处理f) …...
特语云用Linux和MCSM面板搭建 我的世界基岩版插件服 教程
Linux系统 用MCSM和DockerWine 搭建 我的世界 LiteLoaderBDS 服务器 Minecraft Bedrock Edition 也就是我的世界基岩版,这是 Minecraft 的另一个版本。Minecraft 基岩版可以运行在 Win10、Android、iOS、XBox、switch。基岩版不能使用 Java 版的服务器,…...

2023.8
编译 make install 去掉 folly armv8-acrc arrow NEON 相关链接 https://blog.csdn.net/u011889952/article/details/118762819 这里面的方案二,我之前也是用的这个 https://blog.csdn.net/zzhongcy/article/details/105512565 参考的此博客 火焰图 https://b…...
CSV文件编辑器——Modern CSV for mac
Modern CSV for Mac是一款功能强大、操作简单的CSV文件编辑器,适用于Mac用户快速、高效地处理和管理CSV文件。Modern CSV具有直观的用户界面,可以轻松导入、编辑和导出CSV文件。它支持各种功能,包括排序、过滤、查找和替换,使您能…...
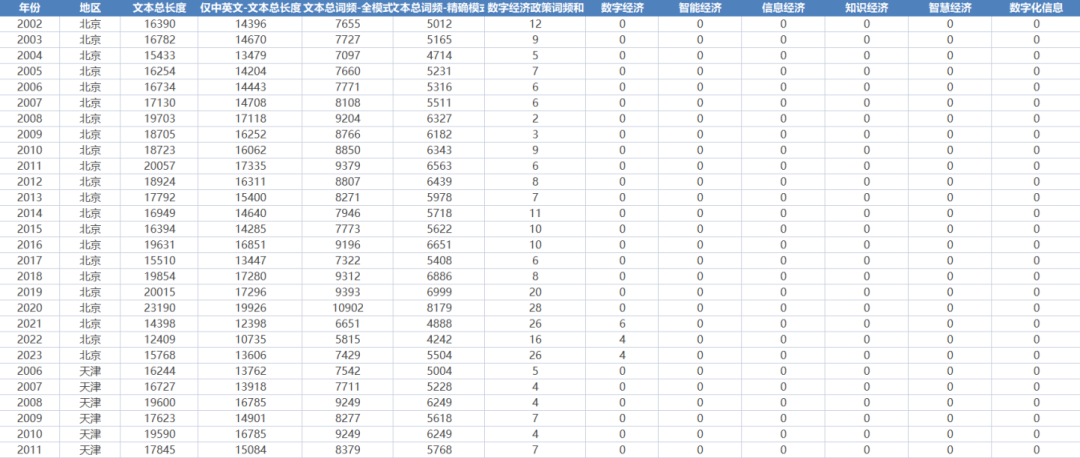
全国各地区数字经济工具变量-文本词频统计(2002-2023年)
数据简介:本数据使用全国各省工作报告,对其中数字经济相关的词汇进行词频统计,从而构建数字经济相关的工具变量。凭借数字经济政策供给与数字经济发展水平的相关系数的显著性作为二者匹配程度的划分依据,一定程度上规避了数字经济…...

MacOS安装RabbitMQ
官网地址: RabbitMQ: easy to use, flexible messaging and streaming — RabbitMQ 一、brew安装 brew update #更新一下homebrew brew install rabbitmq #安装rabbitMQ 安装结果: > Caveats > rabbitmq Management Plugin enabled by defa…...
关于selenium 元素定位的浅度解析
一、By类单一属性定位 元素名称 描述 Webdriver API id id属性 driver.find_element(By.ID, "id属性值") name name属性 driver.find_element(By.NAME, "name属性值") class_name class属性 driver.find_element(By.CLASS_NAME, "class_na…...

狐猬编程:货运
玩具厂生产了一批玩具需要运往美国销售。该批玩具根据大小,已经将其打包装在不同的包装盒里用以运输。该批玩具包装盒共有六个型号,分别1*1*h、2*2*h、3*3*h、4*4*h、5*5*h、6*6*h的包装盒。由于疫情的影响,运输价格十分昂贵,海运…...
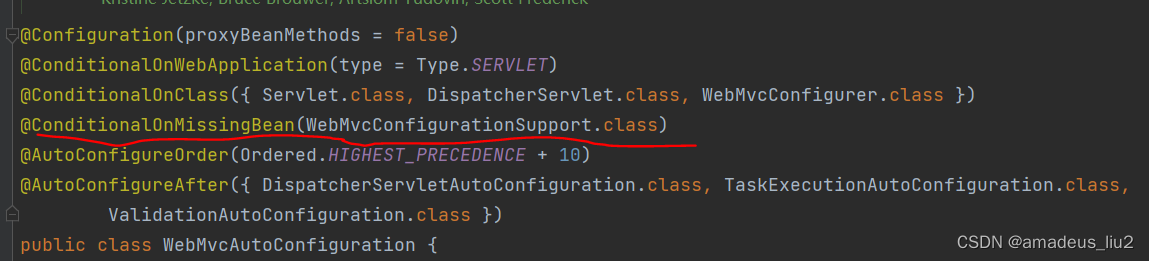
SpringBoot复习:(34)@EnableWebMvc注解为什么让@WebMvcAutoconfiguration失效?
它导入了DelegatingWebMvcConfiguration 它会把容器中的类型为WebMvcConfigurer的bean注入到类型为WebMvcConfigurerComposite的成员变量configurers中。 可以看到它继承了WebMvcConfigurerSupport类 而WebMvcConfigureAutoConfiguration类定义如下 可以看到一个Conditional…...

批量将CSV文件转换为TXT文件
要批量将CSV文件转换为TXT文件,可以按照以下步骤进行操作: 1. 导入所需的Python库:首先,您需要导入csv库来读取CSV文件。 import csv 2. 定义文件路径和输出文件夹: input_folder "your_input_folder_path&q…...

vite跨域配置踩坑,postman链接后端接口正常,但是前端就是不能正常访问
问题一:怎么都链接不了后端地址 根据以下配置,发现怎么都链接不了后端地址,proxy对了呀。 仔细看,才发现host有问题 // 本地运行配置,及反向代理配置server: {host: 0,0,0,0,port: 80,// cors: true, // 默认启用并允…...
模式)
Java设计模式-抽象工厂(Abstract Factory)模式
说明 抽象工厂(Abstract Factory)模式是一种工厂模式。用一个接口类中的不同方法创建不同的产品。 为了便于理解,先打个比方: 将老虎、狮子、猴子比作三个抽象产品的接口类,也就是有3个产品等级。 老虎又分动物园的…...

Hive加密,PostgreSQL解密还原
当前公司数据平台使用的处理架构,由Hive进行大数据处理,然后将应用数据同步到PostgreSQL中做各类外围应用。由于部分数据涉及敏感信息,必须在Hive进行加密,然后在PG使用时再进行单个数据解密,并监控应用的数据调用事情…...
2023年测试岗,接口测试面试题汇总+答案,拿捏面试官...
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、你们公司的接口…...

C# --- Case Study
C# --- Case Study C# — Mongo数据库事务的应用 C# — 如何解析Json文件并注入MongoDB C# — MongoDB如何安全的替换Collection...
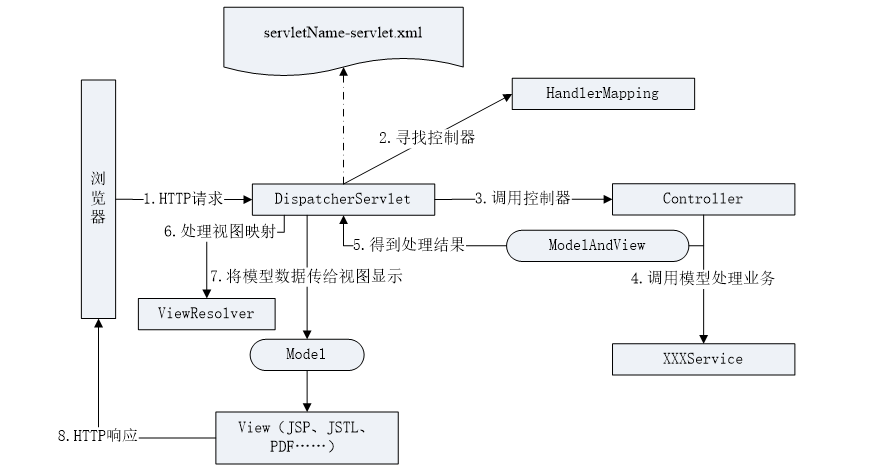
3.1 Spring MVC概述
1. MVC概念 MVC是一种编程思想,它将应用分为模型(Model)、视图(View)、控制器(Controller)三个层次,这三部分以最低的耦合进行协同工作,从而提高应用的可扩展性及可维护…...

Towards Open World Object Detection【论文解析】
Towards Open World Object Detection 摘要1 介绍2 相关研究3 开放世界目标检测4 ORE:开放世界目标检测器4.1 对比聚类4.2 RPN自动标注未知类别4.3 基于能量的未知标识4.4 减少遗忘 5 实验5.1开放世界评估协议5.2 实现细节5.3 开放世界目标检测结果5.4 增量目标检测结果 6 讨论…...
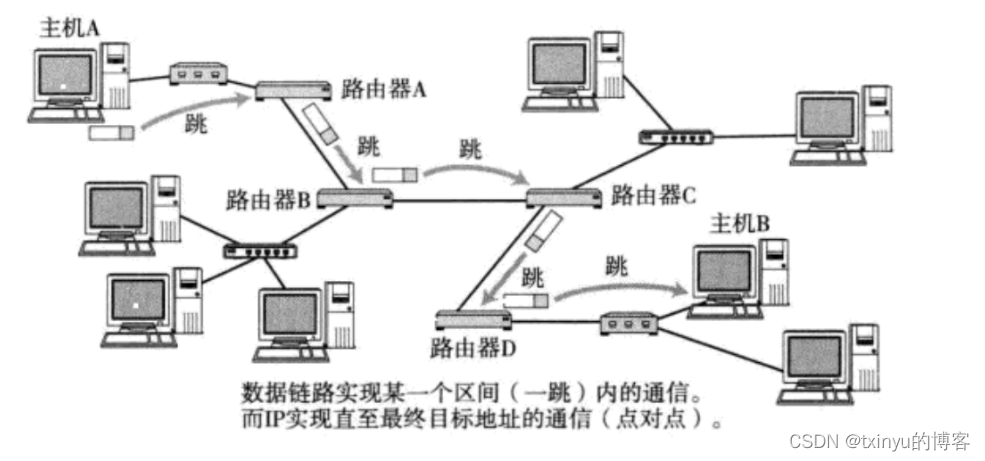
IP协议
目录 网络层 理解路由选择 IP协议 IP首部 IP分片原理 IP校验和原理 网段划分 IP地址数量限制 私有和公网IP地址 路由 什么是IP地址,IP地址有什么特征?IP地址和MAC地址有什么区别和联系? IP报文由IP头部和IP数据两个部分组成&#…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
