数据结构---跳表
目录标题
- 为什么会有跳表
- 跳表的原理
- 跳表的模拟实现
- 准备工作
- find函数
- insert函数
- erase函数
- 测试
- 效率比较
为什么会有跳表
在前面的学习过程中我们学习过链表这个容器,这个容器在头部和尾部插入数据的时间复杂度为O(1),但是该容器存在一个缺陷就是不管数据是否有序查找数据是否存在的时间复杂度都是O(N),我们只能通过暴力循环的方式查找数据是否存在,尽管数据是有序的我们也不能通过二分查找的形式去查找一个数据,那么为了解决这个问题就有人提出来了跳表这个容器。
跳表的原理
之前学习的链表结构如下:

那么跳表的思路就是:每相邻两个节点升高一层,增加一个指针,让指针指向下下个节点

这样所有新增加的指针连成了一个新的链表,但它包含的节点个数只有原来的一半。由于新增加的指针,我们不再需要与链表中每个节点逐个进行比较了,需要比较的节点数大概只有原来的一半。比如说要查找元素19,首先就比较头结点最上面指针指向的节点(节点中的元素为6)是否大于19,如果大于就跳转到该节点,那么很明显这里是大于的所以跳转到节点6上,然后接着比较元素6最上面的指针指向的节点(节点9)是否大于19,很明显是晓得所以跳转到元素9上,然后接着就来到节点17,因为节点17最上面的节点指向的元素是21比19大,那么这时就不能往该指针指向的节点进行跳转,我们得比较该指针下面的指针(17号节点中下方指针)指向的节点,该节点指向的值刚好为19所以就找到了指定元素,那么这就是跳表查找元素的原理

可是上面的查找过程并没有提高很大的效率最好的情况也是O(N/2),所以为了进一步的提高效率我们在第二层新产生的链表上,继续为每相邻的两个节点升高一层增加一个指针,从而产生第三层链表:

那么这时查找元素19就会变的更快,经过一次比较就来到了节点9,然后就跳转到节点17,最后就来到了节点19:

可以看到再添加一层节点就会使得节点查找的效率变的更高,那么同样的道理只要链表的数据个数够长我们还可以添加多层这样以此类推直到无法添加节点为止,那么这个时候进行第一次比较就可以过滤掉一半的元素,再经历一次比较又可以过滤掉1/4的元素,再经历一次比较就可以过滤掉1/8的元素等等,这样一直循环下去我们就可以发现此时查找元素的时间复杂度为O(logN),但是这里存在一个问题虽然这样的结构能够带来logN的效率,但是该效率是用整齐的结构换过来的,如果在使用的过程中对元素进行插入和删除这种结构就会被破坏,比如说最高的层数为10,如果我要往中间的节点插入一个节点的话这个节点的层数是多少呢?1到10都可以对吧,但是插入之后链表就没办法保持之前的规律(每相邻的节点抬高一层),如果要维持这种对应关系,就必须把新插入的节点后面的所有节点(也包括新插入的节点)重新进行调整,这会让时间复杂度重新蜕化成O(n)。skiplist的设计为了避免这种问题,做了一个大胆的处理,不再严格要求对应比例关系,而是插入一个节点的时候随机出一个层数。这样每次插入和删除都不需要考虑其他节点的层数,这样就好处理多了。
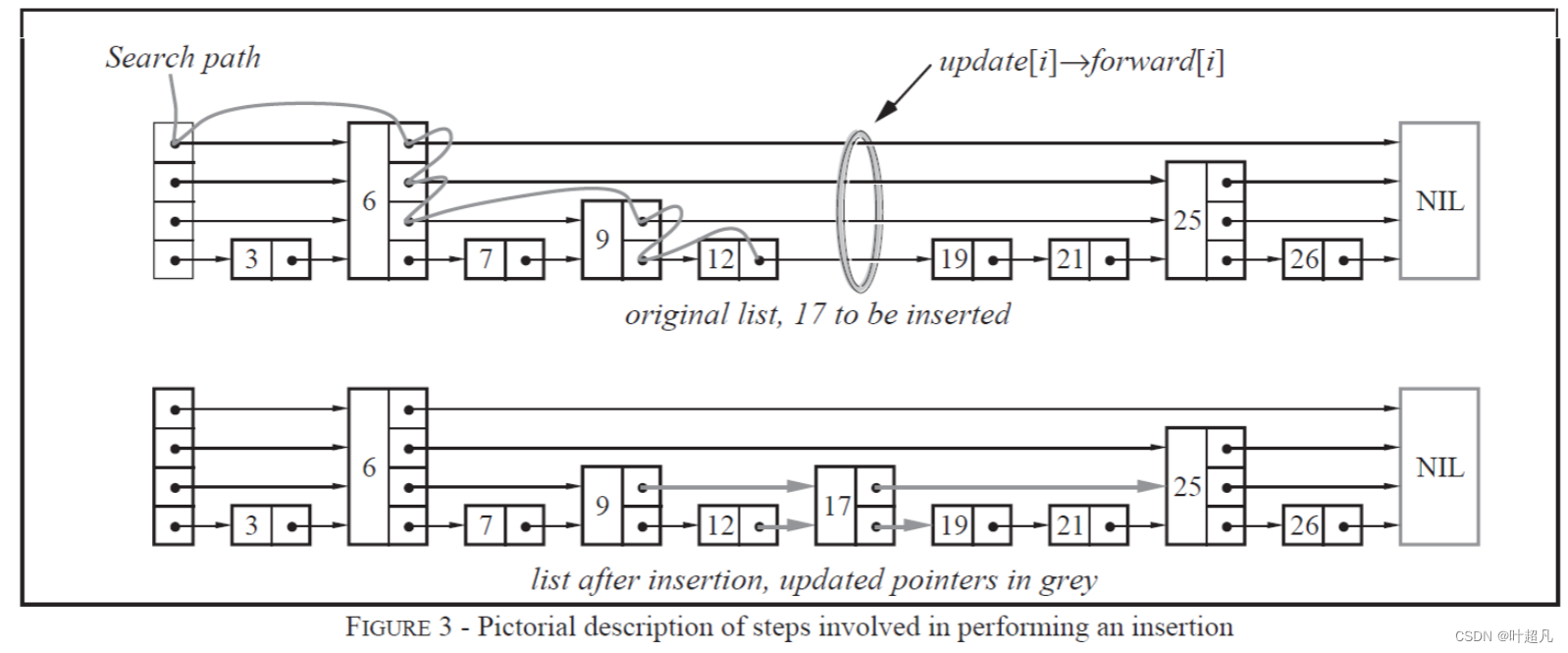
那这里就存在一个问题如果时随机分配层数的话那如何来保证效率呢?随机数有很多很多:1是随机数1w也是随机数,并且还可能出现多个很大的随机数,比如说当前有100个节点但是有99个节点的高度为100,但是我们需要很多高层的节点吗?好像不需要对吧,理论上来说层数越高的节点出现的概率应该越小,所以为了提高跳表的空间效率和时间效率我们给跳表设计一个最大层数maxLevel的限制,其次再设置一个多增加一层的概率P,也就是说每个节点的高度至少为1每升高一层的概率p,那么一个节点的高度为1的概率是:1-P(本来就有一个层高度不增加的概率为1-p)所以高度为1的概率是1-P,同样的道理高度为1增高一层的概率为p不增加的概率为1-p所以层数为二的概率就是p*(1-p),节点层数为3的概率就是p*p*(1-p),这样以此类推就不难发现节点层数越高出现的概率越小:
那么这就是跳表的原理接下来我们来看看如何实现跳表。
跳表的模拟实现
准备工作
首先每个节点的中存在一个变量用来存储数据,然后还需要一堆指针来记录下一个节点的位置,指针的数量不清楚而且又不止一个所以我们可以创建一个vector对象来存储指针,那么这里我们就可以创建一个类来描述指针,该类的构造函数就需要两个参数一个参数表示节点的层数另外一个参数表示节点存储的数据,然后在构造函数里面就对数组进行初始化将每个指针都初始化为空,那么这里的代码如下:
template<class T>
struct ListNode
{typedef ListNode<T> Node;ListNode(T val,int size):_nextV(size,nullptr),_val(val){}T _val;vector<Node*> _nextV;
};
然后在跳表类里面就存储一个指针变量用来记录头结点然后创建另个变量用来记录当前节点的最大层数和增加层数的概率,在构造函数里面将这个指针指向一个新创建的节点,节点的高度为1存储的值为元素的默认构造,并且后面的代码我们要用到随机数这个东西,所以在构造函数里面还得添加一个时间戳,那么这里的代码如下:
template<class T>
class Skiplist
{
public:typedef ListNode<T> Node;Skiplist(){srand(time(0));_head = new Node(T(), 1);}private:Node* _head;int _maxLevel = 32;double _p = 0.5;
};
find函数
find函数是这个类的关键因为这里我们不仅要找到这个元素还得找到直线这个元素的其他节点,比如我们要查找元素21:

在节点21前面存在很多节点指向21,比如说9号节点17号节点19号节点这三个节点都指向节点21,那么find函数不仅要判断21是否存在还得返回指向21号节点的节点,之所以这么做是为了方便后面的insert函数和erase函数,但是这里存在一个问题我们知道了哪个节点指向21,但是不知道是这些节点中的哪个指针指向21?所以这个时候就得将数组中的下表结合起来,因为一个高度的指针只有一个指针指向某个节点,所以我们就可以用数组的下表来进行辅助判断,如果数组中下表为1的元素中记录的节点是9号节点的话就表明9号节点的中下表为1的指针指向了该节点,那么这样find函数不仅可以查询节点是否存在还可以找到哪些位置指向该节点,这样可以方便后面的插入函数和删除函数,那么首先这个函数需要一个T类型的参数,然后返回值是vector类型并且vector中的元素类型是Node*
vector<Node*> find(const T& target)
{}
然后在函数里面就可以创建一个vector,将其大小初始化为头结点的长度,然后创建一个变量level用来存储头结点中数组的个数,因为我们要不停比较节点中的值,所以还得创建一个Node类型的指针用来指向当前寻找的节点,然后就可以创建一个while循环,因为循环的目的是将每一个指向目标节点的节点都记录下来,所以循环结束的条件就是level大于等于0,那么这里代码如下:
vector<Node*> find(const T& target)
{int level = _head->_nextV.size()-1;//这里是下表所以要减一vector<Node*> tmp(level+1,_head);//这里要加一,并且每个元素都指向头结点Node* cur = _head;while (level >= 0){}
}
循环里面我们就要做出判断:当前cur指向的节点的level层指针指向的元素是否小于target,如果小于就将cur指向level层指针指向的元素,如果大于target或者当前的指针指向的元素为空就说明找到了指向插入位置或者要删除元素的前一个节点,那么这个时候就将该节点的地址填入数组中的level下表然后将level的值减减即可,那么这里额度代码如下:
vector<Node*> find(const T& target)
{int level = _head->_nextV.size()-1;//这里是下表所以要减一vector<Node*> tmp(level+1,_head);//这里要加一,并且每个元素都指向头结点Node* cur = _head;while (level >= 0){// 目标值比下一个节点值要大,向右走// 下一个节点是空(尾),目标值比下一个节点值要小,向下走if (cur->_nextV[level] != nullptr && cur->_nextV[level]->_val < target){// 向右走cur = cur->_nextV[level];}else if (cur->_nextV[level] == nullptr || cur->_nextV[level]->_val >= target){// 更新level层前一个tmp[level] = cur;// 向下走level--;}}return tmp;
}
当然这样的find函数还是太难用了,所以我们还是添加一个简化版的find函数,那么这里的思路是一样的我们就直接看代码:
bool search(T target)
{Node* cur = _head;int level = _head->_nextV.size() - 1;while (level >= 0){// 目标值比下一个节点值要大,向右走// 下一个节点是空(尾),目标值比下一个节点值要小,向下走if (cur->_nextV[level] && cur->_nextV[level]->_val < target){// 向右走cur = cur->_nextV[level];}else if (cur->_nextV[level] == nullptr || cur->_nextV[level]->_val > target){// 向下走--level;}else{return true;}}return false;
}
insert函数
当出现重复值时插入可能失败所以insert函数的返回值为bool,函数的参数为T类型
bool insert(T num)
{
}
那么在函数的开始就得创建一个数组用来接收find函数的返回值,然后我们得生成一个随机数用来记录数的高度,那么这里我们还得写一个函数用来随机创建树的高度,那么这里的代码如下:
int RandomLevel()
{size_t level = 1;// rand() ->[0, RAND_MAX]之间while (rand() <= RAND_MAX*_p && level < _maxLevel){++level;}return level;
}
我们知道rand函数生成的数据大小是有范围的,那么我们就可以利用这个范围来生成随机高度,有了这个函数之后我们就可以得到高度,然后new出来节点并将节点的高度设为函数的返回值,那么这里的代码如下:
bool insert(T num)
{vector<Node*> prevV = FindPrevNode(num);int height = RandomLevel();Node* newnode = new Node(num, height);
}
因为插入一个节点之后,可能该节点的高度会刷新整个链表的高度,所以我们得进行判断如果新创建出来的节点高度大于头结点的高度就得对头节点和上面的prevV进行扩长,那么这里就得添加一个if语句:
bool insert(T num)
{vector<Node*> prevV = FindPrevNode(num);int height = RandomLevel();Node* newnode = new Node(num, height);if (height > _head->_nextV.size()){_head->_nextV.resize(height, nullptr);prevV.resize(height, _head);}
}
然后就要将prevV数组中的节点高度个元素的指针指向进行改变,让新插入的节点指向他们之前指向的节点,然后让这些节点指向新插入的节点,比如说下面的图片要插入元素15
插入之后就变成这样:
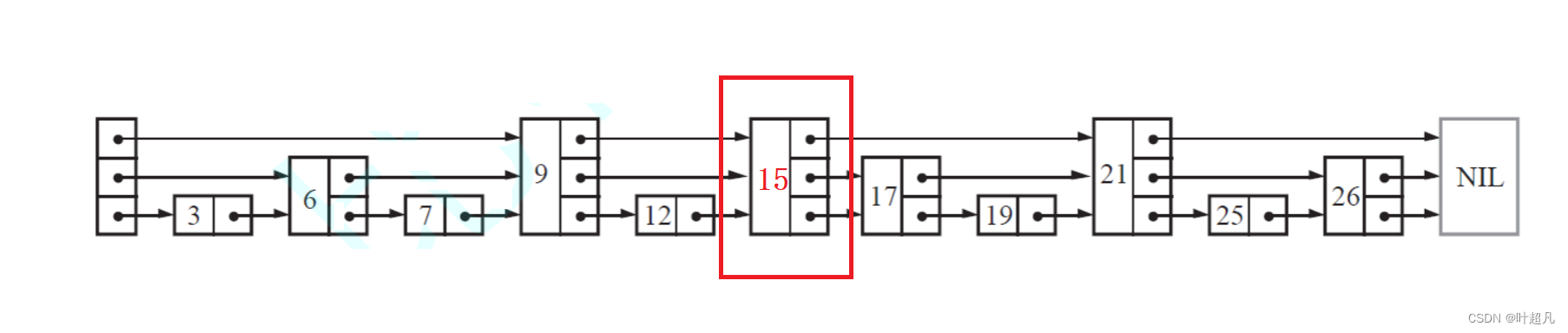
而数组prevV中刚好记录所有指向该位置的节点,那么这里就可以创建一个while循环进行更改,那么完整的代码如下:
bool insert(T num)
{vector<Node*> prevV = find(num);int height = RandomLevel();Node* newnode = new Node(num, height);if (height > _head->_nextV.size()){_head->_nextV.resize(height, nullptr);prevV.resize(height, _head);}for (int i = 0; i < height; i++){newnode->_nextV[i] = prevV[i]->_nextV[i];prevV[i]->_nextV[i] = newnode;}
}
erase函数
erase函数的实现思路也是一样的首先得判断一下当前要删除的元素是否存在如果不存在的话就直接返回false,如果存在的话先创建一个数组和find函数一起记录指向该节点的节点,然后跟insert函数一样修改节点中指针的指向,将指向该节点的指针指向该节点的下一个,那么这里的代码如下:
bool erase(T num)
{vector<Node*> prevV = FindPrevNode(num);// 第一层下一个不是val,val不在表中if (prevV[0]->_nextV[0] == nullptr || prevV[0]->_nextV[0]->_val != num){return false;}else{Node* del = prevV[0]->_nextV[0];// del节点每一层的前后指针链接起来for (size_t i = 0; i < del->_nextV.size(); i++){prevV[i]->_nextV[i] = del->_nextV[i];}delete del;}
}
但是这里存在一个问题,如果将最高节点删除了那头节点是不是也得进行变化呢?所以这里还得查看一下头结点中不为空指针的数量,然后将其长度进行缩小,那么完整的代码如下:
bool erase(T num)
{vector<Node*> prevV = FindPrevNode(num);// 第一层下一个不是val,val不在表中if (prevV[0]->_nextV[0] == nullptr || prevV[0]->_nextV[0]->_val != num){return false;}else{Node* del = prevV[0]->_nextV[0];// del节点每一层的前后指针链接起来for (size_t i = 0; i < del->_nextV.size(); i++){prevV[i]->_nextV[i] = del->_nextV[i];}delete del; }int i = _head->_nextV.size() - 1;while (i >= 0){if (_head->_nextV[i] == nullptr)--i;elsebreak;}_head->_nextV.resize(i + 1);return true;
}
测试
为了方便测试我们可以添加一个打印函数:
void Print()
{Node* cur = _head;while (cur){printf("%2d\n", cur->_val);// 打印每个每个cur节点for (auto e : cur->_nextV){printf("%2s", "↓");}printf("\n");cur = cur->_nextV[0];}
}
然后用下面的代码来进行测试:
int main()
{Skiplist<int> tmp;tmp.insert(11);tmp.insert(5);tmp.insert(6);tmp.insert(12);tmp.insert(2);tmp.insert(3);tmp.insert(7);tmp.insert(17);tmp.insert(19);cout << tmp.search(11) << endl;cout << tmp.search(20) << endl;tmp.erase(11);cout << tmp.search(11) << endl;cout << endl;tmp.Print();return 0;
}
代码的运行结果如下:
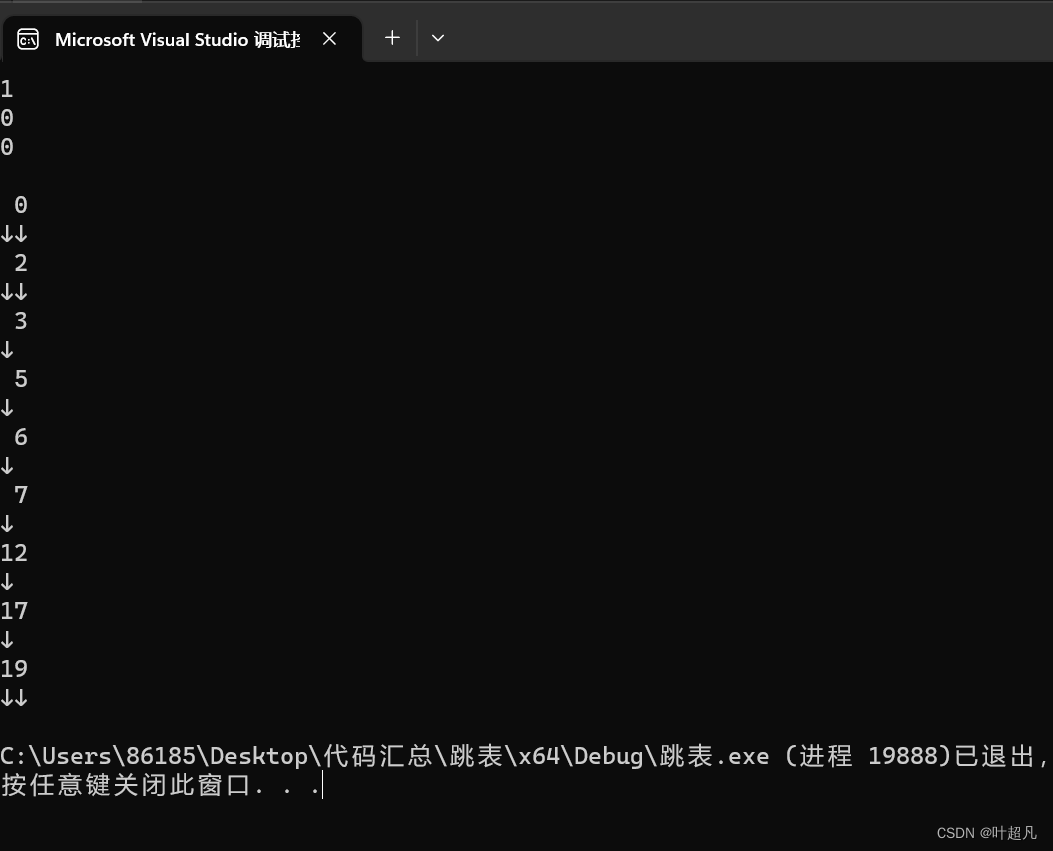
可以看到代码的运行结果符合我们的预期。
效率比较
- skiplist相比平衡搜索树(AVL树和红黑树)对比,都可以做到遍历数据有序,时间复杂度也差不多。skiplist的优势是:a、skiplist实现简单,容易控制。平衡树增删查改遍历都更复杂。b、skiplist的额外空间消耗更低。平衡树节点存储每个值有三叉链,平衡因子/颜色等消耗。skiplist中p=1/2时,每个节点所包含的平均指针数目为2;skiplist中p=1/4时,每个节点所包含的平均指针数目为1.33;
- skiplist相比哈希表而言,就没有那么大的优势了。相比而言a、哈希表平均时间复杂度是O(1),比skiplist快。b、哈希表空间消耗略多一点。skiplist优势如下:a、遍历数据有序b、skiplist空间消耗略小一点,哈希表存在链接指针和表空间消耗。c、哈希表扩容有性能损耗。d、哈希表再极端场景下哈希冲突高,效率下降厉害,需要红黑树补足接力。
相关文章:

数据结构---跳表
目录标题 为什么会有跳表跳表的原理跳表的模拟实现准备工作find函数insert函数erase函数 测试效率比较 为什么会有跳表 在前面的学习过程中我们学习过链表这个容器,这个容器在头部和尾部插入数据的时间复杂度为O(1),但是该容器存在一个缺陷就是不管数据…...

为什么Tomcat的NIO在读取body时要模拟阻塞?
文章首发地址 Tomcat的NIO完全可以以非阻塞方式处理IO,为什么在读取body部分时要模拟阻塞呢?在Tomcat的NIO读取HTTP请求时,为了保证请求的正确性和可靠性,需要模拟阻塞模式,这是因为servlet规范里定义了ServletInputSt…...

26 | 谷歌应用APP数据分析
基于kaggle公开数据集,对谷歌应用市场的APP情况进行数据探索和分析。 from kaggle: https://www.kaggle.com/lava18/google-play-store-apps 分析思路: 0、数据准备 1、数据概览 2、种类对Rating的影响 3、定价策略 4、因素相关性分析 5、用户评价 6、总结 0、数据准备 (…...

BFS 五香豆腐
题目描述 经过谢老师n次的教导,dfc终于觉悟了——过于腐败是不对的。但是dfc自身却无法改变自己,于是他找到了你,请求你的帮助。 dfc的内心可以看成是5*5个分区组成,每个分区都可以决定的的去向,0表示继续爱好腐败&…...

opencv实战项目 手势识别-手势控制键盘
手势识别是一种人机交互技术,通过识别人的手势动作,从而实现对计算机、智能手机、智能电视等设备的操作和控制。 1. opencv实现手部追踪(定位手部关键点) 2.opencv实战项目 实现手势跟踪并返回位置信息(封装调用&am…...

1.作用域
1.1局部作用域 局部作用域分为函数作用域和块作用域。 1.函数作用域: 在函数内部声明的变量只能在函数内部被访问,外部无法直接访问。 总结: (1)函数内部声明的变量,在函数外部无法被访问 (2)函数的参数也是函数内部的局部变量 (3)不同函数…...

黑马B站八股文学习笔记
视频地址:https://www.yuque.com/linxun-bpyj0/linxun/vy91es9lyg7kbfnr 大纲 基础篇 基础篇要点:算法、数据结构、基础设计模式 1. 二分查找 要求 能够用自己语言描述二分查找算法能够手写二分查找代码能够解答一些变化后的考法 算法描述 前提&a…...

前端常用的上传下载文件的几种方式,直接上传、下载文件,读取.xlsx文件数据,导出.xlsx数据
一、通过调用接口下载文件 const onExport async () > {try {let res await axios.request({method: POST,url: 请求地址,responseType: blob,params: { data: null },headers: { Authorization: Bearer UserModule.token },//看看请求是否需要token});let reader new…...
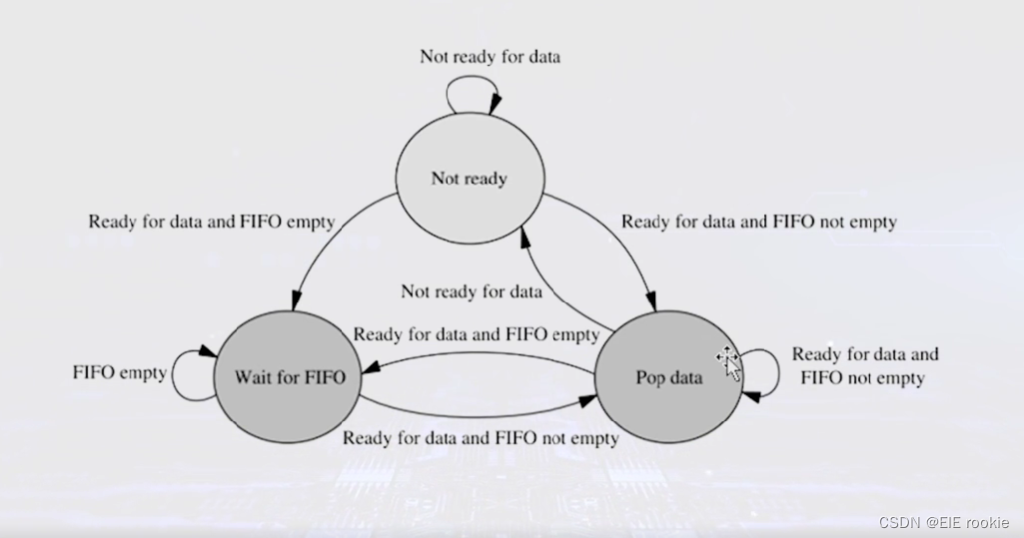
FPGA应用学习笔记--时钟域的控制 亚稳态的解决
时钟域就是同一个时钟的区域,体现在laways语句边缘触发语句中,设计规模增大就会导致时钟不同步,有时差,就要设计多时钟域。 会经过与门的延时产生的新时钟域,这种其实不推荐使用,但在ascl里面很常见 在处理…...
AirServer是什么软件,手机屏幕投屏电脑神器
什么是 AirServer? AirServer 是适用于 Mac 和 PC 的先进的屏幕镜像接收器。 它允许您接收 AirPlay 和 Google Cast 流,类似于 Apple TV 或 Chromecast 设备。AirServer 可以将一个简单的大屏幕或投影仪变成一个通用的屏幕镜像接收器 ,是一款…...

如何使用 AT+WEBSERVER 指令实现自定义的 Webserver html 网页配网
开启 AT 固件中的 Webserver 指令和 FS 指令支持 乐鑫官网发布的默认通用 AT 固件不支持 webserver 配网功能, 需要用户自己搭建 esp-at 环境,并在 sdkconfig 中开启 webserver AT 指令 和 FS 指令的支持, 如下图所示: 测试 AT 固…...
期权定价模型系列【4】—期权组合的Delta-Gamma-Vega中性
期权组合的Delta-Gamma-Vega中性 期权组合构建时往往会进行delta中性对冲,在进行中性对冲后,期权组合的delta敞口为0,此时期权组合仍然存在gamma与vega敞口。因此研究期权组合的delta-gamma-vega敞口中性是有必要的。 本文旨在对delta-gamma-…...

k8sday02
第四章 实战入门 本章节将介绍如何在kubernetes集群中部署一个nginx服务,并且能够对其进行访问。 Namespace Namespace是kubernetes系统中的一种非常重要资源,它的主要作用是用来实现多套环境的资源隔离或者多租户的资源隔离。 默认情况下&…...
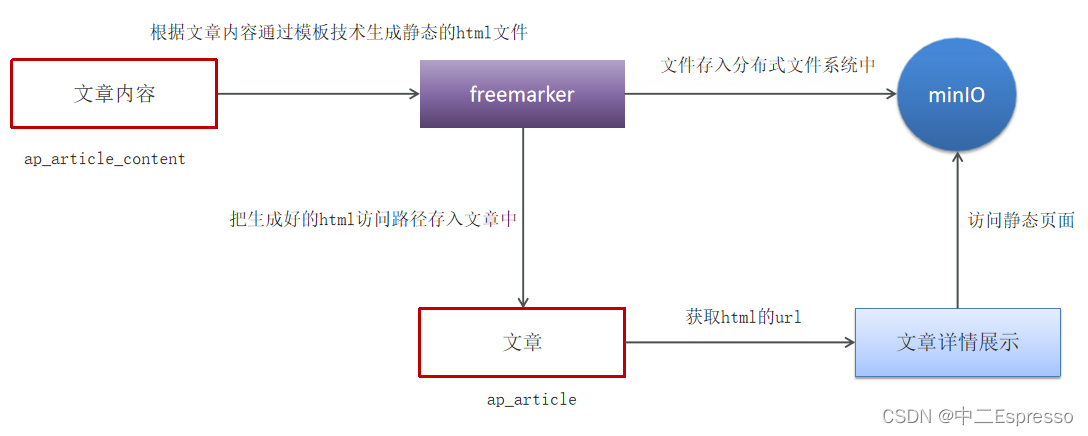
黑马头条项目学习--Day2: app端文章查看,静态化freemarker,分布式文件系统minIO
app端文章 Day02: app端文章查看,静态化freemarker,分布式文件系统minIOa. app端文章列表查询1) 需求分析2) 实现思路 b. app端文章详细1) 需求分析2) Freemarker概述a) 基础语法种类b) 集合指令(List和Map)c) if指令d) 运算符e) 空值处理f) …...
特语云用Linux和MCSM面板搭建 我的世界基岩版插件服 教程
Linux系统 用MCSM和DockerWine 搭建 我的世界 LiteLoaderBDS 服务器 Minecraft Bedrock Edition 也就是我的世界基岩版,这是 Minecraft 的另一个版本。Minecraft 基岩版可以运行在 Win10、Android、iOS、XBox、switch。基岩版不能使用 Java 版的服务器,…...

2023.8
编译 make install 去掉 folly armv8-acrc arrow NEON 相关链接 https://blog.csdn.net/u011889952/article/details/118762819 这里面的方案二,我之前也是用的这个 https://blog.csdn.net/zzhongcy/article/details/105512565 参考的此博客 火焰图 https://b…...
CSV文件编辑器——Modern CSV for mac
Modern CSV for Mac是一款功能强大、操作简单的CSV文件编辑器,适用于Mac用户快速、高效地处理和管理CSV文件。Modern CSV具有直观的用户界面,可以轻松导入、编辑和导出CSV文件。它支持各种功能,包括排序、过滤、查找和替换,使您能…...
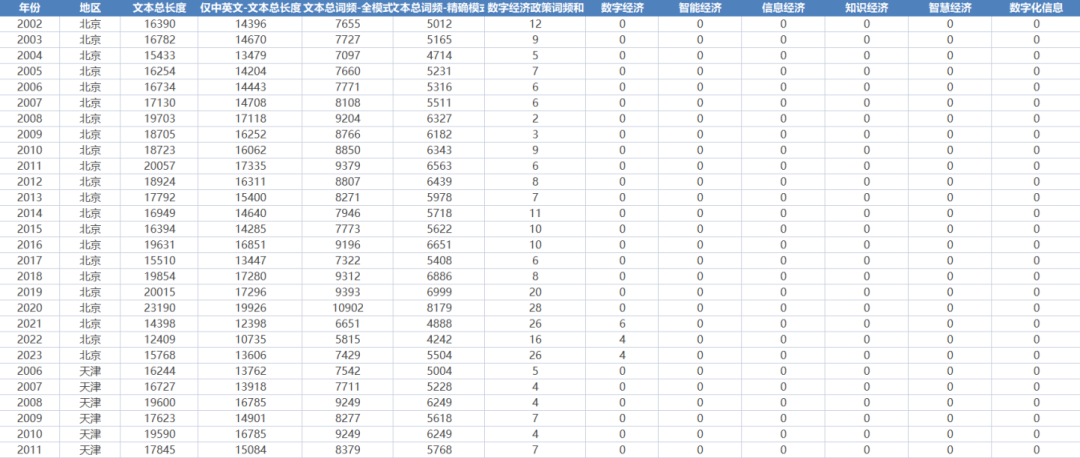
全国各地区数字经济工具变量-文本词频统计(2002-2023年)
数据简介:本数据使用全国各省工作报告,对其中数字经济相关的词汇进行词频统计,从而构建数字经济相关的工具变量。凭借数字经济政策供给与数字经济发展水平的相关系数的显著性作为二者匹配程度的划分依据,一定程度上规避了数字经济…...

MacOS安装RabbitMQ
官网地址: RabbitMQ: easy to use, flexible messaging and streaming — RabbitMQ 一、brew安装 brew update #更新一下homebrew brew install rabbitmq #安装rabbitMQ 安装结果: > Caveats > rabbitmq Management Plugin enabled by defa…...
关于selenium 元素定位的浅度解析
一、By类单一属性定位 元素名称 描述 Webdriver API id id属性 driver.find_element(By.ID, "id属性值") name name属性 driver.find_element(By.NAME, "name属性值") class_name class属性 driver.find_element(By.CLASS_NAME, "class_na…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...
