(文章复现)基于灰狼算法(GWO)的交直流混合微网经济调度matlab代码
参考文献:
[1]高瑜,黄森,陈刘鑫等.基于改进灰狼算法的并网交流微电网经济优化调度[J].科学技术与工程, 2020,20(28):11605-11611.
[2]邓长征,冯朕,邱立等.基于混沌灰狼算法的交直流混合微网经济调度[J].电测与仪表, 2020, 57(04):99-107.
这两篇文章不管是从模型、原理、求解方法还是算例分析上看,都非常相似,鉴于文章两篇文章的作者单位没有重合,肯定是两位不同的作者在不同的时间灵感爆发,提出了相同的idea(甚至文献1中目标函数中成本只有4项,但算例分析部分和文献2一样有5项成本),证明了学术论文的可重复性。分析表明,这两篇文章绝对没有谁照搬谁的情况,也不可能是两个人抄了同一篇英文文献,更不可能是找了同一家论文代写机构然后被坑了。
综上所示,这篇博客就是对上面两篇不同文章中提到的一种相同的方法进行复现,以实现本人水一篇博客的目的。
1.基本原理
交直流混合微电网运行方式分为孤岛运行方式和并网运行方式,在本次研究中主要考虑并网情况下交直流混合微电网的经济优化调度。交直流混合微电网分为交流侧和直流侧,交流侧与外部大电网互联。交流侧包含交流母线、交流微电源和交流负荷; 直流侧包含直流母线、直流微电源和直流负荷。具体结构如图 1所示。
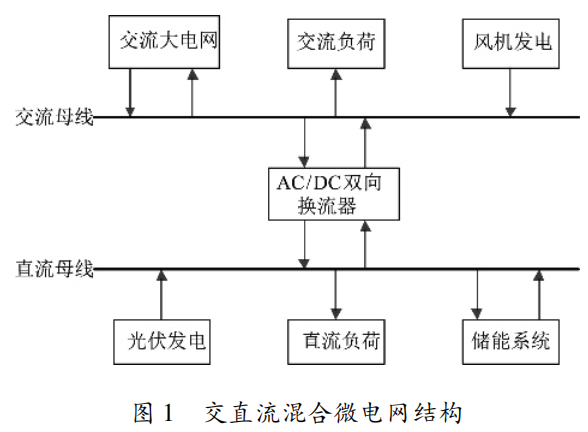
交直流混合微电网的主要运行方式有4种:
( 1) 满足交流侧和直流侧功率平衡,交流侧和直流侧的微电源相应满足交流负荷和直流负荷的供电需求;
( 2) 通过AC /DC 双向换流器使交流侧和直流侧功率交互,交流侧和直流侧互为补充,满足微网内交流负荷和直流负荷总的供电需求;
( 3) 直流侧储能系统参与微电网削峰填谷和平抑功率,当微网中微电源总出力大于负荷所需供电要求时; 储能系统充电,反之则储能系统放电;
( 4) 当微网中微电源和储能系统在某一时刻的出力不足以满足微网中负荷的需求时,向交流大电网购电; 反之则向大电网售电。储能系统和换流系统在以上运行方式中有重要的作用,因此在建立交直流混合微电网经济优化调度的经济模型中应考虑储能损耗和换流成本。
1.1目标函数


交流微电网内器件维修保养费用 F2 为



1.2约束条件





2.改进灰狼算法求解
2.1基本灰狼算法
来自澳大利亚的研究者 Mirjalili 于2014年提出一种新型群体智能算法——灰狼算法( grey wolf optimizer,GWO) [12]。灰狼算法通过模拟灰狼狼群在捕食过程中的特征及狼群等级制度,通过灰狼对猎物不停地搜索追寻,不断更新猎物所处的位置,最终灰狼成功捕捉猎物。在 GWO 算法中,将狼群按照等级由高到低分为 α 狼、β 狼、δ 狼和其余狼群个体 ω,灰狼的等级越高,其自身适应度越好,猎物的位置则对应全局最优解。α 狼为头狼,在狼群中起领导及决策作用; β 狼为头狼候选,在狼群中反馈信息给 α 狼; δ 狼负责对 ω 狼群的统领; ω 狼对猎物实施搜寻与追捕。狼群捕食过程首先要包围猎物,灰狼需要知道自身与猎物的距离大小,然后根据自身与猎物的距离来调整自己的位置。灰狼包围猎物的数学公式为

在狼群捕食过程中,α 狼、β 狼、δ 狼与猎物之间的距离可由式( 25) ~ 式( 27) 计算。由于 α 狼、β狼、δ 狼在狼群中等级制度,这意味着它们的适应度更好,从而离猎物的距离更近,ω 狼根据 α 狼、β 狼、 δ 狼的位置向猎物靠近,ω 狼朝向 α 狼、β 狼、δ 狼前进的方向与前进步长分别可由式( 28) ~ 式( 30) 计算。

灰狼算法的流程图如图 2 所示。
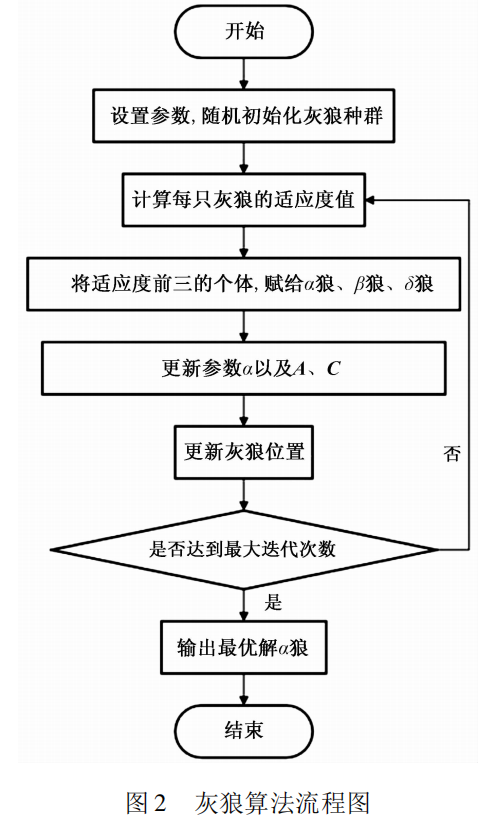
2.2改进灰狼算法
均衡 GWO 的全局搜索能力和局部搜索能力,是 GWO 能否取得高寻优性能的关键因素。当| A | > 1 时,灰狼群体将扩大包围圈,以寻找更让好的猎物,此时对应于全局搜索; 当 | A | < 1 时,灰狼群体将收缩包围圈,从而对猎物完成最后的攻击行为,此时对应于局部精确搜索[13]。因此 GWO 的全局搜索能力和局部搜索能力与 | A | 的取值之间有着极大关联,另外根据式( 23) 可知 | A| 的取值也与收敛因子 a 的取值紧密相关。由于原始 GWO 的收敛因子是线性的,且收敛因子 a 从 2 线性递减至 0,这种线性递减策略不能完全体现出实际的优化搜索过程。因此,引进一种基于非线性变化的收敛因子更新公式:

采取非线性变化的收敛因子在寻优初始阶段,a 衰减程度低,这时候,算法的全局寻优能力较强,能够搜索到更好的全局最优解;寻优末尾阶段,a 衰减程度高,这时候,算法的局部寻优能力较强,能够搜索到更好的局部最优解。这种基于非线性变化的收敛因子可以更够更好地均衡 GWO 的全局寻优能力和局部寻优能力,从而获得精度更好的解。
3.编程思路分析
3.1相关参数和决策变量定义
表1 相关参数的定义

表2 决策变量的定义

3.2编程思路
根据对文献内容的解读,可以设计下面的编程思路:
步骤1:输入所需数据
这一步比较简单。算例分析用到的大部分数据可以从原文中找到,其他数据可以自己假设一下。然后将所有需要的数据,按照表1的定义格式输入即可。
步骤2:灰狼算法的实现
实现基本的灰狼优化算法和改进灰狼优化算法,并使用文中提到的四个测试函数进行验证,两篇文章中对灰狼算法改进各不相同,一个是改进了收敛因子,一个是改进了初始化策略,这篇博客中的代码是将两种改进策略结合起来。以Sphere函数为例,基本灰狼优化算法和改进灰狼优化算法的对比如下(优化问题维度取10,种群数和最大迭代次数分别为200,100):
基本灰狼算法的运行结果:
最优解:x=1.6921e-13 9.8087e-15 -1.527e-13 -3.2711e-15 -3.2045e-14 -7.4947e-14 1.5045e-14 1.6444e-14 -2.0382e-14 2.4686e-14
最优函数值=6.0224e-26
改进灰狼算法的运行结果:
最优解:x=1.5078e-17 -1.7022e-16 1.3285e-18 3.5724e-17 2.0807e-16 3.5095e-17 -2.8155e-16 2.14e-16 1.5832e-16 -9.8643e-17
最优函数值=2.3486e-31
仅针对Sphere函数而言,改进灰狼算法的效果要更好一些。
步骤3:将灰狼算法用于微网调度问题
如表2所示,原文中共包含3个决策变量,都是1×24的变量,需要将其组合成一个1×72的变量,便于使用灰狼算法求解,也就意味中文中涉及的优化问题维度为72,具体变量设置如下:
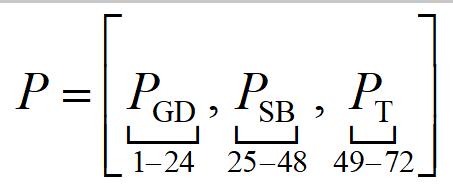
智能优化算法中对于约束条件的处理有很多种形式,我在代码中参考这篇文章给的罚函数法进行处理:粒子群算法求解带约束优化问题 - 知乎。
另外,如果只遵循上下限约束生成初始种群,可能导致生成的种群中大部分甚至全部的个体都是不满足约束的,因此生成种群和更新种群时,还是要满足一定规则,使得生成的种群尽可能都满足约束。
步骤4:输出运行结果
参考文中的图表的格式,输出结果即可。
4.Matlab代码
%% 清除变量
clc
clear
close all
warning off%% 设置种群参数
sizepop = 200; % 初始种群个数
dim = 10; % 空间维数
ger = 100; % 最大迭代次数
x_max = 100*ones(1,dim); % 位置上限
x_min = -100*ones(1,dim); % 位置下限%% 种群初始化
pop = x_min + rand(sizepop,dim).*(x_max-x_min); % 初始化种群
fitness = zeros(1,sizepop); % 所有个体的适应度
for k = 1:sizepopfitness(k) = Sphere(pop(k,:));
end% 初始化Alpha、Beta、Delta狼群
[SortFitness,Index] = sort(fitness);
A_pop = pop(Index(1),:); % 初始化α狼群
A_fitness = SortFitness(1); % 初始化α狼群适应度
B_pop = pop(Index(2),:); % 初始化β狼群
B_fitness = SortFitness(2); % 初始化β狼群适应度
D_pop = pop(Index(3),:); % 初始化δ狼群
D_fitness = SortFitness(3); % 初始化δ狼群适应度
history = zeros(1,ger); % 历史最优适应度值
%% 迭代求最优解
iter = 1;
while iter <= gera = 2 - iter*(2/ger); % 线性调整a的值for k = 1:sizepop% 1.根据Alpha狼群更新位置X1r1 = rand;r2 = rand;A1 = 2*a*r1 - a;C1 = 2*r2;D_A = abs(C1*A_pop - pop(k,:));X1 = A_pop - A1*D_A;% 2.根据Beta狼群更新位置X2r1 = rand;r2 = rand;A2 = 2*a*r1 - a;C2 = 2*r2;D_B = abs(C2*B_pop - pop(k,:));X2 = B_pop - A2*D_B;% 3.根据Delta狼群更新位置X3r1 = rand;r2 = rand;A3 = 2*a*r1 - a;C3 = 2*r2;D_D = abs(C3*D_pop - pop(k,:));X3 = D_pop - A3*D_D;% 4.更新后的狼群位置pop(k,:) = (X1+X2+X3)/3;% 修复越限的狼群位置pop(k,pop(k,:) > x_max) = x_max(pop(k,:) > x_max);pop(k,pop(k,:) < x_min) = x_max(pop(k,:) < x_min);% 更新狼群的适应度fitness(k) = Sphere(pop(k,:));end% 更新Alpha、Beta、Delta狼群位置[SortFitness,Index] = sort(fitness);A_pop = pop(Index(1),:); % 初始化α狼群A_fitness = SortFitness(1); % 初始化α狼群适应度B_pop = pop(Index(2),:); % 初始化β狼群B_fitness = SortFitness(2); % 初始化β狼群适应度D_pop = pop(Index(3),:); % 初始化δ狼群D_fitness = SortFitness(3); % 初始化δ狼群适应度history(iter) = A_fitness;iter = iter+1;
end%% 画图
disp(['最优解:x=',num2str(A_pop)])
disp(['最优函数值=',num2str(A_fitness)])
plot(history,'linewidth',1)
ylabel('最优适应度值')
xlabel('迭代次数')
%% 适应度函数
function fitness = Sphere(pop)
fitness = sum(pop.^2);
end运行结果如下:
最优解:x=-2.7836e-14 1.1833e-13 2.0262e-13 1.0821e-14 -2.534e-14 6.7367e-14 -7.4143e-14 -1.6845e-13 -1.5746e-13 3.9423e-14
最优函数值=1.2135e-25
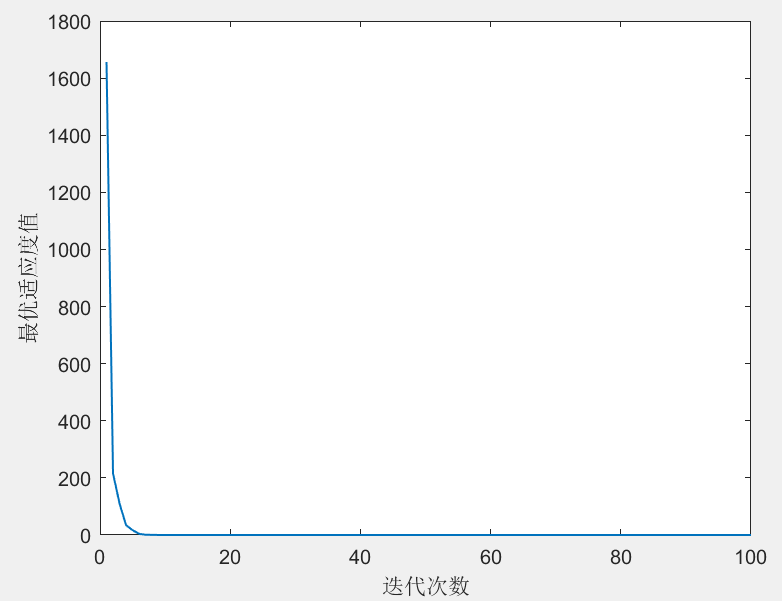
以上仅为基本灰狼算法求解Sphere函数最优解的matlab代码(优化问题维度取10,种群数和最大迭代次数分别为200,100),完整论文复现的matlab代码可以从这个链接获取:
基于灰狼算法(GWO)的交直流混合微网经济调度matlab代码
5.运行结果分析
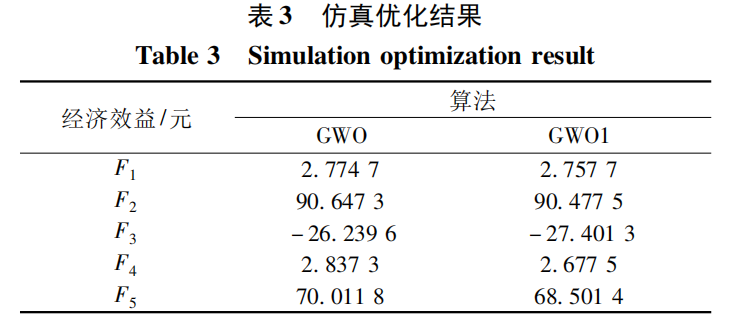
文献结果和复现结果对比如下:
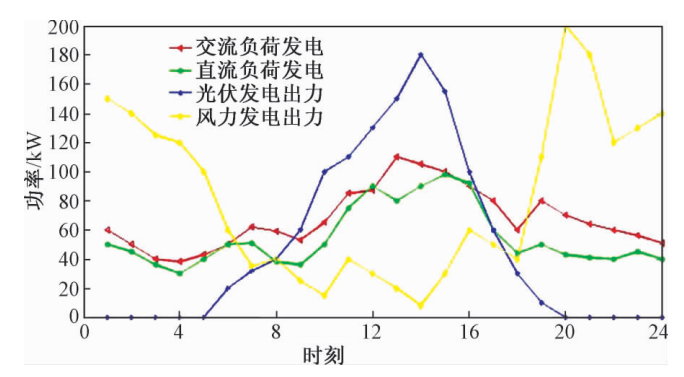
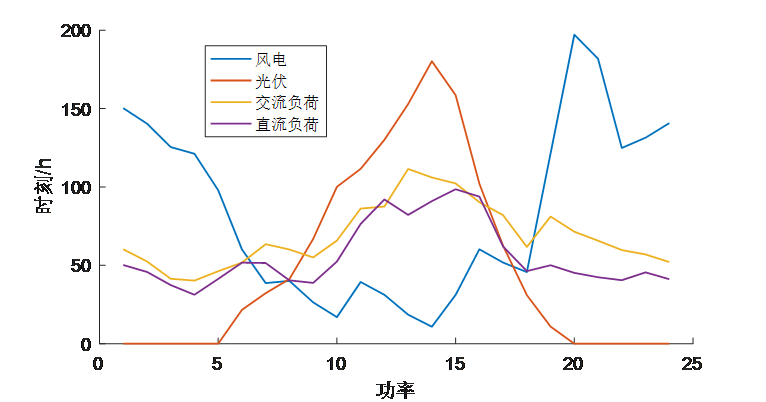
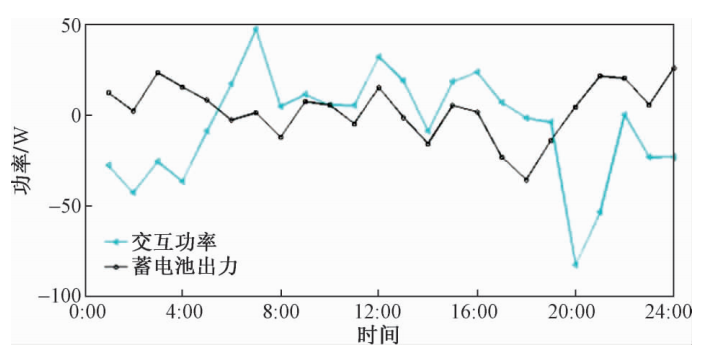
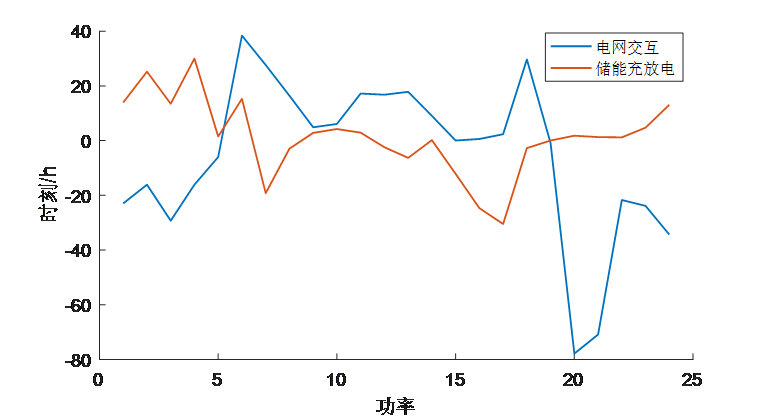
GWO算法改进前后的对比,改进GWO算法险胜:

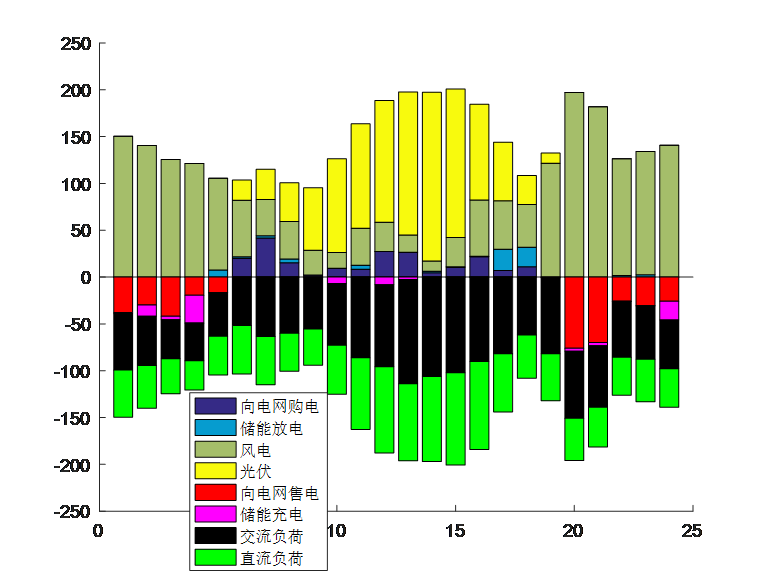
 运行结果画成条形图稍微好看一些:
运行结果画成条形图稍微好看一些:
相关文章:

(文章复现)基于灰狼算法(GWO)的交直流混合微网经济调度matlab代码
参考文献: [1]高瑜,黄森,陈刘鑫等.基于改进灰狼算法的并网交流微电网经济优化调度[J].科学技术与工程, 2020,20(28):11605-11611. [2]邓长征,冯朕,邱立等.基于混沌灰狼算法的交直流混合微网经济调度[J].电测与仪表, 2020, 57(04):99-107. 这两篇文章不管是从模型、…...

【Kubernetes】Kubernetes的调度
K8S调度 一、Kubernetes 调度1. Pod 调度介绍2. Pod 启动创建过程3. Kubernetes 的调度过程3.1 调度需要考虑的问题3.2 具体调度过程 二、影响kubernetes调度的因素1. nodeName2. nodeSelector3. 亲和性3.1 三种亲和性的区别3.2 键值运算关系3.3 节点亲和性3.4 Pod 亲和性3.5 P…...

题目:2511.最多可以摧毁的敌人城堡数量
题目来源: leetcode题目,网址:2511. 最多可以摧毁的敌人城堡数目 - 力扣(LeetCode) 解题思路: 顺序遍历数组,记录上一个我军城堡和没有城堡的位置。当碰到空位置时,若上一次更新的…...

22 | 书籍推荐数据分析
import numpy as np import pandas as pd import seaborn as sns import matplotlib.pyplot as plt from sklearn.cluster import KMeans from sklearn import neighbors from sklearn.model_selection import train_test_split from sklearn.preprocessing import...

vscode extension 怎么区分dev prod
开发模式注入环境变量 使用vsode 提供的api...

Java学习手册——第一篇Java简介
今后Java学习手册就来给大家梳理JavaSE的基础知识啦, 除了这个专栏我们还有其他专栏:前端、安全、后端等。 希望大家可以在这里一起讨论学习哟~ Java学习手册——第一篇Java简介 1. Java基础知识2. Java能干嘛3. Java基础环境搭建 1. Java基础知识 出生…...
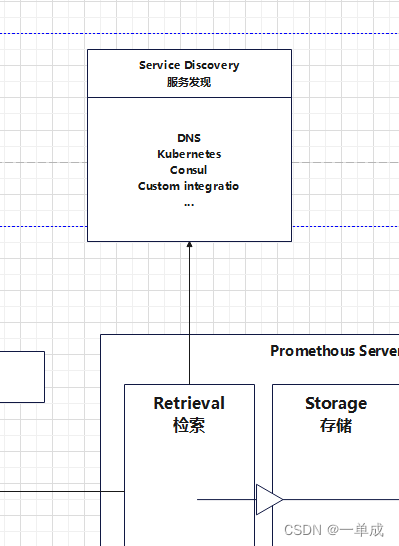
Prometheus流程图(自绘)-核心组件-流程详解
阿丹手绘流程图:图片可能有点小查看的时候放大看看哈! prometheus核心组件 prometheus server Prometheus Server是Prometheus组件中的核心部分,负责实现对监控数据的获取,存储以及查询。Prometheus Server可以通过静态配置管理…...

回归模型常见评估指标mae,mse,rmse
文章目录 MAE(平均绝对误差)计算公式sklearn实现numpy实现mse(均方误差)计算公式sklearn实现numpy实现rmse(均方根误差)计算公式sklearn实现MAE(平均绝对误差) 计算公式 MAE ( y ,...

服务器数据恢复-断电导致ext4文件系统文件丢失的数据恢复案例
服务器数据恢复环境: 一台服务器挂载一台存储设备,存储中划分一个Lun;服务器操作系统是Linux centos,EXT4文件系统。 服务器故障&分析: 意外断电导致服务器操作系统无法启动,系统在修复后可以正常启动&…...

链表(基础详解、实现、OJ笔试题)
文章目录 🧚什么是链表(链表概念及分类)链表分类单链表和双链表的区别 🚴♂️单链表、双向链表的实现单链表的实现双向链表的实现 🍉链表经典OJ笔试题反转单链表移除链表元素合并两个有序链表链表分割链表的中间结点…...
W5100S-EVB-PICO作为TCP Client 进行数据回环测试(五)
前言 上一章我们用W5100S-EVB-PICO开发板通过DNS解析www.baidu.com(百度域名)成功得到其IP地址,那么本章我们将用我们的开发板作为客户端去连接服务器,并做数据回环测试:收到服务器发送的数据,并回传给服务…...
大数据-玩转数据-Redis 安装与使用
一、说明 大多数企业都是基于Linux服务器来部署项目,而且Redis官方也没有提供Windows版本的安装包。因此课程中我们会基于Linux系统来安装Redis. 此处选择的Linux版本为CentOS 7. Redis的官方网站地址:http://download.redis.io/releases 二、下载 m…...

实时指标-1日留存率
2个DWD层 登录→kafka注册→kafka1个DWS 弄2条流,从kafka读取数据将昨日注册数据存到状态中,TTL为2天,存到map状态中,key为注册日期,value为set,存储注册的uid将登录流和注册流进行连接来一条登录数据&…...

【玩转23种Java设计模式】行为型模式篇:责任链模式
软件设计模式(Design pattern),又称设计模式,是一套被反复使用、多数人知晓的、经过分类编目的、代码设计经验的总结。使用设计模式是为了可重用代码、让代码更容易被他人理解、保证代码可靠性、程序的重用性。 汇总目录链接&…...

【C#】获取电脑CPU、内存、屏幕、磁盘等信息
通过WMI类来获取电脑各种信息,参考文章:WMI_04_常见的WMI类的属性_wmi scsilogicalunit_fantongl的博客-CSDN博客 自己整理了获取电脑CPU、内存、屏幕、磁盘等信息的代码 #region 系统信息/// <summary>/// 电脑信息/// </summary>public p…...

途乐证券-最准确的KDJ改良指标?
KDJ目标是技术剖析的一种重要目标之一,它是利用随机目标(%R)发展而来的,是一种反映商场超买和超卖状况的买卖目标。KDJ目标由快线(K线)、慢线(D线)和随机值(J线ÿ…...
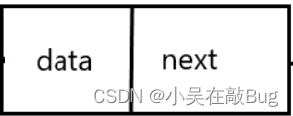
数据结构——线性表
文章目录 线性表的定义和基本操作顺序表线性表的链式表示 线性表的定义和基本操作 线性表是具有相同数据类型的(n≥0)个数据元素的有限序列,其中n为表长,当n0时线性表是一个空表。若用L命名线性表,则其中一般表示为:L(a1,a2,a3, …...
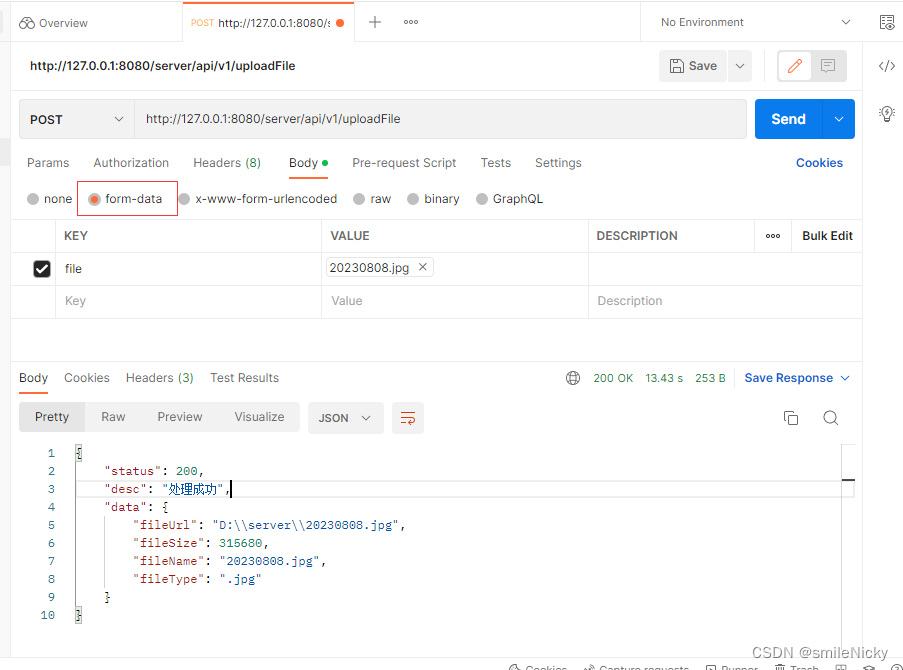
SpringBoot系列之基于Jersey实现文件上传API
前言 JAX-RS:JAX-RS是可以用可以用于实现RESTFul应用程序的JAVA API,给开发者提供了一系列的RESTFul注解Jersey:是基于JAX-RX API的实现框架,用于实现RESTful Web 服务的开源框架。 JAX-RX常用的注解: javax.ws.rs.Pa…...

【LangChain】Prompts之示例选择器
LangChain学习文档 【LangChain】向量存储(Vector stores)【LangChain】向量存储之FAISS【LangChain】Prompts之Prompt templates【LangChain】Prompts之自定义提示模板【LangChain】Prompts之示例选择器 概要 如果您有大量示例,您可能需要选择要包含在提示中的哪…...

Neo4j之CREATE基础
在 Neo4j 中,CREATE 语句用于创建节点、关系以及节点属性。 创建节点: CREATE (p:Person {name: John, age: 30});这个查询会创建一个具有 "Person" 标签的节点,节点属性包括 "name" 和 "age"。 创建带有关…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
