E. Maximum Monogonosity
You are given an array aa of length nn and an array bb of length nn. The cost of a segment [l,r][l,r], 1≤l≤r≤n1≤l≤r≤n, is defined as |bl−ar|+|br−al||bl−ar|+|br−al|.
Recall that two segments [l1,r1][l1,r1], 1≤l1≤r1≤n1≤l1≤r1≤n, and [l2,r2][l2,r2], 1≤l2≤r2≤n1≤l2≤r2≤n, are non-intersecting if one of the following conditions is satisfied: r1<l2r1<l2 or r2<l1r2<l1.
The length of a segment [l,r][l,r], 1≤l≤r≤n1≤l≤r≤n, is defined as r−l+1r−l+1.
Find the maximum possible sum of costs of non-intersecting segments [lj,rj][lj,rj], 1≤lj≤rj≤n1≤lj≤rj≤n, whose total length is equal to kk.
Input
Each test consists of multiple test cases. The first line contains a single integer tt (1≤t≤1000)(1≤t≤1000) — the number of sets of input data. The description of the test cases follows.
The first line of each test case contains two integers nn and kk (1≤k≤n≤30001≤k≤n≤3000) — the length of array aa and the total length of segments.
The second line of each test case contains nn integers a1,a2,…,ana1,a2,…,an (−109≤ai≤109−109≤ai≤109) — the elements of array aa.
The third line of each test case contains nn integers b1,b2,…,bnb1,b2,…,bn (−109≤bi≤109−109≤bi≤109) — the elements of array bb.
It is guaranteed that the sum of nn over all test case does not exceed 30003000.
Output
For each test case, output a single number — the maximum possible sum of costs of such segments.
我比赛时写的是o(nk^2) 的比较常规的转移
dp[n1][k1]=max(dp[n1−1][k1],dp[n1−l][k1−l]+f(n1−l+1,n1),1≤l≤k1)
看别人写之后才发现题目太妙了
首先我们不要把目光光顾着所有个区间,你去看方程的含义
其实化简出来有4中不同的方程
bl-ar+br-al
ar-bl+br-al
ar-bl+al-br
bl-ar+al-br
那bl,al来说有4种不同的状态(1,1),(1,-1),(-1,1),(-1,-1)
因为bl和ar相对应,al和bl相对应,那么br,br的状态恰好和ar,al的相反
所有整个方程有4种状态
那我们怎么知道要用哪种状态呢
我们用dp[4010][4010][5]来存储
dp[i][j][k]--》i表示当前到达第i位,j表示当前取j个元素,k(0~3)用状态压缩表示当第j个元素取al和bl的状态以及前面i-1位中取j-1个元素的最佳状态的和,k(4)表示当前取第i位取j个元素的最佳状态
因为我们上面说你知道ar,al的状态就能知道br,bl的状态:比如bl,al=(1,-1)则br,ar=(1,-1)
因为所有你通过枚举b就能知道当前的最大值
#include<iostream>
#include<algorithm>
#include<numeric>//accumulate(be,en,0)
#include<cstring>//rfind("string"),s.find(string,begin)!=s.npos,find_first _of(),find_last_of()
#include<string>//to_string(value),s.substr(int begin, int length);
#include<cstdio>
#include<cmath>
#include<vector>//res.erase(unique(res.begin(), res.end()), res.end()),reverse(q.begin(),q.end()),vector<int>().swap(at[mx])
#include<queue>//priority_queue(big) /priority_queue<int, vector<int>, greater<int>> q(small)
#include<stack>
//#include<map>//unordered_map
#include<set>//iterator,insert(),erase(),lower(>=)/upper_bound(>)(value)/find()return end()
#include<unordered_map>
#include<unordered_set>
#include<bitset>//size,count(size of 1),reset(to 0),any(have 1?)
//#include<ext/pb_ds/assoc_container.hpp>//gp_hash_table
//#include<ext/pb_ds/hash_policy.hpp>
//using namespace __gnu_pbds;
#define int long long//__int128 2^127-1(GCC)
#define PII pair<int,int>
using namespace std;
const int inf = 0x3f3f3f3f3f3f3f3f, N = 3000 + 5, mod = 1e9 + 7;
int dp[N][N][5];
signed main()
{ios_base::sync_with_stdio(0); cin.tie(0), cout.tie(0);int T;cin >> T;while (T--) {int n, k;cin >> n >> k;vector<int>a(n), b(n);for (int& x : a) cin >> x;for (int& x : b) cin >> x;for (int i = 0; i < n + 1; i++) {for (int j = 0; j <= k; j++) {fill(dp[i][j], dp[i][j] + 5, -inf);//最开始初始化为负无穷}}dp[0][0][4] = 0;//第0位取0个的最佳状态是0for (int i = 0; i < n; i++) {//从0~n-1枚举位数for (int j = 0; j < k; j++) {//取j个转移到取j+1个for (int mask = 0; mask < 4; mask++) {//4a[l],b[l]个状态int s1 = (mask & 1 ? -1 : 1);//a[i]的状态int s2 = (mask & 2 ? -1 : 1);//b[i]的状态dp[i][j + 1][mask] = max(dp[i][j + 1][mask], dp[i][j][4] + s1 * a[i] + s2 * b[i]);
//第i位取j+1个是从第i位取j个的最佳状态转移过去的}}for (int j = 0; j <= k; j++) {//当前取j个for (int mask = 0; mask < 4; mask++) {//枚举b[r],a[r]的状态int s1 = (mask & 1 ? -1 : 1);//b[r]int s2 = (mask & 2 ? -1 : 1);//a[r]dp[i][j][4] = max(dp[i][j][4], dp[i][j][mask] - s2 * a[i] - s1 * b[i]);
//因为mask的状态只有a[l],b[l]是不完整的最大值,我们从不完整的加上b[r],a[r]就成了完整的状态就
//是转移到dp[i][j][4]中表示前i为取j个的最大值if (j != k) dp[i + 1][j + 1][mask] = dp[i][j][mask];
//如果取的个数不到k个的话,不完整的状态就可以继续往下传递}dp[i + 1][j][4] = max(dp[i + 1][j][4], dp[i][j][4]);
//最后前i个取j个的最大值转移到前i+1个取j个的最大值}}cout << dp[n][k][4] << '\n';
//输出前n个取k个的最大值}
}
相关文章:

E. Maximum Monogonosity
You are given an array aa of length nn and an array bb of length nn. The cost of a segment [l,r][l,r], 1≤l≤r≤n1≤l≤r≤n, is defined as |bl−ar||br−al||bl−ar||br−al|. Recall that two segments [l1,r1][l1,r1], 1≤l1≤r1≤n1≤l1≤r1≤n, and [l2,r2][l2,…...

已解决Excel file format cannot be determined, you must specify an engine manually
问题 我使用以下语句时出现错误 data pd.read_excel(temp_inputc.csv, headerNone)出现错误: Excel file format cannot be determined, you must specify an engine manually有很多人说添加engine,但接下来会出现这个错误: File is not…...

Centos yum命令大全
1.使用YUM查找软件包 $ yum search python 2.列出所有可安装的软件包 $ yum list | grep python 3.列出所有可更新的软件包 $ yum list updates 4.列出所有已安装的软件包 $ yum list installed | grep python...

内网横向移动—ARP攻击图片捕捉数据劫持DNS劫持
内网横向移动—ARP攻击&图片捕捉&数据劫持&DNS劫持 1. ARP1.1. APR介绍1.1.1. ARP工作原理1.1.2. APR欺骗工作原理 1.2. 环境准备1.3. 适用场景 2. ARP断网攻击演示2.1. 使用kali进行演示2.1.1. nmap判断存活2.1.2. 安装工具2.1.3. 攻击Windows 10虚拟机2.1.3.1. 查…...

react之Hooks的介绍、useState与useEffect副作用的使用
react之Hooks的介绍、useState与useEffect副作用的使用 一、Hooks的基本介绍二、useState的使用2.1 简单使用2.2 数组结构简化2.3 状态的读取和修改2.3 组件的更新过程 三、useEffect的使用3.1 副作用介绍3.2 基本使用3.3 依赖3.4 不要对依赖项撒谎3.5 依赖项可以是空数组3.6 清…...
django——创建 Django 项目和 APP
2.创建 Django 项目和 APP 命令: 创建Django项目 django-admin startproject name 创建子应用 python manager.py startapp name 2.1 创建工程 在使用Flask框架时,项目工程目录的组织与创建是需要我们自己手动创建完成的。 在django中,…...

== 和 equals 的对比 [面试题]
和 equals 的对比[面试题] 文章目录 和 equals 的对比[面试题]1. 和 equals 简介2. Object 类中 equals() 源码3. String 类中 equals() 源码4. Integer 类中 equals() 源码5. 如何重写 equals 方法 1. 和 equals 简介 是一个比较运算符 :既可以判断基本数据类型…...
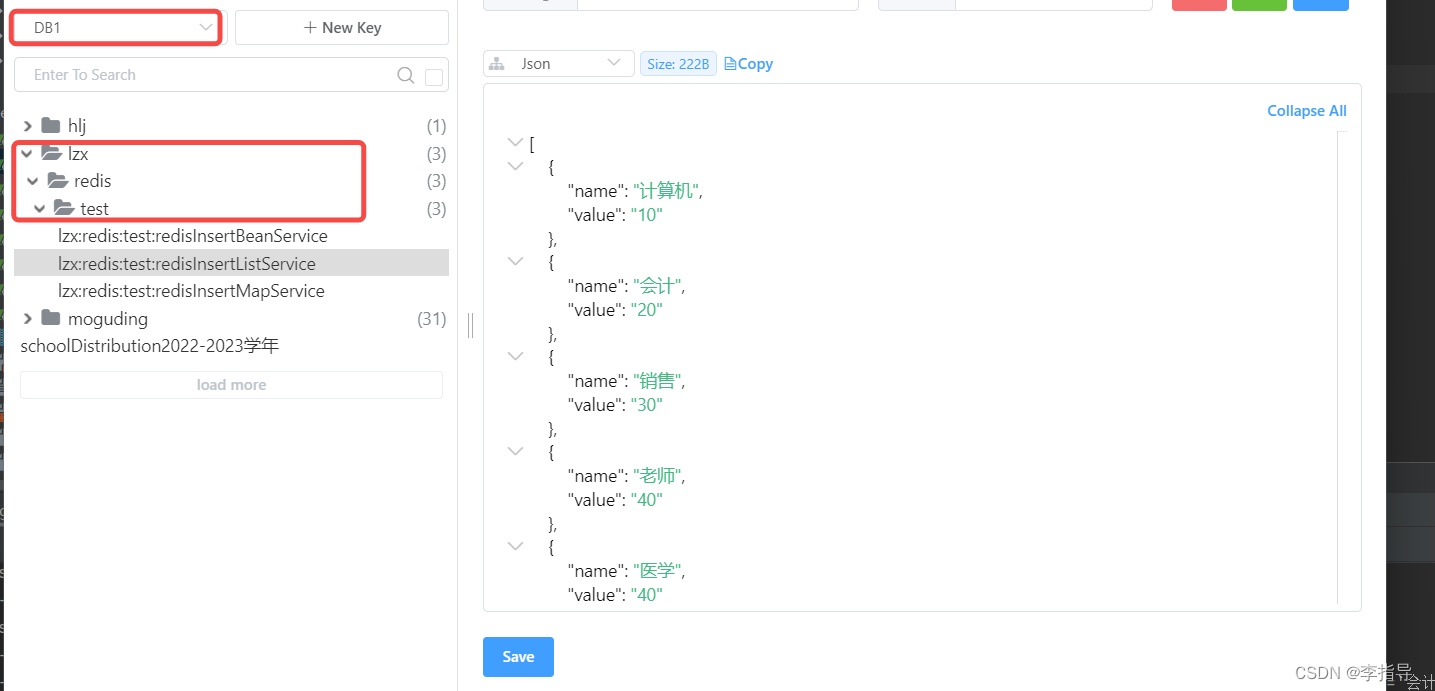
SpringBoot集成Redis及Redis使用方法
目录 应用背景 Redis简介 更新问题 一:环境配置 1.1: 在pom.xml文件中添加依赖 1.2:配置SpringBoot核心配置文件application.properties 二:在Config文件夹中创建RedisConfig配置文件类 2.1:RedisTemplate中的几个角色&am…...

Redis可以用作数据库吗?它的适用场景是什么?
是的,Redis可以用作数据库。虽然Redis通常被认为是一个内存数据库(in-memory database),但它也可以通过持久化机制将数据保存在磁盘上,以便在重启后恢复数据。 Redis的适用场景包括但不限于以下几个方面: …...

@Param详解
文章目录 背景什么是ParamParam的使用方法使用方法:遇到的问题及因Param解决了什么问题使用与不使用对比 Param是如何进行映射的总结 背景 最近在开发过程中,在写mapper接口是在参数前加了Param注解,但是在运行的时候就会报错,说…...

自定义分页工具类
前言 在日常的开发工作中,会遇到很多不确定的需求场景,无法使用第三方提供的分页组件来实现,那么如何自己实现一个简单的分页工具类呢? 工具类 第一版本: Setter Getter public class PageTool<T> {/*** 当前…...

文本数据保存
文本数据保存 工具目的代码运行结果 工具 pycharm 目的 网址:https://ljgk.envsc.cn/ 需求:获取到地址(address),公司名字(ps_name),创建的时间(create_time)ÿ…...
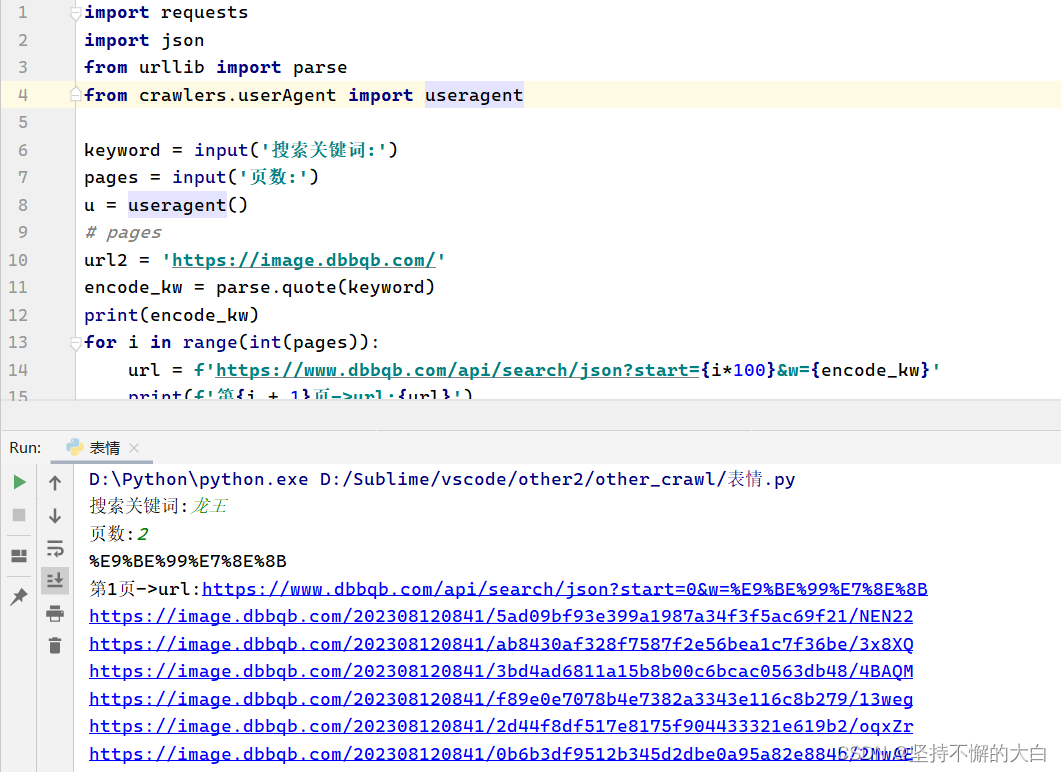
Python爬虫:抓取表情包的下载链接
Python爬虫:抓取表情包的下载链接 1. 前言2. 具体实现3. 实现代码 1. 前言 最近发现了一个提供表情包的网址,觉得上面的内容不错,于是就考虑用Python爬虫获取上面表情包的下载链接。整体而言,实现这个挺简单的,就是找到提供表情包…...
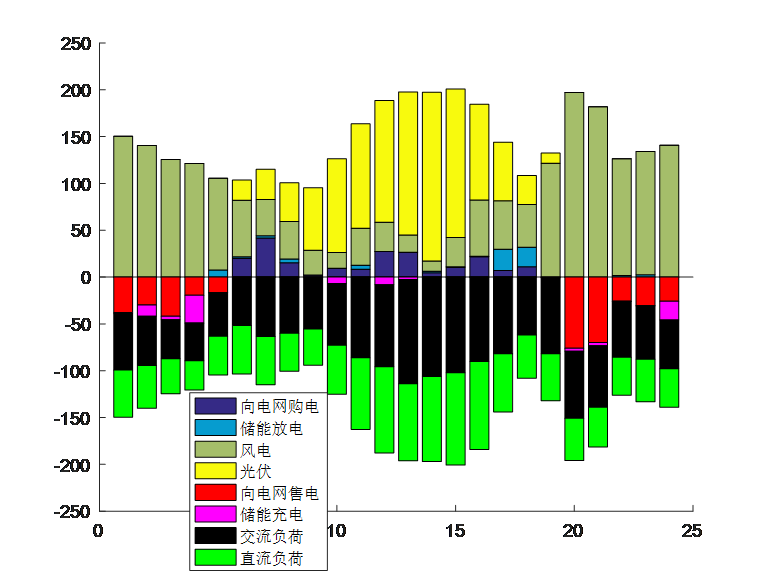
(文章复现)基于灰狼算法(GWO)的交直流混合微网经济调度matlab代码
参考文献: [1]高瑜,黄森,陈刘鑫等.基于改进灰狼算法的并网交流微电网经济优化调度[J].科学技术与工程, 2020,20(28):11605-11611. [2]邓长征,冯朕,邱立等.基于混沌灰狼算法的交直流混合微网经济调度[J].电测与仪表, 2020, 57(04):99-107. 这两篇文章不管是从模型、…...

【Kubernetes】Kubernetes的调度
K8S调度 一、Kubernetes 调度1. Pod 调度介绍2. Pod 启动创建过程3. Kubernetes 的调度过程3.1 调度需要考虑的问题3.2 具体调度过程 二、影响kubernetes调度的因素1. nodeName2. nodeSelector3. 亲和性3.1 三种亲和性的区别3.2 键值运算关系3.3 节点亲和性3.4 Pod 亲和性3.5 P…...

题目:2511.最多可以摧毁的敌人城堡数量
题目来源: leetcode题目,网址:2511. 最多可以摧毁的敌人城堡数目 - 力扣(LeetCode) 解题思路: 顺序遍历数组,记录上一个我军城堡和没有城堡的位置。当碰到空位置时,若上一次更新的…...

22 | 书籍推荐数据分析
import numpy as np import pandas as pd import seaborn as sns import matplotlib.pyplot as plt from sklearn.cluster import KMeans from sklearn import neighbors from sklearn.model_selection import train_test_split from sklearn.preprocessing import...

vscode extension 怎么区分dev prod
开发模式注入环境变量 使用vsode 提供的api...

Java学习手册——第一篇Java简介
今后Java学习手册就来给大家梳理JavaSE的基础知识啦, 除了这个专栏我们还有其他专栏:前端、安全、后端等。 希望大家可以在这里一起讨论学习哟~ Java学习手册——第一篇Java简介 1. Java基础知识2. Java能干嘛3. Java基础环境搭建 1. Java基础知识 出生…...
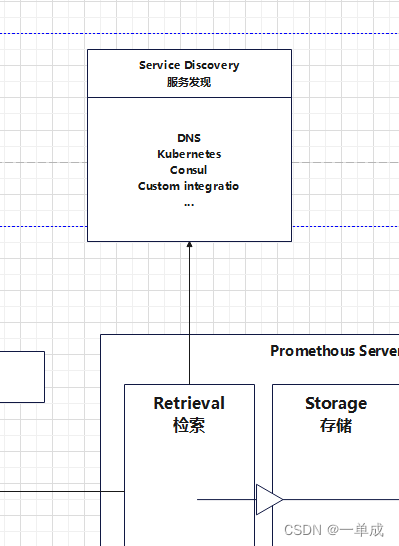
Prometheus流程图(自绘)-核心组件-流程详解
阿丹手绘流程图:图片可能有点小查看的时候放大看看哈! prometheus核心组件 prometheus server Prometheus Server是Prometheus组件中的核心部分,负责实现对监控数据的获取,存储以及查询。Prometheus Server可以通过静态配置管理…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...
