第三章,矩阵,07-用初等变换求逆矩阵、矩阵的LU分解
第三章,矩阵,07-用初等变换求逆矩阵、矩阵的LU分解
- 一个基本的方法
- 求 A − 1 B A^{-1}B A−1B
- LU分解
- 例1,求矩阵A的LU分解:
- 例12,LU分解解线性方程组:
玩转线性代数(19)初等矩阵与初等变换的相关应用的笔记,例见原文
一个基本的方法
已知: A r ∼ F A^r \sim F Ar∼F,求可逆阵 P P P,使 P A = F PA = F PA=F ( F F F为 A A A的行最简形)
方法:利用初等行变换,将矩阵A左边所乘初等矩阵相乘,从而得到可逆矩阵P.
步骤:
(1)对矩阵A进行l次初等行变换至行最简形:
A r ∼ F A^r \sim F Ar∼F,即 P l . . . P 2 P 1 A r = F P_l...P_2P_1A^r = F Pl...P2P1Ar=F
(2)求 P = P l . . . P 2 P 1 P=P_l...P_2P_1 P=Pl...P2P1
将 ( A , E ) (A, E) (A,E)看成分块矩阵,后面的E为记录器,对分块矩阵 ( A , E ) (A, E) (A,E)进行初等行变换:
( A , E ) → P l . . . P 2 P 1 ( A , E ) → ( P l . . . P 2 P 1 A , P l . . . P 2 P 1 ) → ( P A , P ) → ( F , P ) (A, E) \rightarrow P_l...P_2P_1(A, E) \rightarrow (P_l...P_2P_1A, P_l...P_2P_1) \rightarrow (PA, P) \rightarrow (F, P) (A,E)→Pl...P2P1(A,E)→(Pl...P2P1A,Pl...P2P1)→(PA,P)→(F,P)
即当A化为F后E化为P。
那么若A可逆, A − 1 A = E A^{-1}A = E A−1A=E,即将A化为单位阵,右边的E就化为 A − 1 A^{-1} A−1
求 A − 1 B A^{-1}B A−1B
即将上面的“记录器”E换为B,将A化为E的一系列行变换操作(等效于左乘 A − 1 A^{-1} A−1)全部作用到B上
A − 1 ( A , B ) = ( E , A − 1 B ) A^{-1}(A, B)=(E,A^{-1}B) A−1(A,B)=(E,A−1B)
LU分解
假设A是m*n矩阵并且可以化简为行阶梯形而不必经过行对换或数乘,则A可以分解成如下的形式:
A = ( 1 0 0 0 ∗ 1 0 0 ∗ ∗ 1 0 ∗ ∗ ∗ 1 ) ( ■ ∗ ∗ ∗ ∗ 0 ■ ∗ ∗ ∗ 0 0 0 ■ ∗ 0 0 0 0 0 ) = L U A= \begin{pmatrix} 1 & 0 & 0 & 0 \\* & 1 & 0 & 0 \\* & * & 1 & 0\\* & * & * & 1 \end{pmatrix} \begin{pmatrix} \blacksquare & * & * & * & * \\0 & \blacksquare & * & * & * \\0 & 0 & 0 & \blacksquare & *\\0 & 0 & 0 & 0 & 0 \end{pmatrix} =LU A= 1∗∗∗01∗∗001∗0001 ■000∗■00∗∗00∗∗■0∗∗∗0 =LU
L是单位下三角矩阵,主对角线元素全是1,它其实是一系列 E ( i j ( k ) ) E(ij(k)) E(ij(k))类型初等矩阵的乘积,L可逆;U是A的一个等价的行阶梯形矩阵。
例1,求矩阵A的LU分解:
令
A = ( 2 4 2 1 5 2 4 − 1 9 ) A= \begin{pmatrix} 2 & 4 & 2 \\ 1 & 5 & 2 \\ 4 & -1 & 9 \end{pmatrix} A= 21445−1229
则
( A , E ) = ( 2 4 2 1 0 0 1 5 2 0 1 0 4 − 1 9 0 0 1 ) ∼ ( 2 4 2 1 0 0 0 3 1 − 1 2 1 0 0 − 9 5 − 2 0 1 ) ∼ ( 2 4 2 1 0 0 0 3 1 − 1 2 1 0 0 0 8 − 7 2 3 1 ) = ( U , p ) (A,E)=\begin{pmatrix} 2 & 4 & 2 & 1 & 0 & 0 \\ 1 & 5 & 2 & 0 & 1 & 0 \\ 4 & -1 & 9 & 0 & 0 & 1 \end{pmatrix} \sim \begin{pmatrix} 2 & 4 & 2 & 1 & 0 & 0 \\ 0 & 3 & 1 & -\frac{1}{2} & 1 & 0 \\ 0 & -9 & 5 & -2 & 0 & 1 \end{pmatrix}\sim \begin{pmatrix} 2 & 4 & 2 & 1 & 0 & 0 \\ 0 & 3 & 1 & -\frac{1}{2} & 1 & 0 \\ 0 & 0 & 8 & -\frac{7}{2} & 3 & 1 \end{pmatrix} =(U, p) (A,E)= 21445−1229100010001 ∼ 20043−92151−21−2010001 ∼ 2004302181−21−27013001 =(U,p)
故 U = P A ⇒ A = P − 1 U U=PA \Rightarrow A=P^{-1}U U=PA⇒A=P−1U,有
A = ( 2 4 2 1 5 2 4 − 1 9 ) = ( 1 0 0 1 2 1 0 2 − 3 1 ) ( 2 4 2 0 3 1 0 0 8 ) = L U A= \begin{pmatrix} 2 & 4 & 2 \\ 1 & 5 & 2 \\ 4 & -1 & 9 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0\\ \frac{1}{2} & 1 & 0\\ 2 & -3 & 1 \end{pmatrix} \begin{pmatrix} 2 & 4 & 2\\ 0 & 3 & 1\\ 0 & 0 & 8 \end{pmatrix}=LU A= 21445−1229 = 121201−3001 200430218 =LU
例12,LU分解解线性方程组:
将系数矩阵进行LU分解,然后分两步解出方程

在具体求解时要使用数学软件来求,计算机解线性方程组时就采用LU分解.手动进行LU分解当然是比较麻烦的.
相关文章:

第三章,矩阵,07-用初等变换求逆矩阵、矩阵的LU分解
第三章,矩阵,07-用初等变换求逆矩阵、矩阵的LU分解 一个基本的方法求 A − 1 B A^{-1}B A−1BLU分解例1,求矩阵A的LU分解:例12,LU分解解线性方程组: 玩转线性代数(19)初等矩阵与初等变换的相关应用的笔记&a…...
STM32F429IGT6使用CubeMX配置SPI通信(W25Q256芯片)
1、硬件电路 需要系统性的看一下W25Q256芯片手册 2、设置RCC,选择高速外部时钟HSE,时钟设置为180MHz 3、配置SPI 4、生成工程配置 5、相关代码 #define sFLASH_ID 0XEF4019 // W25Q256#define SPI_FLASH_PageSize 256 #define SPI_FLASH_PerWritePageSize 256#def…...

C++11异步与通信之 packaged_task
概念简介 packaged_task 用于包装可调用目标(Callable)为一个对象,如lambda,普通函数,小括号重载等,用于异步调用。 其返回值或所抛异常被存储于能通过 std::future 对象访问的共享状态中,和promise类似。 将函数的调用与函数返…...
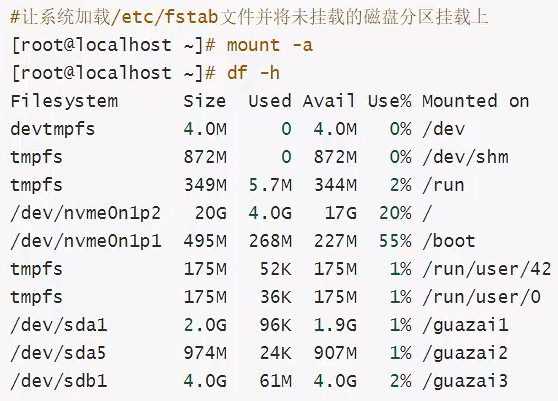
磁盘的管理
一、磁盘的分区 查看磁盘 lsblk fdisk -l 2、分区 没有e扩展,则都是主分区,已经有三个主分区了,剩下的全设置为扩展 查看分区结果: 二、格式化 三、挂载...

数据结构:完全二叉树的性质
完全二叉树的性质: 具有 n n n个结点的完全二叉树的深度为 [ l o g 2 n ] 1 ( [ x ] 表示不大于 x 的最大整数 ) [log_2n]1([x]表示不大于x的最大整数) [log2n]1([x]表示不大于x的最大整数) 对于任意一个结点 ( 1 < i < n ) &…...
【数据结构】‘双向链表’冲冲冲
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...
Linux 编译CEF源码详细记录
Linux CEF(Chromium Embedded Framework)源码下载编译 背景 由于CEF默认的二进制分发包不支持音视频播放,需要自行编译源码,将ffmpeg开关打开才能支持。这里介绍的是Linux平台下的CEF源码下载编译过程。 Windows平台参考&#…...

LeetCode 2810. Faulty Keyboard【模拟,双端队列,字符串】简单
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
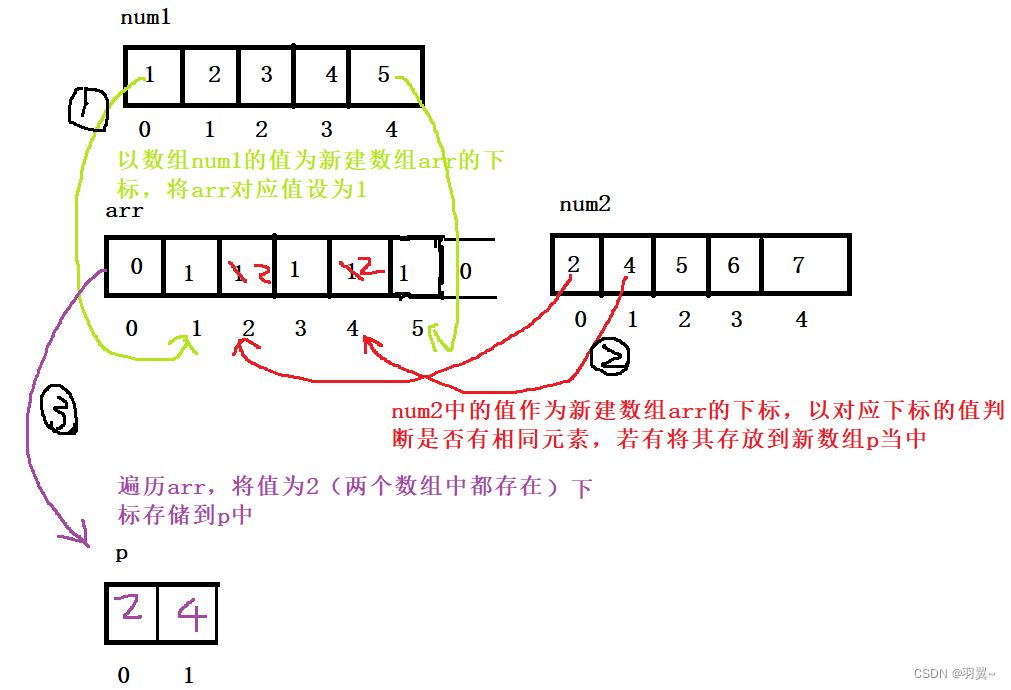
两个数组的交集-C语言/Java
描述 给定两个数组 nums1 和 nums2 ,返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序。(1 < nums1.length, nums2.length < 1000,0 < nums1[i], nums2[i] < 1000) 示例1 输入…...

Arduino+esp32学习笔记
学习目标: 使用Arduino配置好蓝牙或者wifi模块 学习使用python配置好蓝牙或者wifi模块 学习内容(笔记): 一、 Arduino语法基础 Arduino语法是基于C的语法,C又是c基础上增加了面向对象思想等进阶语言。那就只记录没见过的。 单多…...

计算机网络-专业术语
计算机网络-专业术语 实体 实体:任何可发送或接收信息的硬件或软件进程 对等实体:收发双方相同层次中的实体 协议 控制两个对等实体进行逻辑通信的规则的集合 协议三要素 语法 定义所交换的信息的格式 是用户数据与控制信息的结构和格式 语义 定义收发双方所需要完成的操作…...

E. Maximum Monogonosity
You are given an array aa of length nn and an array bb of length nn. The cost of a segment [l,r][l,r], 1≤l≤r≤n1≤l≤r≤n, is defined as |bl−ar||br−al||bl−ar||br−al|. Recall that two segments [l1,r1][l1,r1], 1≤l1≤r1≤n1≤l1≤r1≤n, and [l2,r2][l2,…...

已解决Excel file format cannot be determined, you must specify an engine manually
问题 我使用以下语句时出现错误 data pd.read_excel(temp_inputc.csv, headerNone)出现错误: Excel file format cannot be determined, you must specify an engine manually有很多人说添加engine,但接下来会出现这个错误: File is not…...

Centos yum命令大全
1.使用YUM查找软件包 $ yum search python 2.列出所有可安装的软件包 $ yum list | grep python 3.列出所有可更新的软件包 $ yum list updates 4.列出所有已安装的软件包 $ yum list installed | grep python...

内网横向移动—ARP攻击图片捕捉数据劫持DNS劫持
内网横向移动—ARP攻击&图片捕捉&数据劫持&DNS劫持 1. ARP1.1. APR介绍1.1.1. ARP工作原理1.1.2. APR欺骗工作原理 1.2. 环境准备1.3. 适用场景 2. ARP断网攻击演示2.1. 使用kali进行演示2.1.1. nmap判断存活2.1.2. 安装工具2.1.3. 攻击Windows 10虚拟机2.1.3.1. 查…...

react之Hooks的介绍、useState与useEffect副作用的使用
react之Hooks的介绍、useState与useEffect副作用的使用 一、Hooks的基本介绍二、useState的使用2.1 简单使用2.2 数组结构简化2.3 状态的读取和修改2.3 组件的更新过程 三、useEffect的使用3.1 副作用介绍3.2 基本使用3.3 依赖3.4 不要对依赖项撒谎3.5 依赖项可以是空数组3.6 清…...
django——创建 Django 项目和 APP
2.创建 Django 项目和 APP 命令: 创建Django项目 django-admin startproject name 创建子应用 python manager.py startapp name 2.1 创建工程 在使用Flask框架时,项目工程目录的组织与创建是需要我们自己手动创建完成的。 在django中,…...

== 和 equals 的对比 [面试题]
和 equals 的对比[面试题] 文章目录 和 equals 的对比[面试题]1. 和 equals 简介2. Object 类中 equals() 源码3. String 类中 equals() 源码4. Integer 类中 equals() 源码5. 如何重写 equals 方法 1. 和 equals 简介 是一个比较运算符 :既可以判断基本数据类型…...
SpringBoot集成Redis及Redis使用方法
目录 应用背景 Redis简介 更新问题 一:环境配置 1.1: 在pom.xml文件中添加依赖 1.2:配置SpringBoot核心配置文件application.properties 二:在Config文件夹中创建RedisConfig配置文件类 2.1:RedisTemplate中的几个角色&am…...

Redis可以用作数据库吗?它的适用场景是什么?
是的,Redis可以用作数据库。虽然Redis通常被认为是一个内存数据库(in-memory database),但它也可以通过持久化机制将数据保存在磁盘上,以便在重启后恢复数据。 Redis的适用场景包括但不限于以下几个方面: …...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
