工博士与纷享销客达成战略合作,开启人工智能领域合作新篇章
近日,工博士与纷享销客在上海正式签署了战略合作协议,正式拉开了双方在人工智能与数字营销领域的合作序幕。这次合作将为双方带来更多机遇和发展空间,并为全球人工智能领域的客户提供更高效、智能的CRM解决方案。

< 双方项目人员合影 >
未来,工博士和纷享销客将继续加强合作,共同探索人工智能领域的营销创新,为客户创造更大价值。双方将充分发挥各自的优势,通过深度合作和共同努力,推动人工智能+数字营销的发展,为行业的升级和转型注入新的动力。


关于工博士
工博士是一家位于上海的科技公司,专注于机器人、智能装备、自动化设备及配件等产品。工博士已在行业内树立了良好品牌形象和竞争优势。目标是让智造更简单,成为智能服务提供者,推动智能产业升级。业务覆盖智能装备、产业互联网、工业自动化和装备出口。以平台化为支撑,整合资源,提高自动化设备供给效率,降低成本,推动中国智能装备行业技术进步。
相关文章:

工博士与纷享销客达成战略合作,开启人工智能领域合作新篇章
近日,工博士与纷享销客在上海正式签署了战略合作协议,正式拉开了双方在人工智能与数字营销领域的合作序幕。这次合作将为双方带来更多机遇和发展空间,并为全球人工智能领域的客户提供更高效、智能的CRM解决方案。 < 双方项目人员合影 >…...

拆解与重构:慕云游首页组件化设计
目录 前言1 项目准备1.1 创建项目目录1.2 搭建项目开发环境 2 项目组件化2.1 在当前环境启动原有项目2.2 顶部组件2.3 幻灯片组件2.4 机酒自由行组件2.5 拆分余下的css文件 3 项目完善3.1 幻灯片组件3.1.1 结构和样式3.1.2 功能实现3.1.3 使用Ajax获取数据3.1.4 加载中组件 3.2…...

刷了3个月的华为OD算法题,刷出感觉了,如洁柔般丝滑,文末送《漫画算法2:小灰的算法进阶》
目录 一、考研二战,入职华为,反向调剂电子科大深圳下面分享一道2023 B卷 朋友抽中题 简易内存池:二、题目描述三、输入描述四、输出描述样例:输出样例: 五、解题思路六、Java算法源码七、效果展示1、输入2、输出3、说明…...

ip转换器哪个好用 ip地址切换器有哪些
在互联网时代,IP转换器成为了实现高效工作的常见工具。而如今,市面上涌现出了众多的IP转换器软件,使得用户在选择时感到困惑。本文将介绍一种深度IP转换器软件,探讨其特点和优势,以及与其他软件相比的差异,…...
【python】爬取豆瓣电影Top250(附源码)
前言 在网络爬虫的开发过程中,经常会遇到需要处理一些反爬机制的情况。其中之一就是网站对于频繁访问的限制,即IP封禁。为了绕过这种限制,我们可以使用代理IP来动态改变请求的来源IP地址。在本篇博客中,将介绍如何使用代理IP的技术…...

35岁职业危机?不存在!体能断崖?不担心
概述 90年,硕士毕业,干了快8年的Java开发工作。现年33岁,再过2年就要35岁。 工作这些年,断断续续也看过不少35岁找不到工作,转行,降薪入职的传闻、案例。 35岁,甚至30岁之后,体能…...

C语言——指针进阶
本章重点 字符指针数组指针指针数组数组传参和指针传参函数指针函数指针数组指向函数指针数组的指针回调函数指针和数组面试题的解析 1. 字符指针 在指针的类型中我们知道有一种指针类型为字符指针 char* int main() { char ch w; char *pc &ch; *pc w; return 0; }…...

heap pwn 入门大全 - 1:glibc heap机制与源码阅读(上)
本文为笔者学习heap pwn时,学习阅读glibc ptmalloc2源码时的笔记,与各位分享。可能存在思维跳跃或错误之处,敬请见谅,欢迎在评论中指出。本文也借用了部分外网和其他前辈的素材图片,向各位表示诚挚的感谢!如…...
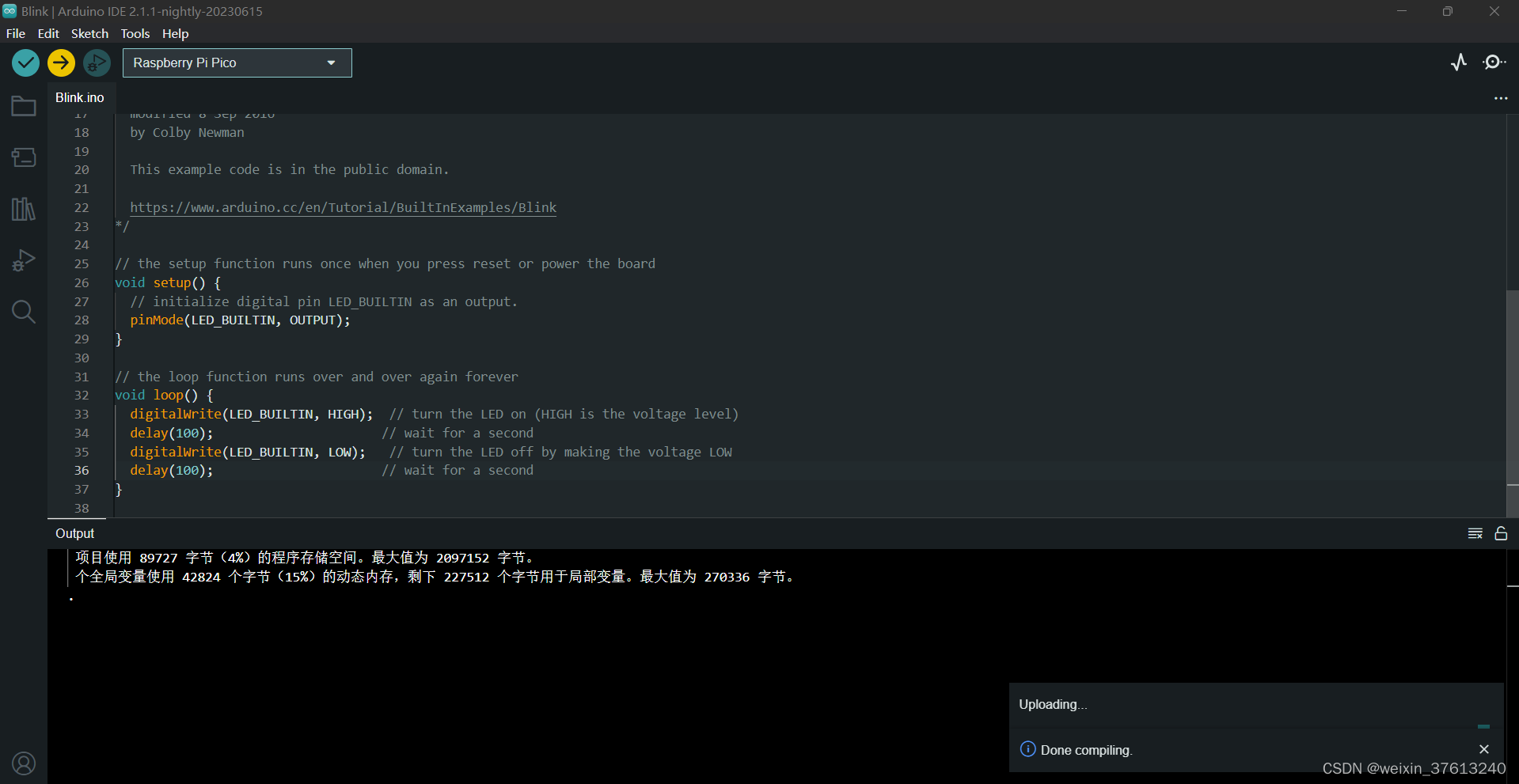
树莓派RP2040 用Arduino IDE安装和编译
目录 1 Arduino IDE 1.1 IDE下载 1.2 安装 arduino mbed os rp2040 boards 2 编程-烧录固件 2.1 打开点灯示例程序 2.2 选择Raspberry Pi Pico开发板 2.3 编译程序 2.4 烧录程序 2.4.1 Raspberry Pi Pico开发板首次烧录提示失败 2.4.2 解决首次下载失败问题 2.4.2.1…...

云安全攻防(八)之 Docker Remote API 未授权访问逃逸
Docker Remote API 未授权访问逃逸 基础知识 Docker Remote API 是一个取代远程命令行界面(rcli)的REST API,其默认绑定2375端口,如管理员对其配置不当可导致未授权访问漏洞。攻击者利用 docker client 或者 http 直接请求就可以…...

2023-08-13 LeetCode每日一题(合并两个有序数组)
2023-08-13每日一题 一、题目编号 88. 合并两个有序数组二、题目链接 点击跳转到题目位置 三、题目描述 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 …...

nbcio-boot升级springboot、mybatis-plus和JSQLParser后的LocalDateTime日期json问题
升级后,运行显示项目的时候出现下面错误 2023-08-12 10:57:39.174 [http-nio-8080-exec-3] [1;31mERROR[0;39m [36morg.jeecg.common.aspect.DictAspect:104[0;39m - json解析失败Java 8 date/time type java.time.LocalDateTime not supported by default: add Mo…...
「C/C++」C/C++搭建程序框架
✨博客主页何曾参静谧的博客📌文章专栏「C/C」C/C程序设计📚全部专栏「UG/NX」NX二次开发「UG/NX」BlockUI集合「VS」Visual Studio「QT」QT5程序设计「C/C」C/C程序设计「Win」Windows程序设计「DSA」数据结构与算法「File」数据文件格式 目录 1. 分离职…...
Android 内存泄漏
名词解释 内存泄漏:即memory leak。是指内存空间使用完毕后无法被释放的现象,虽然Java有垃圾回收机制(GC),但是对于还保持着引用, 该内存不能再被分配使用,逻辑上却已经不会再用到的对象,垃圾回…...

Android上的基于协程的存储框架
在Android上,经常会需要持久化本地数据,比如我们需要缓存用户的配置信息、用户的数据、缓存数据、离线缓存数据等等。我们通常使用的工具为SharePreference、MMKV、DataStore、Room、文件等等。通过使用现有的存储框架,结合协程,我…...

虚拟现实与增强现实技术的商业应用
章节一:引言 随着科技的不断发展,虚拟现实(Virtual Reality,简称VR)与增强现实(Augmented Reality,简称AR)技术正日益成为商业领域中的重要创新力量。这两种技术为企业带来了前所未…...

每日后端面试5题 第六天
1. Java中有几种类型的流 字符流、字节流 输入流、输出流 节点流、处理流 2 .Spring支持的几种bean的作用域 五种: 1.singleton bean在每个ioc容器中只有一个实例 2.prototype 可以有多个实例 3-5在web环境中才生效 3.request 每次请求才创建bean 4.se…...

LeetCode150道面试经典题-- 两数之和(简单)
1.题目 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。 你可以按任意…...
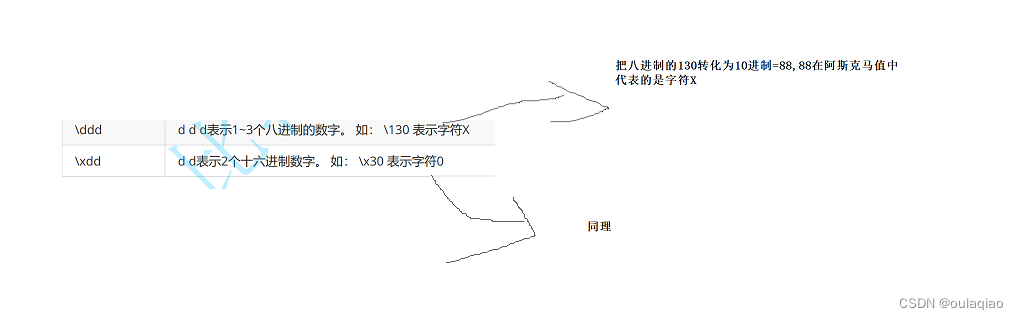
转义字符\
转移字符,就是通过字符,来转变原来字符的意思 常见的转义字符: 1、 2 注:" 的作用和他是类似的 3 4、 当打印\a时,电脑会出现一个警告,蜂鸣的声音 5、 阿斯克码表...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...

