第三章 图论 No.9有向图的强连通与半连通分量
文章目录
- 定义
- Tarjan求SCC
- 1174. 受欢迎的牛
- 367. 学校网络
- 1175. 最大半连通子图
- 368. 银河
定义
连通分量是无向图的概念,yxc说错了,不要被误导
强连通分量:在一个有向图中,对于分量中的任意两点u,v,一定能从u走到v,且能从v走到u。强连通分量是一些点的集合,若加入其他点,强连通分量中的任意两点就不能互相递达
半连通分量:在一个有向图中,对于分量中的任意两点u,v,一定存在从u走到v或者从v的路径
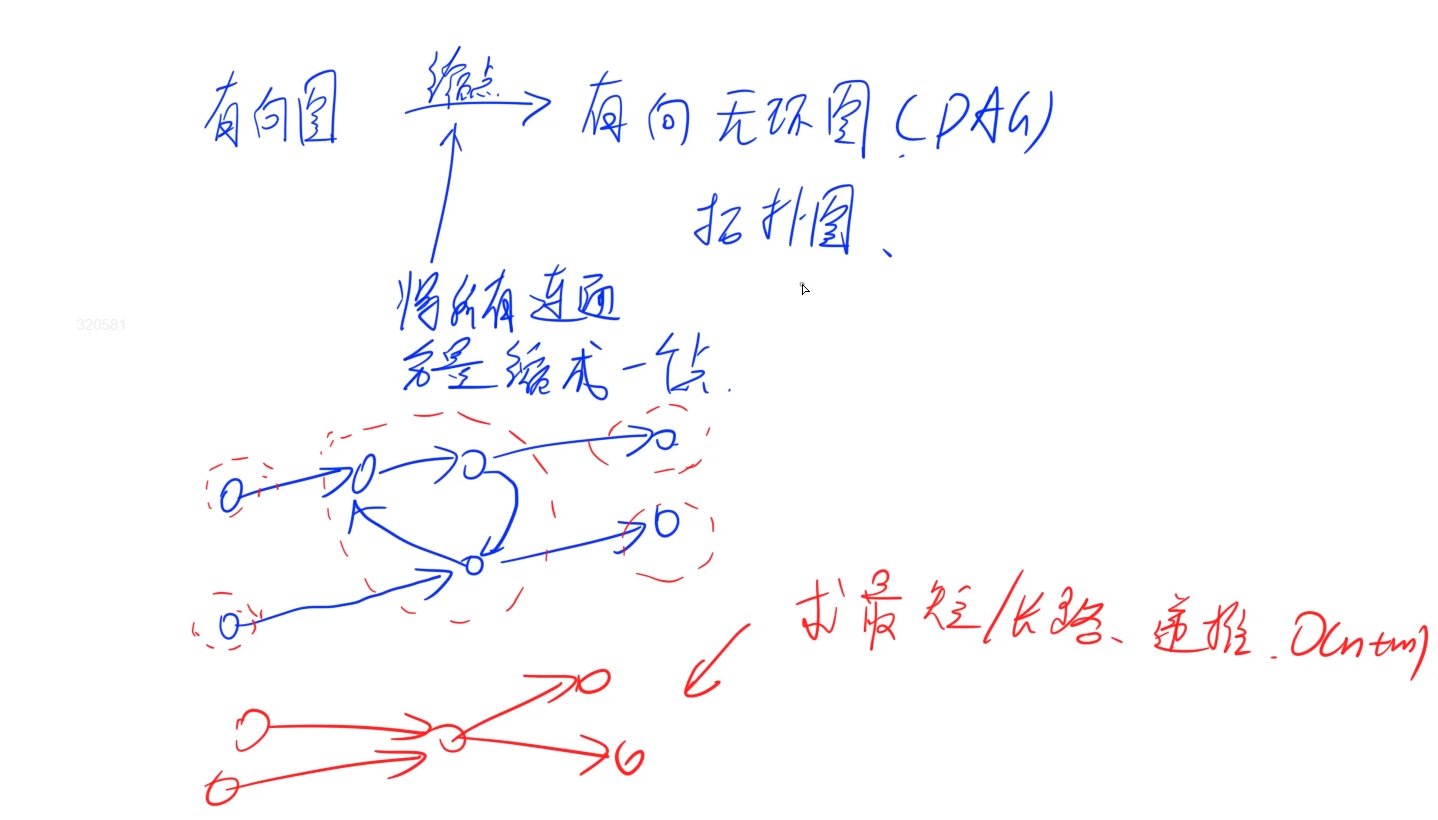
应用:通过缩点(将所有强连通分量缩成一个点)的方式,那么一个有向图就转换成了一个有向无环图DAG(拓扑图)
对于拓扑图,可以直接用bfs求最短路问题
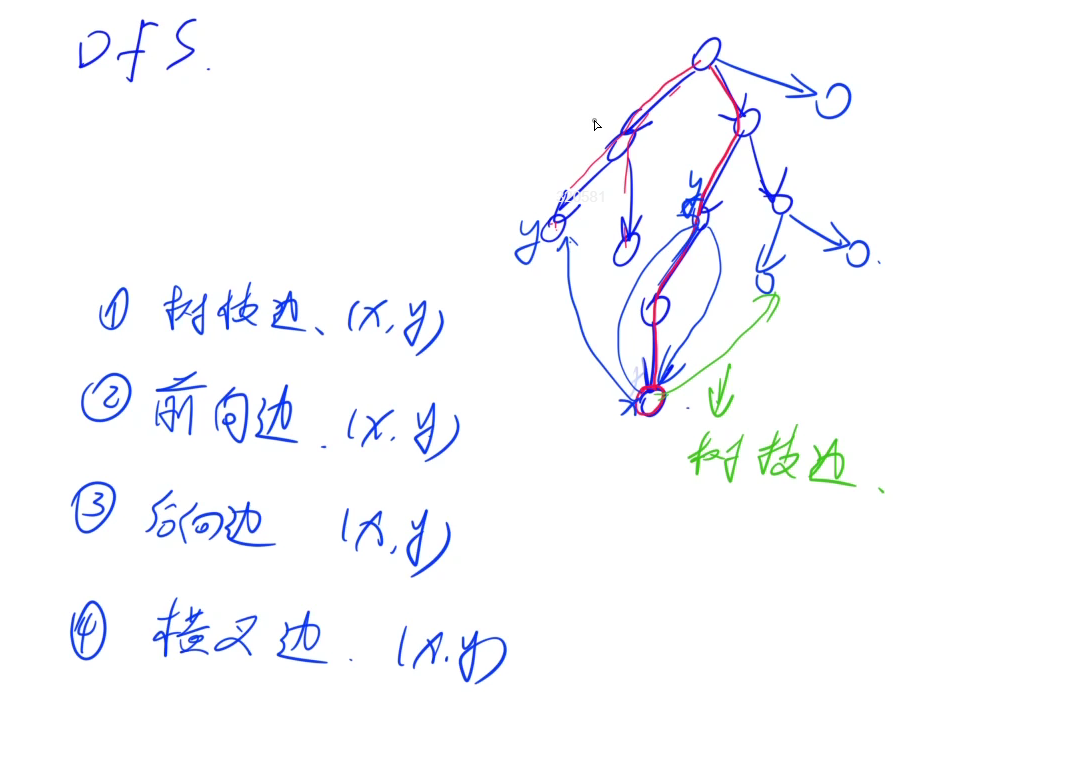
- 树枝边(x和y直接相连)
- 前向边(y是x的祖先节点)
- 后向边(前向边的反)
- 横叉边(指向已经遍历过的其他分支上的点)
树枝边是一种特殊的前向边
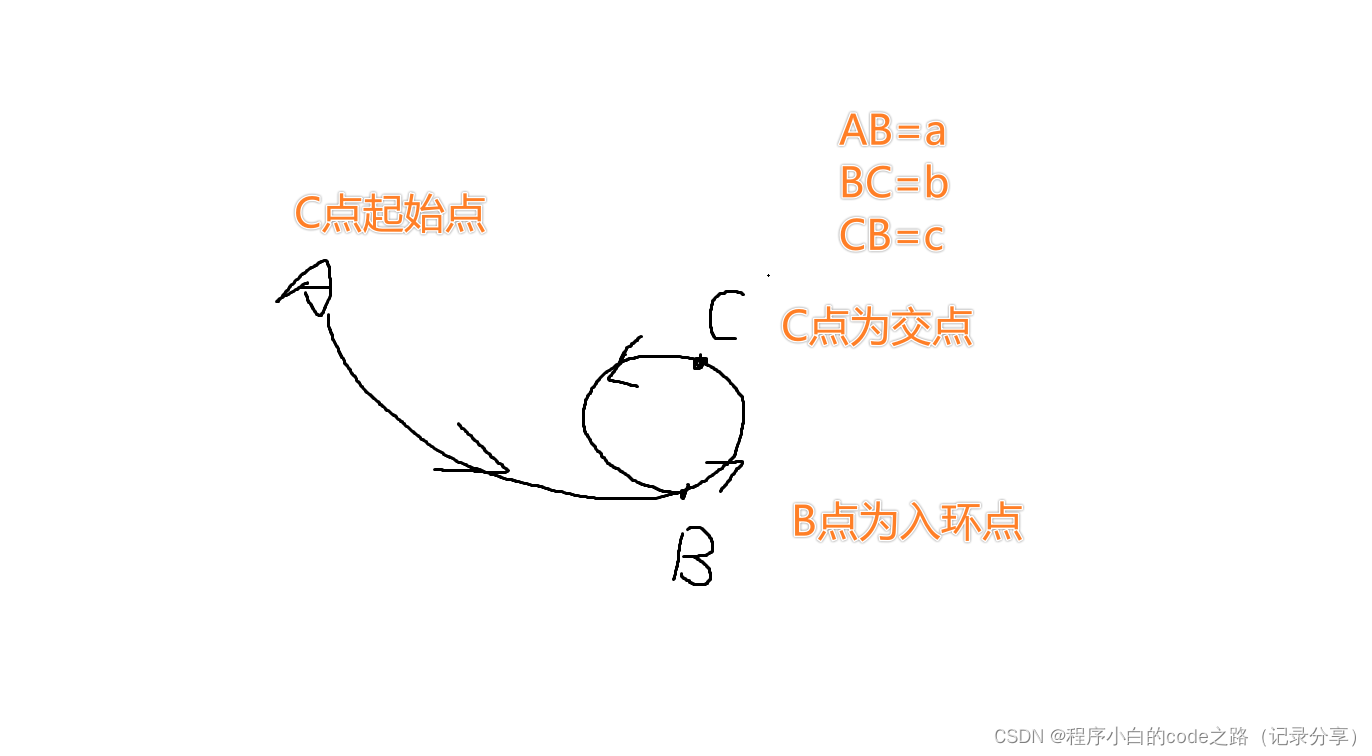
强连通分量简称scc,如何判断当前点是否在scc中?
- 存在一条后向边,指向祖先节点
- 先走横叉边,横叉边连接了后向边
无论如何,其一定能走到已经遍历过的祖先节点上
点可能存在自环,也是强连通分量(书上说自环不是强连通分量,但是为了算法的实现,将自环认为是强连通分量)
Tarjan求SCC
给定时间戳的概念,从小到大的时间为dfs的顺序
那树枝边的y一定比x大1,前向边的y一定大于等于x+1
后向边的y一定小于x,横叉边也是
对每个点定义两个时间戳:
dfs[u]表示遍历到u的时间
low[u]表示从u开始走,能遍历到的最小时间戳
若u是强连通分量的最高点,那么dfn[u] == low[u],即该点无法再往上走到其他点
板子中使用了两个栈,一个是系统函数栈,用来深搜。一个是自定义的栈,保存当前正在遍历的强连通分量中的所有点
板子 O ( n + m ) O(n + m) O(n+m):
void tarjan(int x)
{dfn[x] = low[x] = ++ tp;stk[ ++ tt] = x, st[x] = true;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!dfn[y]){tarjan(y);low[x] = min(low[x], low[y]);}else if (st[y]) low[x] = min(low[x], dfn[y]);}if (low[x] = dfn[x]){int y;++ cnt;do{y = stk[tt -- ], st[y] =false;id[y] = cnt;} while (y != x)}
}
缩点:遍历所有点,再遍历其所有邻点,若两点不在同一强连通分量中,将这两点之间添加一条边
强连通分量编号递减的顺序一定是拓扑序,求拓扑序一般使用bfs,除此之外还能使用dfs
遍历所有点,从入边为0的点开始,dfs其所有邻点,完成后将该点的编号加入序列中,序列的逆序就是拓扑序。因为每次进入序列的点一定无后继(或者后继节点已经进入序列的点)
不过,若图中存在多个入边为0的点,选择其一进行dfs即可,后续要在拓扑序开头加上这几个入边为0的点
1174. 受欢迎的牛
1174. 受欢迎的牛 - AcWing题库
反向建图,遍历所有点,用bfs判断当前点是否能递达其他所有点,时间复杂度为 O ( n 2 ) O(n^2) O(n2)
如果不反向建图,就要判断图中有几个出边为0的点,若有1个,那么这个点就是最受欢迎的,若有>1个,那么不存在最受欢迎的点,若有0个,说明图中一定存在环(强连通分量),环中的节点数量为受欢迎的点的数量
将所有的强连通分量(环)缩成一个点,此时图中出边为0的点的数量不可能为0
只要判断数量是否为1即可
若出边为的点的数量为1,说明该强连通分量中的所有点都是受欢迎的,统计环中节点的数量即可
#include <iostream>
#include <cstring>
using namespace std;const int N = 1e4 + 10, M = 5e4 + 10;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], tp, cnt;
int stk[N], tt; bool st[N];
int dout[N], id[N], sz[N]; // 每个强连通分量中的节点数量
int n, m;void add(int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}void tarjan(int x)
{stk[ ++ tt] = x, st[x] = true;dfn[x] = low[x] = ++ tp;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!dfn[y]){tarjan(y);low[x] = min(low[x], low[y]);}else if (st[y]) low[x] = min(low[x], dfn[y]);}if (dfn[x] == low[x]){int y;cnt ++ ;do {y = stk[tt -- ], st[y] = false;id[y] = cnt;sz[cnt] ++ ;} while (y != x);}
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);int x, y;for (int i = 0; i < m; ++ i ){scanf("%d%d", &x, &y);add(x, y);}for (int i = 1; i <= n; ++ i )if (!dfn[i]) tarjan(i);for (int x = 1; x <= n; ++ x ) for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];int a = id[x], b = id[y]; if (a != b) dout[a] ++ ;}int ans = 0, t = 0;for (int i = 1; i <= cnt; ++ i )if (!dout[i]){t ++ ;ans = sz[i];if (t > 1){ans = 0;break;}}printf("%d\n", ans);return 0;
}
debug到死的一道题:
首先tp要前置++,虽然tp是时间戳的概念,但是在数组中作为下标还对应着节点编号
最后检查dout数组中,循环从1到cnt,不是从1到n,也不是从1到cnt - 1,因为cnt不是后置++,而是++完再使用
else if (st[y]) low[x] = min(low[x], dfn[y]);写歪了,写成
else if (st[y]) low[x] = min(low[x], dfn[x]);
367. 学校网络
367. 学校网络 - AcWing题库
将所有强连通分量缩点后,图中入度为0的点为第一问的答案
第二问是:任何一个有向无环图,需要加几条边才能使之成为一个强连通分量
结论:假设有向无环图有P个入度为0的点,Q个出度为0的点,需要加max(P, Q)个点
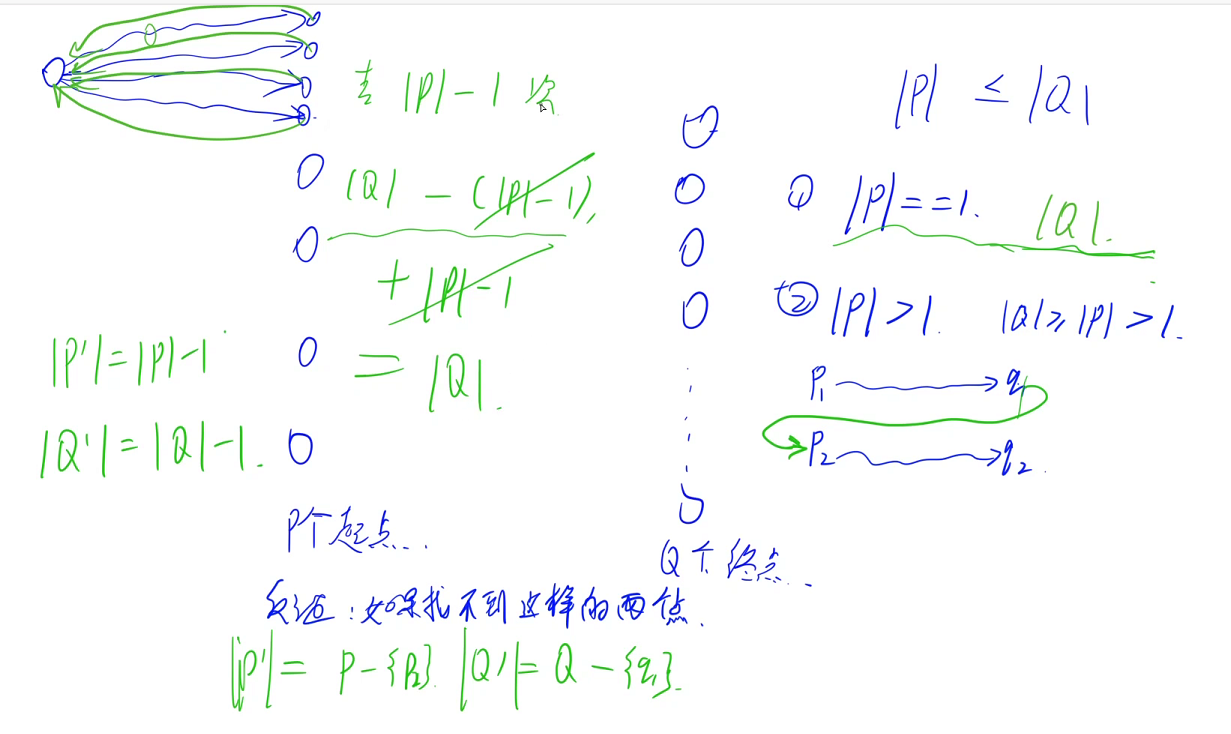
设起点的集合为P,终点的集合为Q
假设 ∣ P ∣ < = ∣ Q ∣ |P| <= |Q| ∣P∣<=∣Q∣,若 ∣ P ∣ > ∣ Q ∣ |P| > |Q| ∣P∣>∣Q∣,建个反图即可
考虑两种情况, ∣ P ∣ = 1 |P| = 1 ∣P∣=1,此时将所有的终点向起点连一条边,即 Q Q Q条边。此时从起点一定能走到所有点,从中间点一定能走到终点,而终点一定能走到起点,从而走完所有点。所以此时图中任意一点能走完图中所有点
∣ P ∣ > 1 |P| > 1 ∣P∣>1时,在终点与起点之间连一条边(尽可能与无法到达该终点的起点连线),直到起点的数量为1(每次连完边后,起点数量与终点数量都减一),此时的情况为 ∣ P ∣ = 1 |P|=1 ∣P∣=1的情况 ∣ Q ∣ − ( ∣ P ∣ − 1 ) |Q|-(|P|-1) ∣Q∣−(∣P∣−1)条边即可,由于已经连了 ∣ P ∣ − 1 |P|-1 ∣P∣−1条边,所以总共需要连的边数为 ∣ Q ∣ |Q| ∣Q∣
#include <iostream>
#include <cstring>
using namespace std;const int N = 110, M = N * N;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], tp, cnt;
int id[N], stk[N], tt;
bool st[N];
int din[N], dout[N];
int n, t;void add(int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}void tarjan(int x)
{st[x] = true, stk[ ++ tt] = x;dfn[x] = low[x] = ++ tp;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!dfn[y]){tarjan(y);low[x] = min(low[x], low[y]);}else if (st[y]) low[x] = min(low[x], dfn[y]);}if (dfn[x] == low[x]){int y;cnt ++ ;do {y = stk[tt -- ], st[y] = false;id[y] = cnt;} while (x != y);}
}int main()
{memset(h, -1, sizeof(h));scanf("%d", &n);int y;for (int x = 1; x <= n; ++ x )while (scanf("%d", &y), y)add(x, y);for (int i = 1; i <= n; ++ i )if (!dfn[i])tarjan(i);int u = 0;for (int x = 1; x <= n; ++ x)for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];int a = id[x], b = id[y];if (a != b) din[b] ++, dout[a] ++ ;}int in = 0, out = 0;for (int i = 1; i <= cnt; ++ i ){if (!din[i]) in ++ ;if (!dout[i]) out ++ ;}if (cnt == 1) printf("%d\n%d\n", in, 0);else printf("%d\n%d\n", in, max(in, out));return 0;
}
debug:dfs的次数与缩点后入度为0的点的数量不一定相同
缩点后的图中可能存在入度和出度都为0的点,所以判断要用两个if
最后要注意,缩点后的图只有一个连通分量时,需要特判输出
1175. 最大半连通子图
1175. 最大半连通子图 - AcWing题库
首先,强连通分量一定是半连通分量,所以可以先找出图中所有强连通分量
用tarjan将图缩点,得到由强连通分量组成的有向无环图,此时再找出极大半连通分量(有向图中点最多的一条路径),可以按照拓扑序递推,找一条最长路
由于每个点都是强连通分量,计算最长路的节点数量时,需要累加所有“节点”(强连通分量)中的节点数量,只能在按照拓扑序递推最长路时,将边权设置为分量中的点数
若缩点后的两点之间存在多条边,因为导出子图一定会将和点有关的所有边选择,所以边数不同不能算不同的半连通子图,半连通分量中不存在只选择两点之间一部分边的情况,因此点数不同才算不同的半连通子图
由于我们找最长路时,需要使用边的权重,重边将影响最长路的求解,所以在建立缩点后的图时要注意给边判重
边的权重是分量中点的数量,与这些两点之间的重边没有关系,因此只需要在两点之间建立一条边
缩点建图完成后,就是递推求最长路。由于缩点的递归顺序是拓扑序的逆序,所以我们逆着遍历缩点的顺序,按照拓扑序递推求最长路即可。注意不仅要记录最长路的权值还要记录最长路的数量,分别对应最大半连通子图中点的数量以及最大半连通子图的数量
#include <iostream>
#include <cstring>
#include <unordered_set>
using namespace std;typedef long long LL;
const int N = 1e5 + 10, M = 2e6 + 10;
int h[N], hs[N], e[M], ne[M], idx;
int dfn[N], low[N], cnt, tp;
int stk[N], tt; bool st[N];
unordered_set<LL> s;
int sz[N], id[N];
int f[N], g[N];
int n, m, X;void add(int h[], int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}void tarjan(int x)
{dfn[x] = low[x] = ++ tp;st[x] = true, stk[ ++ tt] = x;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!dfn[y]){tarjan(y);low[x] = min(low[x], low[y]);}else if (st[y]) low[x] = min(low[x], dfn[y]);}if (dfn[x] == low[x]){int y;cnt ++ ;do {y = stk[tt -- ], st[y] = false;id[y] = cnt;sz[cnt] ++ ;} while (x != y);}
}int main()
{memset(h, -1, sizeof(h));memset(hs, -1, sizeof(hs));scanf("%d%d%d", &n, &m, &X);int x, y;for (int i = 0; i < m; ++ i ){scanf("%d%d", &x, &y);add(h, x, y);}for (int i = 1; i <= n; ++ i )if (!dfn[i]) tarjan(i);for (int x = 1; x <= n; ++ x )for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];int a = id[x], b = id[y];if (a != b){LL t = a * 100000ll + b;if (!s.count(t)) {add(hs, a, b);s.insert(t);}}}for (int x = cnt; x; -- x ){if (!f[x]) f[x] = sz[x], g[x] = 1;for (int i = hs[x]; i != -1; i = ne[i]){int y = e[i];if (f[y] < f[x] + sz[y]){f[y] = f[x] + sz[y];g[y] = g[x];}else if (f[y] == f[x] + sz[y]) g[y] = (g[x] + g[y]) % X;}}int maxf = 0, sum = 0;for (int i = 1; i <= cnt; ++ i ){if (f[i] > maxf){maxf = f[i];sum = g[i];}else if (f[i] == maxf) sum = (sum + g[i]) % X;}printf("%d\n%d\n", maxf, sum);return 0;
}
debug:unordered_set比set快很多,当然,也比unordered_map快
最后的最长路递推没有按照拓扑序(cnt的逆序)
没有去重,递推时要遍历缩点后的图
递推时:
if (f[y] < f[x] + sz[y])
{f[y] = f[x] + sz[y];g[y] = g[x];
}
写成了g[y] = f[x],手滑了,但是这种错误真的超难debug
368. 银河
368. 银河 - AcWing题库
很直接的不等式关系,一眼差分约束,首先转换不等式关系,由于题目要求最小值,所以要用最短路,所有不等式要转换成>=的形式
- A >= B, B >= A
- B >= A + 1
- A >= B
- A >= B + 1
- B >= A
并且题目提供了一个边界, x i > = 1 x_i >= 1 xi>=1,转换成 x i > = x 0 + 1 x_i >= x_0 + 1 xi>=x0+1
那么 x 0 x_0 x0为虚拟源点,与所有点有一条边权为1的边,从 x 0 x_0 x0开始遍历,一定能遍历所有的点,也一定能遍历所有的边
所以从 x 0 x_0 x0为源点,用spfa求最长路,并且判断负环(无解)即可
这题和1169. 糖果一样,解法一样,数据一样,但是时间限制卡的很死。用sfpa求最长路与正环会超时
正解是:用线性时间复杂度的tarjan求强连通分量,判断每个强连通分量是否是正环。由于图中只有权值为0和1的边,环中权值为0是个零环,只要有一条边的权值为1,那么该强连通分量就是正环,返回无解
接着按照拓扑序求最长路即可
#include <iostream>
#include <cstring>
using namespace std;typedef long long LL;
const int N = 1e5 + 10, M = 4e5 + 10;
int h[N], hs[N], e[M], ne[M], w[M], idx;
int dfn[N], low[N], cnt, tp;
int stk[N], tt; bool st[N];
int id[N], dis[N], sz[N];
int n, m;void add(int h[], int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}void tarjan(int x)
{dfn[x] = low[x] = ++ tp;st[x] = true, stk[ ++ tt] = x;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!dfn[y]){tarjan(y);low[x] = min(low[x], low[y]);}else if (st[y]) low[x] = min(low[x], dfn[y]);}if (dfn[x] == low[x]) {int y;++ cnt;do {y = stk[tt -- ], st[y] = false;id[y] = cnt;sz[cnt] ++ ;} while (x != y);}
}int main()
{memset(h, -1, sizeof(h));memset(hs, -1, sizeof(hs));scanf("%d%d", &n, &m);int t, x, y;for (int i = 0; i < m; ++ i ){scanf("%d%d%d", &t, &x, &y);if (t == 1) add(h, x, y, 0), add(h, y, x, 0);else if (t == 2) add(h, x, y, 1);else if (t == 3) add(h, y, x, 0);else if (t == 4) add(h, y, x, 1);else add(h, x, y, 0);}for (int i = 1; i <= n; ++ i ) add(h, 0, i, 1);for (int i = 0; i <= n; ++ i ) if (!dfn[i]) tarjan(i);for (int x = 0; x <= n; ++ x )for (int i = h[x]; i != -1; i = ne[i]){int y= e[i];int a = id[x], b = id[y];if (a == b && w[i] == 1){puts("-1");return 0;}else if (a != b) add(hs, a, b, w[i]);}for (int x = cnt; x; -- x ){for (int i = hs[x]; i != -1; i = ne[i] ){int y = e[i];dis[y] = max(dis[y], dis[x] + w[i]);}}LL sum = 0;for (int i = 1; i <= cnt; ++ i ) sum += (LL)sz[i] * dis[i];printf("%lld\n", sum);return 0;
}
debug:递推时又是没有遍历hs,缩点后的图
虚拟源点的边没有提前建,之前做sfpa时习惯在spfa里直接将所有边入队了
同时,tarjan需要遍历的点为0n之间的所有点,不是1n
最后计算总和时,连通分量乘以距离才是正解
相关文章:

第三章 图论 No.9有向图的强连通与半连通分量
文章目录 定义Tarjan求SCC1174. 受欢迎的牛367. 学校网络1175. 最大半连通子图368. 银河 定义 连通分量是无向图的概念,yxc说错了,不要被误导 强连通分量:在一个有向图中,对于分量中的任意两点u,v,一定能从…...

回归预测 | MATLAB实现基于PSO-LSSVM-Adaboost粒子群算法优化最小二乘支持向量机结合AdaBoost多输入单输出回归预测
回归预测 | MATLAB实现基于PSO-LSSVM-Adaboost粒子群算法优化最小二乘支持向量机结合AdaBoost多输入单输出回归预测 目录 回归预测 | MATLAB实现基于PSO-LSSVM-Adaboost粒子群算法优化最小二乘支持向量机结合AdaBoost多输入单输出回归预测预测效果基本介绍模型描述程序设计参考…...

Mysql 和Oracle的区别
、mysql与oracle都是关系型数据库,Oracle是大型数据库,而MySQL是中小型数据库。但是MySQL是开源的,但是Oracle是收费的,而且比较贵。 1 2 mysql默认端口:3306,默认用户:root oracle默认端口&…...

在收藏夹里“积灰”的好东西——“收藏从未停止,行动从未开始”
方向一:分享一道你收藏的好题 小雅兰刚学数据结构与算法的时候,学的真的是很吃力,感觉链表真的特别的难,在学习了后面的知识之后,发现链表慢慢变得简单了,若是放在现在,小雅兰仍然觉得链表的知…...
【算法|数组】双指针
算法|数组——双指针 引入 给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。 示例 1: 输入:nums [-4,-1,0,3,10] 输出:[0,1,9,16,100] 解释:…...

asp.net core6 webapi 使用反射批量注入接口层和实现接口层的接口的类到ioc中
IBLL接口层类库 namespace IBLL {public interface ICar{string CarName();} } namespace IBLL {public interface IRed{string RedName();} }BLL实现接口层类库 namespace BLL {public class Car : ICar{public string CarName(){return "BBA";}} } namespace BLL…...

【2023】字节跳动 10 日心动计划——第九关
目录 1. 螺旋矩阵2. 划分字母区间3. 子集 II 1. 螺旋矩阵 🔗 原题链接:54. 螺旋矩阵 类似于BFS那样使用方向数组即可。 class Solution { public:vector<int> spiralOrder(vector<vector<int>>& matrix) {int m matrix.size(), …...
小龟带你敲排序之冒泡排序
冒泡排序 一. 定义二.题目三. 思路分析(图文结合)四. 代码演示 一. 定义 冒泡排序(Bubble Sort,台湾译为:泡沫排序或气泡排序)是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元…...
Nacos AP架构集群搭建(Windows)
手写SpringCloud项目地址,求个star github:https://github.com/huangjianguo2000/spring-cloud-lightweight gitee:https://gitee.com/huangjianguo2000/spring-cloud-lightweigh 目录: 一:初始化MySQL 二:复制粘贴三份Nacos文…...

nodejs+vue+elementui,图书评论管理系统_g9e3a
用户的功能主要是对首页、图书信息、公告信息、在线咨询、个人中心等进行操作。表名:token语言 node.js 框架:Express 前端:Vue.js 数据库:mysql 数据库工具:Navicat 开发软件:VScode 前端nodejsvueelementui, 管理员…...
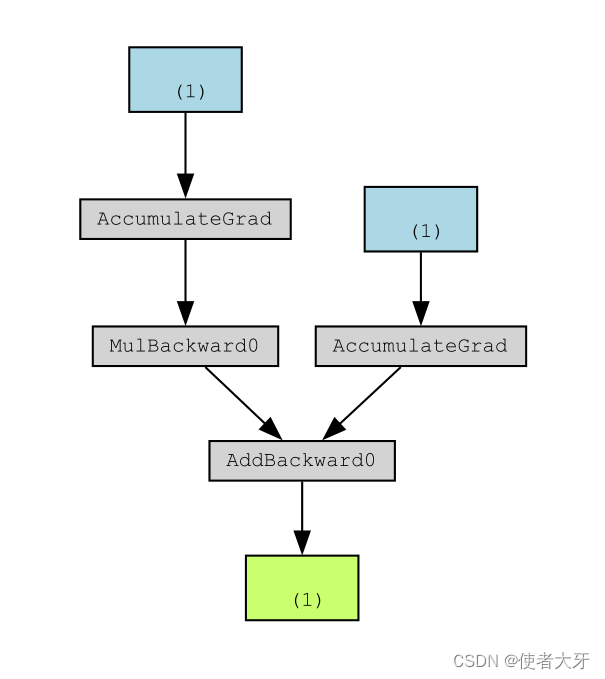
基于TorchViz详解计算图(附代码)
文章目录 0. 前言1. 计算图是什么?2. TorchViz的安装3. 计算图详解 0. 前言 按照国际惯例,首先声明:本文只是我自己学习的理解,虽然参考了他人的宝贵见解,但是内容可能存在不准确的地方。如果发现文中错误,…...

解决GitHub的速度很慢的几种方式
1. GitHub 镜像访问 这里提供两个最常用的镜像地址: https://hub.njuu.cf/search https://www.gitclone.com/gogs/search/clonesearch 也就是说上面的镜像就是一个克隆版的 GitHub,你可以访问上面的镜像网站,网站的内容跟 GitHub 是完整同步…...
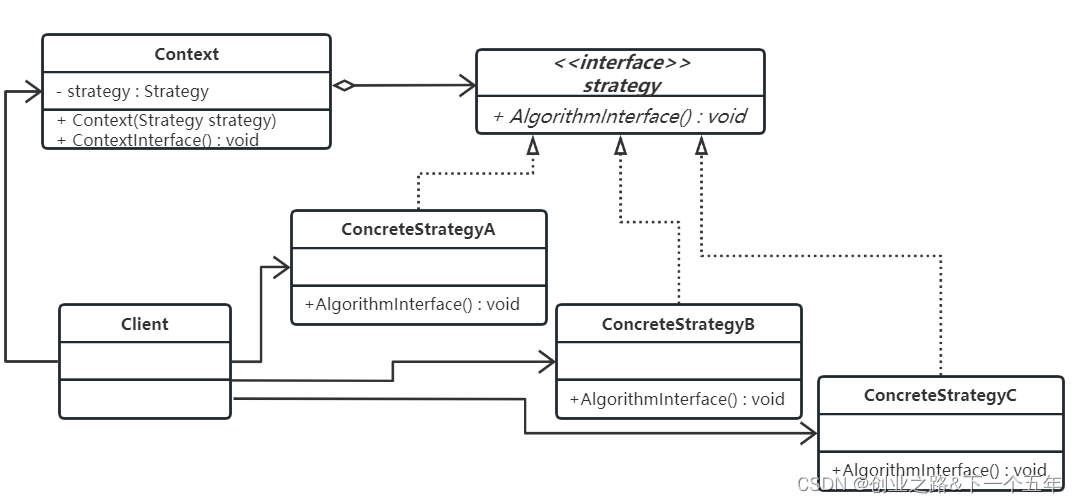
设计模式再探——策略模式
目录 一、背景介绍二、思路&方案三、过程1.策略模式简介2.策略模式的类图3.策略模式代码4.策略模式还可以优化的地方5.策略模式的例子改造(配置文件反射) 四、总结五、升华 一、背景介绍 最近在做产品的过程中,对于主题讨论回复内容,按照追评次数排…...
基于Googlenet深度学习网络的人员行为动作识别matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 1. 原理 1.1 深度学习与卷积神经网络(CNN) 1.2 GoogLeNet 2. 实现过程 2.1 数据预处理 2.2 构建网络模型 2.3 数据输入与训练 2.4 模型评估与调优 3. 应用领域…...

存储过程的学习
1,前言 这是实习期间学习的,我可能是在学校没好好听课,(或者就是学校比较垃,没教这部分,在公司经理让我下去自己学习,太难了,因为是公司代码很多部分都是很多表的操作&#…...

zookeeperAPI操作与写数据原理
要执行API操作需要在idea中创建maven项目 (改成自己的阿里仓库)导入特定依赖 添加日志文件 上边操作做成后就可以进行一些API的实现了 目录 导入maven依赖: 创建日志文件: 创建API客户端: (1)…...

防火墙对双通道协议的处理
防火墙是一种网络安全设备或软件,用于控制网络流量并保护计算机网络免受未经授权的访问、恶意攻击和网络威胁。它作为网络的第一道防线,用于监视、过滤和管理进出网络的数据包。 防火墙可以基于预设的安全策略对网络流量进行评估和筛选。它通过比较数据…...
vscode搭建c语言环境问题
c语言环境搭建参考文章:【C语言初级阶段学习1】使用vscode运行C语言,vscode配置环境超详细过程(包括安装vscode和MinGW-W64安装及后续配置使用的详细过程,vscode用户代码片段的使用)[考研专用]_QAQshift的博客-CSDN博客 问题如下:…...
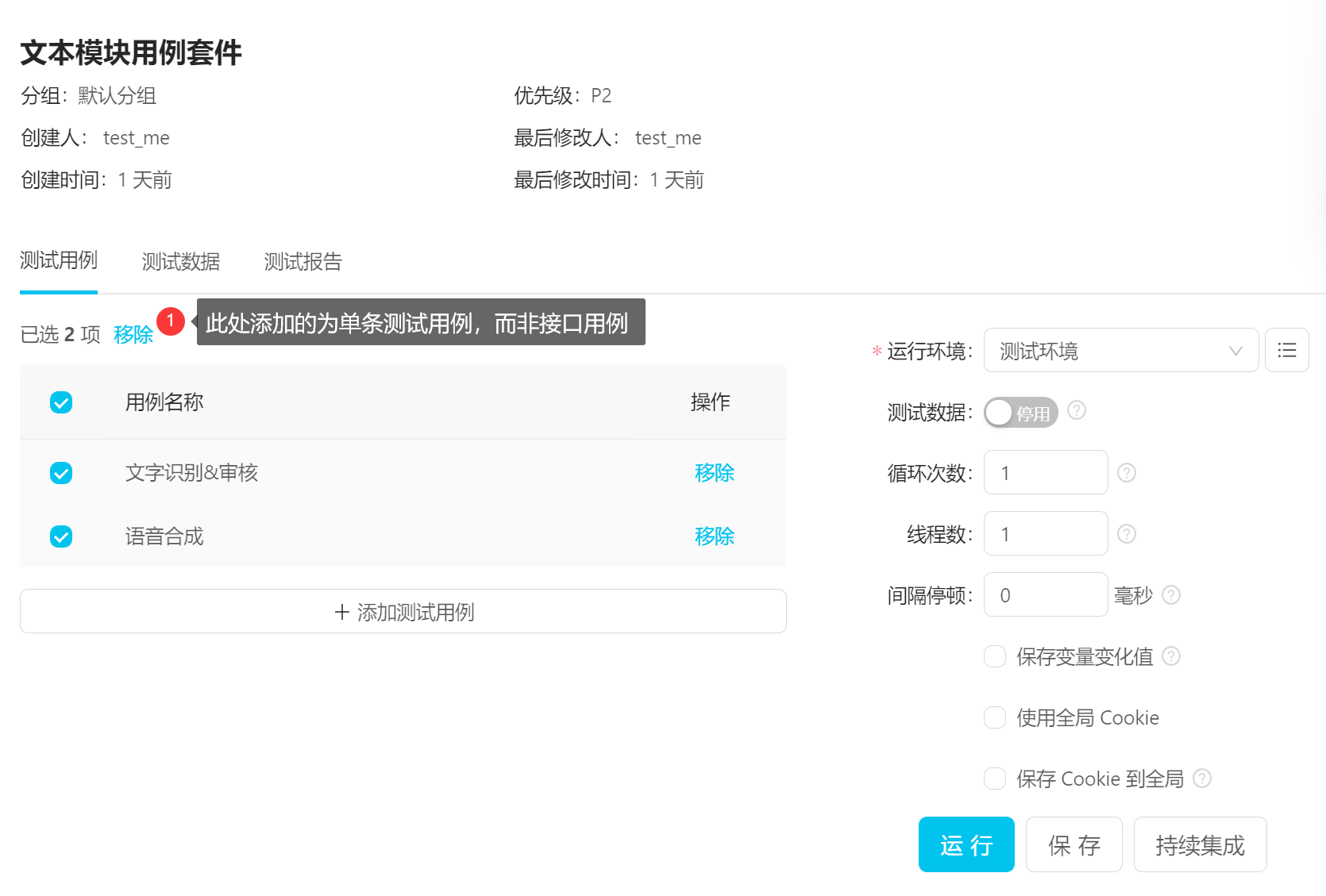
全网最全的接口自动化测试教程
为什么要做接口自动化 相对于UI自动化而言,接口自动化具有更大的价值。 为了优化转化路径或者提升用户体验,APP/web界面的按钮控件和布局几乎每个版本都会发生一次变化,导致自动化的代码频繁变更,没有起到减少工作量的效果。 而…...
数据结构----结构--线性结构--链式存储--链表
数据结构----结构–线性结构–链式存储–链表 1.链表的特点 空间可以不连续,长度不固定,相对于数组灵活自由 搜索: 时间复杂度O(n) 增删: 头增头删时间复杂度O(1) 其他时间复杂度为O(n) 扩展:单向循环链表的特性 从任意节…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
