【数据结构】树和二叉树的概念及结构
1.树概念及结构
1.1树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 有一个特殊的结点,称为根结点,根节点没有前驱结点。
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继。
- 因此,树是递归定义的。

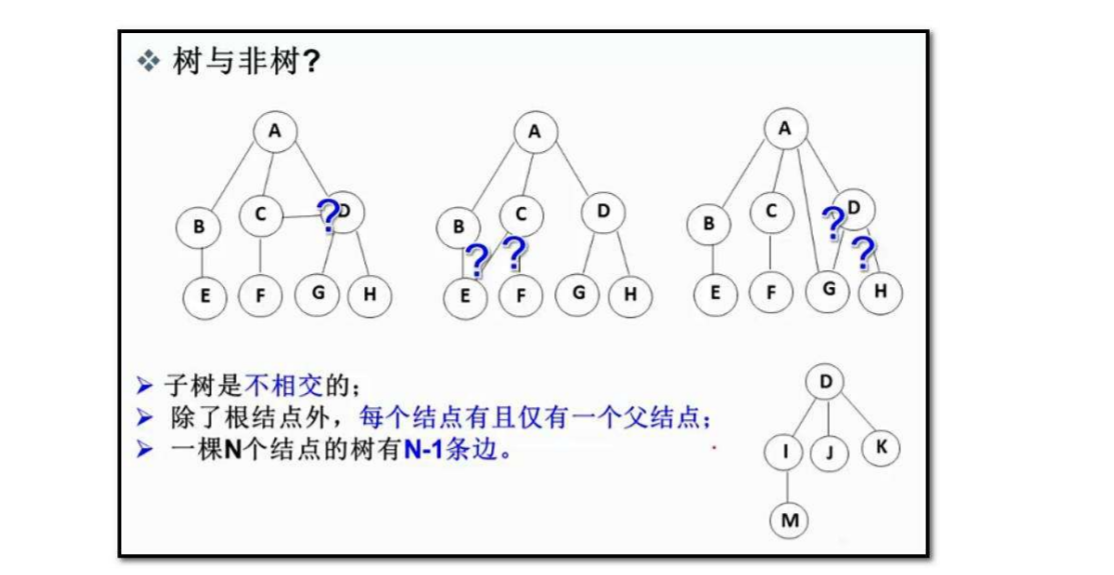
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
1.2 树的相关概念
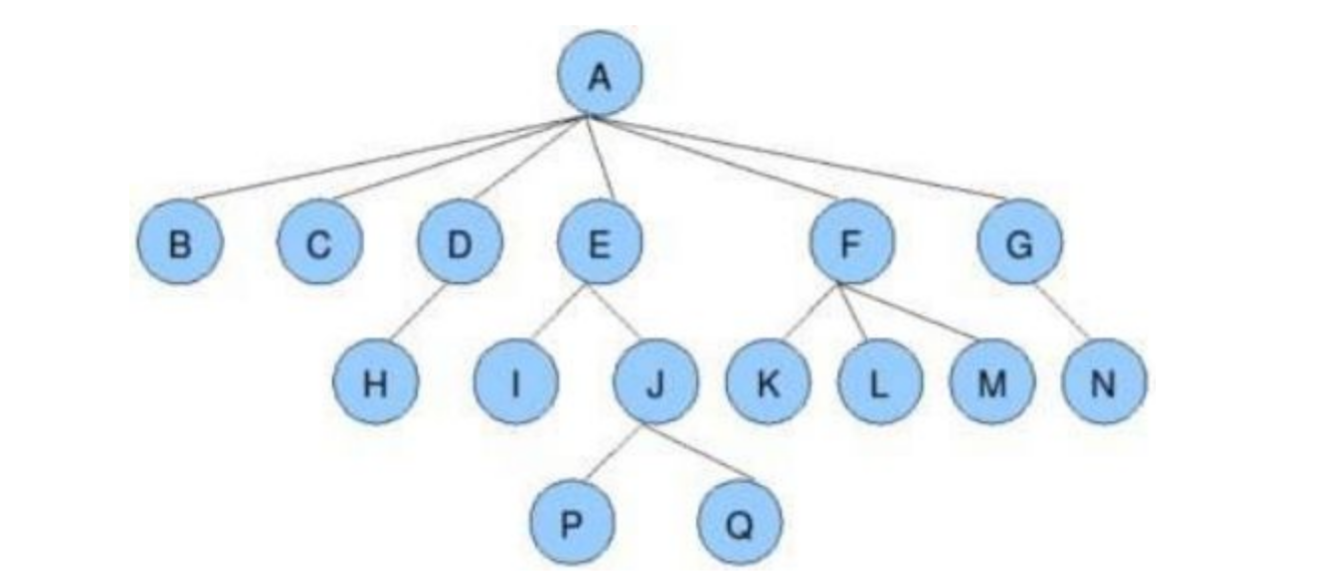
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林;
1.3 树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
树的孩子兄弟表示法(Child-sibling representation)也被称为左孩子右兄弟表示法,它是一种用于表示树结构的方法。在这种表示法中,每个节点包含两个指针:一个指向其第一个子节点,另一个指向它的下一个兄弟节点。
typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域
};
1.4 树在实际中的运用(表示文件系统的目录树结构)

2.二叉树概念及结构
2.1概念
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成

从上图可以看出:
1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的二叉树都是由以下几种情况复合而成的:
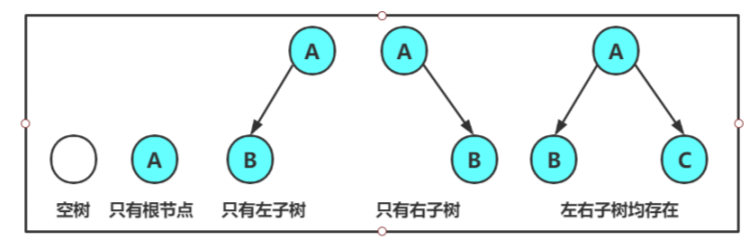
2.2 特殊的二叉树
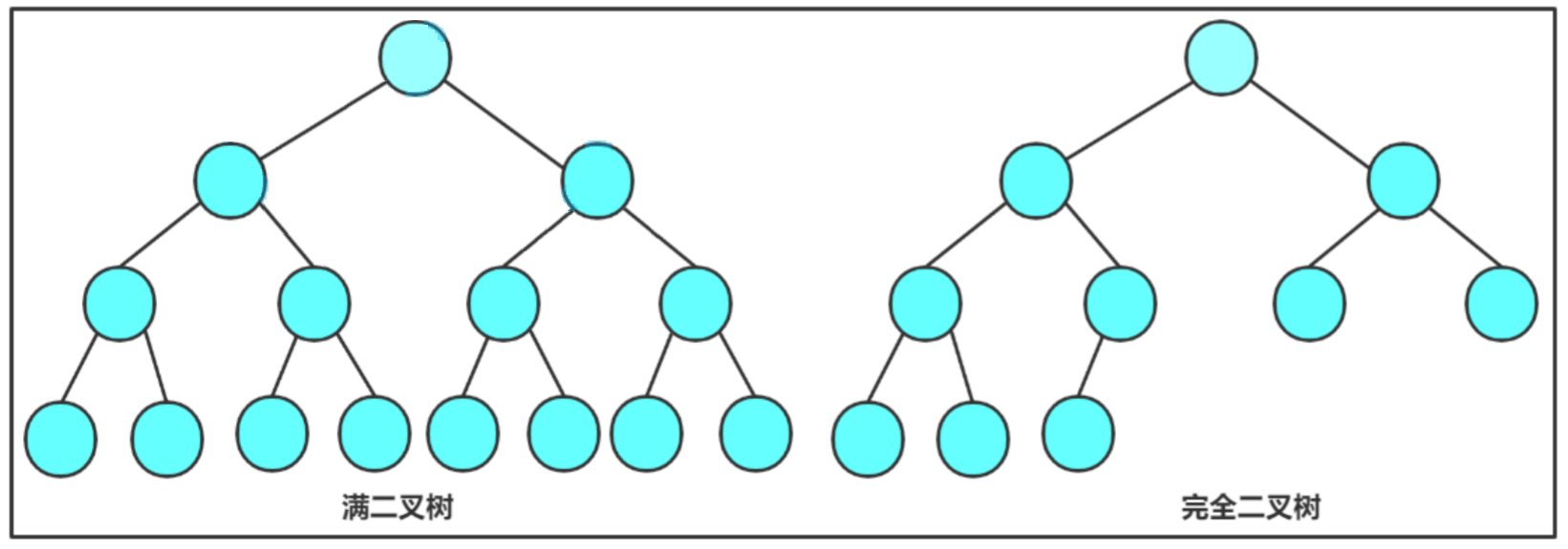
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是![]() ,则它就是满二叉树。
,则它就是满二叉树。
2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
2.3 二叉树的性质

1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )
A 不存在这样的二叉树
B 200
C 198
D 199
解析:叶子节点是度为0的节点,根据上面的性质3:
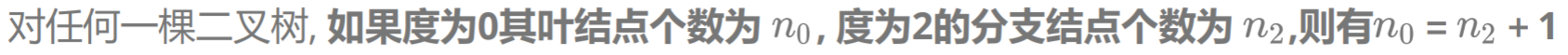
所以叶子节点=199+1=200;
答案:B
2.在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A n
B n+1
C n-1
D n/2解析:

答案:B
3.一棵完全二叉树的节点数位为531个,那么这棵树的高度为( )
A 11
B 10
C 8
D 12 解析:
答案:B
4.一个具有767个节点的完全二叉树,其叶子节点个数为()
A 383
B 384
C 385
D 386解析:
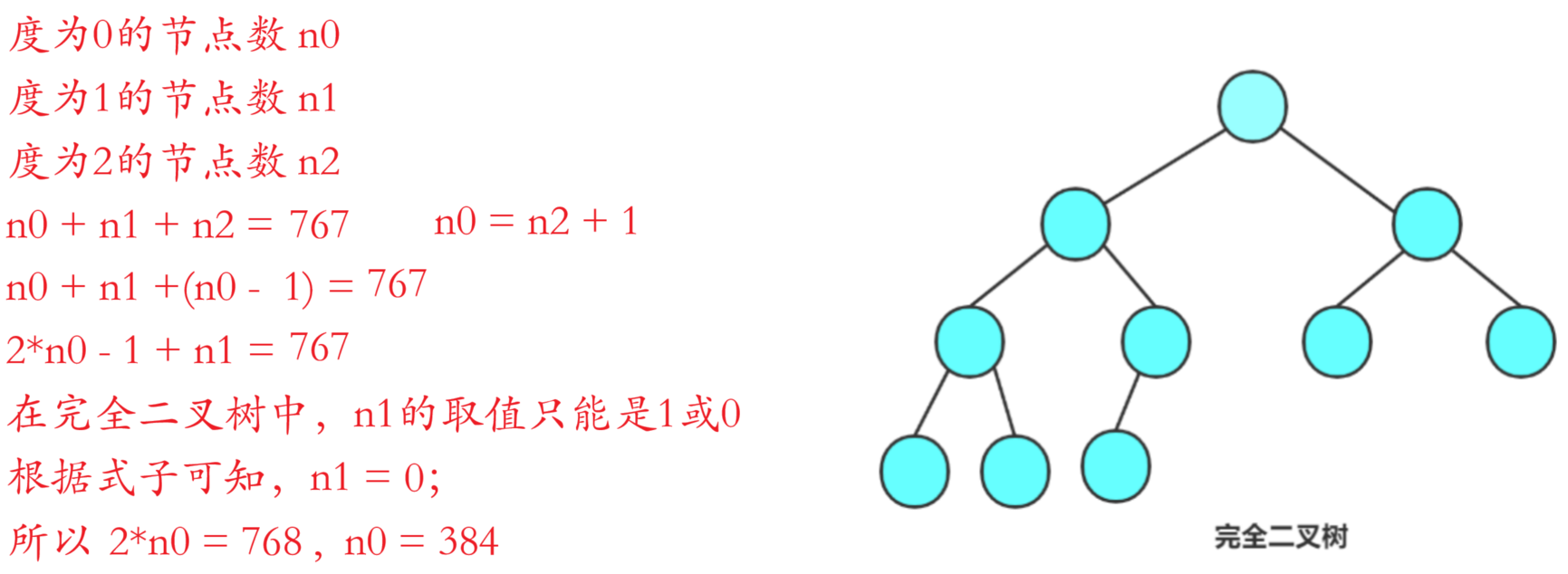
答案:B
2.4 二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
1. 顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数,在逻辑上是一颗二叉树。


2. 链式存储
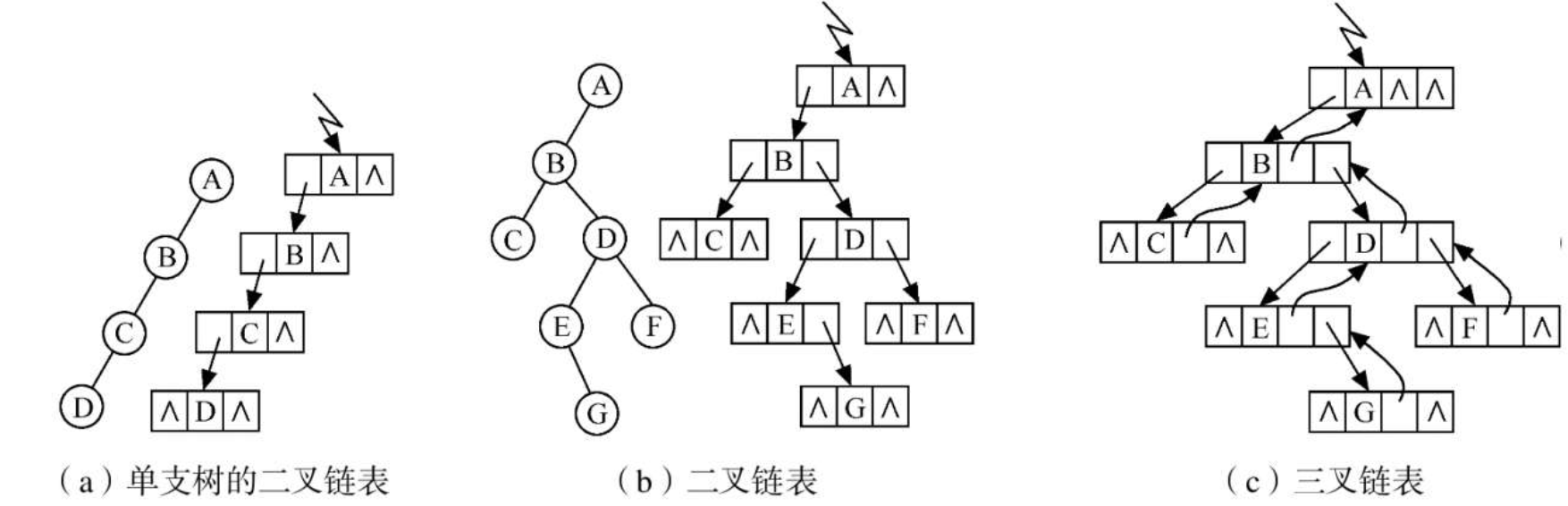
二叉树的链式存储结构是指:用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,到高阶数据结构如红黑树等会用到三叉链。

相关文章:

【数据结构】树和二叉树的概念及结构
1.树概念及结构 1.1树的概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。 有一个特殊的结点&#…...

8.1.tensorRT高级(3)封装系列-模型编译过程封装,简化模型编译代码
目录 前言1. 模型编译过程封装2. 问答环节总结 前言 杜老师推出的 tensorRT从零起步高性能部署 课程,之前有看过一遍,但是没有做笔记,很多东西也忘了。这次重新撸一遍,顺便记记笔记。 本次课程学习 tensorRT 高级-模型编译过程封装…...

化工行业案例 | 甄知科技助力万华化学重构IT服务价值,打造信息中心ERP!
随着科技的发展,新材料的应用领域与日俱增,近年来,全球化工新材料产业发展整体步入高技术引领、产品迭代速度快、产业规模和需求不断扩大的阶段。一体化协同与数字化转型策略是实现化工新材料生产原料自给、节能降耗、降低排放和物料成本的重…...
day6 STM32时钟与定时器
STM32时钟系统的概述 概念 时钟系统是由振荡器(信号源)、定时唤醒器、分频器等组成的电路。 常用的信号有晶体振荡器和RC振荡器。 意义 时钟是嵌入式系统的脉搏,处理器内核在时钟驱动下完成指令执行,状态变换等动作ÿ…...

【JavaEE进阶】SpringBoot 配置文件
文章目录 SpringBoot配置文件1. 配置文件的作用2. 配置文件的格式3. properties 配置文件说明3.1 properties 基本语法3.2 读取配置文件3.3 properties 优缺点分析 4. yml配置文件说明4.1 yml 基本语法4.2 yml 配置读取 5. properties和yml的对比 SpringBoot配置文件 1. 配置文…...

ResNet创新点总结
ResNet(Residual Networks)是深度学习中的一个重要架构,其创新点主要体现在解决了深层神经网络训练中的梯度消失和梯度爆炸问题,从而使得可以构建更深的神经网络。以下是 ResNet 的创新点总结: 1. 残差连接&#x…...
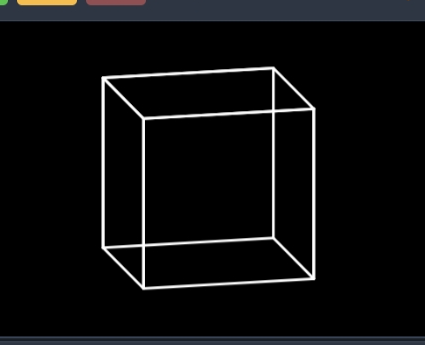
Scratch 之 3D 介绍及教程
第一章 为什么 3D 很难? 1.1 3D 难在何处? 3D 之所以会使我们觉得困难,是因为 Scratch 软件只有两个坐标轴,既:X轴、Y轴。 2维坐标系 而 3D 却拥有三个坐标轴: 3维坐标系 怎么办?很简单&…...

最强自动化测试框架Playwright(19)- 事件
Playwright允许收听网页上发生的各种类型的事件,例如网络请求,创建子页面,专用工作人员等。有几种方法可以订阅此类事件,例如等待事件或添加或删除事件侦听器。 等待事件 大多数情况下,脚本需要等待特定事件的发生。…...

静态网页和动态网页区别
1,静态网页和动态网页有何区别 1) 更新和维护 静态网页内容一经发布到网站服务器上,无论是否有用户访问,这些网页内容都是保存在网站服务器上的。如果要修改网页的内容,就必须修改其源文件,然后重新上传到服务器上。…...

美国服务器有哪些类型?
美国服务器有哪些类型?常见的服务器可分为虚拟主机、云服务器、物理服务器以及高防服务器,在海外服务器之中,使 用较多的属于美国服务器,下面我们就一起看看美国服务器有哪些及常见的美国服务器。 美国服务器有哪些? 与服务器一样&am…...

【基因检测人工智能】如何使用JAVASCRIPT在HTML文档内部增加一个段落
【基因检测人工智能】如何使用JAVASCRIPT在HTML文档内部增加一个段落 目的:采用JAVASCRIPT在一个HTML网页中增加一个段落。 下面是原来的HTML代码部分: <!DOCTYPE html> <html lang"zh-Hans"><head><meta charset&quo…...

unittest单元测试
当你在编写测试用例时,可以使用Python内置的unittest模块来进行单元测试。下面是一个逐步指南,帮助你理解如何编写和运行基本的单元测试。 导入必要的模块: 首先,你需要导入unittest模块和需要测试的模块(例如…...
每天一道leetcode:72. 编辑距离(动态规划困难)
今日份题目: 给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。 你可以对一个单词进行如下三种操作: 插入一个字符 删除一个字符 替换一个字符 示例1 输入:word1 "horse", word…...

详细介绍如何使用 OpenCV 对图像进行锐化
将了解锐化图像的过程,我们将使用内核来突出显示每个特定像素并增强其发出的颜色。它与模糊过程非常相似,只不过现在我们不是创建一个内核来平均每个像素强度,而是创建一个内核,该内核将使像素强度更高,因此对人眼来说更加突出。 了解流程的后端。 很高兴知道内核用于模糊…...
Java代理模式——静态代理与动态代理
代理模式 代理模式允许你为其他对象提供一个代理,以控制对这个对象的访问。代理模式在不改变实际对象的情况下,可以在访问对象时添加额外的功能。 可以理解为代理模式为被代理对象创造了一个替身,调用者可以通过这个替身去实现这个被代理对…...

Vue day02 Computed和Watch
1.事件绑定 可以用 v-on 指令监听DOM 事件,并在触发时运行一些 JavaScript 代码。v-on 还可以接收一个需要调用的方法名称。 <button v-on:click"handler">good</button> methods: { handler: function (event) { if (event) { alert(event.t…...
【Java】一只小菜坤的编程题之旅【3】
文章目录 1丶判定是否互为字符重排2、杨辉三角3丶某公司的1个面试题(字符串包含问题) 1丶判定是否互为字符重排 这个题我们用一个非常简单的思想就能实现,我们先将字符串转换为字符数组,然后对字符数组进行排序,然后再…...
)
全面掌握 Jaeger 分布式调用链路跟踪理论和实战,Go 为所有使用 go-resty 库发起 HTTP 请求集成链路跟踪 jaeger(附源码)
全面掌握 Jaeger 分布式调用链路跟踪理论和实战,Go 为所有使用 go-resty 库发起 HTTP 请求集成链路跟踪 jaeger(附源码)。 介绍一个开源的分布式跟踪系统 Jaeger,首先从理论基础知识开始学习,将学习如何在 HTTP 请求中集成链路跟踪,以及如何在 GORM 框架实现,最后学习 …...

vue键盘和鼠标事件
1、键盘事件 **按Enter键** keyup.enter**按PageDown键** keyup.page-down **按Tab键** keyup.tab **按Delete键** keyup.delete **按ESC键** keyup.esc**按Space键** keyup.space **按↑(Up)键** keyup.up**按↓(Down)键** keyup…...

Chrome 手动代理设置 HTTP/Socks5
1、安装代理插件:SwitchyOmega 在线安装 从 Chrome 应用商店 安装,如果您无法从该链接安装,请使用下面的离线安装。 离线安装 ①、去 Github 下载 最新版安装包 ,或者直接 本地下载 文件进行安装。 ②、下载安装文件后…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

