迪瑞克斯拉算法
迪锐克斯拉算法
简单来说就是在有向图中,给定一个图中具体的出发点,从这个点出发能够到达的所有的点,每个点的最短距离是多少。到不了的点,距离则是正无穷。有向,无负权重,可以有环。
所以说,迪锐克斯拉算法是生成一个从源点出发到各个点的最小距离表。
举例:有向图如图所示
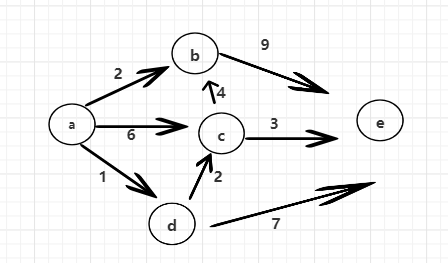
从给定的出发点a出发,最终要获得的是a到b,c,d,e每个点之间的最短距离。默认a到自己的距离是0,其他的点还没到达的点的距离是正无穷。已经确定的答案不动,在没有确定的记录中找一个最小的出来。
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 正无穷 | 正无穷 | 正无穷 | 正无穷 |
所以先从a点出发的三条边1,2,6。中找出权重为1的边,ad距离为1,小于之前的正无穷(比之前距离小),所以更新a到d之间的距离,bcd同理。所以更新完后距离如下:
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 2 | 6 | 1 | 正无穷 |
此时,从a出发的三条边已经走完,所以a点确定下来,再也不动。
其余没有确定的记录中d是最短的(从a出发到b的距离为1),所以从d开始向下找(d属于中间的跳点)。
d出发的边有两条,分别是dc和de。其中dc距离为2,再加上之前a到d的距离为1,所以此时a到c的距离经过d跳转后为3,小于之前的6,所以更新ac之间距离,同样de距离7小于正无穷。所以也进行更新。d也确定了。
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 2 | 3 | 1 | 7 |
接下来从不确定的记录中根据最小的向下找。b点出发的边有一条be,be距离9加上a到b的距离2,所以be距离为11,大于之前的,不更新。b也确定了。
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 2 | 3 | 1 | 7 |
还剩下c,从c点出发的边有两条,cb和ce,因为b点已经确定了不再动,所以一看ce一条,ce距离为3,a到c距离为3,所以ae之间距离为6,小于之前,更新e点距离。
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 2 | 3 | 1 | 6 |
代码
根据上面的分析进行代码的实现,不过getMinDistanceAndUnSelectNode有瑕疵,因为每找一个minNode就会在集合中都遍历一次。会在下面进行代码优化。
public static HashMap<Node, Integer> dijkstra1(Node from) {HashMap<Node, Integer> distanceMap = new HashMap<>();distanceMap.put(from, 0);//已经确定的边;HashSet<Node> selectedNodes = new HashSet<>();//根据已经确定的记录 和 map,找出没确定的中最小的记录Node minNode = getMinDistanceAndUnSelectNode(distanceMap, selectedNodes);while (minNode != null) {int distance = distanceMap.get(minNode);for (Edge edge : minNode.edges) {Node toNode = edge.to;if (!distanceMap.containsKey(toNode)) {distanceMap.put(toNode, distance + edge.weight);} else {//edge.weight + distance 当前边的权重 + 我此时当做跳点的距离。//distanceMap.get(toNode) 已经存在的距离distanceMap.put(toNode, Math.min(distanceMap.get(toNode), (edge.weight + distance)));}}//所有的边都已经遍历完,这个点可以确定了,放到确定的集合中。selectedNodes.add(minNode);//再次获取最小的记录minNode = getMinDistanceAndUnSelectNode(distanceMap, selectedNodes);}return distanceMap;}public static Node getMinDistanceAndUnSelectNode(HashMap<Node, Integer> distanceMap, HashSet<Node> selectedNode) {Node minNode = null;int minDistance = Integer.MAX_VALUE;for (Map.Entry<Node, Integer> entry : distanceMap.entrySet()) {Node node = entry.getKey();int distance = entry.getValue();if (!selectedNode.contains(node) && distance < minDistance) {minDistance = distance;minNode = node;}}return minNode;}
相关文章:

迪瑞克斯拉算法
迪锐克斯拉算法 简单来说就是在有向图中,给定一个图中具体的出发点,从这个点出发能够到达的所有的点,每个点的最短距离是多少。到不了的点,距离则是正无穷。有向,无负权重,可以有环。 所以说,迪…...
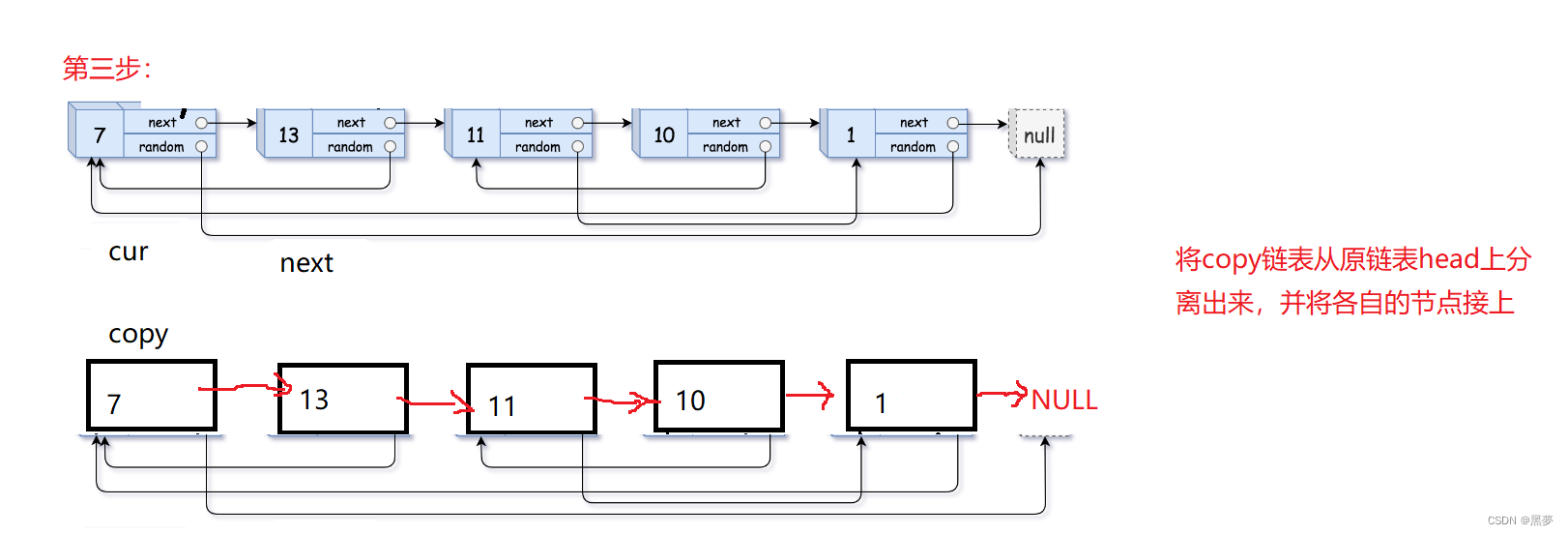
数据结构:力扣OJ题(每日一练)
目录 题一:环形链表 思路一: 题二:复制带随机指针的链表 思路一: 本人实力有限可能对一些地方解释的不够清晰,可以自己尝试读代码,望海涵! 题一:环形链表 给定一个链表的头节点…...

【论文阅读】基于深度学习的时序预测——Informer
系列文章链接 论文一:2020 Informer:长时序数据预测 论文二:2021 Autoformer:长序列数据预测 论文三:2022 FEDformer:长序列数据预测 论文四:2022 Non-Stationary Transformers:非平…...

机器学习 | Python实现GBDT梯度提升树模型设计
机器学习 | Python实现GBDT梯度提升树模型设计 目录 机器学习 | Python实现GBDT梯度提升树模型设计基本介绍模型描述模型使用参考资料基本介绍 机器学习 | Python实现GBDT梯度提升树模型设计。梯度提升树(Grandient Boosting)是提升树(Boosting Tree)的一种改进算法,GBDT也…...
elementUi表单恢复至初始状态并不触发表单验证
elementUi表单恢复至初始状态并不触发表单验证 1.场景再现2.解决方法 1.场景再现 左侧是树形列表,右侧是显示节点的详情,点击按钮应该就是新增一个规则的意思,表单内容是没有改变的,所以就把需要把表单恢复至初始状态并不触发表单…...
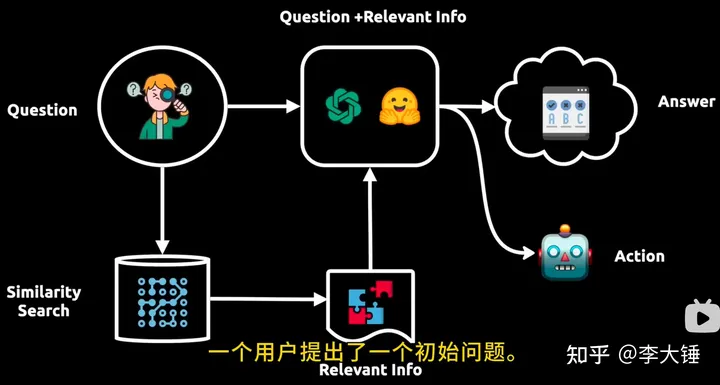
大模型相关知识
一. embedding 简单来说,embedding就是用一个低维的向量表示一个物体,可以是一个词,或是一个商品,或是一个电影等等。这个embedding向量的性质是能使距离相近的向量对应的物体有相近的含义,比如 Embedding(复仇者联盟)…...

无法在 macOS Ventura 上启动 Multipass
异常信息 ➜ ~ sudo multipass authenticate Please enter passphrase: authenticate failed: Passphrase is not set. Please multipass set local.passphrase with a trusted client. ➜ ~ multipass set local.passphrase Please enter passphrase: Please re-enter…...

算法通关村第六关——原来如此简单
层次遍历:又叫广度优先遍历。就是从根节点开始,先访问根节点下面一层全部元素,再访问之后的层次,直到访问完二叉树的最后一层。 我们先看一下基础的层次遍历题,力扣102题:给你一个二叉树,请你返…...
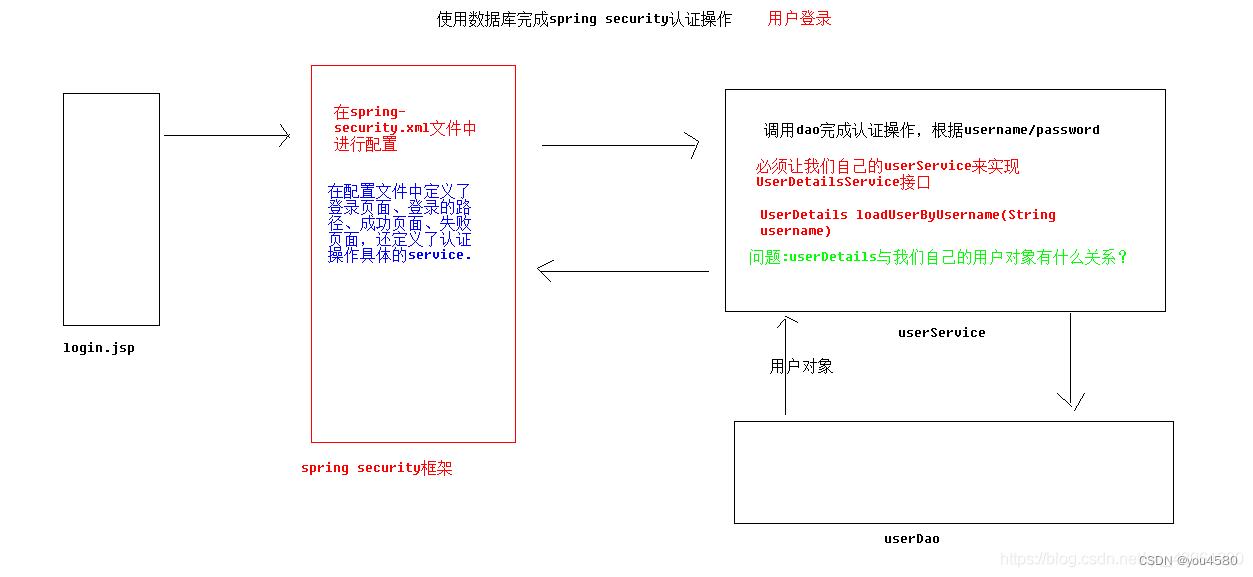
企业权限管理(八)-登陆使用数据库认证
Spring Security 使用数据库认证 在 Spring Security 中如果想要使用数据进行认证操作,有很多种操作方式,这里我们介绍使用 UserDetails 、 UserDetailsService来完成操作。 UserDetails public interface UserDetails extends Serializable { Collecti…...
第一百二十五天学习记录:C++提高:STL-deque容器(下)(黑马教学视频)
deque插入和删除 功能描述: 向deque容器中插入和删除数据 函数原型: 两端插入操作: push_back(elem); //在容器尾部添加一个数据 push_front(elem); //在容器头部插入一个数据 pop_back(); //删除容器最后一个数据 pop_front(); //删除容器…...

案例12 Spring MVC入门案例
网页输入http://localhost:8080/hello,浏览器展示“Hello Spring MVC”。 1. 创建项目 选择Maven快速构建web项目,项目名称为case12-springmvc01。 2.配置Maven依赖 <?xml version"1.0" encoding"UTF-8"?><project xm…...

【React】精选10题
1.React Hooks带来了什么便利? React Hooks是React16.8版本中引入的新特性,它带来了许多便利。 更简单的状态管理 使用useState Hook可以在函数组件中方便地管理状态,避免了使用类组件时需要继承React.Component的繁琐操作。 避免使用类组件…...

VS Spy++进程信息获取
查看进程中窗口信息。 Spy使用介绍 Windows下的程序及热键监视神器——Spy Word进程获取...
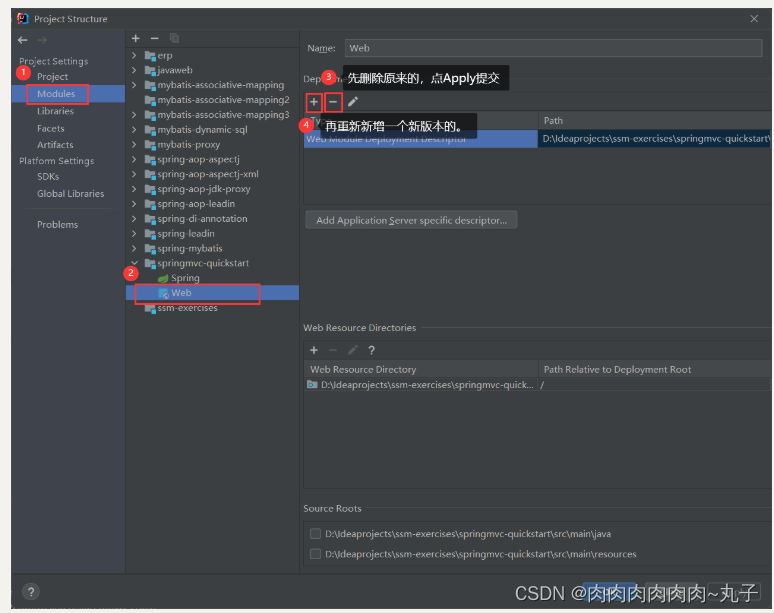
Java课题笔记~ SpringMVC概述
1.1 SpringMVC简介 SpringMVC 也叫Spring web mvc。是Spring 框架的一部分,在Spring3.0 后发布的。 1.2 SpringMVC的优点 基于MVC 架构 基于 MVC 架构,功能分工明确。解耦合。 容易理解,上手快,使用简单 就可以开发一个注解…...

SOPC之NIOS Ⅱ遇到的问题
记录NIOS Ⅱ中遇到的报错 一、NIOS II中Eclipse头文件未找到 问题:Unresolved inclusion: "system.h"等 原因:编译器无法找到头文件所在路径 解决方法: 在文件夹中找到要添加的头文件,并记录下其路径,如…...

uniapp uni-datetime-picker 日期和光标靠右
如果想在uni-datetime-picker组件中将日期和光标靠右,您可以使用自定义样式来实现。首先,您需要在页面的样式文件中定义一个类,用于定制uni-datetime-picker组件的样式。例如,你可以在App.vue或者页面的样式文件中添加以下代码&am…...

关于axios请求中的GET、POST、PUT、DELETE的一些认知
这篇写的特别好。而本文主要从实习用途中展开,不专业。 浅谈HTTP中Get、Post、Put与Delete的区别 1、Get 1、目前Get禁止使用requestBody形式传递值,如果使用了,后端会一直报错,让你确认是否有传递参数。 2、举例,模…...
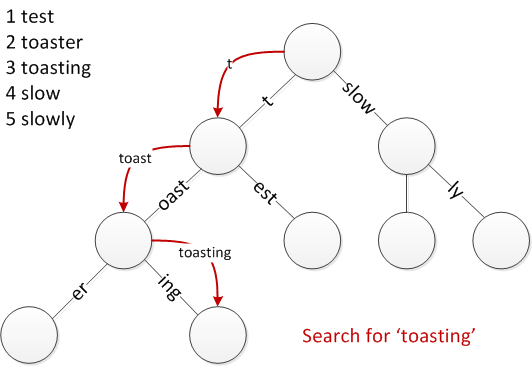
go-zero 是如何做路由管理的?
原文链接: go-zero 是如何做路由管理的? go-zero 是一个微服务框架,包含了 web 和 rpc 两大部分。 而对于 web 框架来说,路由管理是必不可少的一部分,那么本文就来探讨一下 go-zero 的路由管理是怎么做的,…...

Springboot集成ip2region离线IP地名映射-修订版
title: Springboot集成ip2region离线IP地名映射 date: 2020-12-16 11:15:34 categories: springboot description: Springboot集成ip2region离线IP地名映射 1. 背景2. 集成 2.1. 步骤2.2. 样例2.3. 响应实例DataBlock2.4. 响应实例RegionAddress 3. 打开浏览器4. 源码地址&…...
智能驾驶系列报告之一:智能驾驶 ChatGPT时刻有望来临
原创 | 文 BFT机器人 L3 功能加速落地,政策标准有望明确 L2 发展日益成熟,L3 功能加速落地。根据市场监管总局发布的《汽车驾驶自动化分级》与 SAE发布的自动驾驶分级标准,自动驾驶主要分为 6 个级别(0 级到 5 级,L0 …...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
