概率论:多维随机变量及分布
多维随机变量及分布
X X X为随机变量, ∀ x ∈ R , P { X ≤ x } = F ( x ) \forall x\in R,P\{X\le x\}=F(x) ∀x∈R,P{X≤x}=F(x)
设 F ( x ) F(x) F(x)为 X X X的分布函数,则
(1) 0 ≤ F ( x ) ≤ 1 0\le F(x)\le1 0≤F(x)≤1
(2) F ( x ) F(x) F(x)不减
(3) F ( x ) F(x) F(x)右连续
(4) F ( − ∞ ) = 0 , F ( + ∞ ) = 1 F(-\infin)=0,F(+\infin)=1 F(−∞)=0,F(+∞)=1
二维随机变量及分布
1.基本概念
二维随机变量, E E E为随机实验, Ω \Omega Ω为样本空间,若 ∀ ω ∈ Ω \forall\omega\in\Omega ∀ω∈Ω, ∃ \exists ∃唯一一对实数 ( X , Y ) (X,Y) (X,Y)与 ω \omega ω对应,称 ( X , Y ) (X,Y) (X,Y)为二维随机变量
2.分布函数
(1) ∀ x , y ∈ R , P { X ≤ x , Y ≤ y } = F ( x , y ) \forall x,y\in R,P\{X\le x,Y\le y\}=F(x,y) ∀x,y∈R,P{X≤x,Y≤y}=F(x,y)
(2) ( X , Y ) (X,Y) (X,Y)为二维随机变量
P { X ≤ x } = F X ( x ) P\{X\le x\}=F_X(x) P{X≤x}=FX(x), X X X的边缘分布函数
P { Y ≤ y } = F Y ( y ) P\{Y\le y\}=F_Y(y) P{Y≤y}=FY(y), Y Y Y的边缘分布函数
(3) ( X , Y ) (X,Y) (X,Y)为二维随机变量
设 F ( x , y ) F(x,y) F(x,y)为二维随机变量 ( X , Y ) (X,Y) (X,Y)的联合分布函数,则
(1) 0 ≤ F ( x , y ) ≤ 1 0\le F(x,y)\le1 0≤F(x,y)≤1
(2) F ( x , y ) F(x,y) F(x,y)关于 x , y x,y x,y不减
(3) F ( x ) F(x) F(x)关于 x , y x,y x,y右连续
(4) F ( − ∞ , − ∞ ) = 0 , F ( − ∞ , + ∞ ) = 0 , F ( + ∞ , − ∞ ) = 0 F(-\infin,-\infin)=0,F(-\infin,+\infin)=0,F(+\infin,-\infin)=0 F(−∞,−∞)=0,F(−∞,+∞)=0,F(+∞,−∞)=0
F ( + ∞ , + ∞ ) = 1 F(+\infin,+\infin)=1 F(+∞,+∞)=1
二维离散型变量及分布
1.二维离散型变量
( X , Y ) (X,Y) (X,Y)为二维随机变量,若 ( X , Y ) (X,Y) (X,Y)可能取值为有限个或可列个,称 ( X , Y ) (X,Y) (X,Y)为二维离散型变量
2.二维离散型变量联合分布律与边缘分布律
( X , Y ) (X,Y) (X,Y)为二维联合分布函数为 P { X ≤ x , Y ≤ y } = F ( x , y ) P\{X\le x,Y\le y\}=F(x,y) P{X≤x,Y≤y}=F(x,y)
若 ∃ f ( x , y ) ≥ 0 \exists f(x,y)\ge 0 ∃f(x,y)≥0使得 ∫ − ∞ x d x ∫ − ∞ y f ( x , y ) d y = F ( x , y ) \int_{-\infin}^{x}dx\int_{-\infin}^yf(x,y)dy=F(x,y) ∫−∞xdx∫−∞yf(x,y)dy=F(x,y)
称 ( X , Y ) (X,Y) (X,Y)为二维连续型变量, f ( x , y ) f(x,y) f(x,y)称为 ( X , Y ) (X,Y) (X,Y)的联合密度函数( f ( x , y ) ≥ 0 且 ∫ − ∞ ∞ d x ∫ − ∞ ∞ f ( x , y ) d y = 1 f(x,y)\ge0且\int_{-\infin}^{\infin}dx\int_{-\infin}^{\infin}f(x,y)dy=1 f(x,y)≥0且∫−∞∞dx∫−∞∞f(x,y)dy=1)
∫ − ∞ + ∞ f ( x , y ) d y = f X ( x ) \int_{-\infin}^{+\infin}f(x,y)dy=f_X(x) ∫−∞+∞f(x,y)dy=fX(x), X X X的边缘密度函数
∫ − ∞ + ∞ f ( x , y ) d x = f Y ( y ) \int_{-\infin}^{+\infin}f(x,y)dx=f_Y(y) ∫−∞+∞f(x,y)dx=fY(y), Y Y Y的边缘密度函数
二维连续型变量均匀分布
定义 D D D为 x o y xoy xoy面内有限区域,其面积为 A A A。若二维连续型随机变量 ( X , Y ) (X,Y) (X,Y)的联合密度为
f ( x , y ) = { 1 A , ( x , y ) ∈ D 0 , ( x , y ) ∉ D f(x,y)=\left\{ \begin{array}{l} \frac 1 A,(x,y)\in D \\0,(x,y)\notin D \end{array} \right. f(x,y)={A1,(x,y)∈D0,(x,y)∈/D
称 ( X , Y ) (X,Y) (X,Y)在 D D D上服从均匀分布,记 ( X , Y ) ∼ U ( D ) (X,Y)\sim U(D) (X,Y)∼U(D)
二维正太分布
设 ( X , Y ) (X,Y) (X,Y)为二维连续型随机变量,若 ( X , Y ) (X,Y) (X,Y)的联合密度函数为
f ( x , y ) = 1 2 π σ 1 σ 2 1 − ρ 2 e 1 − 2 ( 1 − ρ 2 ) [ ( x − μ 1 ) 2 σ 1 2 − 2 ρ x − μ 1 σ 1 y − μ 2 σ 2 + ( y − μ 2 ) 2 σ 2 2 ] f(x,y)=\frac 1 {2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}e^{\frac 1 {-2(1-\rho^2)}[\frac{(x-\mu_1)^2}{\sigma_1^2}-2\rho\frac{x-\mu_1}{\sigma_1}\frac{y-\mu_2}{\sigma_2}+\frac{(y-\mu_2)^2}{\sigma_2^2}]} f(x,y)=2πσ1σ21−ρ21e−2(1−ρ2)1[σ12(x−μ1)2−2ρσ1x−μ1σ2y−μ2+σ22(y−μ2)2]
称 ( X , Y ) (X,Y) (X,Y)服从以 μ 1 , μ 2 , σ 1 2 , σ 2 2 , ρ \mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho μ1,μ2,σ12,σ22,ρ为参数的二维正太分布,记 ( X , Y ) ∼ N ( μ 1 , μ 2 , σ 1 2 , σ 2 2 , ρ ) (X,Y)\sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho) (X,Y)∼N(μ1,μ2,σ12,σ22,ρ)
相关文章:

概率论:多维随机变量及分布
多维随机变量及分布 X X X为随机变量, ∀ x ∈ R , P { X ≤ x } F ( x ) \forall x\in R,P\{X\le x\}F(x) ∀x∈R,P{X≤x}F(x) 设 F ( x ) F(x) F(x)为 X X X的分布函数,则 (1) 0 ≤ F ( x ) ≤ 1 0\le F(x)\le1 0≤F(x)≤1 &am…...
flutter-第三方组件
卡片折叠 stacked_card_carousel 扫一扫组件 qr_code_scanner 权限处理组件 permission_handler 生成二维码组件 pretty_qr_code 角标组件 badges 动画组件 animations app更新 app_installer 带缓存的图片组件 cached_network_image 密码输入框 collection 图片保存 image_g…...
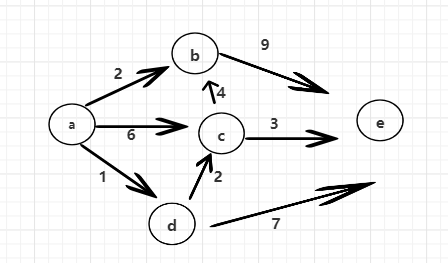
迪瑞克斯拉算法
迪锐克斯拉算法 简单来说就是在有向图中,给定一个图中具体的出发点,从这个点出发能够到达的所有的点,每个点的最短距离是多少。到不了的点,距离则是正无穷。有向,无负权重,可以有环。 所以说,迪…...
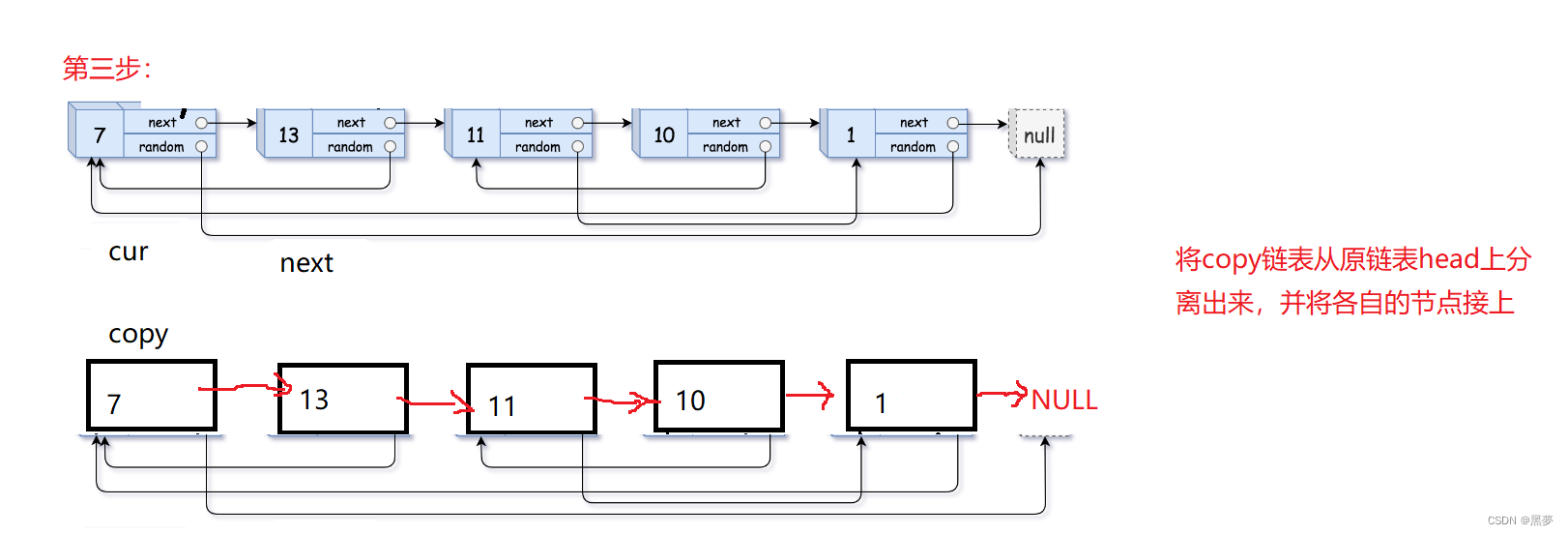
数据结构:力扣OJ题(每日一练)
目录 题一:环形链表 思路一: 题二:复制带随机指针的链表 思路一: 本人实力有限可能对一些地方解释的不够清晰,可以自己尝试读代码,望海涵! 题一:环形链表 给定一个链表的头节点…...

【论文阅读】基于深度学习的时序预测——Informer
系列文章链接 论文一:2020 Informer:长时序数据预测 论文二:2021 Autoformer:长序列数据预测 论文三:2022 FEDformer:长序列数据预测 论文四:2022 Non-Stationary Transformers:非平…...

机器学习 | Python实现GBDT梯度提升树模型设计
机器学习 | Python实现GBDT梯度提升树模型设计 目录 机器学习 | Python实现GBDT梯度提升树模型设计基本介绍模型描述模型使用参考资料基本介绍 机器学习 | Python实现GBDT梯度提升树模型设计。梯度提升树(Grandient Boosting)是提升树(Boosting Tree)的一种改进算法,GBDT也…...
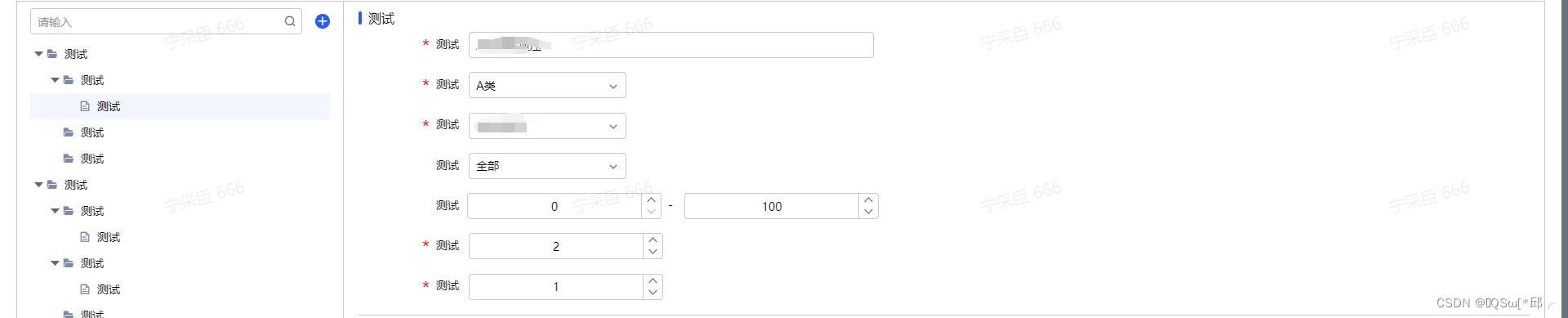
elementUi表单恢复至初始状态并不触发表单验证
elementUi表单恢复至初始状态并不触发表单验证 1.场景再现2.解决方法 1.场景再现 左侧是树形列表,右侧是显示节点的详情,点击按钮应该就是新增一个规则的意思,表单内容是没有改变的,所以就把需要把表单恢复至初始状态并不触发表单…...
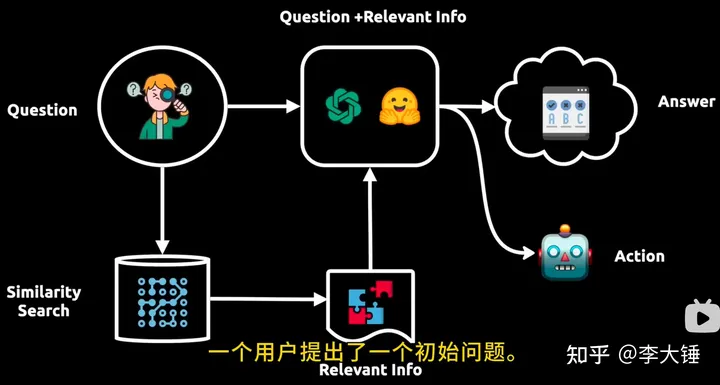
大模型相关知识
一. embedding 简单来说,embedding就是用一个低维的向量表示一个物体,可以是一个词,或是一个商品,或是一个电影等等。这个embedding向量的性质是能使距离相近的向量对应的物体有相近的含义,比如 Embedding(复仇者联盟)…...

无法在 macOS Ventura 上启动 Multipass
异常信息 ➜ ~ sudo multipass authenticate Please enter passphrase: authenticate failed: Passphrase is not set. Please multipass set local.passphrase with a trusted client. ➜ ~ multipass set local.passphrase Please enter passphrase: Please re-enter…...

算法通关村第六关——原来如此简单
层次遍历:又叫广度优先遍历。就是从根节点开始,先访问根节点下面一层全部元素,再访问之后的层次,直到访问完二叉树的最后一层。 我们先看一下基础的层次遍历题,力扣102题:给你一个二叉树,请你返…...
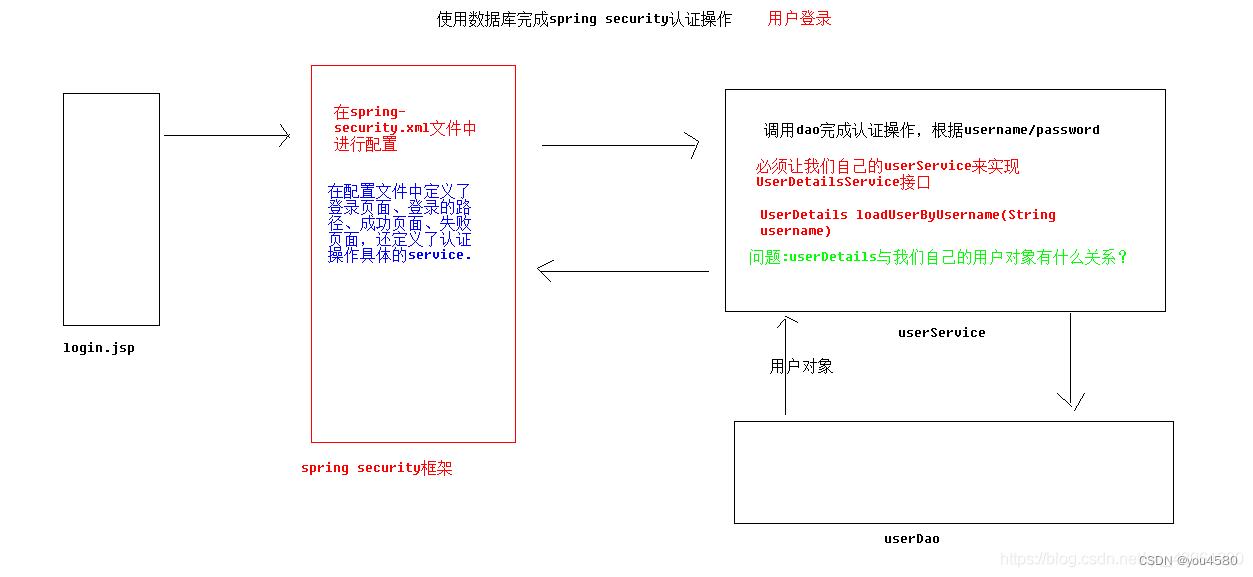
企业权限管理(八)-登陆使用数据库认证
Spring Security 使用数据库认证 在 Spring Security 中如果想要使用数据进行认证操作,有很多种操作方式,这里我们介绍使用 UserDetails 、 UserDetailsService来完成操作。 UserDetails public interface UserDetails extends Serializable { Collecti…...
第一百二十五天学习记录:C++提高:STL-deque容器(下)(黑马教学视频)
deque插入和删除 功能描述: 向deque容器中插入和删除数据 函数原型: 两端插入操作: push_back(elem); //在容器尾部添加一个数据 push_front(elem); //在容器头部插入一个数据 pop_back(); //删除容器最后一个数据 pop_front(); //删除容器…...

案例12 Spring MVC入门案例
网页输入http://localhost:8080/hello,浏览器展示“Hello Spring MVC”。 1. 创建项目 选择Maven快速构建web项目,项目名称为case12-springmvc01。 2.配置Maven依赖 <?xml version"1.0" encoding"UTF-8"?><project xm…...

【React】精选10题
1.React Hooks带来了什么便利? React Hooks是React16.8版本中引入的新特性,它带来了许多便利。 更简单的状态管理 使用useState Hook可以在函数组件中方便地管理状态,避免了使用类组件时需要继承React.Component的繁琐操作。 避免使用类组件…...

VS Spy++进程信息获取
查看进程中窗口信息。 Spy使用介绍 Windows下的程序及热键监视神器——Spy Word进程获取...
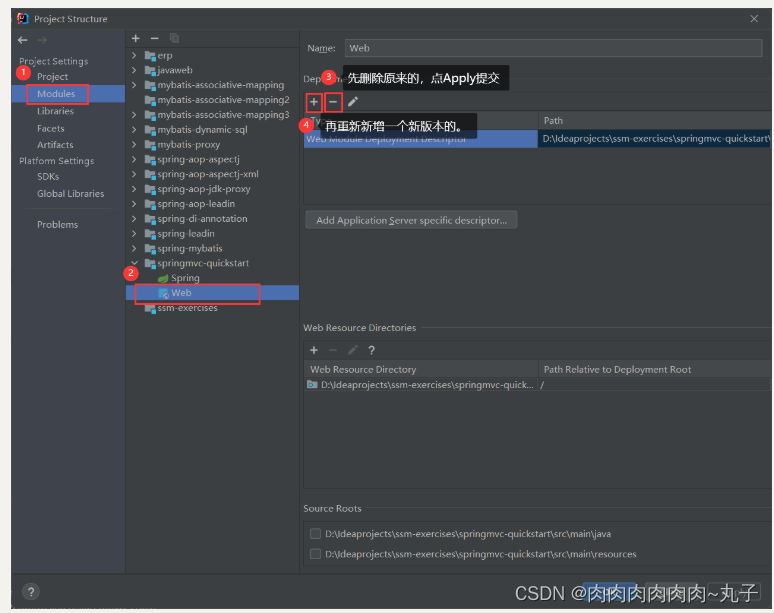
Java课题笔记~ SpringMVC概述
1.1 SpringMVC简介 SpringMVC 也叫Spring web mvc。是Spring 框架的一部分,在Spring3.0 后发布的。 1.2 SpringMVC的优点 基于MVC 架构 基于 MVC 架构,功能分工明确。解耦合。 容易理解,上手快,使用简单 就可以开发一个注解…...

SOPC之NIOS Ⅱ遇到的问题
记录NIOS Ⅱ中遇到的报错 一、NIOS II中Eclipse头文件未找到 问题:Unresolved inclusion: "system.h"等 原因:编译器无法找到头文件所在路径 解决方法: 在文件夹中找到要添加的头文件,并记录下其路径,如…...

uniapp uni-datetime-picker 日期和光标靠右
如果想在uni-datetime-picker组件中将日期和光标靠右,您可以使用自定义样式来实现。首先,您需要在页面的样式文件中定义一个类,用于定制uni-datetime-picker组件的样式。例如,你可以在App.vue或者页面的样式文件中添加以下代码&am…...

关于axios请求中的GET、POST、PUT、DELETE的一些认知
这篇写的特别好。而本文主要从实习用途中展开,不专业。 浅谈HTTP中Get、Post、Put与Delete的区别 1、Get 1、目前Get禁止使用requestBody形式传递值,如果使用了,后端会一直报错,让你确认是否有传递参数。 2、举例,模…...
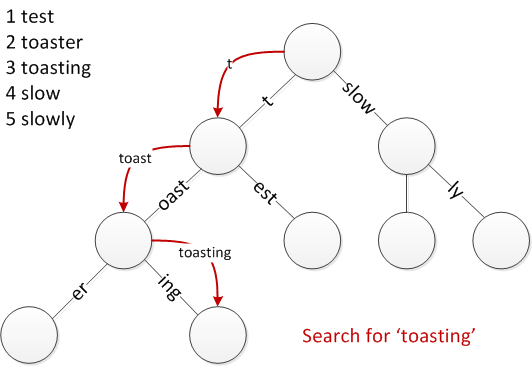
go-zero 是如何做路由管理的?
原文链接: go-zero 是如何做路由管理的? go-zero 是一个微服务框架,包含了 web 和 rpc 两大部分。 而对于 web 框架来说,路由管理是必不可少的一部分,那么本文就来探讨一下 go-zero 的路由管理是怎么做的,…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...
