解密人工智能:线性回归 | 逻辑回归 | SVM

文章目录
- 1、机器学习算法简介
- 1.1 机器学习算法包含的两个步骤
- 1.2 机器学习算法的分类
- 2、线性回归算法
- 2.1 线性回归的假设是什么?
- 2.2 如何确定线性回归模型的拟合优度?
- 2.3 如何处理线性回归中的异常值?
- 3、逻辑回归算法
- 3.1 什么是逻辑函数?
- 3.2 逻辑回归可以用于多类分类吗?
- 3.3 如何解释逻辑回归中的系数?
- 4、支持向量机(SVM)算法
- 4.1 优点
- 4.2 缺点
- 5、结语
1、机器学习算法简介
机器学习算法是一种基于数据和经验的算法,通过对大量数据的学习和分析,自动发现数据中的模式、规律和关联,并利用这些模式和规律来进行预测、分类或优化等任务。机器学习算法的目标是从数据中提取有用的信息和知识,并将其应用于新的未知数据中。

1.1 机器学习算法包含的两个步骤
机器学习算法通常包括两个主要步骤:训练和预测。在训练阶段,算法使用一部分已知数据(训练数据集)来学习模型或函数的参数,以使其能够对未知数据做出准确的预测或分类。在预测阶段,算法将学习到的模型应用于新的数据,通过模型对数据进行预测、分类或其他任务。
1.2 机器学习算法的分类
机器学习算法可以是基于统计学原理、优化方法、神经网络等等。根据学习的方式不同,机器学习算法可以分为监督学习、无监督学习和强化学习等几种类型。不同的机器学习算法适用于不同的问题和数据类型,选择合适的算法可以提高机器学习的任务效果。
-
监督学习算法:监督学习算法需要训练数据集中包含输入和对应的输出(或标签)信息。常用的监督学习算法包括:线性回归、逻辑回归、决策树、支持向量机、朴素贝叶斯、人工神经网络等。
-
无监督学习算法:无监督学习算法不需要训练数据集中的输出信息,主要用于数据的聚类和降维等问题。常用的无监督学习算法包括:K均值聚类、层次聚类、主成分分析、关联规则挖掘等。
-
强化学习算法:强化学习算法通过与环境进行交互,试图找到最优策略来最大化奖励。常用的强化学习算法包括:Q学习、深度强化学习算法等。
此外,还有一些常用的机器学习算法和技术,如集成学习、降维方法、深度学习、迁移学习、半监督学习等,它们通过不同的方式和建模方法来解决不同的问题。选择合适的机器学习算法需要考虑问题的性质、数据的特点、算法的可解释性和计算效率等因素。
2、线性回归算法
线性回归是一种统计方法,用于检查两个连续变量之间的关系:一个自变量和一个因变量。线性回归的目标是通过一组数据点找到最佳拟合线,然后可用于对未来的观察进行预测。

简单线性回归模型的方程为:
y = b 0 + b 1 ∗ x y = b0 + b1*x y=b0+b1∗x
其中 y 是因变量,x 是自变量,b0 是 y 截距(直线与 y 轴的交点),b1 是直线的斜率。斜率表示给定 x 变化时 y 的变化。
为了确定最佳拟合线,我们使用最小二乘法,该方法找到使预测 y 值与实际 y 值之间的平方差之和最小化的线。线性回归也可以扩展到多个自变量,称为多元线性回归。多元线性回归模型的方程为: y = b 0 + b 1 x 1 + b 2 x 2 + … + b n ∗ x n y = b0 + b1x1 + b2x2 + … + bn*xn y=b0+b1x1+b2x2+…+bn∗xn。其中 x1, x2, …, xn 是自变量,b1, b2, …, bn 是相应的系数。
线性回归可用于简单线性回归和多元线性回归问题。系数 b0 和 b1, …, bn 使用最小二乘法估计。一旦估计了系数,它们就可以用于对因变量进行预测。线性回归可用于对未来进行预测,例如预测股票的价格或将出售的产品的单位数量。然而,线性回归是一种相对简单的方法,可能并不适合所有问题。它假设自变量和因变量之间的关系是线性的,但情况可能并非总是如此。此外,线性回归对异常值高度敏感,这意味着如果存在任何不遵循数据总体趋势的极值,将会显着影响模型的准确性。
总之,线性回归是一种强大且广泛使用的统计方法,可用于检查两个连续变量之间的关系。它是一个简单但功能强大的工具,可用于预测未来。但是,请务必记住,线性回归假设变量之间存在线性关系,并且对异常值敏感,这可能会影响模型的准确性。
2.1 线性回归的假设是什么?
-
线性:自变量和因变量之间的关系是线性的。
-
独立性:观察结果彼此独立。
-
同方差性:误差项的方差在自变量的所有水平上都是恒定的。
-
正态性:误差项呈正态分布。
-
无多重共线性:自变量彼此不高度相关。
-
无自相关:误差项与其自身不自相关。
2.2 如何确定线性回归模型的拟合优度?
有多种方法可以确定线性回归模型的拟合优度:
-
R 平方:R 平方是一种统计度量,表示因变量中的方差由模型中的自变量解释的比例。R 平方值为 1 表示模型解释了因变量中的所有方差,值为 0 表示模型没有解释任何方差。
-
调整 R 平方:调整 R 平方是 R 平方的修改版本,它考虑了模型中自变量的数量。在比较具有不同数量自变量的模型时,它可以更好地指示模型的拟合优度。
-
均方根误差 (RMSE):RMSE 衡量预测值与实际值之间的差异。RMSE 较低表明模型与数据的拟合效果更好。
-
平均绝对误差 (MAE):MAE 测量预测值与实际值之间的平均差异。MAE 越低表明模型与数据的拟合效果越好。

2.3 如何处理线性回归中的异常值?
线性回归中的异常值可能会对模型的预测产生重大影响,因为它们可能会扭曲回归线。处理线性回归中的异常值有多种方法,包括以下几点:
-
删除异常值:一种选择是在训练模型之前简单地从数据集中删除异常值。然而,这可能会导致重要信息的丢失。
-
转换数据:应用转换(例如记录数据日志)有助于减少异常值的影响。
-
使用稳健回归方法:稳健回归方法(例如 RANSAC 或 Theil-Sen)对异常值的敏感度低于传统线性回归。
-
使用正则化:正则化可以通过在成本函数中添加惩罚项来帮助防止由异常值引起的过度拟合。
总之,采用什么方法将取决于特定的数据集和分析的目标。
3、逻辑回归算法
逻辑回归是一种统计方法,用于根据一个或多个自变量预测二元结果,例如成功或失败。它是机器学习中的一种流行技术,通常用于分类任务,例如确定电子邮件是否是垃圾邮件,或预测客户是否会流失。

逻辑回归模型基于逻辑函数,逻辑函数是一个sigmoid函数,它将输入变量映射到 0 到 1 之间的概率。然后使用该概率对结果进行预测。
逻辑回归模型由以下方程表示:
P ( y = 1 ∣ x ) = 1 / ( 1 + e − ( b 0 + b 1 x 1 + b 2 x 2 + … + b n ∗ x n ) ) P(y=1|x) = 1/(1+e^-(b0 + b1x1 + b2x2 + … + bn*xn)) P(y=1∣x)=1/(1+e−(b0+b1x1+b2x2+…+bn∗xn))
其中 P(y=1|x) 是给定输入变量 x 时结果 y 为 1 的概率,b0 是截距,b1, b2, …, bn 是输入变量 x1, x2, … 的系数, xn。通过在数据集上训练模型并使用优化算法(例如梯度下降)来最小化成本函数(通常是对数损失)来确定系数。模型训练完成后,就可以通过输入新数据并计算结果为 1 的概率来进行预测。将结果分类为 1 或 0 的阈值通常设置为 0.5,但这可以根据情况进行调整具体任务以及误报和漏报之间所需的权衡。
3.1 什么是逻辑函数?
逻辑函数,也称为 s i g m o i d sigmoid sigmoid函数,是一条 S 形曲线,将任何实数值映射到 0 到 1 之间的值。它的定义为 f ( x ) = 1 / ( 1 + e − x ) f(x) = 1 / (1 + e^-x ) f(x)=1/(1+e−x)其中 e 是自然对数的底。逻辑函数在逻辑回归中用于对二元结果的概率进行建模。

3.2 逻辑回归可以用于多类分类吗?
逻辑回归可用于多类分类,方法是为每个类创建单独的二元逻辑回归模型并选择预测概率最高的类。这被称为一对一或一对一的方法。或者,我们可以使用 s o f t m a x softmax softmax回归,它是逻辑回归的推广,可以直接处理多个类。
3.3 如何解释逻辑回归中的系数?
逻辑回归中的系数表示在保持所有其他预测变量不变的情况下,预测变量发生一个单位变化时结果的对数几率的变化。优势比可用于解释系数的大小。优势比大于 1 表示预测变量增加一个单位会增加结果的可能性,而优势比小于 1 表示预测变量增加一个单位会降低结果的可能性。
4、支持向量机(SVM)算法
支持向量机 (SVM) 是一种监督学习算法,可用于分类或回归问题。SVM 背后的主要思想是通过最大化间隔(边界与每个类最近的数据点之间的距离)来找到分隔数据中不同类的边界。这些最接近的数据点称为支持向量。

当数据不可线性分离(这意味着数据不能用直线分离)时,SVM 特别有用。在这些情况下,SVM 可以使用称为核技巧的技术将数据转换为更高维的空间,其中可以找到非线性边界。SVM 中使用的一些常见核函数包括多项式、径向基函数 (RBF) 和 s i g m o i d sigmoid sigmoid。
SVM 的主要优点之一是它们在高维空间中非常有效,并且即使在特征数量大于样本数量时也具有良好的性能。此外,SVM 内存效率高,因为它们只需要存储支持向量,而不是整个数据集。另一方面,SVM 对核函数和算法参数的选择很敏感。还需要注意的是,SVM 不适合大型数据集,因为训练时间可能相当长。总之,支持向量机(SVM)是一种强大的监督学习算法,可用于分类和回归问题,特别是当数据不可线性分离时。该算法以其在高维空间中的良好性能以及发现非线性边界的能力而闻名。然而,它对核函数和参数的选择很敏感,也不适合大型数据集。
4.1 优点
-
在高维空间中有效:即使当特征数量大于样本数量时,SVM 也具有良好的性能。
-
内存效率高:SVM 只需要存储支持向量,而不需要存储整个数据集,因此内存效率高。
-
通用性:SVM 可用于分类和回归问题,并且可以使用核技巧处理非线性可分离数据。
-
对噪声和异常值具有鲁棒性:SVM 对数据中的噪声和异常值具有鲁棒性,因为它们仅依赖于支持向量。
4.2 缺点
-
对核函数和参数的选择敏感:SVM 的性能高度依赖于核函数的选择和算法参数。
-
不适合大型数据集:对于大型数据集,SVM 的训练时间可能会相当长。
-
解释结果困难:解释 SVM 的结果可能很困难,特别是在使用非线性核时。
-
不适用于重叠类:当类有明显重叠时,SVM 可能会遇到困难。
总之,SVM 是一种强大且通用的机器学习算法,可用于分类和回归问题,特别是当数据不可线性分离时。然而,它们可能对核函数和参数的选择敏感,不适合大型数据集,并且难以解释结果。
5、结语
今天的分享到这里就结束啦!如果觉得文章还不错的话,可以三连支持一下,春人的主页还有很多有趣的文章,欢迎小伙伴们前去点评,您的支持就是春人前进的动力!

相关文章:

解密人工智能:线性回归 | 逻辑回归 | SVM
文章目录 1、机器学习算法简介1.1 机器学习算法包含的两个步骤1.2 机器学习算法的分类 2、线性回归算法2.1 线性回归的假设是什么?2.2 如何确定线性回归模型的拟合优度?2.3 如何处理线性回归中的异常值? 3、逻辑回归算法3.1 什么是逻辑函数?…...

【FFMPEG应用篇】使用FFmpeg的常见问题
拼接视频的问题 在使用ffmpeg进行视频拼接时,可能会遇到一些常见问题。以下是这些问题及其解决方法: 1. 视频格式不兼容:如果要拼接的视频格式不同,ffmpeg可能会报错。解决方法是使用ffmpeg进行格式转换,将所有视频转…...
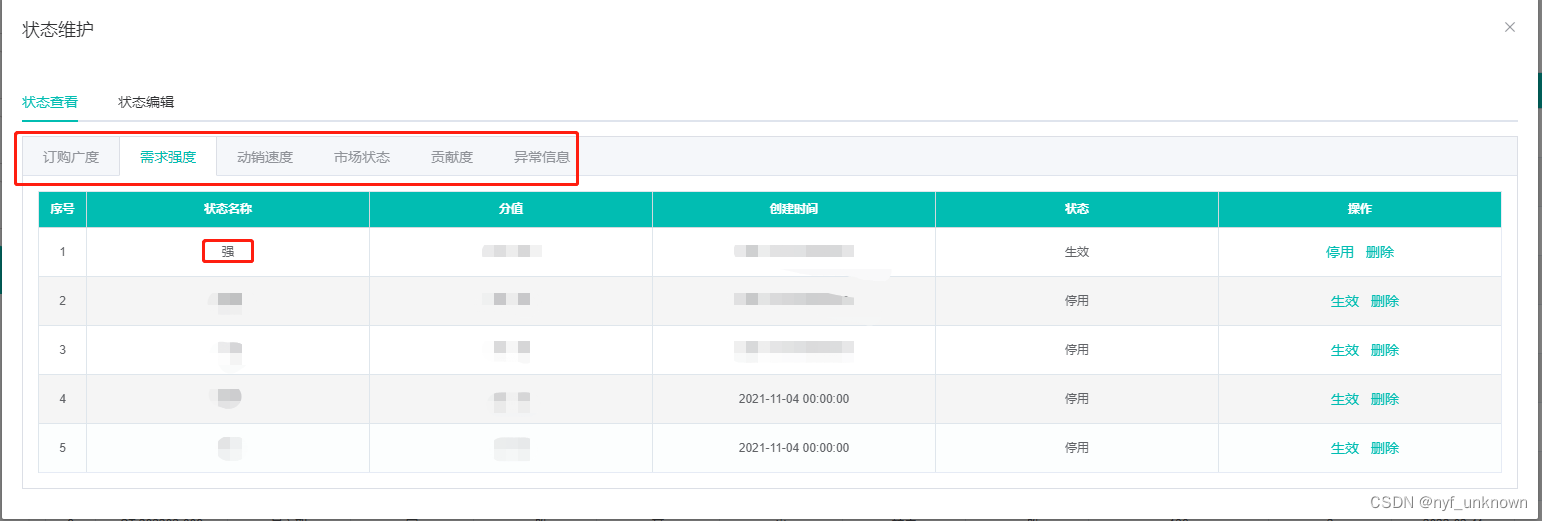
(vue)获取对象的键遍历,同时循环el-tab页展示key及内容
(vue)获取对象的键遍历,同时循环el-tab页展示key及内容 效果: 数据结构: "statusData": {"订购广度": [ {"id": 11, "ztName": "广", …...

【严重】Smartbi未授权设置Token回调地址获取管理员权限
漏洞描述 Smartbi是一款商业智能应用,提供了数据集成、分析、可视化等功能,帮助用户理解和使用他们的数据进行决策。 在 Smartbi 受影响版本中存在Token回调地址漏洞,未授权的攻击者可以通过向目标系统发送POST请求/smartbix/api/monitor/s…...

北京鸟巢门票多少,里面有什么好玩的
北京鸟巢门票多少,里面有什么好玩的 北京鸟巢的门票是100元,里面有很多运动设施,“鸟巢”结构设计奇特新颖,而这次搭建它的钢结构的Q460也有很多独到之处:Q460是一种低合金高强度钢,它在受力强度达到460兆帕…...
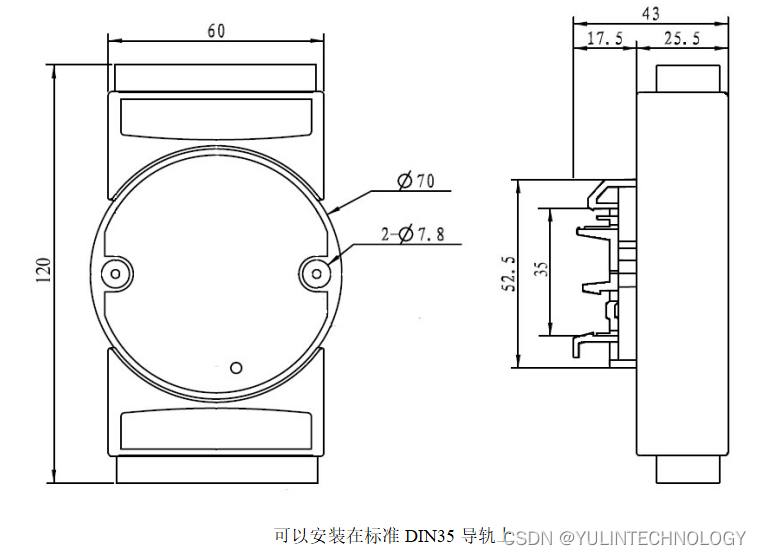
4路光栅尺磁栅尺编码器5MHz高速差分信号转Modbus TCP网络模块 YL97
特点: ● 光栅尺磁栅尺解码转换成标准Modbus TCP协议 ● 光栅尺5V差分信号直接输入,4倍频计数 ● 模块可以输出5V的电源给光栅尺供电 ● 高速光栅尺磁栅尺计数,频率可达5MHz ● 支持4个光栅尺同时计数,可识别正反转 ● 可网…...

金蝶云星空对接打通旺店通·企业奇门组装拆卸单查询接口与创建其他出库单接口
金蝶云星空对接打通旺店通企业奇门组装拆卸单查询接口与创建其他出库单接口 编辑 源系统:金蝶云星空 金蝶K/3Cloud(金蝶云星空)是移动互联网时代的新型ERP,是基于WEB2.0与云技术的新时代企业管理服务平台。金蝶K/3Cloud围绕着“生态、人人…...

卫星--夏令营
几何问题:就是用几何数学知识解题即可 但是越是数学编程题,越容易忽略数学题中的细节 1.地球半径你算进去了吗? 2.sin三角函数,M_PI标准圆周率在cmath文件里 3.有可能给出的夹角超过180呢,没给数据要求,就要自己考…...
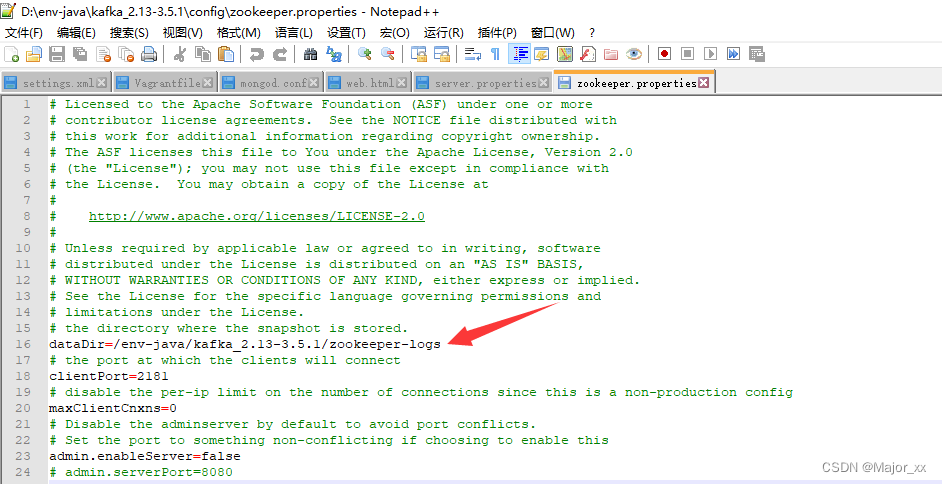
Kafka的下载安装以及使用
一、Kafka下载 下载地址:https://kafka.apache.org/downloads 二、Kafka安装 因为选择下载的是 .zip 文件,直接跳过安装,一步到位。 选择在任一磁盘创建空文件夹(不要使用中文路径),解压之后把文件夹内容…...
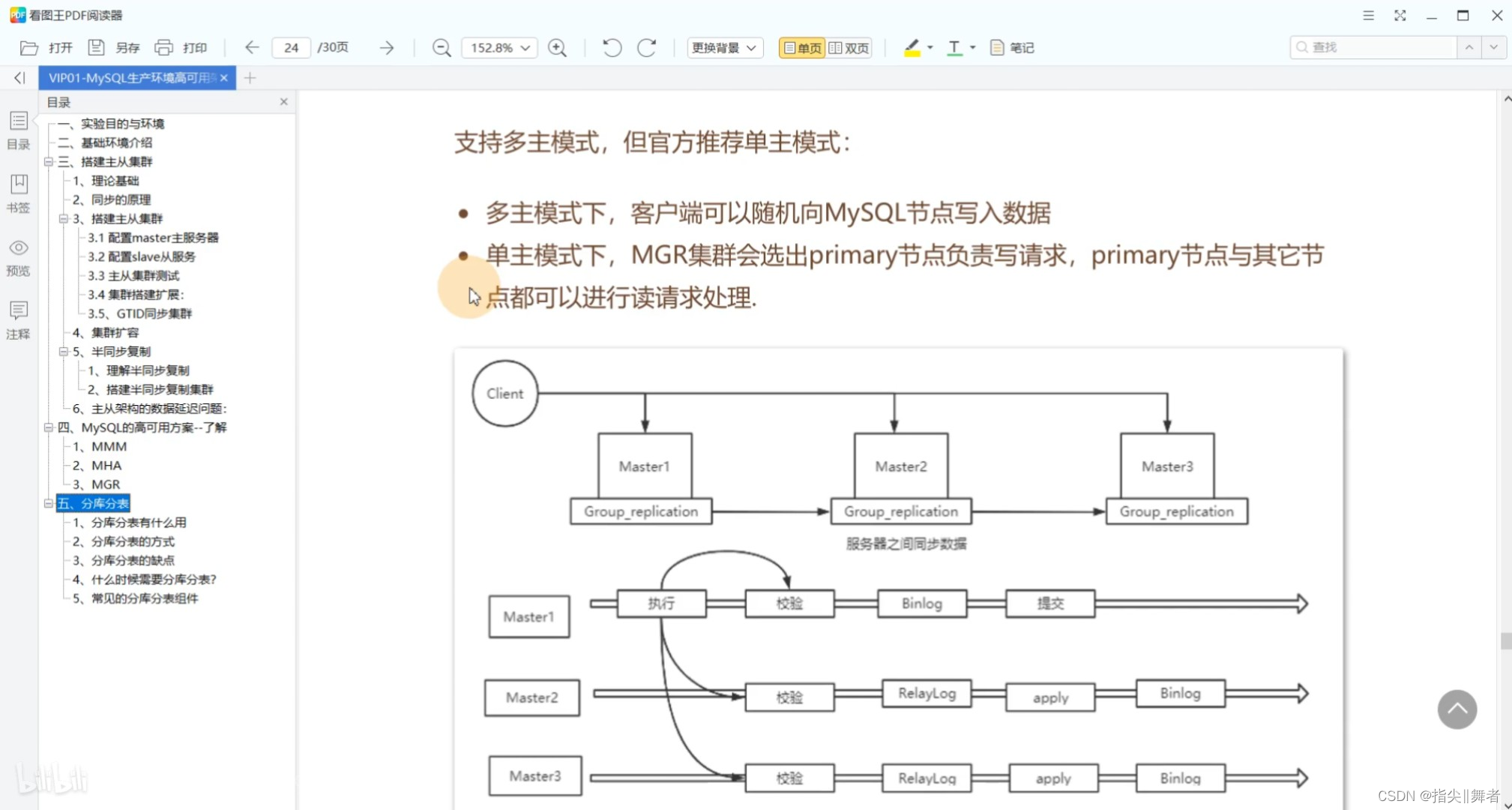
数据库相关面试题
巩固基础,砥砺前行 。 只有不断重复,才能做到超越自己。 能坚持把简单的事情做到极致,也是不容易的。 mysql怎么优化 : MySQL的优化可以从以下几个方面入手: 数据库设计优化:合理设计表结构,选择合适的数…...
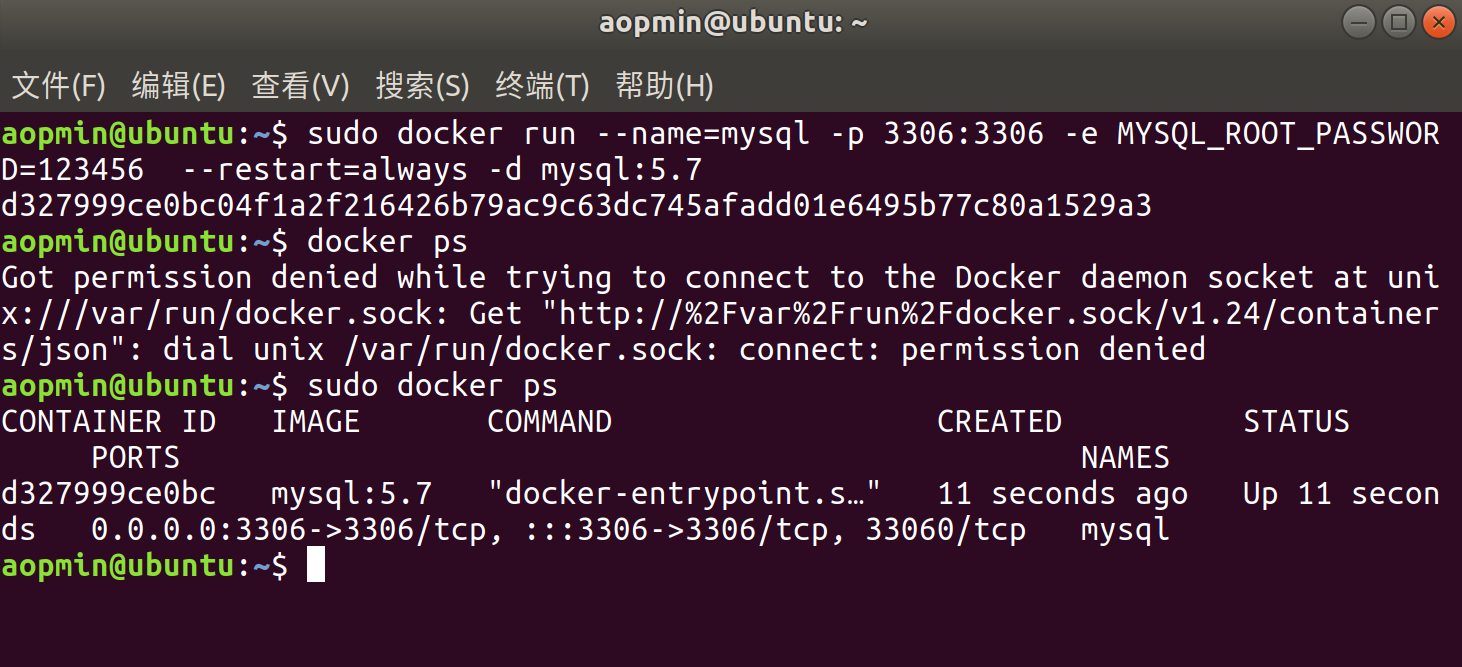
Ubuntu常用配置
文章目录 1. 安装VMware虚拟机软件2. 下载Ubuntu镜像3. 创建Ubuntu虚拟机4. 设置屏幕分辨率5. 更改系统语言为中文6. 切换中文输入法7. 修改系统时间8. 修改锁屏时间9. 通过系统自带的应用商店安装软件10. 安装JDK11. 安装 IntelliJ IDEA12. 将左侧任务栏自动隐藏13. 安装docke…...

win10MySQLServer安装过程+解决MySQL服务无法启动问题
本次使用的版本是 Server version: 8.0.33 MySQL Community Server 安装详解 首先去官网下载社区版,比如我用的是mysql-8.0.33-winx64.zip,解压到文件夹:D:\Program Files\mysql-8.0.33-winx64 用管理员身份运行cmd,进到bin目录…...
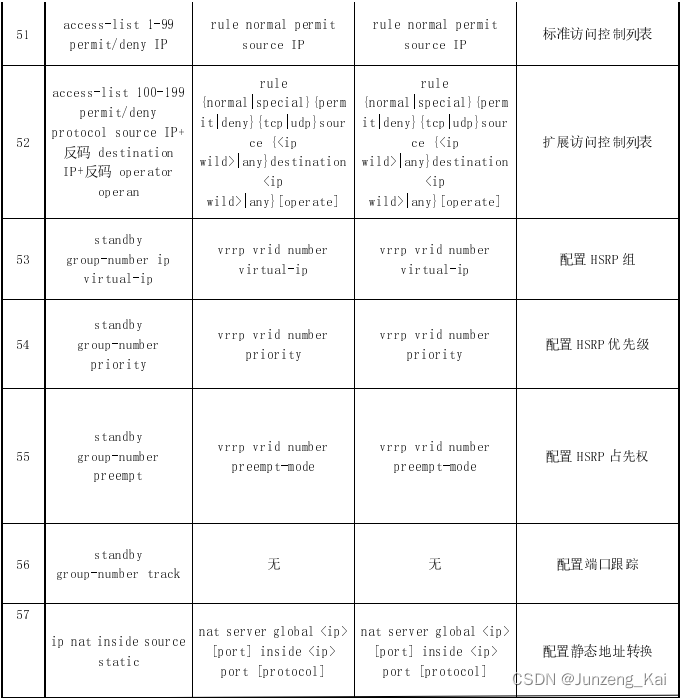
网络:CISCO、Huawei、H3C命令对照
思科、华为、锐捷命令对照表 编号思科华为锐捷命令解释1 2writesavesave保存3456 如果你所处的视图为非系统视图,需要查看配置的时候,需要在该配置命令前加do。 在特定的视图之下,有对应的特定命令。例如,在接口视图下的ip addre…...

题目:2319.判断矩阵是否是 X 矩阵
题目来源: leetcode题目,网址:2319. 判断矩阵是否是一个 X 矩阵 - 力扣(LeetCode) 解题思路: 遍历矩阵,对于每一个节点,先判断是否处于主对角线或副对角线上,然后判…...

2023年大厂前端面试题汇总
一、58同城前端面试题27道 1. css盒模型 2. css画三角形 3. 盒子水平垂直居中(所有方式) 4. 重绘、重排 重绘就是重新绘制(repaint):是在一个元素的外观被改变所触发的浏览器行为,浏览器会根据元素的新属性…...

如何在Linux中查找Nginx安装目录
一、通过which命令查找 $ which nginx /usr/sbin/nginxwhich命令会在系统环境变量PATH中查找nginx可执行文件,并返回路径。因此,通过which命令可以很容易地找到系统中nginx的安装位置。 二、通过whereis命令查找 $ whereis nginx nginx: /usr/sbin/ng…...

【NLP】训练LLM的不同方式
一、说明 在大型语言模型(LLM)领域,有各种各样的 训练机制,具有不同的手段,要求和目标。由于它们服务于不同的目的,因此重要的是不要将它们相互混淆,并了解它们适用的不同场景。 在本文中&#…...
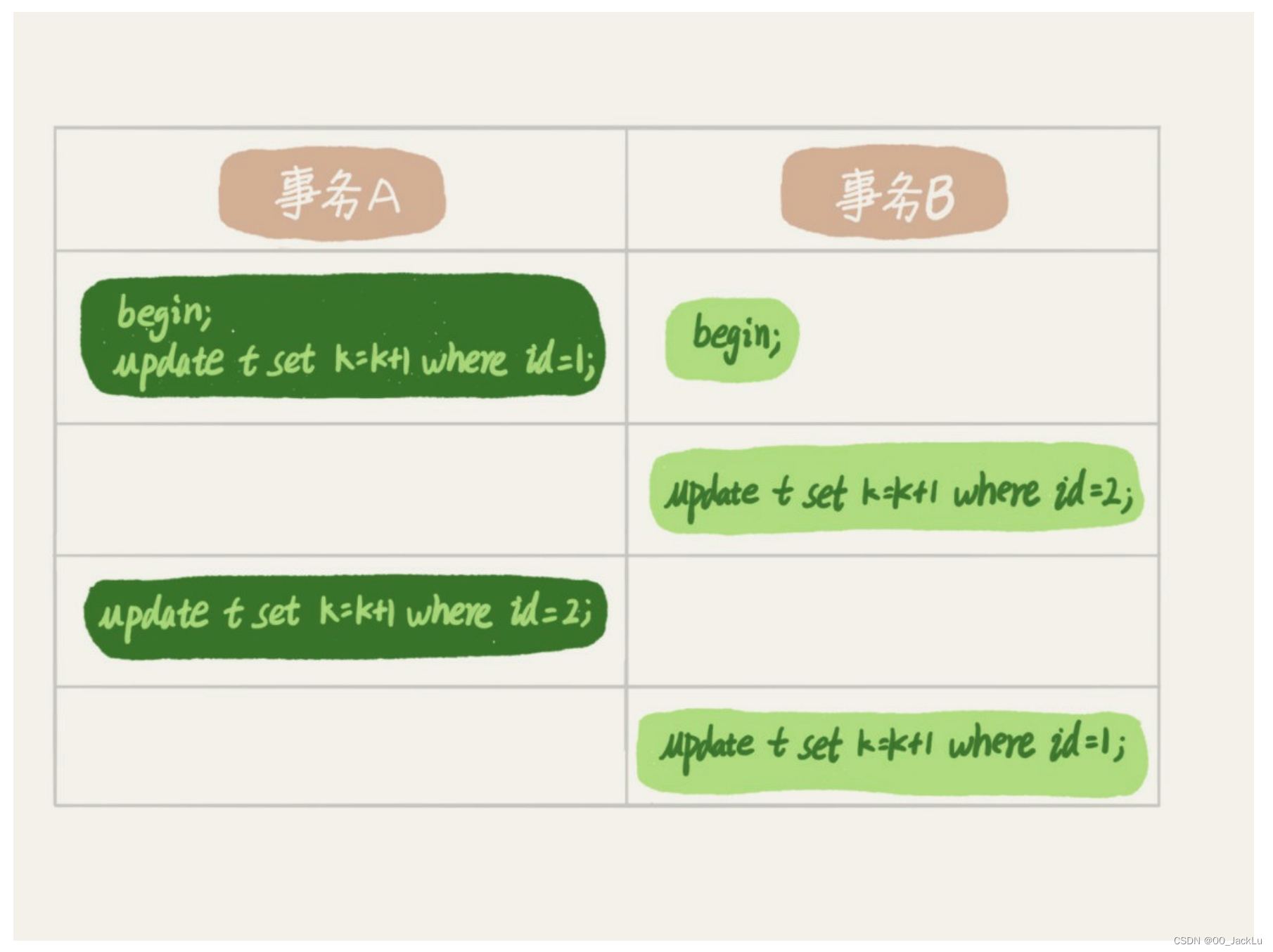
MySQL 45讲笔记(1-10讲)
1. SQL语句如何开始执行? MySQL分为Server和存储引擎两部分: Server层包含连接器、存储缓存、分析器、执行器等,以及所有的内置函数(事件、日期)等等,还有视图、触发器。 存储引擎是负责数据的存储和提取&a…...
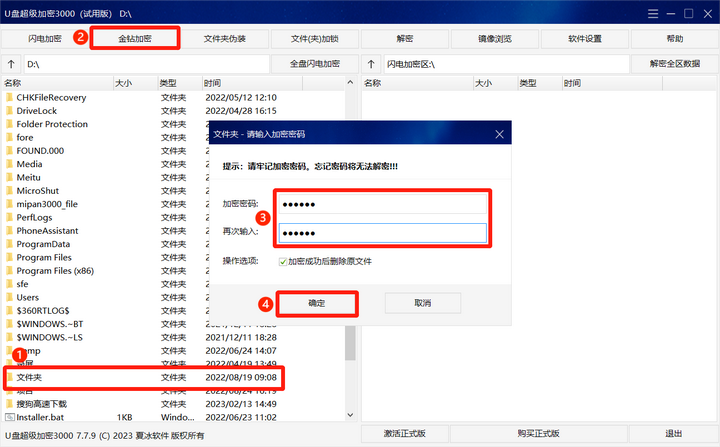
U盘数据如何保密?U盘数据加密软件合集
当我们将重要数据存放在U盘中时,必须要保障U盘的安全,以避免数据泄露。那么,U盘数据该如何保密呢?下面我们就来盘点一下那些好用的U盘数据保护方法。 U盘写保护 起初U盘写保护是专门为U盘防病毒而设计的,写保护后会将…...
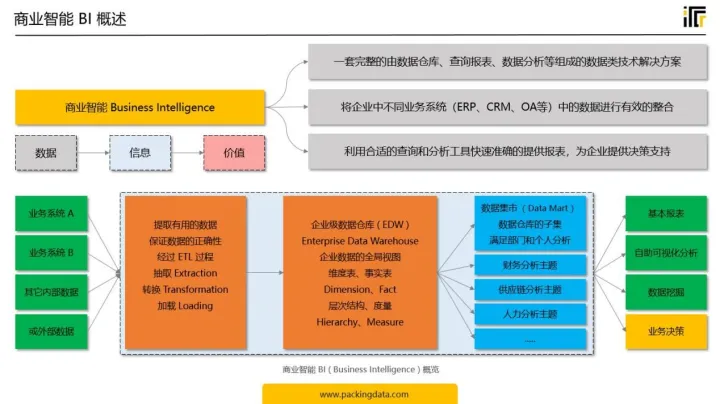
此文详解,数据仓库管理建设的经验
目前由于数据分散在不同的存储环境或数据库中,对于新业务需求的开发需要人工先从不同的数据库中同步、集中、合并等处理,造成资源和人力的浪费。同时,目前的系统架构,无法为未来数据驱动业务创新的理念提供友好的支撑。需要建设新…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
