[保研/考研机试] KY103 2的幂次方 上海交通大学复试上机题 C++实现
题目链接:
KY103 2的幂次方 ![]() https://www.nowcoder.com/share/jump/437195121691999575955
https://www.nowcoder.com/share/jump/437195121691999575955
描述
Every positive number can be presented by the exponential form.For example, 137 = 2^7 + 2^3 + 2^0。 Let's present a^b by the form a(b).Then 137 is presented by 2(7)+2(3)+2(0). Since 7 = 2^2 + 2 + 2^0 and 3 = 2 + 2^0 , 137 is finally presented by 2(2(2)+2 +2(0))+2(2+2(0))+2(0). Given a positive number n,your task is to present n with the exponential form which only contains the digits 0 and 2.
输入描述:
For each case, the input file contains a positive integer n (n<=20000).
输出描述:
For each case, you should output the exponential form of n an a single line.Note that,there should not be any additional white spaces in the line.
中文描述:
每个正数都可以用指数形式表示。例如,137 = 2^7 + 2^3 + 2^0。我们用a(b)的形式表示a^b。那么137可以用2(7)表示 +2(3)+2(0)。 由于 7 = 2^2 + 2 + 2^0 和 3 = 2 + 2^0 ,因此 137 最终由 2(2(2)+2 +2(0))+2(2+2(0)) 表示 +2(0)。 给定一个正数 n,你的任务是将 n 以仅包含数字 0 和 2 的指数形式呈现。
输入描述:
对于每种情况,输入文件都包含一个正整数 n (n<=20000)。
输出描述:
对于每种情况,您应该在一行中输出 n 的指数形式。请注意,该行中不应有任何额外的空格。
示例1
输入:
1315输出:
2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)思路:
-
首先,定义一个递归函数 powTwo,将数字 n 转换为二进制形式,其中只有 0 和 1。
-
在递归函数中,处理二进制数,如果某一位为 1,则根据指数规则,将其转换为对应的 2(a) 形式。
-
注意处理特殊情况,例如 2^1 直接表示为 "+2",其他情况通过递归处理更高次幂。
-
最后,去掉字符串开头的 "+" 符号,即为所求的指数形式表示。
-
在 main 函数中,读入输入的正整数 n,并调用递归函数 powTwo 输出结果。
源代码:
#include <iostream>
#include <vector>
using namespace std;// 定义递归函数,将数字 n 转换为指数形式
string powTwo(int n) {if (n == 0) {return "0";}if (n == 2) {return "2";}vector<int> nums;while (n != 0) {nums.push_back(n % 2); // 将 n 转换为二进制n /= 2;}string res = "";for (int i = nums.size() - 1; i >= 0; i--) {if (nums[i] == 1) {if (i == 1) {res += "+2"; // 如果是 2^1,直接添加 "+2"}else {res += "+2(" + powTwo(i) + ")"; // 否则递归处理更高次幂}}}res.erase(0, 1); // 去掉最前面的 "+"return res;
}int main() {int n;while (cin >> n) {cout << powTwo(n) << endl;}return 0;
}
提交结果:
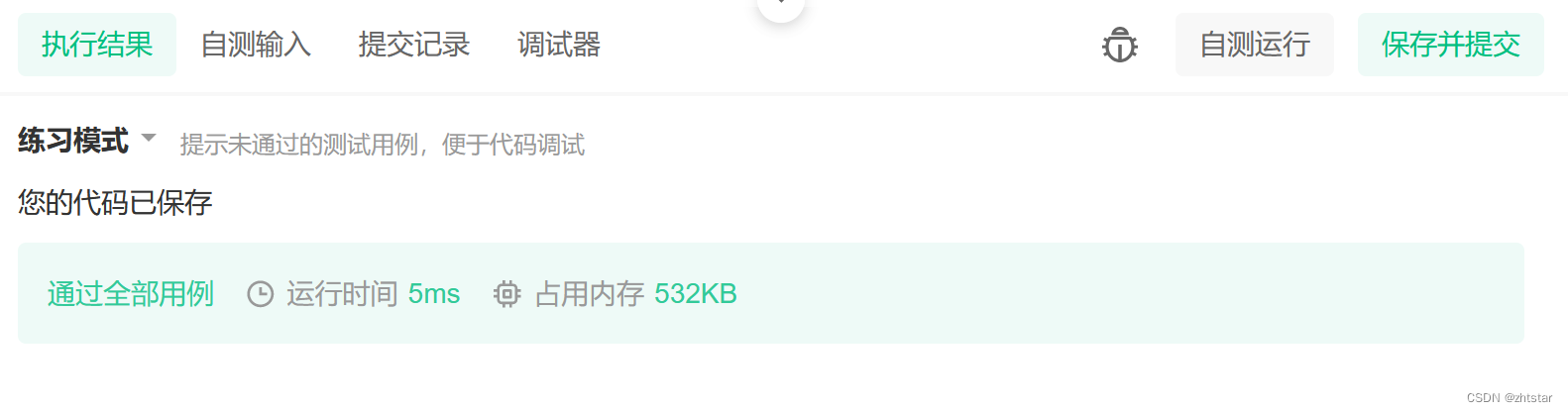
相关文章:

[保研/考研机试] KY103 2的幂次方 上海交通大学复试上机题 C++实现
题目链接: KY103 2的幂次方 https://www.nowcoder.com/share/jump/437195121691999575955 描述 Every positive number can be presented by the exponential form.For example, 137 2^7 2^3 2^0。 Lets present a^b by the form a(b).Then 137 is present…...

时序预测 | MATLAB实现基于BP神经网络的时间序列预测-递归预测未来(多指标评价)
时序预测 | MATLAB实现基于BP神经网络的时间序列预测-递归预测未来(多指标评价) 目录 时序预测 | MATLAB实现基于BP神经网络的时间序列预测-递归预测未来(多指标评价)预测结果基本介绍程序设计参考资料 预测结果 基本介绍 Matlab实现BP神经网络时间序列预测未来(完整…...

组合模式(C++)
定义 将对象组合成树形结构以表示部分-整体’的层次结构。Composite使得用户对单个对象和组合对象的使用具有一致性(稳定)。 应用场景 在软件在某些情况下,客户代码过多地依赖于对象容器复杂的内部实现结构,对象容器内部实现结构(而非抽象接口)的变化…...

git上传问题记录
unable to access ‘https://github.com/songjiahao-wq/untitled.git/’: Failed to connect to github.com port 443 after 21086 ms: Couldn’t connect to serve 解决办法:修改 Git 的网络设置 打开git Bash运行,clash代理一般是下面的端口 # 注意…...

通过动态IP解决网络数据采集问题
动态地址的作用 说到Python网络爬虫,很多人都会遇到困难。最常见的就是爬取过程中IP地址被屏蔽。虽然大部分都是几个小时内自动解封的,但这对于分秒必争的python网络爬虫来说,是一个关键性的打击!当一个爬虫被阻塞时,…...

可重入锁,不可重入锁,死锁的多种情况,以及产生的原因,如何解决,synchronized采用的锁策略(渣女圣经)自适应的底层,锁清除,锁粗化,CAS的部分应用
一、💛 锁策略——接上一篇 6.分为可重入锁,不可重入锁 如果一个线程,针对一把锁,连续加锁两次,会出现死锁,就是不可重入锁,不会出现死锁,就是可重入锁。 如果一个线程,针…...
和JSON.stringify()用法)
JSON.parse()和JSON.stringify()用法
JSON.parse() 方法用于将 JSON 格式的字符串转换为 JavaScript 对象,而 JSON.stringify() 方法用于将 JavaScript 对象转换为 JSON 字符串。这两个方法可以组合使用来实现将数据从对象到字符串再到对象的转换。 示例 // 创建一个包含属性的 JavaScript 对象 var pe…...
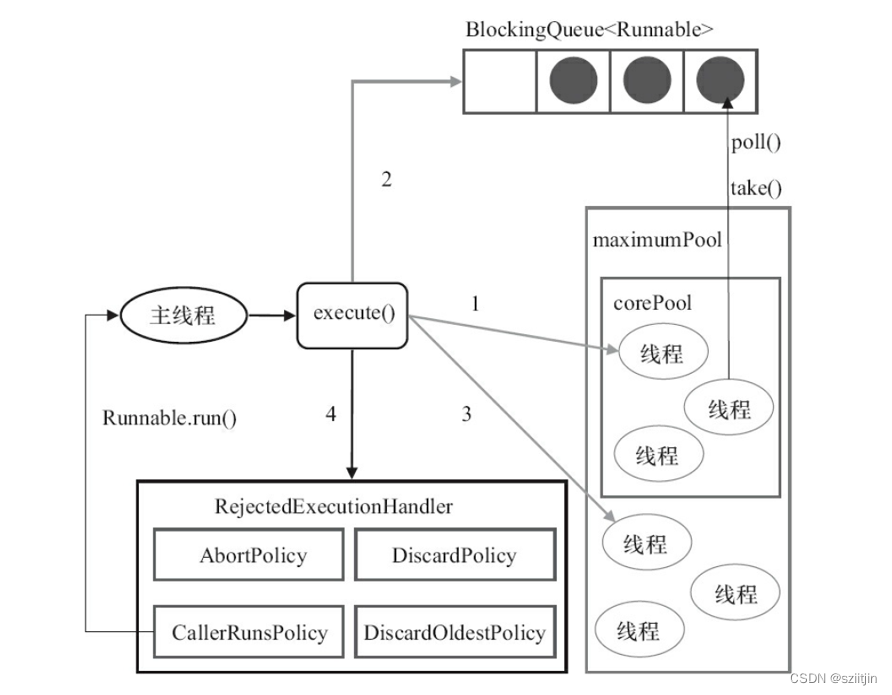
Android 并发编程--阻塞队列和线程池
一、阻塞队列 队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作…...

Playwright快速上手-1
前言 随着近年来对UI自动化测试的要求越来越高,,功能强大的测试框架也不断的涌现。本系列主讲的Playwright作为一款新兴的端到端测试框架,凭借其独特优势,正在逐渐成为测试工程师的热门选择。 本系列文章将着重通过示例讲解 Playwright python开发环境的搭建 …...
PPT颜色又丑又乱怎么办?
一、设计一套PPT时,可以从这5个方面进行设计 二、PPT颜色 (一)、PPT常用颜色分类 一个ppt需要主色、辅助色、字体色、背景色即可。 (二)、搭建PPT色彩系统 设计ppt时,根据如下几个步骤,依次选…...

python计算相关系数R
方法一: import numpy as np# 计算相关系数R def r(y_true, y_pred):y_true np.array(y_true)y_pred np.array(y_pred)corr np.corrcoef(y_true, y_pred)[0][1]return corrcorr r(yture, ypred)方法二 import scipy.stats # 计算皮尔逊相关指数,并…...

黑马项目一阶段面试 自我介绍篇
面试官你好,我叫xxx,是来自xxxx的本科毕业生。我通过招聘网站/内推/线下招聘了解到的贵司,我具有扎实的Java后端的基础功底,基本掌握JavaSE、JavaEE流行技术的使用,并且我比较好学,心态也很乐观积极&#x…...

时序预测 | MATLAB实现CNN-BiGRU-Attention时间序列预测
时序预测 | MATLAB实现CNN-BiGRU-Attention时间序列预测 目录 时序预测 | MATLAB实现CNN-BiGRU-Attention时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 MATLAB实现CNN-BiGRU-Attention时间序列预测,CNN-BiGRU-Attention结合注意力机制时…...
开发过程中遇到的问题以及解决方法
巩固基础,砥砺前行 。 只有不断重复,才能做到超越自己。 能坚持把简单的事情做到极致,也是不容易的。 开发过程中遇到的问题以及解决方法 简单易用的git命令 git命令: 查看有几个分支:git branch -a 切换分支&#…...
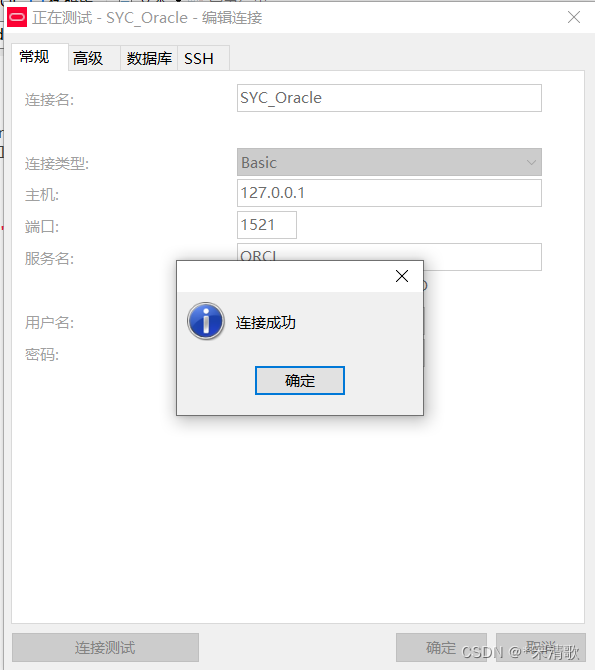
本地oracle登录账号锁定处理,the account is locked
1.打开cmd命令窗口 2.打开sqlplus: sqlplus /nolog(加/nolog是不登录服务器的意思,不加就需要输账号密码) 3.切换到管理员:conn / as sysdba; 第2步第3步可以合并,直接使用sysdba登录:sqlplus / as sysdba; 4.解锁账号&#x…...

redission自定义hessian序列化
一。技术改造背景 由于之前的比较陈旧的技术,后面发起了技术改造,redis整体改后使用redisson框架。 二。问题 改造完成后,使用方反馈 缓存获取异常 异常信息如下 Caused by: java.io.CharConversionException: Unexpected EOF in the mid…...
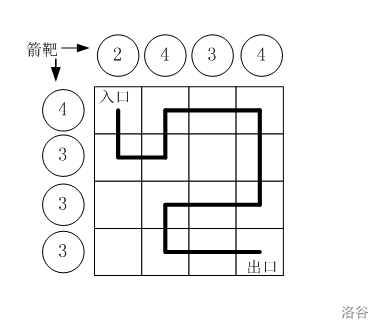
P8642 [蓝桥杯 2016 国 AC] 路径之谜
[蓝桥杯 2016 国 AC] 路径之谜 题目描述 小明冒充 X X X 星球的骑士,进入了一个奇怪的城堡。 城堡里边什么都没有,只有方形石头铺成的地面。 假设城堡地面是 n n n\times n nn 个方格。如图所示。 按习俗,骑士要从西北角走到东南角。 …...
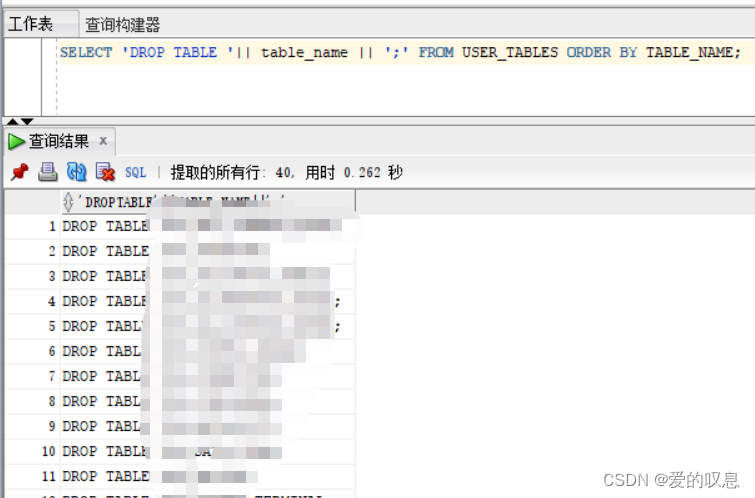
oracle sql developer批量删除某个用户
随着navicate收费,还得破解,pl/sql developer配置麻烦,最近使用oracle sql developer来试试oracle的操作如何; 用着还行,没有卡顿现象, 最近要oracle sql developer批量删除某个用户下所有的表࿰…...
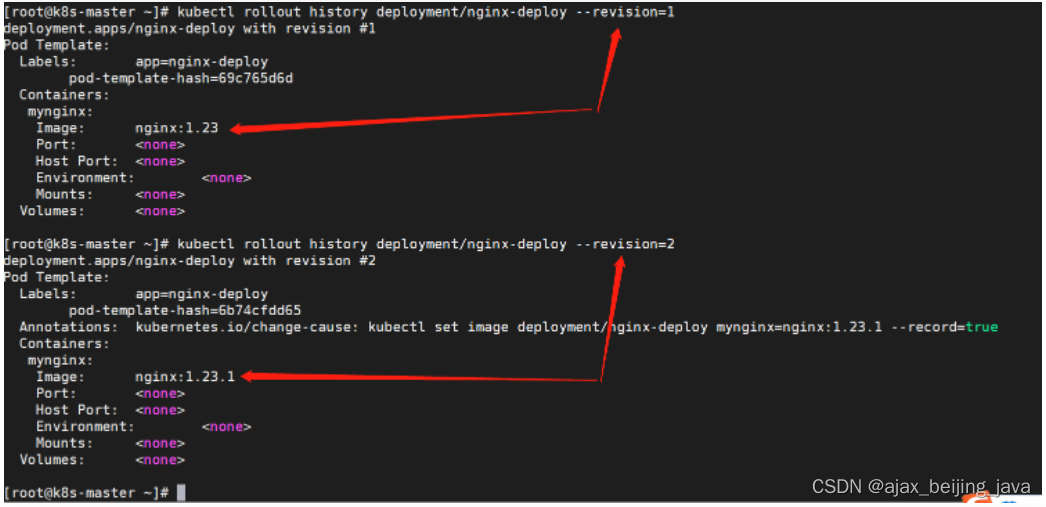
k8s 滚动更新控制(一)
在传统的应用升级时,通常采用的方式是先停止服务,然后升级部署,最后将新应用启动。这个过程面临一个问题,就是在某段时间内,服务是不可用的,对于用户来说是非常不友好的。而kubernetes滚动更新,…...

Java智慧工地APP源码带AI识别
智慧工地为建筑全生命周期赋能,用创新的可视化与智能化方法,降低成本,创造价值。 一、智慧工地APP概述 智慧工地”立足于互联网,采用云计算,大数据和物联网等技术手段,针对当前建筑行业的特点,…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
