P8642 [蓝桥杯 2016 国 AC] 路径之谜
[蓝桥杯 2016 国 AC] 路径之谜
题目描述
小明冒充 X X X 星球的骑士,进入了一个奇怪的城堡。
城堡里边什么都没有,只有方形石头铺成的地面。
假设城堡地面是 n × n n\times n n×n 个方格。如图所示。
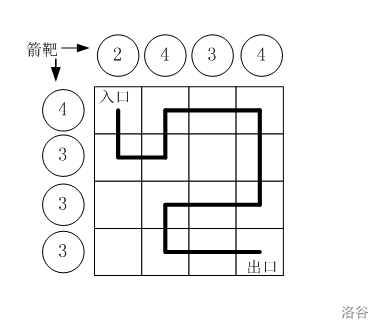
按习俗,骑士要从西北角走到东南角。
可以横向或纵向移动,但不能斜着走,也不能跳跃。
每走到一个新方格,就要向正北方和正西方各射一箭。
(城堡的西墙和北墙内各有 n n n 个靶子)
同一个方格只允许经过一次。但不必做完所有的方格。
如果只给出靶子上箭的数目,你能推断出骑士的行走路线吗?
有时是可以的,比如如图中的例子。
本题的要求就是已知箭靶数字,求骑士的行走路径(测试数据保证路径唯一)
输入格式
第一行一个整数 N ( 0 < N < 20 ) N(0<N<20) N(0<N<20),表示地面有 N × N N \times N N×N 个方格。
第二行 N N N 个整数,空格分开,表示北边的箭靶上的数字(自西向东)
第三行 N N N 个整数,空格分开,表示西边的箭靶上的数字(自北向南)
输出格式
一行若干个整数,表示骑士路径。
为了方便表示,我们约定每个小格子用一个数字代表,从西北角开始编号 $:0,1,2,3 \cdots $。
比如,图中的方块编号为:
0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15
样例 #1
样例输入 #1
4
2 4 3 4
4 3 3 3
样例输出 #1
0 4 5 1 2 3 7 11 10 9 13 14 15
提示
时限 1 秒, 256M。蓝桥杯 2016 年第七届国赛
众所周知,蓝桥杯奖水题不水
经过两个小时的折磨,终于做出来了,网上的题解能不能先把题目过了再发。。
使用dfs,运用减枝,开四个数组来标记,然后就是dfs常规的了,但是题目各种细节,使人心力交瘁
#include<bits/stdc++.h>
using namespace std;
const int N=25;
int g[N][N];
bool vis[N][N];
int path[450];
int n,cnt,k;
bool f;
int ax[N],ay[N];
int bx[N],by[N];
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};
bool check()
{for(int i=1;i<=n;i++){if(bx[i]!=ax[i]||by[i]!=ay[i])return 0;}return 1;
}void dfs(int x,int y)
{if(f) return ;if(x==n&&y==n&&check()){for(int i=0;i<cnt;i++)cout<<path[i]<<" ";f=1;return;}for(int i=0;i<4;i++){int xxx=x+dx[i],yyy=y+dy[i];if(vis[xxx][yyy]||xxx<1||xxx>n||yyy<1||yyy>n||bx[xxx]>=ax[xxx]||by[yyy]>=ay[yyy])continue;bx[xxx] ++;by[yyy] ++;vis[xxx][yyy]=true;path[cnt++]=g[xxx][yyy];dfs(xxx,yyy);bx[xxx] --;by[yyy] --;vis[xxx][yyy]=false;path[cnt--]=-1; }}
int main()
{cin>>n;for(int i=1;i<=n;i++)cin>>ay[i];for(int i=1;i<=n;i++)cin>>ax[i];for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){g[i][j]=k++;}}vis[1][1]=true;path[0]=0;cout<<"0"<<" ";bx[1]=1,by[1]=1;dfs(1,1);return 0;
}
相关文章:

P8642 [蓝桥杯 2016 国 AC] 路径之谜
[蓝桥杯 2016 国 AC] 路径之谜 题目描述 小明冒充 X X X 星球的骑士,进入了一个奇怪的城堡。 城堡里边什么都没有,只有方形石头铺成的地面。 假设城堡地面是 n n n\times n nn 个方格。如图所示。 按习俗,骑士要从西北角走到东南角。 …...
oracle sql developer批量删除某个用户
随着navicate收费,还得破解,pl/sql developer配置麻烦,最近使用oracle sql developer来试试oracle的操作如何; 用着还行,没有卡顿现象, 最近要oracle sql developer批量删除某个用户下所有的表࿰…...
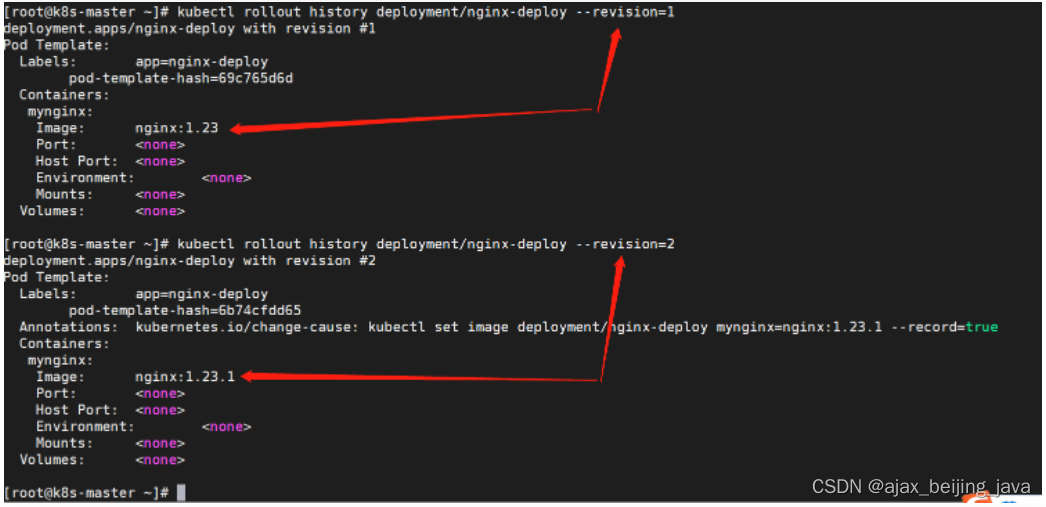
k8s 滚动更新控制(一)
在传统的应用升级时,通常采用的方式是先停止服务,然后升级部署,最后将新应用启动。这个过程面临一个问题,就是在某段时间内,服务是不可用的,对于用户来说是非常不友好的。而kubernetes滚动更新,…...

Java智慧工地APP源码带AI识别
智慧工地为建筑全生命周期赋能,用创新的可视化与智能化方法,降低成本,创造价值。 一、智慧工地APP概述 智慧工地”立足于互联网,采用云计算,大数据和物联网等技术手段,针对当前建筑行业的特点,…...

ME3116电源小板
最近设计一款PCB的时候使用微盟的dc dc电源ic踩了一个坑。 在使用me3116作为24v到5v的降压ic作为esp32系统前级的降压电路时,再没有铂电阻采样负载的情景下工作正常,带上负载后,ic工作不正常,过一段时间,后级电路会烧…...
摸准天气“小心思”,躲避恶劣天气“偷袭”
打开天气预报一看,天气真的很“善变”,既是高温又暴雨,偶尔还有台风路过,“蒸”的让人太太太难受了。看着天气在放晴和即将下雨之间“徘徊”,总是纠结带不带雨伞,让我的每次出门都成了一场冒险之旅。 持…...
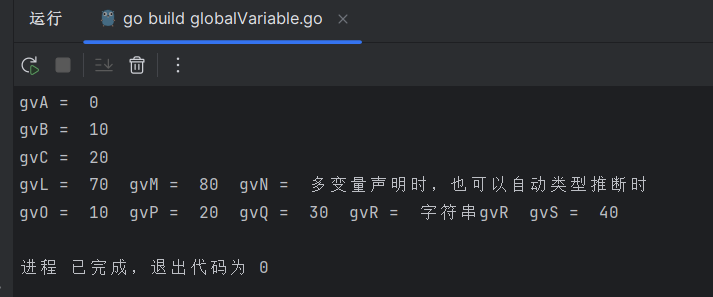
Golang 局部变量、全局变量 声明
文章目录 一、局部变量二、全局变量 一、局部变量 四种声明方式 多变量声明: package mainimport "fmt"//局部变量声明 func main() {//方法一: 声明一个变量和数据类型,不初始化值;默认值为0;var lvA intfmt.Printl…...
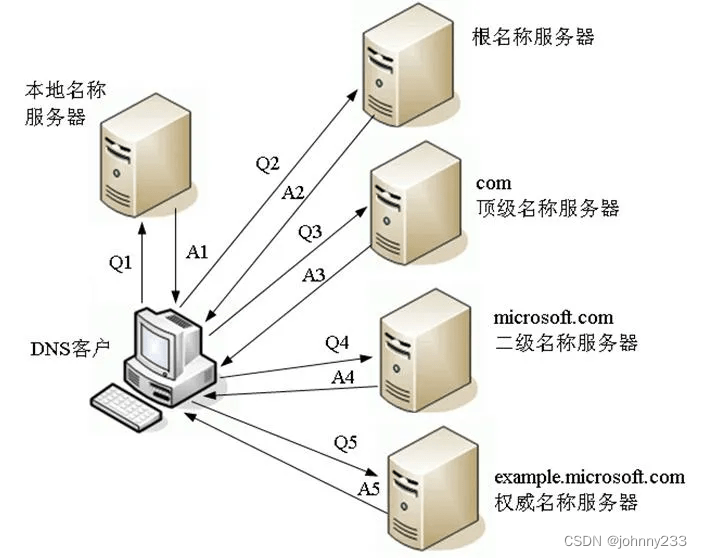
软考高级之系统架构师之数据通信与计算机网络
概念 OSPF 在划分区域之后,OSPF网络中的非主干区域中的路由器对于到外部网络的路由,一定要通过ABR(区域边界路由器)来转发,既然如此,对于区域内的路由器来说,就没有必要知道通往外部网络的详细路由,只要由…...
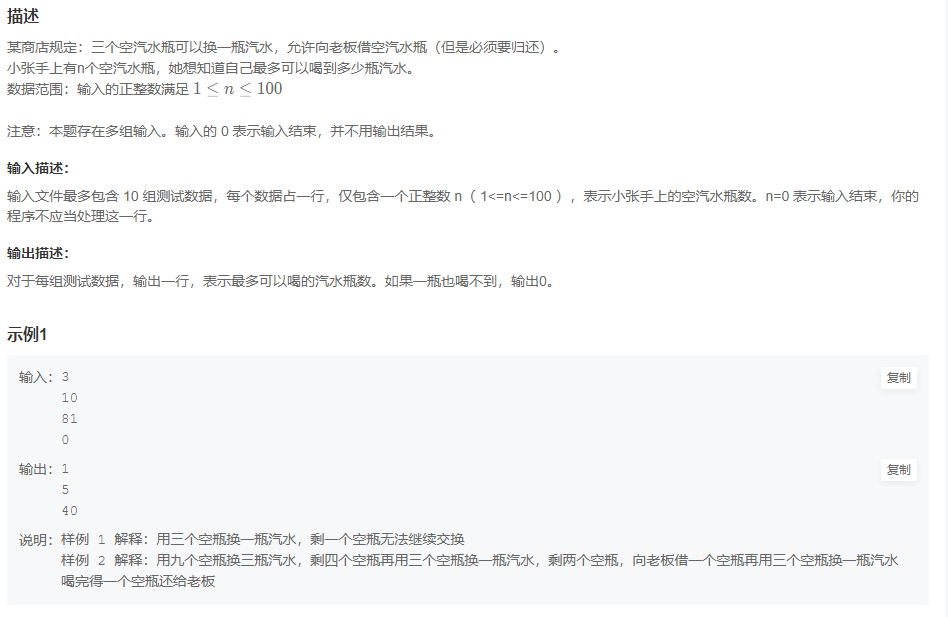
牛客网华为OD前端岗位,面试题库练习记录01
题目一 质数因子 功能:输入一个正整数,按照从小到大的顺序输出它的所有质因子(重复的也要列举)(如180的质因子为2 2 3 3 5 ) JavaScript Node ACM模式 const rl require("readline").createInterface({ i…...

Python web实战之Django 的缓存机制详解
关键词:Python、Web 开发、Django、缓存 1. 缓存是什么?为什么需要缓存? 在 Web 开发中,缓存是一种用于存储数据的临时存储区域。它可以提高应用程序的性能和响应速度,减轻服务器的负载。 当用户访问网页时ÿ…...

chatserver服务器开发笔记
chatserver服务器开发笔记 1 chatserver2 开发环境3 编译 1 chatserver 集群聊天服务器和客户端代码,基于muduo、redis、mysql实现。 学习于https://fixbug.ke.qq.com/ 本人已经挂github:https://github.com/ZixinChen-S/chatserver/tree/main 需要该项…...

DP——动态规划
DP——动态规划 动态规划算法动态规划的一般步骤特殊DP——背包0-1背包问题完全背包问题 总结 动态规划算法 当涉及到解决具有重叠子问题的优化问题时,动态规划是一种常用的算法技术。它通过将问题分解为一系列重叠子问题,并使用递归或迭代的方式来解决…...
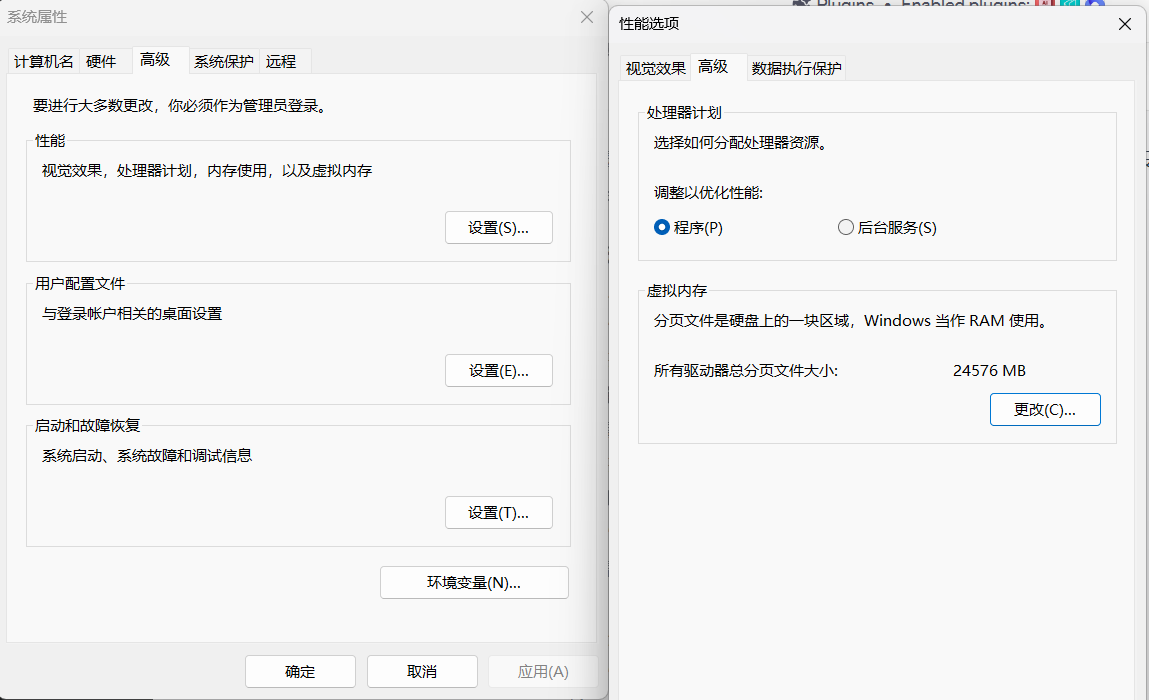
【Windows 11】安装 Android子系统 和 Linux子系统
本文使用电脑系统: 文章目录 一、安卓子系统1.1 安装 WSA1.2 使用 二、Linux子系统2.1 安装 WSL 以及WSL 相关概念2.2 安装一个Linux发行版2.21 从Microsoft Store 安装2.22 用命令安装 2.23 拓展 三、拓展3.1 存储位置3.2 虚拟化技术3.3 Windows 虚拟内存3.3 wsl …...
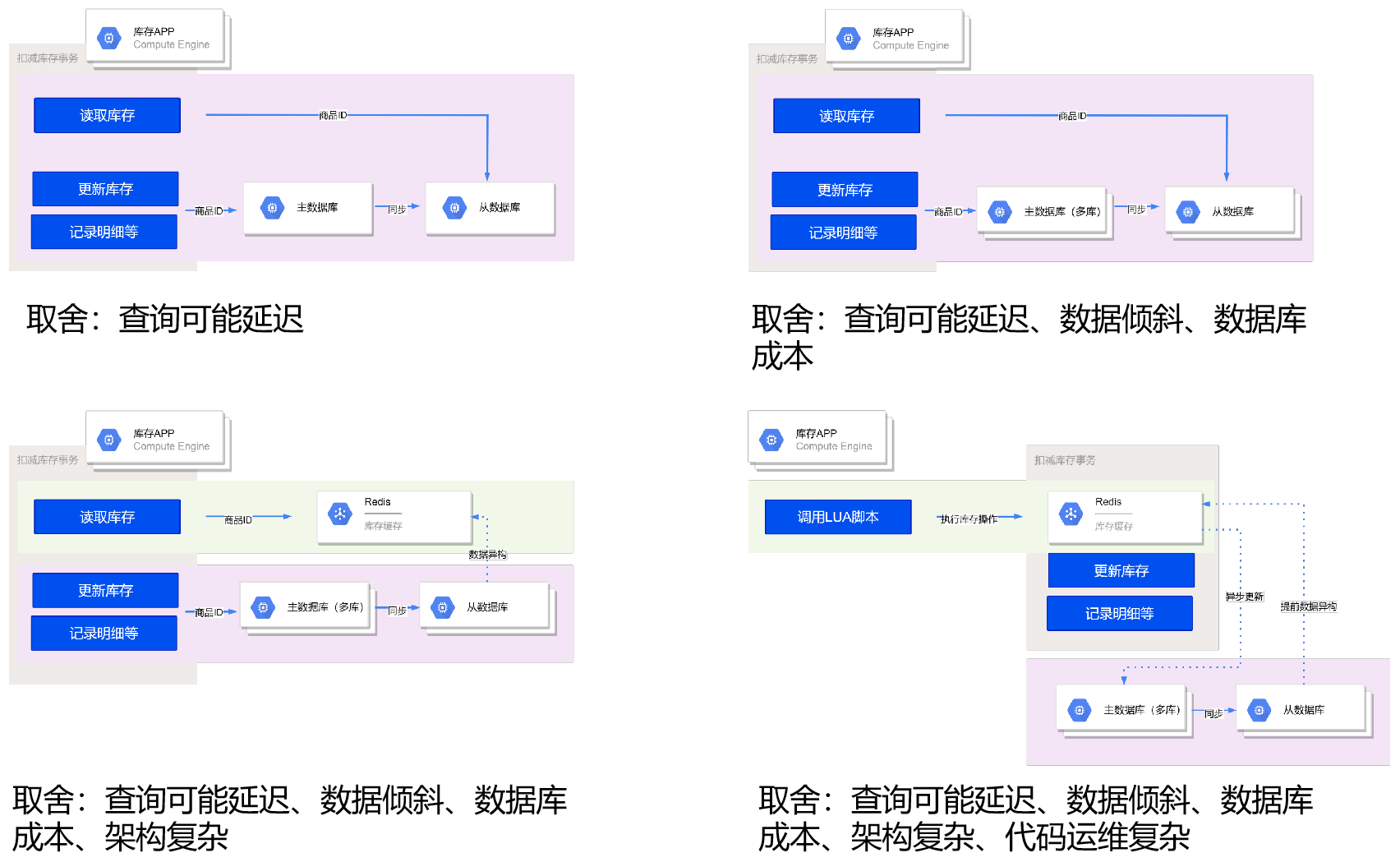
秒杀库存解决方案
电商系统中秒杀是一种常见的业务场景需求,其中核心设计之一就是如何扣减库存。本篇主要分享一些常见库存扣减技术方案,库存扣减设计选择并非一味追求性能更佳,更多的应该考虑根据实际情况来进行架构取舍。在商品购买的过程中,库存…...

[免费在线] 将 PDF 转换为 Excel 或 Excel 转换为 PDF | 5 工具
有了免费的在线 PDF 转换器,您可以轻松免费在线将 PDF 转换为 Excel 或 Excel 转换为 PDF。这篇文章为您筛选了 5 个最常用的工具。要从存储介质恢复错误删除或丢失的 PDF 文档、Excel 电子表格、Word 文件或任何其他文件,您可以使用免费的数据恢复程序 …...
PLC求解弹簧质量模型微分方程数值解(RK4梯形图程序)
微分方程的数值求解,属于数学分析类课程涉及的内容。大家可以参看相关书籍对Runge-Kutta法的介绍,弹簧质量阻尼模型详细的微分方程介绍可以查看下面文章,链接如下: 弹簧质量阻尼系统前馈PID位置控制(PLC闭环仿真SCL+ST代码)_RXXW_Dor的博客-CSDN博客带前馈控制的博途PID程…...

CSDN编程题-每日一练(2023-08-14)
CSDN编程题-每日一练(2023-08-14) 一、题目名称:小股炒股二、题目名称:王子闯闸门三、题目名称:圆小艺 一、题目名称:小股炒股 时间限制:1000ms内存限制:256M 题目描述: …...

【SA8295P 源码分析】69 - Android 侧添加支持 busybox telnetd 服务
【SA8295P 源码分析】69 - Android 侧添加支持 busybox telnetd 服务 一、下载 busybox-1.36.1.tar.bz2 源码包二、编译 busybox 源码三、将编译后的 busybox 打包编入Android 镜像中系列文章汇总见:《【SA8295P 源码分析】00 - 系列文章链接汇总》 本文链接:《【SA8295P 源码…...

OpenCV图像处理——模版匹配和霍夫变换
目录 模版匹配原理实现 霍夫变换霍夫线检测 模版匹配 原理 实现 rescv.matchTemplate(img,template,method)import numpy as np import cv2 as cv import matplotlib.pyplot as pltimgcv.imread(./汪学长的随堂资料/6/模板匹配/lena.jpg) templatecv.imread(./汪学长的随堂资…...
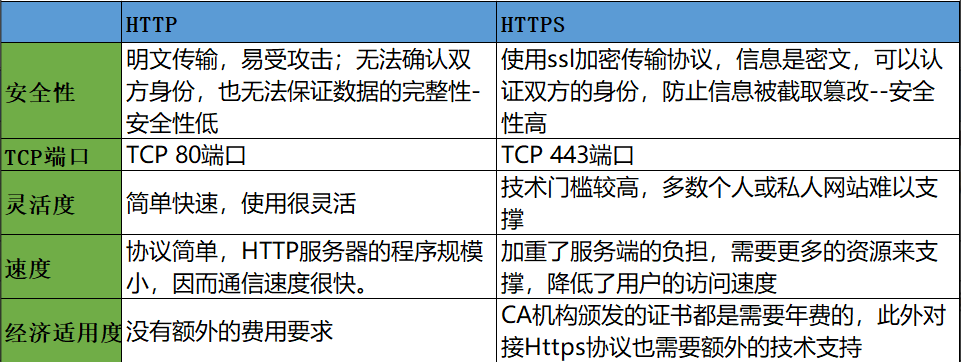
面试官的几句话,差点让我挂在HTTPS上
♥ 前 言 作为软件测试,大家都知道一些常用的网络协议是我们必须要了解和掌握的,比如 HTTP 协议,HTTPS 协议就是两个使用非常广泛的协议,所以也是面试官问的面试的时候问的比较多的两个协议;而且因为这两个协议有相…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

鸿蒙Navigation路由导航-基本使用介绍
1. Navigation介绍 Navigation组件是路由导航的根视图容器,一般作为Page页面的根容器使用,其内部默认包含了标题栏、内容区和工具栏,其中内容区默认首页显示导航内容(Navigation的子组件)或非首页显示(Nav…...
:处理原始数据命令)
ffmpeg(三):处理原始数据命令
FFmpeg 可以直接处理原始音频和视频数据(Raw PCM、YUV 等),常见场景包括: 将原始 YUV 图像编码为 H.264 视频将 PCM 音频编码为 AAC 或 MP3对原始音视频数据进行封装(如封装为 MP4、TS) 处理原始 YUV 视频…...

Linux【5】-----编译和烧写Linux系统镜像(RK3568)
参考:讯为 1、文件系统 不同的文件系统组成了:debian、ubuntu、buildroot、qt等系统 每个文件系统的uboot和kernel是一样的 2、源码目录介绍 目录 3、正式编译 编译脚本build.sh 帮助内容如下: Available options: uboot …...

ABB馈线保护 REJ601 BD446NN1XG
配电网基本量程数字继电器 REJ601是一种专用馈线保护继电器,用于保护一次和二次配电网络中的公用事业和工业电力系统。该继电器在一个单元中提供了保护和监控功能的优化组合,具有同类产品中最佳的性能和可用性。 REJ601是一种专用馈线保护继电器…...

实现p2p的webrtc-srs版本
1. 基本知识 1.1 webrtc 一、WebRTC的本质:实时通信的“网络协议栈”类比 将WebRTC类比为Linux网络协议栈极具洞察力,二者在架构设计和功能定位上高度相似: 分层协议栈架构 Linux网络协议栈:从底层物理层到应用层(如…...

Linux实现线程同步的方式有哪些?
什么是线程同步? 想象一下超市收银台:如果所有顾客(线程)同时挤向同一个收银台(共享资源),场面会一片混乱。线程同步就是给顾客们发"排队号码牌",确保: 有序访…...
