代码随想录第48天 | 198. 打家劫舍、213. 打家劫舍II、337. 打家劫舍III
198. 打家劫舍
当前房屋偷与不偷取决于 前一个房屋和前两个房屋是否被偷了。
递归五部曲:
- dp[i]:考虑下标i(包括i)以内的房屋,最多可以偷窃的金额为dp[i]。
- 决定dp[i]的因素就是第i房间偷还是不偷。
- 如果偷第i房间,那么dp[i] = dp[i - 2] + nums[i] ,即:第i-1房一定是不考虑的,找出 下标i-2(包括i-2)以内的房屋,最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。
- 如果不偷第i房间,那么dp[i] = dp[i - 1],即考 虑i-1房
然后dp[i]取最大值,即dp[i] = max(dp[i - 2] + nums[i], dp[i - 1])
- 递推公式的基础就是dp[0] 和 dp[1]。从dp[i]的定义上来讲,dp[0] 一定是 nums[0],dp[1]就是nums[0]和nums[1]的最大值即:dp[1] = max(nums[0], nums[1])
- dp[i] 是根据dp[i - 2] 和 dp[i - 1] 推导出来的,那么一定是从2开始从前到后遍历
/*** @param {number[]} nums* @return {number}*/
var rob = function (nums) {const len = nums.lengthconst dp = [nums[0], Math.max(nums[0], nums[1])]for (let i = 2; i < len; i++) {dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1])}return dp[len - 1]
};
213. 打家劫舍II
成环的话主要有如下三种情况:
- 考虑不包含首尾元素
- 考虑包含首元素,不包含尾元素
- 考虑包含首元素,不包含尾元素
情况二 和 情况三 都包含了情况一了,所以只考虑情况二和情况三就可以了。剩下的就和普通的打家劫舍一样了。
/*** @param {number[]} nums* @return {number}*/
var rob = function (nums) {const n = nums.lengthif (n === 0) return 0if (n === 1) return nums[0]const result1 = robRange(nums, 0, n - 2)const result2 = robRange(nums, 1, n - 1)return Math.max(result1, result2)
};const robRange = (nums, start, end) => {if (end === start) return nums[start]const dp = new Array(nums.length).fill(0)dp[start] = nums[start]dp[start + 1] = Math.max(nums[start], nums[start + 1])for (let i = start + 2; i <= end; i++) {dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1])}return dp[end]
}
337. 打家劫舍III
使用一个长度为2的数组,记录当前节点偷与不偷所得到的的最大金钱。
递归三部曲:
- 确定递归函数的参数和返回值
要求一个节点 偷与不偷的两个状态所得到的金钱,那么返回值就是一个长度为2的数组。
dp数组(dp table)以及下标的含义:下标为0记录不偷该节点所得到的的最大金钱,下标为1记录偷该节点所得到的的最大金钱。 - 确定终止条件
在遍历的过程中,如果遇到空节点的话,很明显,无论偷还是不偷都是0,所以就返回 - 确定遍历顺序
首先明确的是使用后序遍历。 因为要通过递归函数的返回值来做下一步计算。
通过递归左节点,得到左节点偷与不偷的金钱。
通过递归右节点,得到右节点偷与不偷的金钱。 - 确定单层递归逻辑
如果是偷当前节点,那么左右孩子就不能偷;
如果不偷当前节点,那么左右孩子就可以偷,至于到底偷不偷一定是选一个最大的 - 举例推导dp数组
最后头结点就是 取下标0 和 下标1的最大值就是偷得的最大金钱。
/*** Definition for a binary tree node.* function TreeNode(val, left, right) {* this.val = (val===undefined ? 0 : val)* this.left = (left===undefined ? null : left)* this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @return {number}*/
var rob = function (root) {const postOrder = node => {// 递归出口if (!node) return [0, 0];// 遍历左子树const left = postOrder(node.left);// 遍历右子树const right = postOrder(node.right);// 不偷当前节点,左右子节点都可以偷或不偷,取最大值const DoNot = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);// 偷当前节点,左右子节点只能不偷const Do = node.val + left[0] + right[0];// [不偷,偷]return [DoNot, Do];};const res = postOrder(root);// 返回最大值return Math.max(...res);
};
相关文章:

代码随想录第48天 | 198. 打家劫舍、213. 打家劫舍II、337. 打家劫舍III
198. 打家劫舍 当前房屋偷与不偷取决于 前一个房屋和前两个房屋是否被偷了。 递归五部曲: dp[i]:考虑下标i(包括i)以内的房屋,最多可以偷窃的金额为dp[i]。决定dp[i]的因素就是第i房间偷还是不偷。 如果偷第i房间&…...
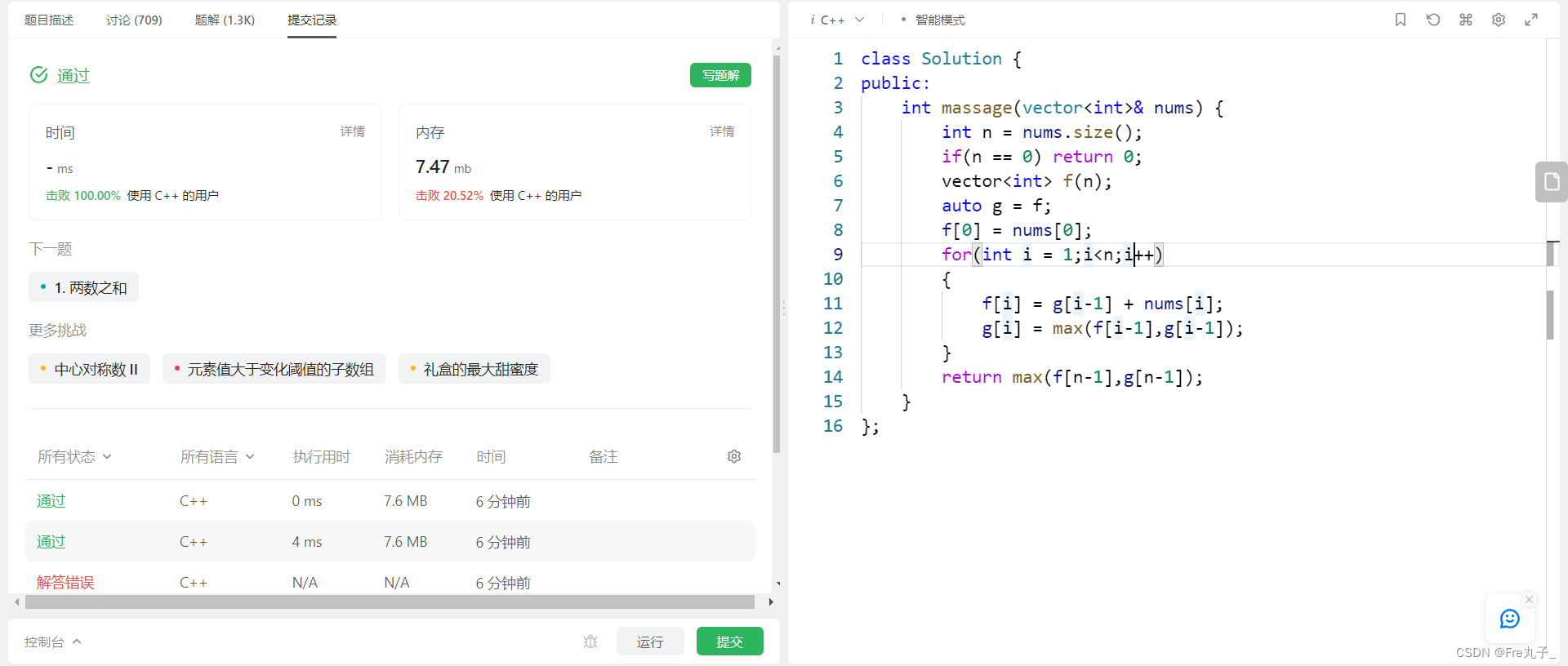
【LeetCode】按摩师
按摩师 题目描述算法分析编程代码 链接: 按摩师 题目描述 算法分析 编程代码 class Solution { public:int massage(vector<int>& nums) {int n nums.size();if(n 0) return 0;vector<int> f(n);auto g f;f[0] nums[0];for(int i 1;i<n;i){f[i] g[i…...

国际腾讯云账号云核算概述!!
云核算概述 维基百科界说:云核算是一种依据互联网的新型核算方法,经过互联网上异构、自治的服务为个人和企业供给按需即取的核算。 云核算描绘的一起特征:云是一种按需运用的服务,运用者只重视服务本身。 云核算作为IT服务形式&am…...

.NET 6.0 重启 IIS 进程池
在 .NET 6.0 中,你可以使用 Microsoft.Web.Administration 命名空间提供的 API 来管理 IIS 进程池并实现重启操作。以下是一个示例代码,展示如何使用 .NET 6.0 中的 Microsoft.Web.Administration 来重启 IIS 进程池: using Microsoft.Web.A…...

一位心理学教师对ChatGPT的看法,提到了正确地使用它的几个要点
在没有自主学习能力和有自主学习能力的两类学生中,ChatGPT的出现,会加大他们在知识学习及思维发展上的鸿沟。爱学习的人会因为AI变得更好…… 从2022年年底起,ChatGPT的技术突破使人类终于进入了一个AI被广泛应用在工作、学习、生活的时代。…...

认识Node.js及三个模块
文章目录 1.初识 Node.js1.1 什么是 Node.js1.2 Node.js 中的 JavaScript 运行环境1.3 Node.js 可以做什么1.4 Node.js 环境的安装1.4.1 区分 LTS 版本和 Current 版本的不同1.4.2 查看已安装的 Node.js 的版本号1.4.3 什么是终端1.4.4 终端中的快捷键 1.5 在 Node.js 环境中执…...

49 | 公司销售数据分析
公司销售数据分析报告 本数据是2012~2014年间一家生产体育类产品的全球销售订单数据,分别按时间、产品类别、销售国家统计产品销售情况,分析销售额和利润额统计各产品市场占有份额,为下一步生产计划提供有价值的建议。 数据大小:88475 行, 11 列 Retailer country销售国…...
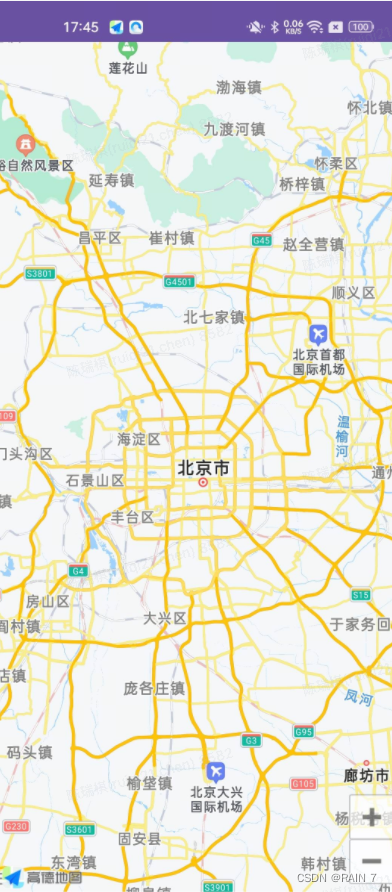
Android 项目导入高德SDK初次上手
文章目录 一、前置知识:二、学习目标三、学习资料四、操作过程1、创建空项目2、高德 SDK 环境接入2.1 获取高德 key2.2下载 SDK 并导入2.2.1、下载SDK 文件2.2.2、SDK 导入项目2.2.3、清单文件配置2.2.4、隐私权限 3、显示地图 一、前置知识: 1、Java 基…...
)
生成树协议用来解决网络风暴的问题?(第三十二课)
生成树协议用来解决网络风暴的问题?(第三十二课) 一 STP RSTP MSTP 介绍 STP(Spanning Tree Protocol)、RSTP(Rapid Spanning Tree Protocol)和MSTP(Multiple Spanning Tree Protocol)都是用于网络中避免环路的协议。 STP是最初的协议,它通过将某些端口阻塞来防止…...

git分支操作
Git分支的操作 1.1 Git分支简介 Git分支是由指针管理起来的,所以创建、切换、合并、删除分支都非常快,非常适合大型项目的开发。 在分支上做开发,调试好了后再合并到主分支。那么每个人开发模块式都不会影响到别人。 分支使用策略…...

【基础学习笔记 enum】TypeScript 中的 enum 枚举类型介绍
因为之前网上查好多博客都是只说最基础的,所以这里记录一下,最基础的放在最后面。 这里重点要记录的是枚举成员的值可以是字符串(字符串枚举,因为网上大部分只介绍常数枚举),需要注意的一点是,…...
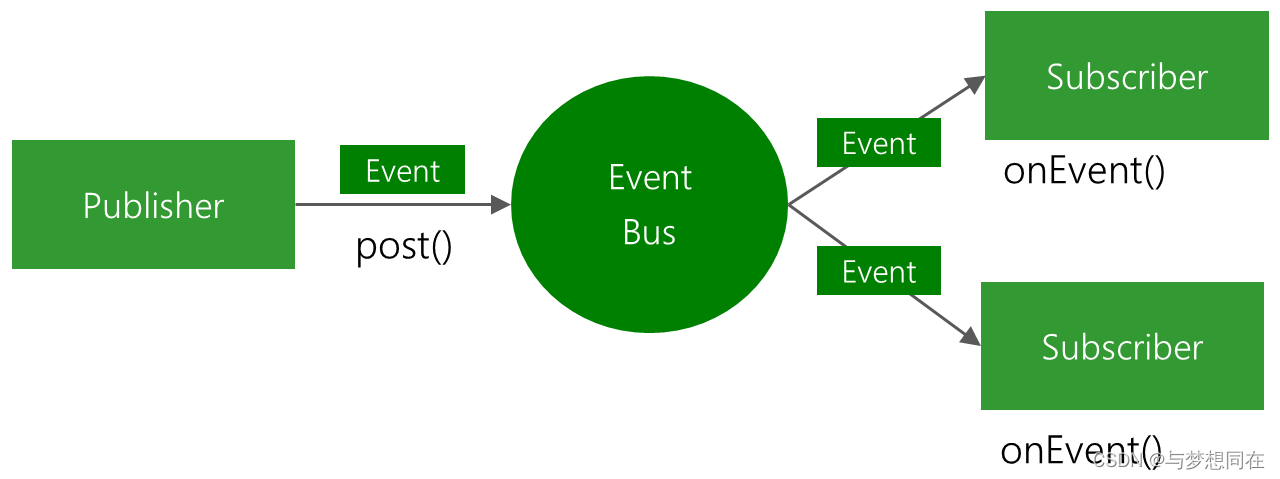
SpringBoot中间件使用之EventBus、Metric、CommandLineRunner
1、EventBus 使用EventBus 事件总线的方式可以实现消息的发布/订阅功能,EventBus是一个轻量级的消息服务组件,适用于Android和Java。 // 1.注册事件通过 EventBus.getDefault().register(); // 2.发布事件 EventBus.getDefault().post(“事件内容”); …...

ffmpeg命令行是如何打开vf_scale滤镜的
前言 在ffmpeg命令行中,ffmpeg -i test -pix_fmt rgb24 test.rgb,会自动打开ff_vf_scale滤镜,本章主要追踪这个流程。 通过gdb可以发现其基本调用栈如下: 可以看到,query_formats()中创建的v…...
【Vue3】自动引入插件-`unplugin-auto-import`
Vue3自动引入插件-unplugin-auto-import,不必再手动 import 。 自动导入 api 按需为 Vite, Webpack, Rspack, Rollup 和 esbuild 。支持TypeScript。由unplugin驱动。 插件安装:unplugin-auto-import 配置vite.config.ts(配置完后需要重启…...

每日温度(力扣)单调栈 JAVA
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。 示例 1: 输入: temperatur…...
博客项目(Spring Boot)
1.需求分析 注册功能(添加用户操纵)登录功能(查询操作)我的文章列表页(查询我的文章|文章修改|文章详情|文章删除)博客编辑页(添加文章操作)所有人博客列表(带分页功能)…...

修改Jenkins存储目录
注意:在Jenkins运行时是不能更改的. 请先将Jenkins停止运行。 1、windows环境下更改JENKINS的主目录 Windows环境中,Jenkins主目录默认在C:Documents and SettingsAAA.jenkins 。可以通过设置环境变量来修改,例如: JENKINS_HOME…...
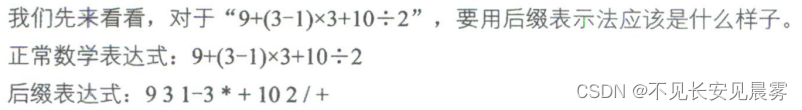
数据结构【第4章】——栈与队列
队列是只允许在一端进行插入操作、而在另-端进行删除操作的线性表。 栈 栈与队列:栈是限定仅在表尾进行插入和删除操作的线性表。 我们把允许插入和删除的一端称为栈顶(top),另一端称为栈底(bottom)&…...

android webview 显示灰度网页
要在WebView中显示网页灰度显示,您可以通过以下步骤操作: 在您的布局文件中添加WebView组件: <WebViewandroid:id"id/webview"android:layout_width"match_parent"android:layout_height"match_parent" /…...
)
Linux操作系统的基础使用技能的训练大纲(超级详细版本适合于初学者)
RHCE红帽认证工程师课程对应考试课 程 纲 要 第一部分 网络基础 RH033RH302 Linux基础: 1) 在bashshell命令行模式下运行基本的Linux命令 2) 从命令行及GNOME界面启动应用程序 3) 使用及配置Xwindow系统及GNOME桌面环境 4) 使用GNOME GUI应用程序完成一般的工作 5) 了解Linu…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
