【量化课程】02_4.数理统计的基本概念
2.4_数理统计的基本概念
数理统计思维导图
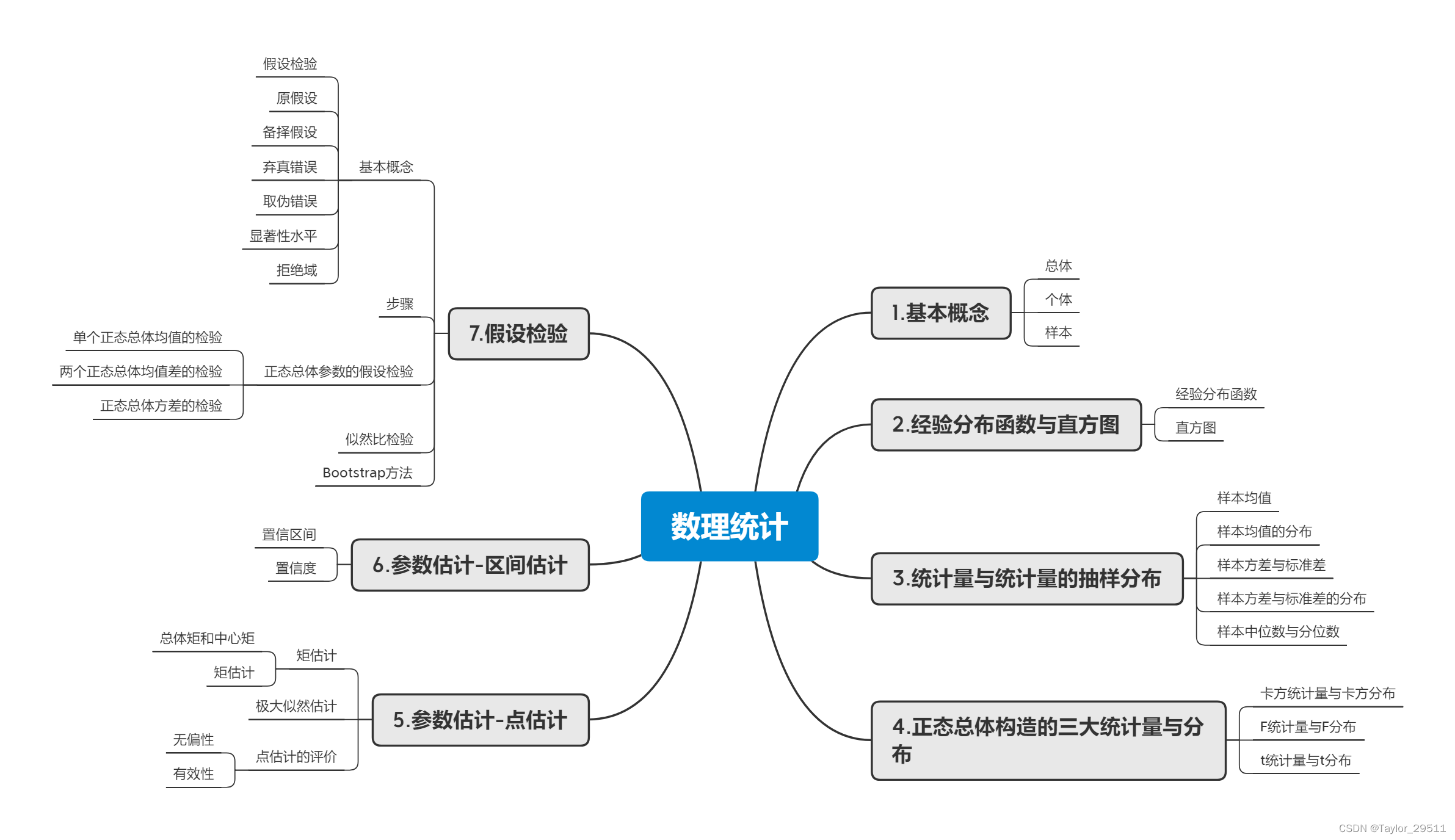
更多详细内容见notebook
1.基本概念
总体:研究对象的全体,它是一个随机变量,用 X X X表示。
个体:组成总体的每个基本元素。
简单随机样本:来自总体 X X X的 n n n个相互独立且与总体同分布的随机变量 X 1 , X 2 ⋯ , X n X_{1},X_{2}\cdots,X_{n} X1,X2⋯,Xn,称为容量为 n n n的简单随机样本,简称样本。
统计量:设 X 1 , X 2 ⋯ , X n , X_{1},X_{2}\cdots,X_{n}, X1,X2⋯,Xn,是来自总体 X X X的一个样本, g ( X 1 , X 2 ⋯ , X n ) g(X_{1},X_{2}\cdots,X_{n}) g(X1,X2⋯,Xn))是样本的连续函数,且 g ( ) g() g()中不含任何未知参数,则称 g ( X 1 , X 2 ⋯ , X n ) g(X_{1},X_{2}\cdots,X_{n}) g(X1,X2⋯,Xn)为统计量。
样本均值:
X ‾ = 1 n ∑ i = 1 n X i \overline{X} = \frac{1}{n}\sum_{i = 1}^{n}X_{i} X=n1∑i=1nXi
样本方差: S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ‾ ) 2 S^{2} = \frac{1}{n - 1}\sum_{i = 1}^{n}{(X_{i} - \overline{X})}^{2} S2=n−11∑i=1n(Xi−X)2
样本矩:样本 k k k阶原点矩: A k = 1 n ∑ i = 1 n X i k , k = 1 , 2 , ⋯ A_{k} = \frac{1}{n}\sum_{i = 1}^{n}X_{i}^{k},k = 1,2,\cdots Ak=n1∑i=1nXik,k=1,2,⋯
样本 k k k阶中心矩: B k = 1 n ∑ i = 1 n ( X i − X ‾ ) k , k = 1 , 2 , ⋯ B_{k} = \frac{1}{n}\sum_{i = 1}^{n}{(X_{i} - \overline{X})}^{k},k = 1,2,\cdots Bk=n1∑i=1n(Xi−X)k,k=1,2,⋯
2.分布
χ 2 \chi^{2} χ2分布: χ 2 = X 1 2 + X 2 2 + ⋯ + X n 2 ∼ χ 2 ( n ) \chi^{2} = X_{1}^{2} + X_{2}^{2} + \cdots + X_{n}^{2}\sim\chi^{2}(n) χ2=X12+X22+⋯+Xn2∼χ2(n),其中 X 1 , X 2 ⋯ , X n , X_{1},X_{2}\cdots,X_{n}, X1,X2⋯,Xn,相互独立,且同服从 N ( 0 , 1 ) N(0,1) N(0,1)
t t t分布: T = X Y / n ∼ t ( n ) T = \frac{X}{\sqrt{Y/n}}\sim t(n) T=Y/nX∼t(n) ,其中 X ∼ N ( 0 , 1 ) , Y ∼ χ 2 ( n ) , X\sim N\left( 0,1 \right),Y\sim\chi^{2}(n), X∼N(0,1),Y∼χ2(n),且 X X X, Y Y Y 相互独立。
F F F分布: F = X / n 1 Y / n 2 ∼ F ( n 1 , n 2 ) F = \frac{X/n_{1}}{Y/n_{2}}\sim F(n_{1},n_{2}) F=Y/n2X/n1∼F(n1,n2),其中 X ∼ χ 2 ( n 1 ) , Y ∼ χ 2 ( n 2 ) , X\sim\chi^{2}\left( n_{1} \right),Y\sim\chi^{2}(n_{2}), X∼χ2(n1),Y∼χ2(n2),且 X X X, Y Y Y相互独立。
分位数:若 P ( X ≤ x α ) = α , P(X \leq x_{\alpha}) = \alpha, P(X≤xα)=α,则称 x α x_{\alpha} xα为 X X X的 α \alpha α分位数
3.正态总体的常用样本分布
设 X 1 , X 2 ⋯ , X n X_{1},X_{2}\cdots,X_{n} X1,X2⋯,Xn为来自正态总体 N ( μ , σ 2 ) N(\mu,\sigma^{2}) N(μ,σ2)的样本, X ‾ = 1 n ∑ i = 1 n X i , S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ‾ ) 2 , \overline{X} = \frac{1}{n}\sum_{i = 1}^{n}X_{i},S^{2} = \frac{1}{n - 1}\sum_{i = 1}^{n}{{(X_{i} - \overline{X})}^{2},} X=n1∑i=1nXi,S2=n−11∑i=1n(Xi−X)2,则:
(1) X ‾ ∼ N ( μ , σ 2 n ) \overline{X}\sim N\left( \mu,\frac{\sigma^{2}}{n} \right){\ \ } X∼N(μ,nσ2) 或者 X ‾ − μ σ n ∼ N ( 0 , 1 ) \frac{\overline{X} - \mu}{\frac{\sigma}{\sqrt{n}}}\sim N(0,1) nσX−μ∼N(0,1)
(2) ( n − 1 ) S 2 σ 2 = 1 σ 2 ∑ i = 1 n ( X i − X ‾ ) 2 ∼ χ 2 ( n − 1 ) \frac{(n - 1)S^{2}}{\sigma^{2}} = \frac{1}{\sigma^{2}}\sum_{i = 1}^{n}{{(X_{i} - \overline{X})}^{2}\sim\chi^{2}(n - 1)} σ2(n−1)S2=σ21∑i=1n(Xi−X)2∼χ2(n−1)
(3) 1 σ 2 ∑ i = 1 n ( X i − μ ) 2 ∼ χ 2 ( n ) \frac{1}{\sigma^{2}}\sum_{i = 1}^{n}{{(X_{i} - \mu)}^{2}\sim\chi^{2}(n)} σ21∑i=1n(Xi−μ)2∼χ2(n)
(4) X ‾ − μ S / n ∼ t ( n − 1 ) {\ \ }\frac{\overline{X} - \mu}{S/\sqrt{n}}\sim t(n - 1) S/nX−μ∼t(n−1)
4.重要公式与结论
(1) 对于 χ 2 ∼ χ 2 ( n ) \chi^{2}\sim\chi^{2}(n) χ2∼χ2(n),有 E ( χ 2 ( n ) ) = n , D ( χ 2 ( n ) ) = 2 n ; E(\chi^{2}(n)) = n,D(\chi^{2}(n)) = 2n; E(χ2(n))=n,D(χ2(n))=2n;
(2) 对于 T ∼ t ( n ) T\sim t(n) T∼t(n),有 E ( T ) = 0 , D ( T ) = n n − 2 ( n > 2 ) E(T) = 0,D(T) = \frac{n}{n - 2}(n > 2) E(T)=0,D(T)=n−2n(n>2);
(3) 对于 F ~ F ( m , n ) F\tilde{\ }F(m,n) F ~F(m,n),有 1 F ∼ F ( n , m ) , F a / 2 ( m , n ) = 1 F 1 − a / 2 ( n , m ) ; \frac{1}{F}\sim F(n,m),F_{a/2}(m,n) = \frac{1}{F_{1 - a/2}(n,m)}; F1∼F(n,m),Fa/2(m,n)=F1−a/2(n,m)1;
(4) 对于任意总体 X X X,有 E ( X ‾ ) = E ( X ) , E ( S 2 ) = D ( X ) , D ( X ‾ ) = D ( X ) n E(\overline{X}) = E(X),E(S^{2}) = D(X),D(\overline{X}) = \frac{D(X)}{n} E(X)=E(X),E(S2)=D(X),D(X)=nD(X)
相关文章:

【量化课程】02_4.数理统计的基本概念
2.4_数理统计的基本概念 数理统计思维导图 更多详细内容见notebook 1.基本概念 总体:研究对象的全体,它是一个随机变量,用 X X X表示。 个体:组成总体的每个基本元素。 简单随机样本:来自总体 X X X的 n n n个相互…...

【计算机视觉|生成对抗】改进的生成对抗网络(GANs)训练技术
本系列博文为深度学习/计算机视觉论文笔记,转载请注明出处 标题:Improved Techniques for Training GANs 链接:[1606.03498v1] Improved Techniques for Training GANs (arxiv.org) 摘要 本文介绍了一系列应用于生成对抗网络(G…...
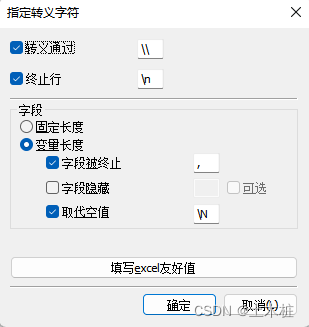
SQLyog中导入CSV文件入库到MySQL中
1.在数据库中新建一个表,设置列名(与待导入文件一致),字段可以多出几个都可以 2.右键表名,导入- - >导入使用本地加载的CSV数据 选择使用加载本地CVS数据 3.指定好转义字符,将终止设置为,号(英文状态下…...

Spring Security6 最新版配置该怎么写,该如何实现动态权限管理
Spring Security 在最近几个版本中配置的写法都有一些变化,很多常见的方法都废弃了,并且将在未来的 Spring Security7 中移除,因此又补充了一些新的内容,重新发一下,供各位使用 Spring Security 的小伙伴们参考。 接下…...

CommandLineRunner 和 ApplicationRunner 用于Spring Boot 应用启动后执行特定逻辑
CommandLineRunner 和 ApplicationRunner 都是 Spring Boot 中用于在应用启动后执行特定逻辑的接口。它们的主要区别在于传递的参数类型和执行顺序。下面我将为您详细解释它们的用途、使用案例以及执行顺序。 CommandLineRunner CommandLineRunner 是一个接口,它有…...
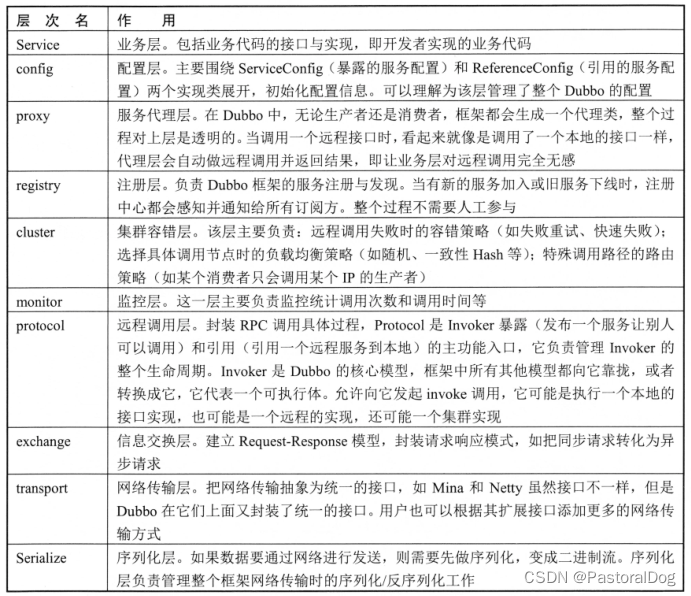
一、Dubbo 简介与架构
一、Dubbo 简介与架构 1.1 应用架构演进过程 单体应用:JEE、MVC分布式应用:SOA、微服务化 1.2 Dubbo 简介一种分布式 RPC 框架,对专业知识(序列化/反序列化、网络、多线程、设计模式、性能优化等)进行了更高层的抽象和…...
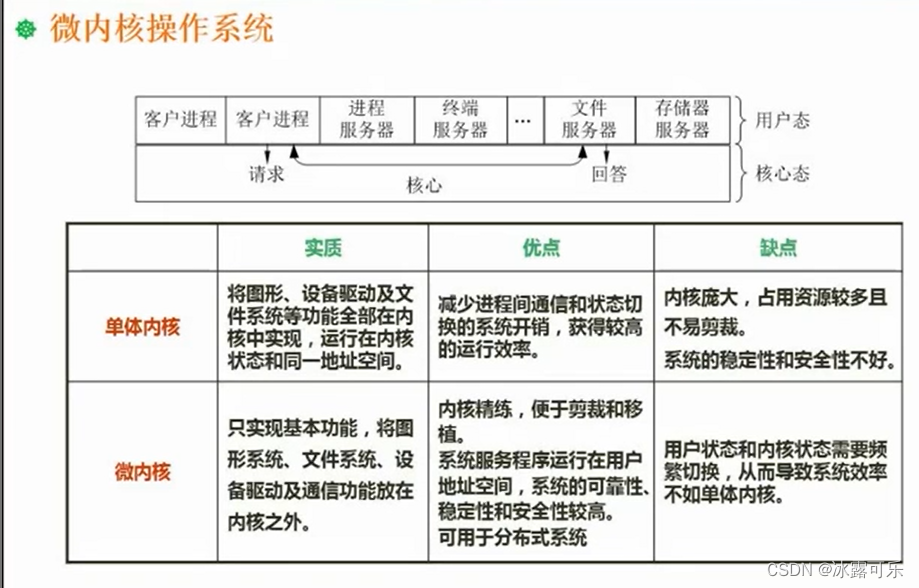
软考:中级软件设计师:文件管理,索引文件结构,树型文件结构,位示图,数据传输方式,微内核
软考:中级软件设计师: 提示:系列被面试官问的问题,我自己当时不会,所以下来自己复盘一下,认真学习和总结,以应对未来更多的可能性 关于互联网大厂的笔试面试,都是需要细心准备的 (1…...

实践-CNN卷积层
实践-CNN卷积层 1 卷积层构造2 整体流程3 BatchNormalization效果4 参数对比5 测试效果 1 卷积层构造 2 整体流程 根据网络结构来写就可以了。 池化 拉平 训练一个网络需要2-3天的时间。用经典网络来,一些细节没有必要去扣。 损失函数: fit模型&…...
【设计模式】MVC 模式
MVC 模式代表 Model-View-Controller(模型-视图-控制器) 模式。这种模式用于应用程序的分层开发。 Model(模型) - 模型代表一个存取数据的对象或 JAVA POJO。它也可以带有逻辑,在数据变化时更新控制器。Viewÿ…...

看康师傅金桔柠檬X国漫IP跨界出圈,打开IP合作新思路
Z世代年轻群体已经成为消费主力,其喜好和消费观念也呈现出全新态势。抓住年轻人的心,就是抓住了品牌未来的战场。 那么到底什么样的营销动作才能真正撬动年轻人? 对于互联网时代成长起来的Z世代年轻人来说,人气二次元IP无疑是能最…...
ElementUI的MessageBox的按钮置灰且不可点击
// this.$confirmthis.$alert(这是一段内容, 标题名称, {confirmButtonText: 确定,confirmButtonCLass: confirmButton,beforeClose: (action,instance,done) > {if (action confirm) {return false} else {done()}});}.confirmButton {background: #ccc !important;cursor…...

pc端与flutter通信失效, Method not found
报错情况描述:pc端与flutter通信,ios端能实现通信,安卓端通信报错 报错通信代码: //app消息通知window.callbackName function (res) {window?.jsBridge && window.jsBridge?.postMessage(JSON.stringify(res), "…...

linux 防火墙经常使用的命令
# 开启防火墙服务 systemctl start firewalld # 关闭防火墙服务 systemctl stop firewalld # 重启防火墙服务 systemctl restart firewalld # 开发端口 firewall-cmd --zonepublic --add-port8080/tcp --permanent # 移除端口 firewall-cmd --zonepublic --remove-port8080/tc…...

Docker desktop安装mysql
首先本地已经有 docker 环境存在,然后可以拉取 MySQL 镜像。 相关 mysql 仓库地址: https://hub.docker.com/_/mysql/ # 镜像拉取 docker pull mysql:8.0.26docker pull mysql:latest# 查看镜像列表docker image ls等待镜像完成之后就可以启动 mysql 了…...
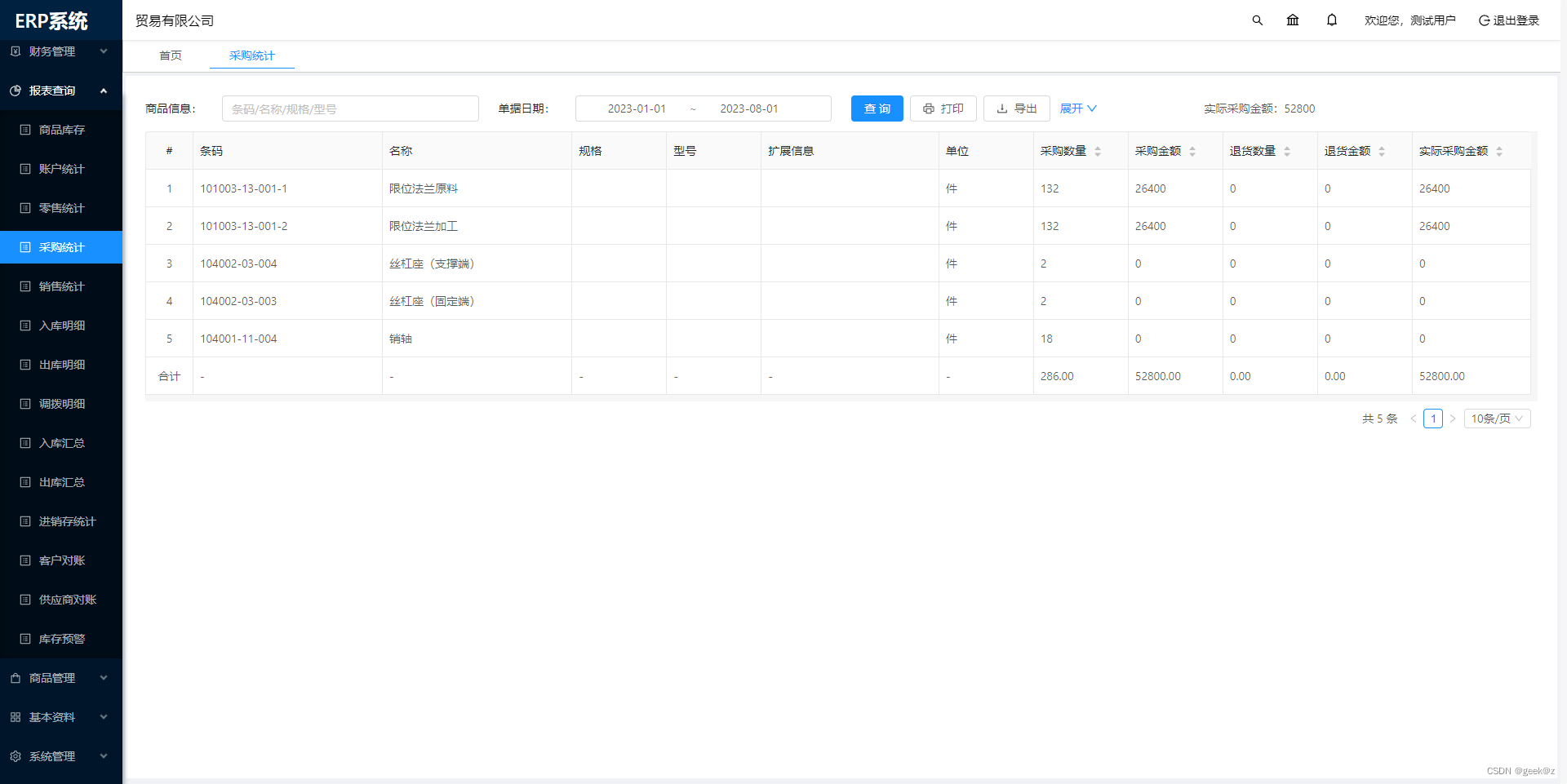
Java SpringBoot Vue ERP系统
系统介绍 该ERP系统基于SpringBoot框架和SaaS模式,支持多租户,专注进销存财务生产功能。主要模块有零售管理、采购管理、销售管理、仓库管理、财务管理、报表查询、系统管理等。支持预付款、收入支出、仓库调拨、组装拆卸、订单等特色功能。拥有商品库存…...

什么是CSS中的渐变(gradient)?如何使用CSS创建线性渐变和径向渐变?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 渐变(Gradient)在CSS中的应用⭐ 线性渐变(Linear Gradient)语法:示例: ⭐ 径向渐变(Radial Gradient)语法:示例: ⭐ 写…...

【深度学习】PyTorch快速入门
【深度学习】学习PyTorch基础 介绍PyTorch 深度学习框架是一种软件工具,旨在简化和加速构建、训练和部署深度学习模型的过程。深度学习框架提供了一系列的函数、类和工具,用于定义、优化和执行各种深度神经网络模型。这些框架帮助研究人员和开发人员专注…...

学习Vue:组件通信
组件化开发在现代前端开发中是一种关键的方法,它能够将复杂的应用程序拆分为更小、更可管理的独立组件。在Vue.js中,父子组件通信是组件化开发中的重要概念,同时我们还会讨论其他组件间通信的方式。 父子组件通信:Props 和 Events…...

springboot项目打包后读取jar包里面的
ResourcePatternResolver resourcePatternResolver new PathMatchingResourcePatternResolver(); Resource[] resources resourcePatternResolver.getResources("classpath*:templates/*.*"); for ( Resource resource : resources ) {//获取文件,在打成…...

设计模式之七大原则
👑单一职责原则 单一职责原则告诉我们一个类应该只有一个责任或者只负责一件事情。 想象一下,如果一个类承担了太多的责任,就像一个人同时负责做饭、洗衣服和打扫卫生一样,那么这个类会变得非常复杂,难以理解和维护。而…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...
