springboot项目打包后读取jar包里面的
ResourcePatternResolver resourcePatternResolver = new PathMatchingResourcePatternResolver();
Resource[] resources = resourcePatternResolver.getResources("classpath*:templates/*.*");
for ( Resource resource : resources ) {//获取文件,在打成jar包后,通过url来获取文件,则路径是正确的File file = new File(resource.getURL().getFile());System.out.println(file.getName());
}
//读取要下载的文件,保存到文件输入流
InputStream inputStream = resourcePatternResolver.getResource(templatePath).getInputStream();
if (ObjectUtil.isEmpty(inputStream)) {throw new RuntimeException("模板不存在");
}相关文章:

springboot项目打包后读取jar包里面的
ResourcePatternResolver resourcePatternResolver new PathMatchingResourcePatternResolver(); Resource[] resources resourcePatternResolver.getResources("classpath*:templates/*.*"); for ( Resource resource : resources ) {//获取文件,在打成…...

设计模式之七大原则
👑单一职责原则 单一职责原则告诉我们一个类应该只有一个责任或者只负责一件事情。 想象一下,如果一个类承担了太多的责任,就像一个人同时负责做饭、洗衣服和打扫卫生一样,那么这个类会变得非常复杂,难以理解和维护。而…...

pytorch入门-TensorBoard和Transforms
TensorBoard from PIL import Image from torch.utils.tensorboard import SummaryWriter from torchvision import transforms# python的用法 -》 tensor数据类型 # 通过transforms.ToTensor 去解决两个问题 # 1. transforms该如何使用(python) # 2. …...

【java】Java基础——接口和实现
当一个类实现一个接口时,必须提供接口中定义的所有方法的具体实现,除非这个类是抽象类。默认方法:default修饰接口中的方法,可实现方法体,在实现接口的类中可以不重写该方法 // 定义一个接口,接口不关心方…...

JetPack Compose 学习笔记(持续整理中...)
1.为什么要学? 1.命令式和声明式 UI大战,个人认为命令式UI自定义程度较高,能更深入到性能,内存优化方面,而申明式UI 是现在主流的设计,比如React,React Native,Flutter,Swift UI等等,现在性能也逐渐在变得更好 2.还有一个原因compose 是KMM 是完整跨平台的UI基础 3.…...

遍历集合List的五种方法以及如何在遍历集合过程中安全移除元素
一、遍历集合List的五种方法 测试数据 List<String> list new ArrayList<>(); list.add("A");list.add("B");list.add("C");1. 普通for循环 普通for循环,通过索引遍历 for (int i 0; i < list.size(); i) {Syst…...

【SQL应知应会】索引(二)• MySQL版
欢迎来到爱书不爱输的程序猿的博客, 本博客致力于知识分享,与更多的人进行学习交流 本文收录于SQL应知应会专栏,本专栏主要用于记录对于数据库的一些学习,有基础也有进阶,有MySQL也有Oracle 索引 • MySQL版 前言一、索引1.简介2.创建2.1 索引…...

Android 简单的视频、图片压缩工具
首页需要压缩的工具包 1.Gradle implementation com.iceteck.silicompressorr:silicompressor:2.2.3 2.添加相关权限(手机得动态申请权限) <uses-permission android:name"android.permission.READ_EXTERNAL_STORAGE"/> <uses-p…...

信息论、推理和机器学习算法之间交叉的经典例子
信息论、推理和机器学习算法之间交叉的经典例子: 熵和信息增益在决策树学习中的应用。信息增益利用熵的概念来评估特征的分类能力,从而指导决策树的增长。 交叉熵在神经网络训练中的广泛使用。它结合信息论与最大似然推断,用于度量预测分布与真实分布之间的距离。 变分推断常被…...
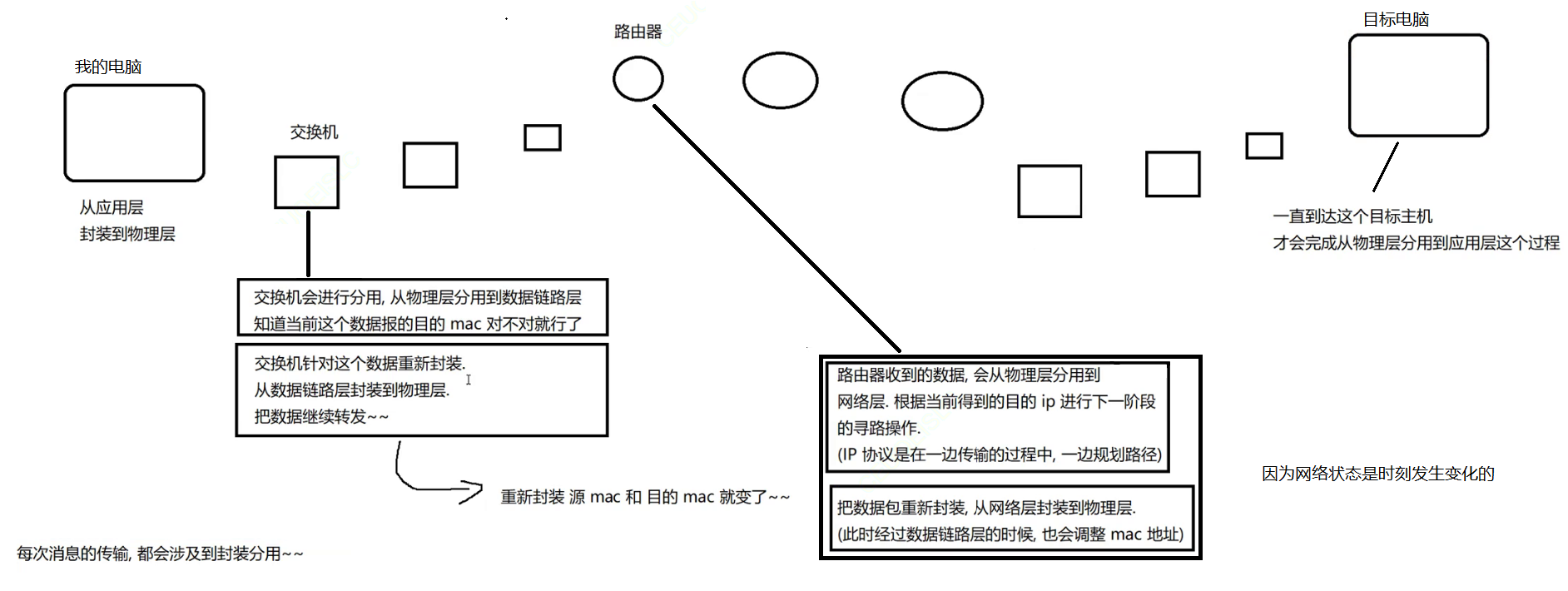
【多线程】网络原理初识
网络原理初识 1. 网络发展史1.2 独立模式1.3 网络互联1.3 局域网1.4 广域网 2. 网络通信基础2.1 IP地址2.2 端口号2.3 认识协议2.4 五元组2.5 协议分层2.5.1 什么是协议分层2.5.2 协议分层的好处2.5.2 OSI七层模型2.5.3 TCP/IP五层模型 2.6 封装和分用2.6.1 封装2.6.1.1 应用层…...

Android之ADB常用命令
15、查看ipv6 是否使能 sysctl -a | grep ipv6 | grep disable 13、以太网获取Ip、网关、子网掩码、域名等 adb shell 网卡信息:ifconfig eth0 dns1:getprop net.dns1 dns2:getprop net.dns2 12、屏幕分辨率:wm size 11、…...
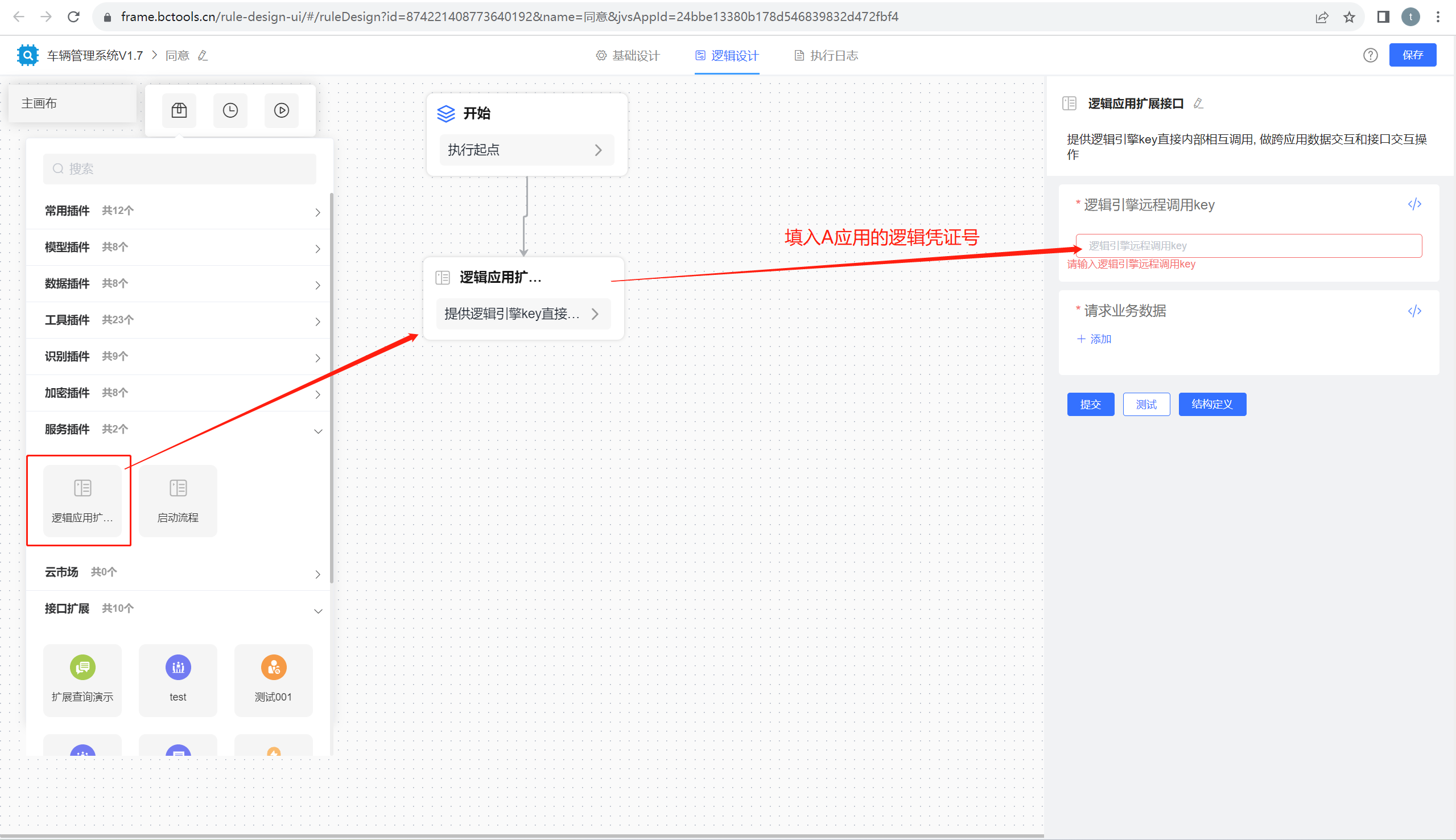
低代码开发工具:JVS轻应用之间如何实现数据的调用?
在低代码开发平台中,如何实现应用之间的数据共享呢?最标准的方式是通过接口,本文介绍JVS轻应用如何实现将数据通过API输出、轻应用如何实现体内API数据的获取?实现方式如下图所示,不管是数据提供方,还是数据…...
在Java中对XML的简单应用
XML 数据传输格式1 XML 概述1.1 什么是 XML1.2 XML 与 HTML 的主要差异1.3 XML 不是对 HTML 的替代 2 XML 语法2.1 基本语法2.2 快速入门2.3 组成部分2.3.1 文档声明格式属性 2.3.2 指令(了解):结合CSS2.3.3 元素2.3.4 属性**XML 元素 vs. 属…...

Linu学习笔记——常用命令
Linux 常用命令全拼: Linux 常用命令全拼 | 菜鸟教程 一、切换root用户 1.给root用户设置密码 sudo passwd root 2.输入密码,并确认密码 3.切换到root用户 su:Swith user(切换用户) su root 二、切换目录 目录结构:Linux 系…...
PLUS操作流程、应用与实践,多源不同分辨率数据的处理、ArcGIS的应用、PLUS模型的应用、InVEST模型的应用
PLUS模型是由中国地质大学(武汉)地理与信息工程学院高性能空间计算智能实验室开发,是一个基于栅格数据的可用于斑块尺度土地利用/土地覆盖(LULC)变化模拟的元胞自动机(CA)模型。PLUS模型集成了基于土地扩张分析的规则挖掘方法和基于多类型随机…...
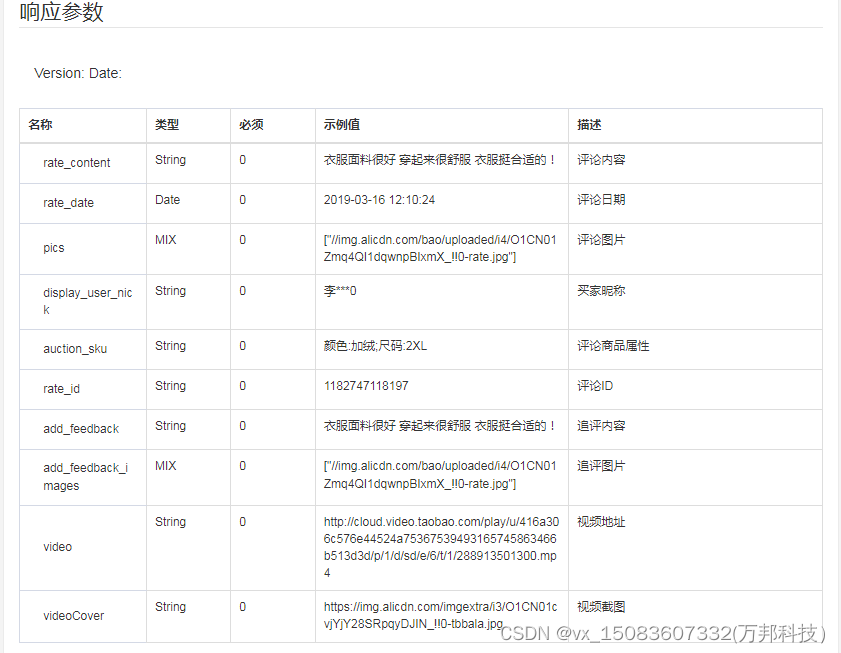
item_review-获得淘宝商品评论
一、接口参数说明: item_review-获得淘宝商品评论,点击更多API调试,请移步注册API账号点击获取测试key和secret 公共参数 请求地址: https://api-gw.onebound.cn/taobao/item_review 名称类型必须描述keyString是调用key(点击获…...
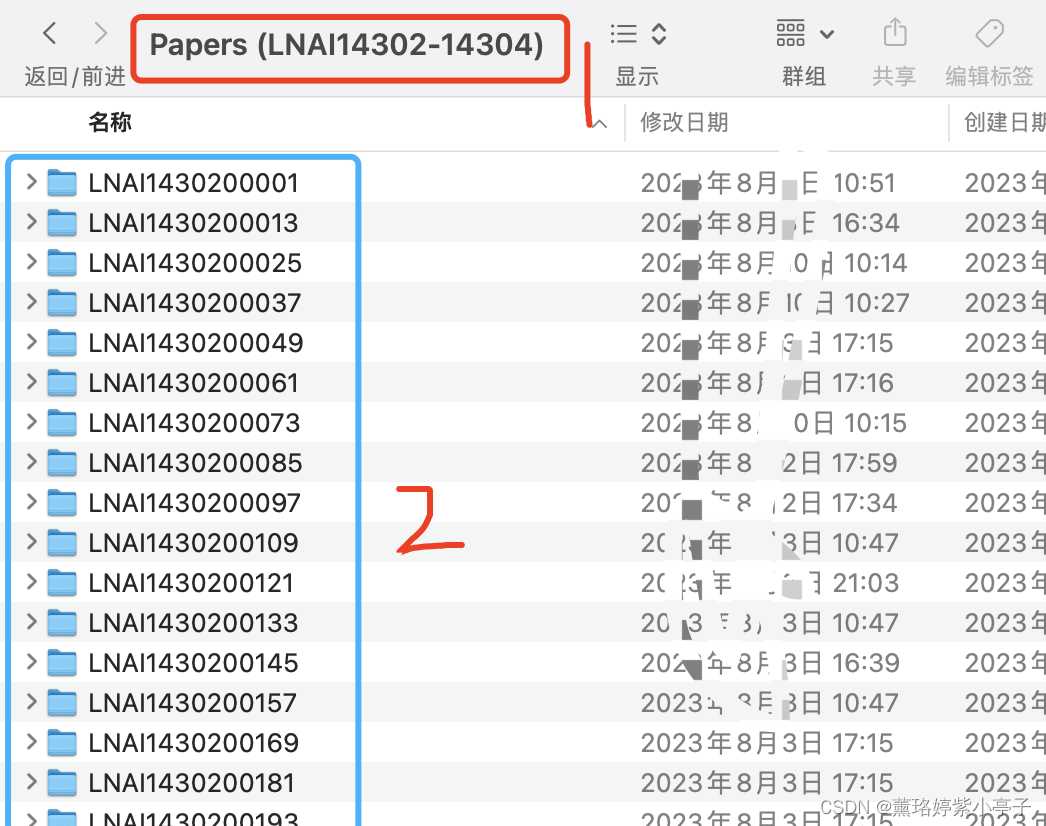
如何读取文件夹内的诸多文件,并选择性的保留部分文件
目录 问题描述: 问题解决: 问题描述: 当前有一个二级文件夹,第一层是文件夹名称是“Papers(LNAI14302-14304)",第二级文件夹目录名称如下图蓝色部分所示。第三层为存放的文件,如下下图所示,每一个文件中,均存放三个文件,分别为copyright.pdf, submission.pdf, s…...
每天一道leetcode:1129. 颜色交替的最短路径(图论中等广度优先遍历)
今日份题目: 给定一个整数 n,即有向图中的节点数,其中节点标记为 0 到 n - 1。图中的每条边为红色或者蓝色,并且可能存在自环或平行边。 给定两个数组 redEdges 和 blueEdges,其中: redEdges[i] [ai, bi…...
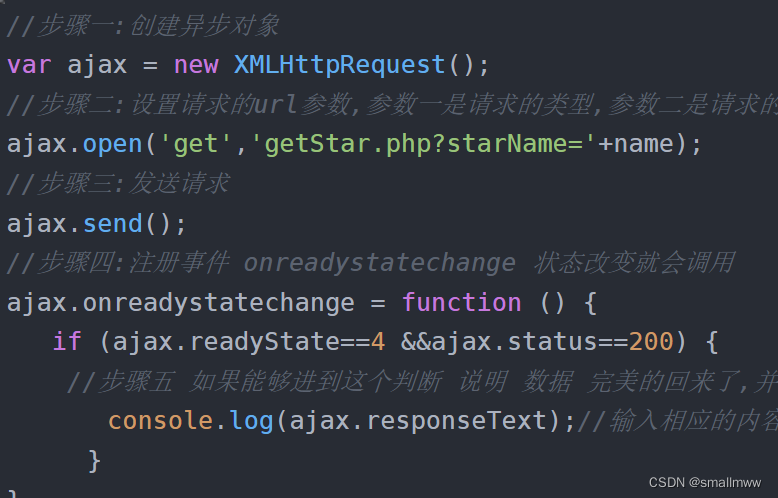
原生js发送ajax请求---ajax请求篇(一)
在原生js中我们使用的是XMLHttpRequest对象来发送ajax请求 主要步骤就是: 1.创建XMLHTTPRequest对象 2.使用open方法设置和服务器的交互信息 3.设置发送的数据,开始和服务器端交互 4.注册事件 5.更新界面 (1) get方式 //步骤一…...

【ARM 嵌入式 编译系列 2.1 -- GCC 编译参数学习】
文章目录 1.1 GCC 编译参数1.1.1 GCC arm-noe-eabi- 介绍1.1.1.1 ARM 和 Thumb 指令集区别1.1.2 GCC CFLAGS 介绍1.1.3 GCC LDFLAGS 介绍1.1.4 CXXFLAGS 介绍上篇文章:ARM 嵌入式 编译系列 2 – GCC 编译过程介绍 下篇文章:ARM 嵌入式 C 入门及渐进 3 – GCC attribute((weak…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
