第三章,矩阵,09-线性方程组解的判断与求法、矩阵方程
第三章,矩阵,09-线性方程组解的判断与求法、矩阵方程
- 定理
- 推论1
- 推论2
- 推论3
- 推论4
- 矩阵方程AX=B
- 解法
- 解的存在性
- 推论
玩转线性代数(21)线性方程组解的判断与求法的笔记,相关证明以及例子见原文
定理
对n元线性方程组 A x = b Ax=b Ax=b,A为系数矩阵, B = ( A ∣ b ) B=(A|b) B=(A∣b)为增广矩阵,则有
(1) A x = b Ax=b Ax=b无解 ⇔ R ( A ) < R ( A , b ) \Leftrightarrow R(A)\lt R(A,b) ⇔R(A)<R(A,b);
(2) A x = b Ax=b Ax=b有唯一解 ⇔ R ( A ) = R ( A , b ) = n \Leftrightarrow R(A)=R(A,b)=n ⇔R(A)=R(A,b)=n;
(3) A x = b Ax=b Ax=b有无穷多解 ⇔ R ( A ) = R ( A , b ) < n \Leftrightarrow R(A)= R(A,b)\lt n ⇔R(A)=R(A,b)<n.
推论1
对n元线性方程组 A x = b Ax=b Ax=b,A为系数矩阵, B = ( A ∣ b ) B=(A|b) B=(A∣b)为增广矩阵,则有
(1) A x = b Ax=b Ax=b无解 ⇔ R ( A ) < R ( A , b ) \Leftrightarrow R(A)\lt R(A,b) ⇔R(A)<R(A,b);
(2) A x = b Ax=b Ax=b有解 ⇔ R ( A ) = R ( A , b ) \Leftrightarrow R(A)=R(A,b) ⇔R(A)=R(A,b).
推论2
对n元线性方程组 A x = b Ax=b Ax=b,A为系数矩阵,或A为方阵,则有:
(1) A x = b Ax=b Ax=b有唯一解 ⇔ R ( A ) = n ⇔ ∣ A ∣ ≠ 0 \Leftrightarrow R(A)=n\Leftrightarrow |A|\neq 0 ⇔R(A)=n⇔∣A∣=0,其解为 x = A − 1 b x=A^{-1}b x=A−1b; ( R ( A ) = R ( B ) = n R(A)=R(B)=n R(A)=R(B)=n);
(2) ∣ A ∣ = 0 ⇔ |A|=0\Leftrightarrow ∣A∣=0⇔有无穷多解或无解.
推论3
对n元线性方程组 A x = 0 Ax=0 Ax=0,A为系数矩阵,方程必有零解,故不存在无解的情况,另外增广矩阵的最后一列为零,故其秩与系数矩阵A相同。
(1) A x = 0 Ax=0 Ax=0只有零解 ⇔ R ( A ) = n \Leftrightarrow R(A)=n ⇔R(A)=n;
(2) A x = 0 Ax=0 Ax=0有非零解 ⇔ R ( A ) < n \Leftrightarrow R(A)\lt n ⇔R(A)<n.
如果推论3中的A为方阵,则又有如下结论:
推论4
对n元线性方程组 A x = 0 Ax=0 Ax=0,A为系数矩阵且为方阵,则有
(1) A x = 0 Ax=0 Ax=0只有零解 ⇔ R ( A ) = n ⇔ ∣ A ∣ ≠ 0 \Leftrightarrow R(A)=n \Leftrightarrow |A| \neq 0 ⇔R(A)=n⇔∣A∣=0;
(2) A x = 0 Ax=0 Ax=0有非零解 ⇔ R ( A ) < n ⇔ ∣ A ∣ = 0 \Leftrightarrow R(A) \lt n \Leftrightarrow |A| = 0 ⇔R(A)<n⇔∣A∣=0.
矩阵方程AX=B
解法
若A是方阵,先确定A是否可逆,若A可逆,则有唯一解 X = A − 1 B X=A^{-1}B X=A−1B
若A不是方阵或不可逆,这时需要用待定元素法来求解。设未知矩阵X的元素为 x i j x_{ij} xij,即 X = ( x i j ) X=(x_{ij}) X=(xij),然后根据所给的矩阵方程列出 x i j x_{ij} xij所满足的线性方程组,通过解线性方程组求出所有元素 x i j x_{ij} xij,从而得到X.
解的存在性
设A为m * n矩阵,X为n * l矩阵,则B为m * l矩阵,把X和B按列分块,记为
X = ( x 1 , x 2 , . . . , x l ) , B = ( b 1 , b 2 , . . . b l ) X=(x_1,x_2,...,x_l), B=(b_1,b_2,...b_l) X=(x1,x2,...,xl),B=(b1,b2,...bl),
则矩阵方程 A X = B AX=B AX=B等价于l个向量方程
A x i = b i , ( i = 1 , 2 , . . . l ) Ax_i=b_i, (i=1,2,...l) Axi=bi,(i=1,2,...l),
又设 R ( A ) = r R(A)=r R(A)=r,且A的行最简形矩阵为 A ~ \tilde{A} A~,则 A ~ \tilde{A} A~一定有r个非零行。
再设 ( A , B ) = ( A , b 1 , b 2 , . . . , b i ) ∼ r ( A ~ , b ~ 1 , b ~ 2 , . . . , b ~ l ) (A,B)=(A, b_1, b_2,..., b_i)_{\sim}^r (\tilde{A}, \tilde{b}_1, \tilde{b}_2, ..., \tilde{b}_l) (A,B)=(A,b1,b2,...,bi)∼r(A~,b~1,b~2,...,b~l)
从而 ( A , b i ) r ∼ ( A ~ , b ~ i ) , ( i = 1 , 2 , . . . , l ) (A,b_i)_r^{\sim}(\tilde{A}, \tilde{b}_i), (i=1,2,...,l) (A,bi)r∼(A~,b~i),(i=1,2,...,l)
则 A X = B AX=B AX=B有解
⇔ \Leftrightarrow ⇔ A x i = b i Ax_i=b_i Axi=bi有解, ( i = 1 , 2 , . . . , l ) (i=1,2,...,l) (i=1,2,...,l)
⇔ \Leftrightarrow ⇔ R ( A ) = R ( A , b i ) , ( i = 1 , 2 , . . . , l ) R(A)=R(A,b_i), (i=1,2,...,l) R(A)=R(A,bi),(i=1,2,...,l)
⇔ \Leftrightarrow ⇔将 ( A , b i ) (A,b_i) (A,bi)化为行最简形 ( A ~ , b ~ i ) (\tilde{A}, \tilde{b}_i) (A~,b~i),此时 b ~ i \tilde{b}_i b~i的后m-r行全为零, ( i = 1 , 2 , . . . , l ) (i=1,2,...,l) (i=1,2,...,l).
⇔ \Leftrightarrow ⇔ ( A ~ , b ~ 1 , b ~ 2 , . . . , b ~ l ) (\tilde{A}, \tilde{b}_1, \tilde{b}_2, ..., \tilde{b}_l) (A~,b~1,b~2,...,b~l)的后m-r行全为零,
⇔ \Leftrightarrow ⇔ R ( A ) = R ( A , B ) R(A)=R(A,B) R(A)=R(A,B).
推论
设 A B = C AB=C AB=C,则 R ( C ) ≤ m i n { R ( A ) , R ( B ) } R(C)\leq min \{R(A), R(B) \} R(C)≤min{R(A),R(B)}
证明:
∵ A B = C , ∴ A X = B \because AB=C, \therefore AX=B ∵AB=C,∴AX=B有解 ⇒ R ( A ) = R ( A , C ) ≥ R ( C ) \Rightarrow R(A)=R(A, C) \geq R(C) ⇒R(A)=R(A,C)≥R(C)
又 B T A T = C T ∴ B T X = C T B^TA^T=C^T \therefore B^TX=C^T BTAT=CT∴BTX=CT有解 ⇒ R ( B ) = R ( B T ) = R ( B T , c T ) ≥ R ( C T ) = R ( C ) \Rightarrow R(B)=R(B^T)=R(B^T, c^T) \geq R(C^T)=R(C) ⇒R(B)=R(BT)=R(BT,cT)≥R(CT)=R(C)
∴ R ( C ) ≤ m i n { R ( A ) , R ( B ) } \therefore R(C) \leq min\{R(A), R(B)\} ∴R(C)≤min{R(A),R(B)}.
相关文章:

第三章,矩阵,09-线性方程组解的判断与求法、矩阵方程
第三章,矩阵,09-线性方程组解的判断与求法、矩阵方程 定理推论1推论2推论3推论4 矩阵方程AXB解法解的存在性推论 玩转线性代数(21)线性方程组解的判断与求法的笔记,相关证明以及例子见原文 定理 对n元线性方程组 A x b Axb Axb,…...
Vue-4.编译器VsCode
准备 Vue-1.零基础学习Vue Vue-2.nodejs的介绍和安装 Vue-3.vue简介 为什么用VsCode VsCode 是Vue官网首推的编译器它是完全免费的 下载安装VsCode 下载地址 安装的时候不停地下一步直到完成即可 安装插件 安装汉化插件 要将 Visual Studio Code(VSCode&am…...

Neo4j之Aggregation基础
在 Neo4j 中,聚合(Aggregation)是对数据进行计算、汇总和统计的过程。以下是一些使用聚合函数的常见例子,以及它们的解释: 计算节点数量: MATCH (p:Person) RETURN count(p) AS totalPersons;这个查询会计…...

Python 函数
Built-in Functions — Python 3.11.4 documentation...
Spring(三):Spring中Bean的生命周期和作用域
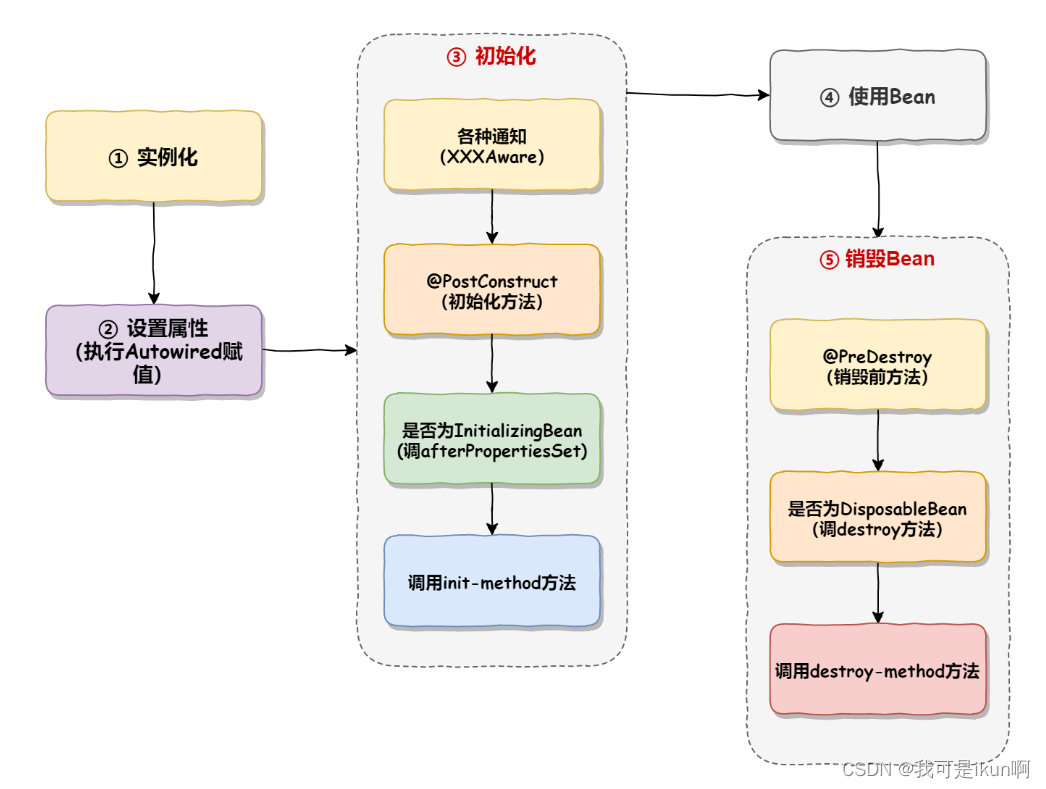
前言 在 Spring 中,那些组成应用程序的主体及由 Spring IOC 容器所管理的对象,被称之为 bean。简单地讲,bean 就是由 IOC 容器初始化、装配及管理的对象,除此之外,bean 就与应用程序中的其他对象没有什么区别了。而 b…...

【AutoLayout案例03-设置底部按钮之间相同间距 Objective-C语言】
一、好,咱们继续啊 1.咱们继续把autoLayout介绍一下 咱们的自动布局 给大家介绍一下 那么,自动布局呢 继续咱们给大家做的案例 做几个例子 把这几个例子做完以后 我们再给它 我们再给大家说一下,如何通过代码,来实现自动布局 虽然说,通过代码来实现自动布局,并不推荐 但…...

代码随想录算法训练营20期|第七天|哈希表part02|454.四数相加II ● 383. 赎金信 ● 15. 三数之和 ● 18. 四数之和 ● 总结
454.四数相加II 比较巧思的解法,先把nums1 和nums2的数两两相加,并存储sum和次数 再在nums3和nums4里找对应和sum和为0的数值i,j Time: N^2 Space:N^2, 最坏情况下A和B的值各不相同,相加产生的数字个数为 n^2 class Solution {public int fo…...
NavMeshPlus 2D寻路插件
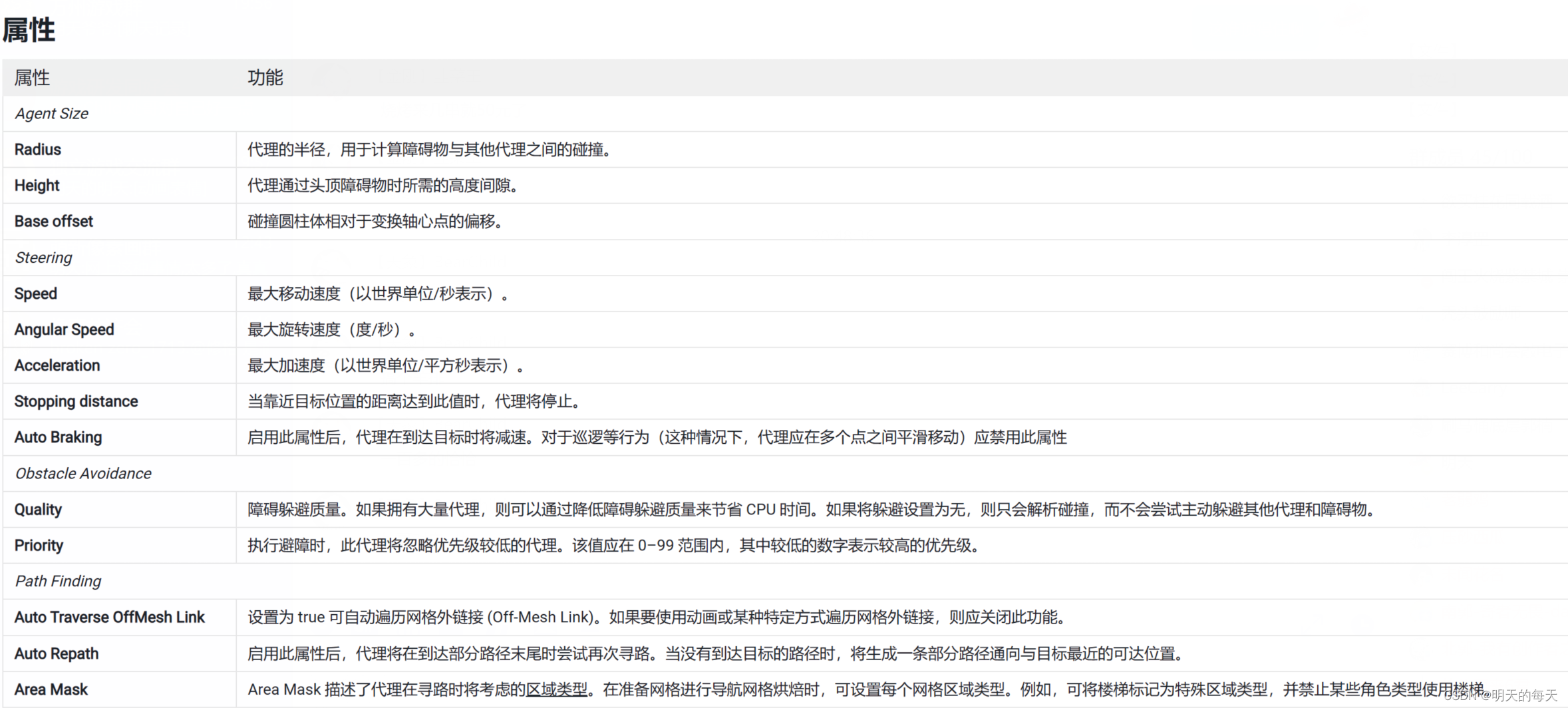
插件地址:h8man/NavMeshPlus: Unity NavMesh 2D Pathfinding (github.com) 我对Unity官方是深恶痛觉,一个2D寻路至今都没想解决,这破引擎早点倒闭算了. 这插件是githun的开源项目,我本身是有写jps寻路的,但是无法解决多个单位互相阻挡的问题(可以解决但是有性能问…...

【03】基础知识:typescript中的函数
一、typescript 中定义函数的方法 函数声明法 function test1(): string {return 返回类型为string }function test2(): void {console.log(没有返回值的方法) }函数表达式/匿名函数 const test3 function(): number {return 1 }二、typescript 中 函数参数写法 1、typesc…...
ssm社区文化宣传网站源码和论文
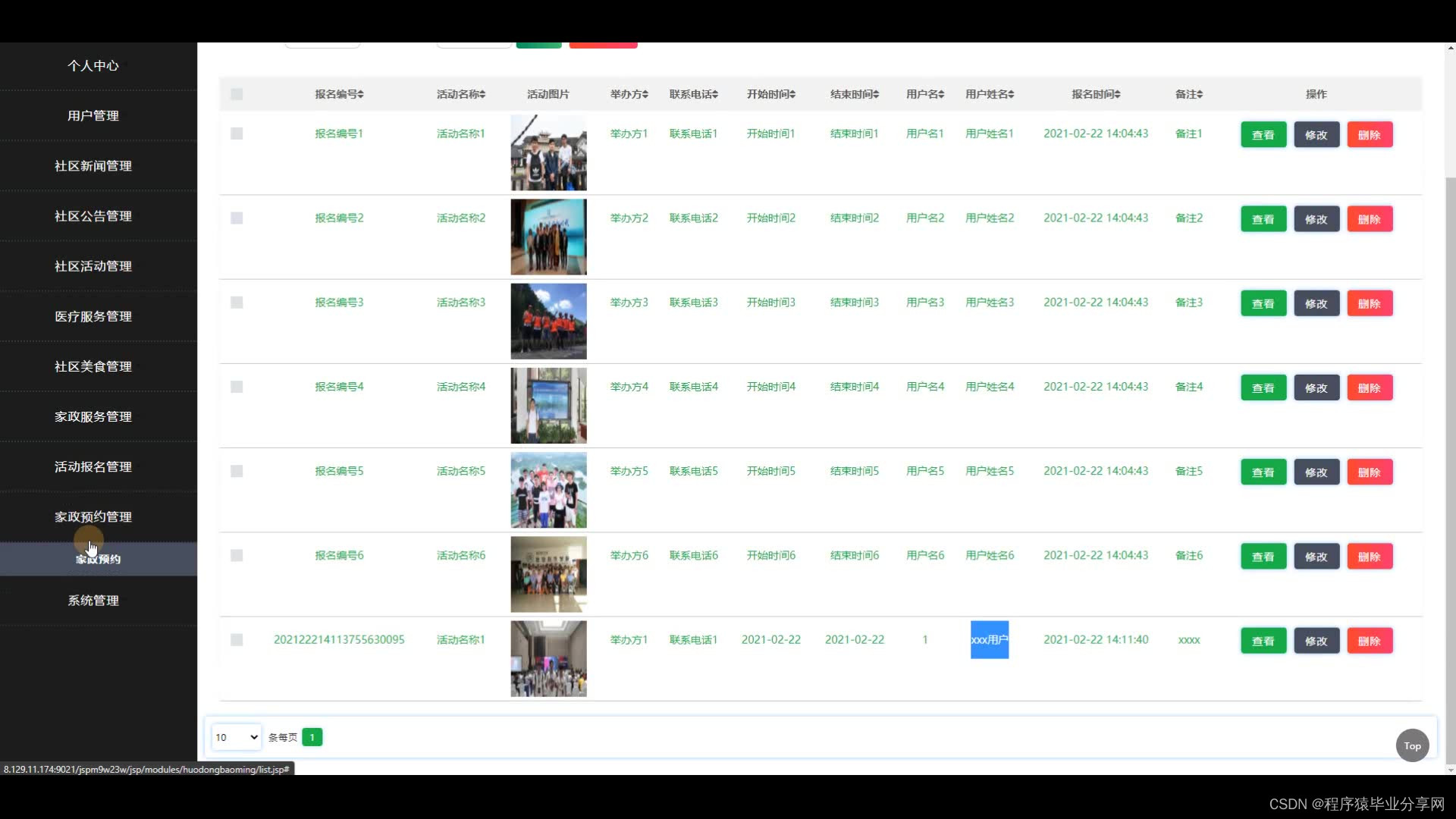
ssm社区文化宣传网站源码和论文019 开发工具:idea 数据库mysql5.7 数据库链接工具:navcat,小海豚等 技术:ssm 研究或设计的目的和意义: (一)研究目的: 通过本次课题能够将所学的Java编程知识以及Mysql数据库知…...

Go语言工程实践之测试与Gin项目实践
Go 语言并发编程 及 进阶与依赖管理_软工菜鸡的博客-CSDN博客 03 测试 回归测试一般是QA(质量保证)同学手动通过终端回归一些固定的主流程场景 集成测试是对系统功能维度做测试验证,通过服务暴露的某个接口,进行自动化测试 而单元测试开发阶段,开发者对单独的函数…...

排查docker无法启动问题
查看Linux系统操作日志(最后200行就可以排查): tail -200f /var/log/messages...

[C++ 网络协议] 套接字和地址族、数据序列
目录 1. 套接字 1.1 在Linux平台下构建套接字 1.1.1 用于接听的套接字(服务器端套接字) 1.1.2 用于发送请求的套接字(客户端套接字) 1.2 在Windows平台下构建套接字 1.2.1 Winsock的初始化 1.2.2 用于接听的套接字(服务器端套接字) 1.2.3 用于发送请求的套接字(客户端套…...

AI 绘画Stable Diffusion 研究(八)sd采样方法详解
大家好,我是风雨无阻。 本文适合人群: 希望了解stable Diffusion WebUI中提供的Sampler究竟有什么不同,想知道如何选用合适采样器以进一步提高出图质量的朋友。 想要进一步了解AI绘图基本原理的朋友。 对stable diffusion AI绘图感兴趣的朋…...

线程池满了如何处理
某天搬砖时遇到一个问题,我创建了一个线程池执行任务,刚开始的时候还是一切,结果第二天发现有些任务没有正常执行。一看日志才发现是高峰期时线程池给我占用慢了,任务被丢掉了。 举个例子,我创建了一个线程池&#…...
Java多线程编程中的线程间通信
Java多线程编程中的线程间通信 基本概念: 线程间通信是多线程编程中的一个重要概念,指的是不同线程之间如何协调和交换信息,以达到共同完成任务的目的。 线程间通信的目的 是确保多个线程能够按照一定的顺序和规则进行协作ÿ…...

write javaBean error, fastjson version 1.2.76
fastjson JSON.toJSONString 报错: > [0] JavaBeanSerializer.java->541: com.alibaba.fastjson.serializer.JavaBeanSerializer->write()> [1] JavaBeanSerializer.java->154: com.alibaba.fastjson.serializer.JavaBeanSerializer->write()>…...
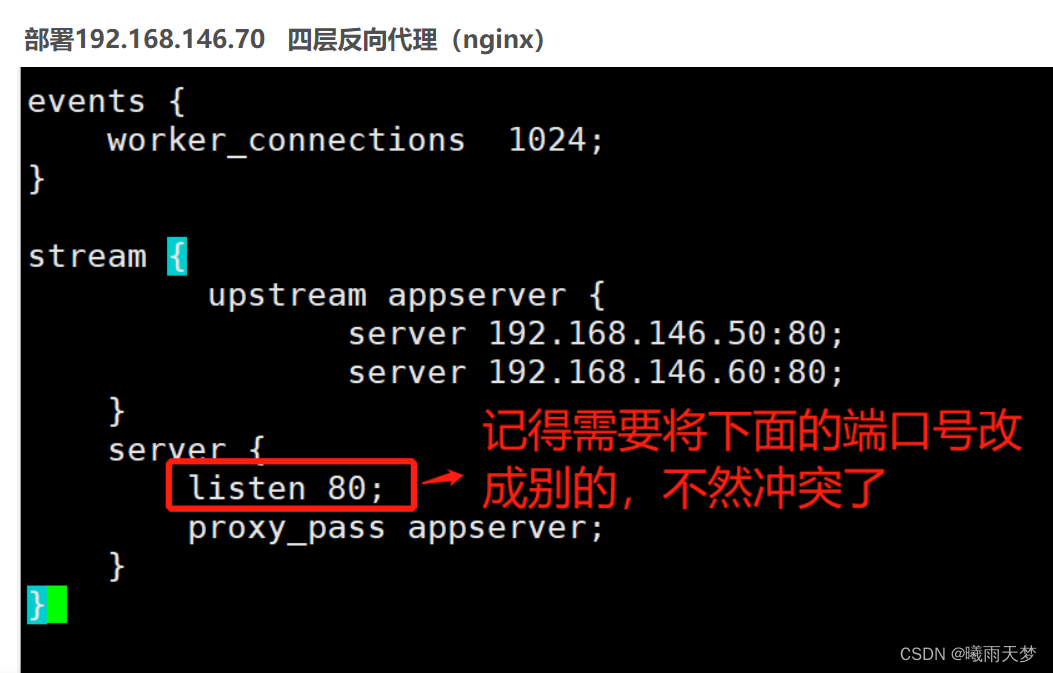
Tomcat的部署及优化(多实例和动静分离)
目录 绪论 1、tomact 1.1 核心组件 1.2 什么是 servlet 1.3 什么是 JSP? 1.4 Tomcat 功能组件结构 1.5 Tomcat 请求过程 2、Tomcat 服务部署 2.1 tomcat自身优化: 2.2 内核优化 2.3 jvm 2.3.1 jvm配置 2.3.2 Tomcat配置JVM参数 2.3.3 jvm优化 3、tom…...

品牌推广革新之道:海外网红与内容营销的融合
随着数字时代的来临,品牌推广的方式正在经历着革命性的变化。传统的广告手段逐渐失去了吸引力,而内容营销正成为品牌推广的新宠儿。尤其是海外网红的崛起,不仅改变了推广方式,更重新定义了品牌与消费者之间的互动关系。本文Nox聚星…...

【 BERTopic应用 02/3】 分析卡塔尔世界杯推特数据
摄影:Fauzan Saari on Unsplash 一、说明 这是我们对世界杯推特数据分析的第3部分,我们放弃了。我们将对我们的数据进行情绪分析,以了解人们对卡塔尔世界杯的感受。我将在这里介绍的一个功能强大的工具包是Hugging Face,您可以在…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
