代码随想录第四十八天
代码随想录第四十八天
- Leetcode 198. 打家劫舍I
- Leetcode 213. 打家劫舍 II
- Leetcode 337. 打家劫舍 III
Leetcode 198. 打家劫舍I
题目链接: 打家劫舍I
自己的思路:想不太出来递推公式!!!!
正确思路:这个题主要是看是否偷第下标为i的房间;直接动规五部曲:1、dp数组的含义:dp[i]表示从下标0到下标i(包括下标i,但不一定偷下标i)所能偷到的最大金钱数;2、递推公式:分为偷下标i和不偷下标i,如果偷下标i的话,那么0-i的最大金钱数就是之前偷的最大金钱数也就是dp[i-2],因为没法偷下标为i-1的房间;那么当不偷下标i的话,那么0-i的最大金钱数就是dp[i-1]了,两者中取最大值;3、dp数组初始化:由于当前的最大金钱和前面两个状态有关,所以所有的值一定是和dp[0]和dp[1]有关,dp[0]表示0-0的最大金钱,所以一定选下标为0的房间,dp[1]是0-1的最大金钱,所以只能选一个,选最大者即可;4、遍历顺序:由于是找包含最后一个房间的最大金钱,所以一定要从前向后遍历才可以!5、打印dp数组:主要用于debug!!!!
代码:
class Solution {public int rob(int[] nums) {if (nums.length==1) return nums[0];if (nums.length==2) return Math.max(nums[0],nums[1]);int[] dp = new int[nums.length];//初始化dp[0] = nums[0];dp[1] = Math.max(nums[0],nums[1]);for (int i =2;i<nums.length;i++){//递推公式(偷第i天和不偷第i天)//从小到大遍历dp[i] = Math.max(dp[i-2]+nums[i],dp[i-1]);}return dp[nums.length-1];}
}
Leetcode 213. 打家劫舍 II
题目链接: 打家劫舍 II
自己的思路:不好处理环的问题!!!
正确思路:将环的问题处理成两个子问题:一个是不考虑最后一间房间,一个是不考虑第一间房间,然后根据这两种线性情况求最大值,线性情况就是打家劫舍一的情况,这里我们对打家劫舍一的代码做了优化,使用三个变量来代替原来的dp数组!!!!
代码:
class Solution {public int rob(int[] nums) {int len = nums.length;if (len==1) return nums[0];//两种情况取最大值return Math.max(robaction(Arrays.copyOfRange(nums,0,nums.length-1)),robaction(Arrays.copyOfRange(nums,1,nums.length)));}//打家劫舍一的代码简化版public int robaction(int[] nums){int x=0,z=0,y;for (int num:nums){y = z;z = Math.max(x+num,y);x = y;}return z;}
}
Leetcode 337. 打家劫舍 III
题目链接: 打家劫舍 III
自己的思路:好难!!!!
正确思路:树形dp没接触过,完全没有思路!!!这道题要使用后序遍历来递归二叉树,因为我们要求左右子树所能偷到的最多的钱,然后再求中间节点所能偷到最多的钱,一次次向上递归,最后返回给根节点!递归三部曲:1、递归参数和返回值:递归参数就是当前节点,返回值是一个维度为2的一维数组res(这里我们选择res[0]表示偷当前节点,res[1]表示不偷当前节点);2、终止条件:当当前节点为null时,直接返回全为0的一维数组即可!3、单层逻辑:这里我们拿一点节点来说明:当偷当前结点的房间时,那么一定不能偷左右孩子的房间,val=node.val+left[1]+right[1];当不偷当前结点的房间时,我们要分情况进行讨论,因为我们不一定必须偷左右孩子的房间,我们要从中选择最大值来判断,所以val=max(left[0],left[1])+max(right[0],right[1]),然后将这两个数组成一维数组返回即可!!!!
代码:
class Solution {public int rob(TreeNode root) {//索引0表示偷 索引1表示不偷int[] res = robac(root);return Math.max(res[0],res[1]);}public int[] robac(TreeNode node){if (node==null) return new int[2];int[] left = robac(node.left);int[] right = robac(node.right);//偷当前结点int val1 = node.val + left[1]+right[1];//不偷当前节点int val2 = Math.max(left[0],left[1])+Math.max(right[0],right[1]);return new int[]{val1,val2};}
}
相关文章:

代码随想录第四十八天
代码随想录第四十八天 Leetcode 198. 打家劫舍ILeetcode 213. 打家劫舍 IILeetcode 337. 打家劫舍 III Leetcode 198. 打家劫舍I 题目链接: 打家劫舍I 自己的思路:想不太出来递推公式!!!! 正确思路:这个题主要是看是否偷第下标为…...
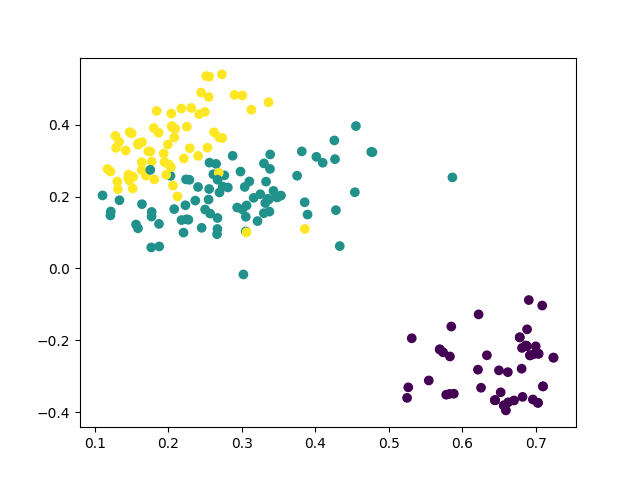
书写自动智慧:探索Python文本分类器的开发与应用:支持二分类、多分类、多标签分类、多层级分类和Kmeans聚类
书写自动智慧:探索Python文本分类器的开发与应用:支持二分类、多分类、多标签分类、多层级分类和Kmeans聚类 文本分类器,提供多种文本分类和聚类算法,支持句子和文档级的文本分类任务,支持二分类、多分类、多标签分类…...
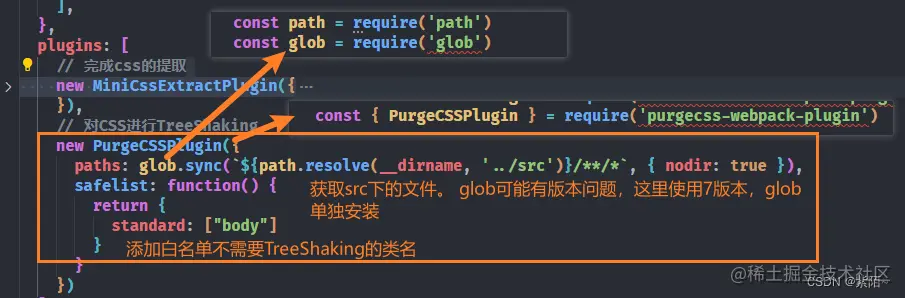
前端Webpack面试题
1.说说你对webpack的理解 开发时,我们会使用框架 (React、Vue) ,ES6 模块化语法,Less/Sass 等 CSS 预处理器等语法进行开发,这样的代码要想在浏览器运行必须经过编译成浏览器能识别的 JS、CSS语法才能运行。所以我们需要打包工…...

LabVIEW使用边缘检测技术实现彩色图像隐写术
LabVIEW使用边缘检测技术实现彩色图像隐写术 隐写术是隐藏信息的做法,以隐瞒通信的存在而闻名。该技术涉及在适当的载体(如图像,音频或视频)中插入秘密消息。在这些载体中,数字图像因其在互联网上的广泛使用而受到青睐…...

第一次参加计算机会议报告注意事项以及心得
计算机会议参会报告 注意事项参会前参会中参会后 参会心得 注意事项 接下来的会议注意事项分为:(1)参会前,(2)参会中,(3)参会后 参会前 参会前,一般被邀请…...
基础语法与基础类型)
TypeScript教程(二)基础语法与基础类型
一、基础语法 TypeScript由以下几个部分组成 1.模块 2.函数 3.变量 4.语句和表达式 5.注释 示例: Runoob.ts 文件代码: const hello : string "Hello World!" console.log(hello) 以上代码首先通过 tsc 命令编译: tsc …...

问道管理:网上如何打新股?
随着资本市场的不断敞开,越来越多的人开始重视股票市场,并想经过网上打新股来取得更大的出资收益。但是,网上打新股的办法并不简略,怎样才能成功地打新股呢?本文将从多个角度剖析,协助广阔出资者处理这一问…...

重磅更新,HertzBeat 集群版发布,易用友好的开源实时监控系统!
什么是 HertzBeat? HertzBeat 赫兹跳动 是一个拥有强大自定义监控能力,高性能集群,无需 Agent 的开源实时监控告警系统。 特点 集 监控告警通知 为一体,支持对应用服务,数据库,操作系统,中间件…...

.NET6使用微信小程序授权登录,获取手机号
1.在appsettings配置你的小程序配置信息 //微信小程序信息配置"WechatConfig": {"appid": "", //小程序ID"secret": "" //小程序秘钥},2.请求接口时先获取Access_token #region 获取小程序的Access_tokenpublic object GetA…...

游戏类APP如何提升用户的活跃度?
移动游戏行业,追求使用率的营销能发挥强大的功效,可帮助减少玩家流失、追回流失的玩家、提高活跃玩家所带来的价值以及增加付费玩家贡献的收入。 一、了解玩家需求 想要提升玩家的活跃,首先要知道,玩家喜欢玩哪些平台的游戏&…...
)
【Sklearn】基于支持向量机算法的数据分类预测(Excel可直接替换数据)
【Sklearn】基于支持向量机算法的数据分类预测(Excel可直接替换数据) 1.模型原理1.1 数学模型1.2 模型原理2.模型参数3.文件结构4.Excel数据5.下载地址6.完整代码7.运行结果1.模型原理 支持向量机(Support Vector Machine,SVM)是一种用于分类和回归的监督学习算法,其基本…...

抽象类与接口
一,类 定义类 部分与ES6用法基本一致。通过class定义类名,并通过constructor定义构造函数,通过super关键字来调用父类的方法。 class Person {name: string; // 属性constructor(name: string) { // 构造函数this.name name;}eat()…...

第三章,矩阵,09-线性方程组解的判断与求法、矩阵方程
第三章,矩阵,09-线性方程组解的判断与求法、矩阵方程 定理推论1推论2推论3推论4 矩阵方程AXB解法解的存在性推论 玩转线性代数(21)线性方程组解的判断与求法的笔记,相关证明以及例子见原文 定理 对n元线性方程组 A x b Axb Axb,…...
Vue-4.编译器VsCode
准备 Vue-1.零基础学习Vue Vue-2.nodejs的介绍和安装 Vue-3.vue简介 为什么用VsCode VsCode 是Vue官网首推的编译器它是完全免费的 下载安装VsCode 下载地址 安装的时候不停地下一步直到完成即可 安装插件 安装汉化插件 要将 Visual Studio Code(VSCode&am…...

Neo4j之Aggregation基础
在 Neo4j 中,聚合(Aggregation)是对数据进行计算、汇总和统计的过程。以下是一些使用聚合函数的常见例子,以及它们的解释: 计算节点数量: MATCH (p:Person) RETURN count(p) AS totalPersons;这个查询会计…...

Python 函数
Built-in Functions — Python 3.11.4 documentation...
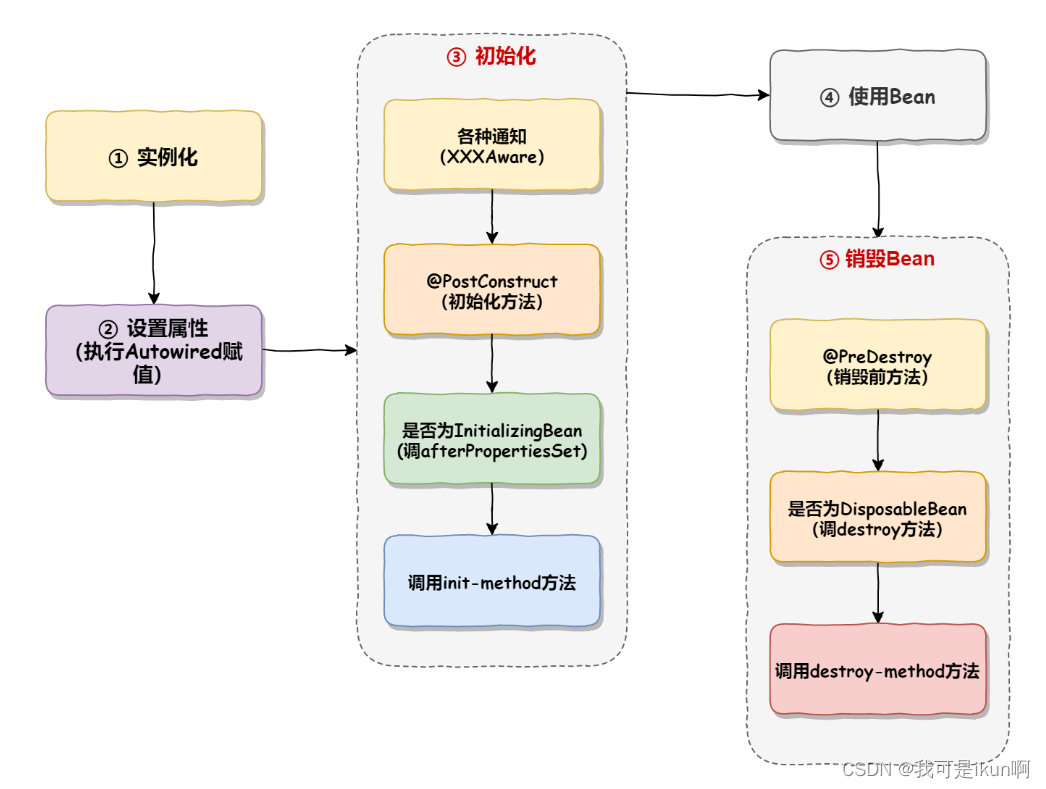
Spring(三):Spring中Bean的生命周期和作用域
前言 在 Spring 中,那些组成应用程序的主体及由 Spring IOC 容器所管理的对象,被称之为 bean。简单地讲,bean 就是由 IOC 容器初始化、装配及管理的对象,除此之外,bean 就与应用程序中的其他对象没有什么区别了。而 b…...

【AutoLayout案例03-设置底部按钮之间相同间距 Objective-C语言】
一、好,咱们继续啊 1.咱们继续把autoLayout介绍一下 咱们的自动布局 给大家介绍一下 那么,自动布局呢 继续咱们给大家做的案例 做几个例子 把这几个例子做完以后 我们再给它 我们再给大家说一下,如何通过代码,来实现自动布局 虽然说,通过代码来实现自动布局,并不推荐 但…...

代码随想录算法训练营20期|第七天|哈希表part02|454.四数相加II ● 383. 赎金信 ● 15. 三数之和 ● 18. 四数之和 ● 总结
454.四数相加II 比较巧思的解法,先把nums1 和nums2的数两两相加,并存储sum和次数 再在nums3和nums4里找对应和sum和为0的数值i,j Time: N^2 Space:N^2, 最坏情况下A和B的值各不相同,相加产生的数字个数为 n^2 class Solution {public int fo…...
NavMeshPlus 2D寻路插件
插件地址:h8man/NavMeshPlus: Unity NavMesh 2D Pathfinding (github.com) 我对Unity官方是深恶痛觉,一个2D寻路至今都没想解决,这破引擎早点倒闭算了. 这插件是githun的开源项目,我本身是有写jps寻路的,但是无法解决多个单位互相阻挡的问题(可以解决但是有性能问…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...
