【数学建模】--主成分分析
本讲将介绍主成分分析(Principal Component Analysis,PCA),主成分分析是一种降维算法,它能将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能反映出原始数据的大部分信息,一般来说,当研究的问题涉及到多变量且变量之间存在很强的相关性时,我们可以考虑使用主成分分析的方法来对数据进行简化。
(将多个指标转换为少数几个主成分)
问题的提出:
对于变量多,分析时难度大=>因此用较少新变量代替原来较多就变量。
数据降维的作用:
主成分分析的思想:


严谨的数学符号:

PCA的计算步骤(理论步骤):


案列1
计算关键变量:
一般看累积贡献率,一般选择累积贡献率较大且所选变量少时情况。如下图的累积贡献率到第三个时已经为85.9%,后面的已经相对增加的趋势较少说明后面变量的贡献率相对较少可以不用考虑。
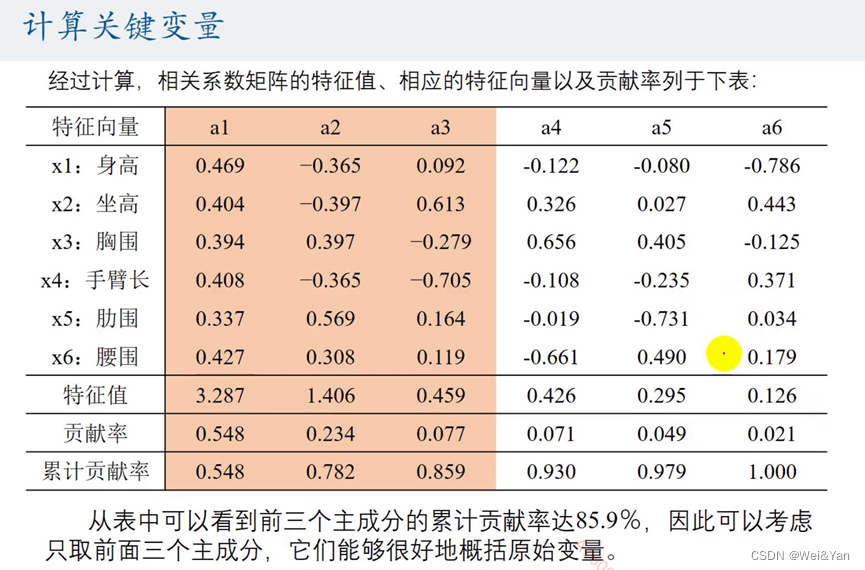
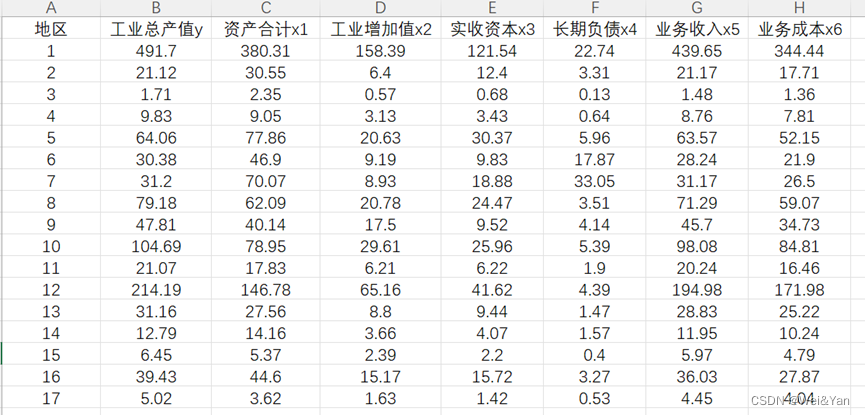
写出主成分并简要分析:
主成分分析的说明:
案例2:
计算关键变量: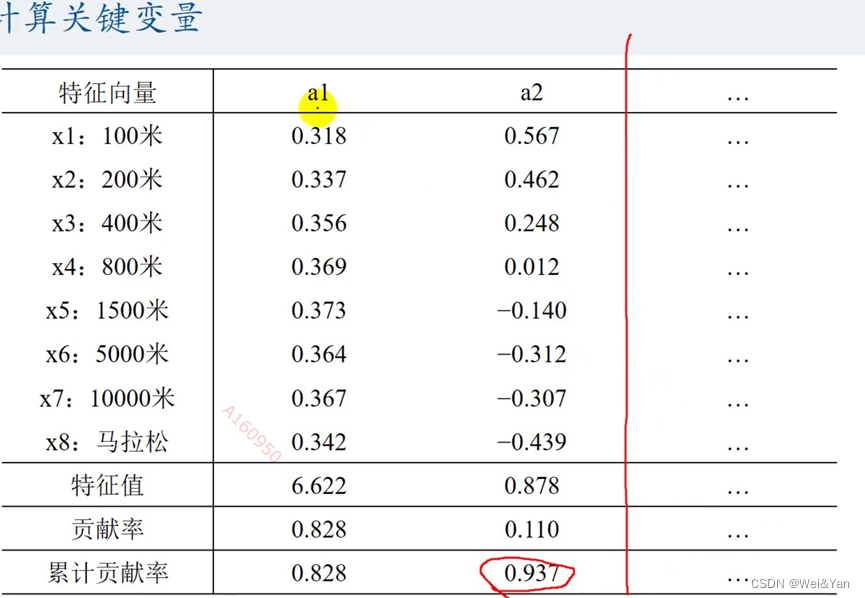
对主成分分析:
主成分分析的MATLAB代码实现:
- 标准化数据。利用函数zscore(数据)
- 计算标准化后样本的协方差。函数cov(标准化后数据)
补:在我们进行完1,2步后得到了样本相关系数矩阵,可对其相关系数进行可视化。
步骤:
a.复制相关系数矩阵->excel,调整表格的行高列宽。
b.色阶->三色表->管理规则->编辑规则->修改数字,范围->应用。

让我们继续回到matlab的操作:
3.根据PCA计算步骤,接下来计算R(相关系数矩阵)的特征值和特征向量。函数eig(R)。若eig不给返参数,默认只返回特征值。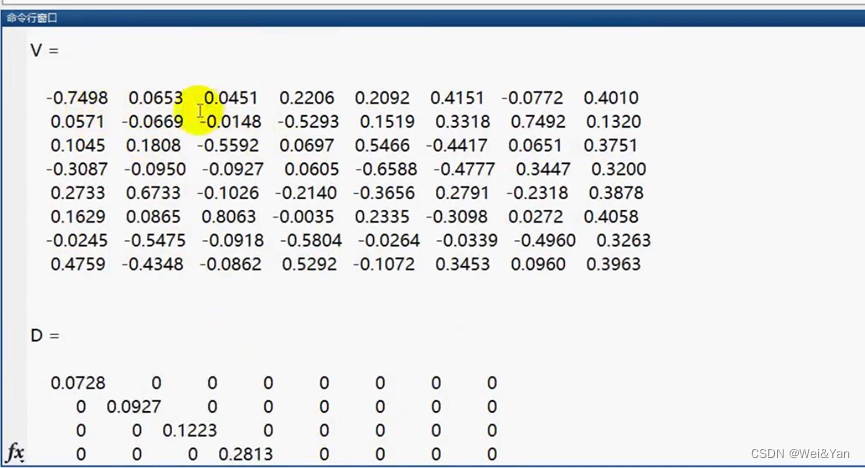
4.计算主成分贡献率和累积贡献率。(计算过程复杂,后期会有代码和注释的补充)
5.根据累积贡献率选择主成分变量的个数,并且进行主成分变量的计算。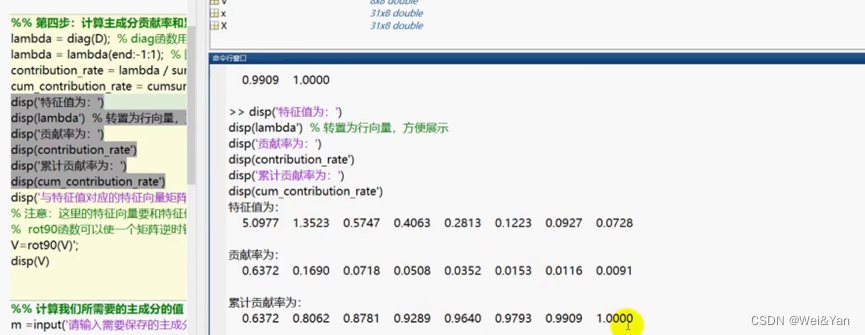
6.根据实际问题选择,如果为聚类模型则将数据复制到excel,再用spss解决;如果为主成分回归,则还需要计算标准化y值(利用函数zscore),再将得到的标准化y和主成分变量F1,F2……Fm复制到excel再导入到stata中进行分析。
Matlab进行主成分分析:
结果的解释:
主成分分析的滥用(了解):
对于聚类问题的主成分分析的使用:
将数据有导入spss中再进行聚类:
(关于聚类模型可以参考博主之前的一篇文章:【数学建模】--聚类模型_Wei&Yan的博客-CSDN博客)
分析-分类-系统聚类-导入重要变量-图-普系图-生成谱系图后根据普系图确定类的个数。
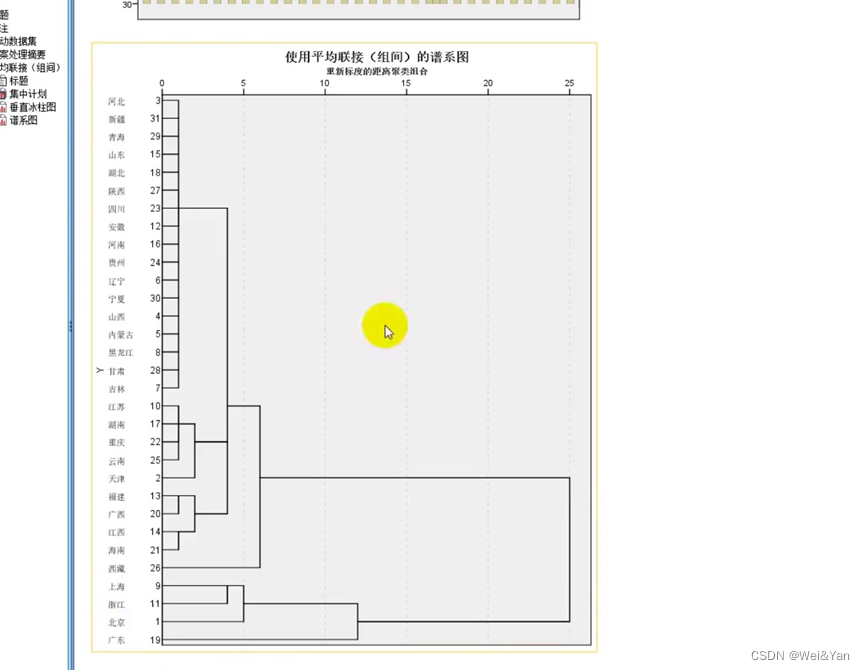
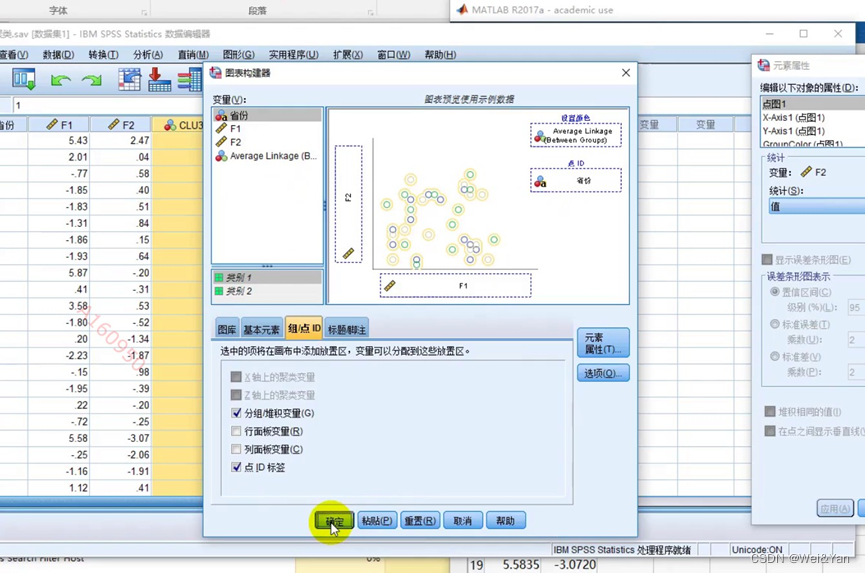
确定类的个数后再重新运行生成散点图:
(在确定类的个数后要手动输入)

Spss聚类: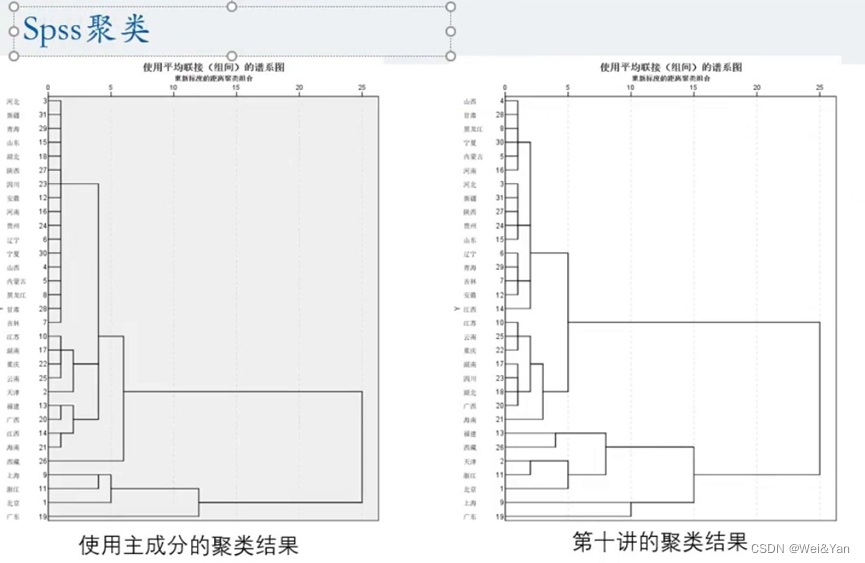
效果图:
主成分回归: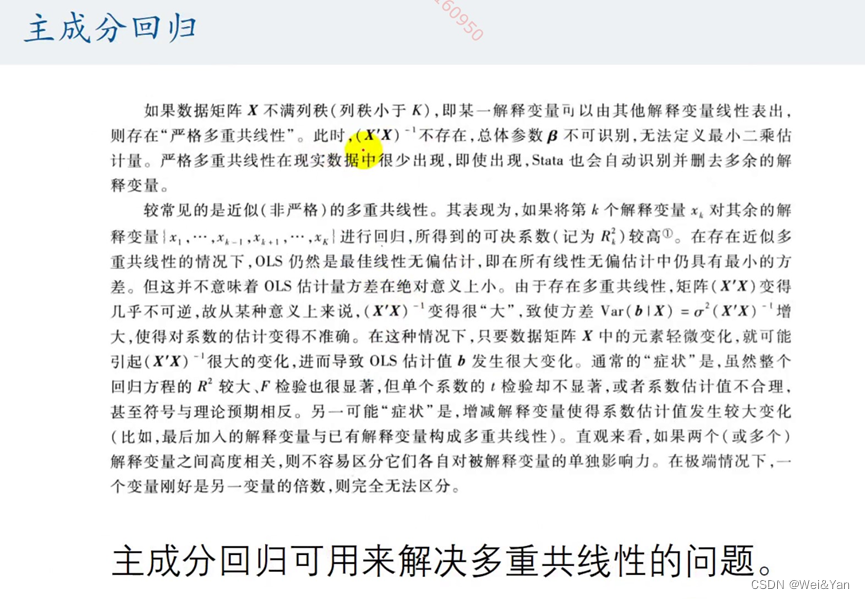
利用Stata来解决主成分回归:
关于主成分回归的看法:
课后作业:
如果不了解多元回归和stata的应用可参考博主的:数学建模—多元线性回归分析(+lasso回归的操作)_Wei&Yan的博客-CSDN博客
- 直接回归,并用异方差(estat imtest,white)和多重共线性检验(estat vif):
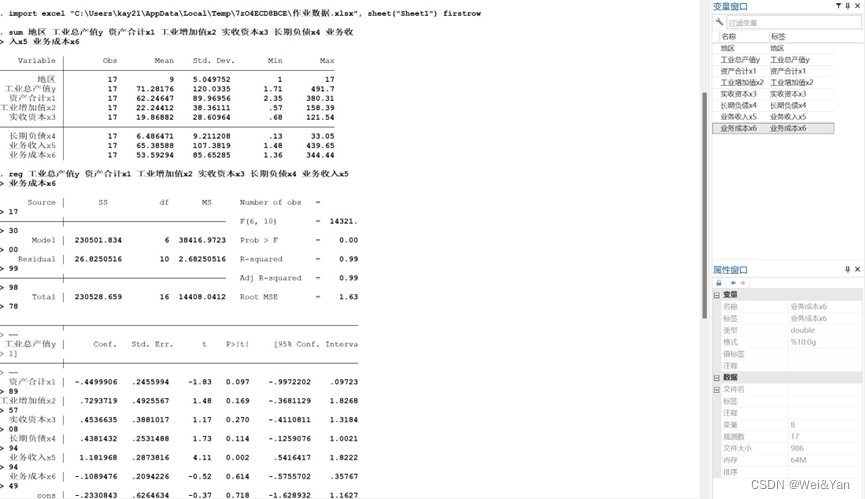

2.逐步回归分析(向后逐步):
3.主成分分析:
观察到前两项的累积贡献率已经较高,所以选择前两项为主成分自变量,得到了标准化后的主成分自变量F1,F2和Y。
将数据导出到excel再导入stata进行分析:
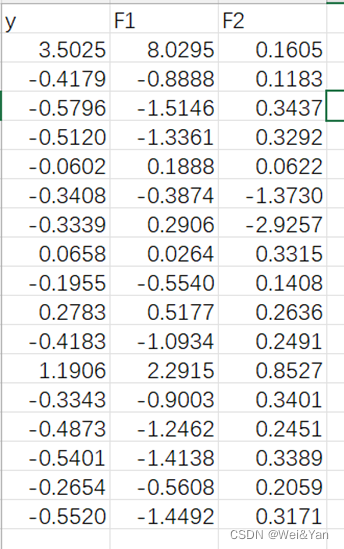
Stata运行结果:
MATLAB代码参考:
clear;clc% 主成分聚类% 主成分回归
load data3.mat%博主在作业测试中的数据。
% 注意,这里可以对数据先进行描述性统计
% 描述性统计的内容见第5讲.相关系数
[n,p] = size(x); % n是样本个数,p是指标个数%% 第一步:对数据x标准化为X
X=zscore(x); % matlab内置的标准化函数(x-mean(x))/std(x)%% 第二步:计算样本协方差矩阵
R = cov(X);%% 注意:以上两步可合并为下面一步:直接计算样本相关系数矩阵
R = corrcoef(x);
disp('样本相关系数矩阵为:')
disp(R)%% 第三步:计算R的特征值和特征向量
% 注意:R是半正定矩阵,所以其特征值不为负数
% R同时是对称矩阵,Matlab计算对称矩阵时,会将特征值按照从小到大排列哦
% eig函数的详解见第一讲层次分析法的视频
[V,D] = eig(R); % V 特征向量矩阵 D 特征值构成的对角矩阵%% 第四步:计算主成分贡献率和累计贡献率
lambda = diag(D); % diag函数用于得到一个矩阵的主对角线元素值(返回的是列向量)
lambda = lambda(end:-1:1); % 因为lambda向量是从小大到排序的,我们将其调个头
contribution_rate = lambda / sum(lambda); % 计算贡献率
cum_contribution_rate = cumsum(lambda)/ sum(lambda); % 计算累计贡献率 cumsum是求累加值的函数
disp('特征值为:')
disp(lambda') % 转置为行向量,方便展示
disp('贡献率为:')
disp(contribution_rate')
disp('累计贡献率为:')
disp(cum_contribution_rate')
disp('与特征值对应的特征向量矩阵为:')
% 注意:这里的特征向量要和特征值一一对应,之前特征值相当于颠倒过来了,因此特征向量的各列需要颠倒过来
% rot90函数可以使一个矩阵逆时针旋转90度,然后再转置,就可以实现将矩阵的列颠倒的效果
V=rot90(V)';
disp(V)%% 计算我们所需要的主成分的值
m =input('请输入需要保存的主成分的个数: ');
F = zeros(n,m); %初始化保存主成分的矩阵(每一列是一个主成分)
for i = 1:mai = V(:,i)'; % 将第i个特征向量取出,并转置为行向量Ai = repmat(ai,n,1); % 将这个行向量重复n次,构成一个n*p的矩阵F(:, i) = sum(Ai .* X, 2); % 注意,对标准化的数据求了权重后要计算每一行的和
end%% (1)主成分聚类 : 将主成分指标所在的F矩阵复制到Excel表格,然后再用Spss进行聚类
% 在Excel第一行输入指标名称(F1,F2, ..., Fm)
% 双击Matlab工作区的F,进入变量编辑中,然后复制里面的数据到Excel表格
% 导出数据之后,我们后续的分析就可以在Spss中进行。%%(2)主成分回归:将x使用主成分得到主成分指标,并将y标准化,接着导出到Excel,然后再使用Stata回归
%Y = zscore(y); % 一定要将y进行标准化哦~
% 在Excel第一行输入指标名称(Y,F1, F2, ..., Fm)
% 分别双击Matlab工作区的Y和F,进入变量编辑中,然后复制里面的数据到Excel表格
% 导出数据之后,我们后续的分析就可以在Stata中进行。相关文章:

【数学建模】--主成分分析
本讲将介绍主成分分析(Principal Component Analysis,PCA),主成分分析是一种降维算法,它能将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能…...

gitee(码云)如何生成并添加公钥,以及配置用户信息
一,简介 在使用Gitee的时候,公钥是必须的,无论是克隆还是上传。本文主要介绍如何本地生成和添加公钥到服务器,然后配置自己的用户信息,方便日后拉取与上传代码。 二,步骤介绍 2.1 本地生成公钥 打开git ba…...
)
wangeditor上传图片并展示在输入框内方法(vue3)
安装vue3组件 yarn add @wangeditor/editor-for-vue@next # 或者 npm install @wangeditor/editor-for-vue@next --save 页面中创建一个新的组件 <template><div style="border: 1px solid #ccc; text-align: left"><Toolbar style="border-…...
UGUI基础游戏对象Canvas
一.画布Canvas对象概述 画布是一种带有画布组件的游戏对象,所有 UI 元素都必须是此类画布的子项。 创建新的 UI 元素(如使用菜单 GameObject > UI > Image 创建图像)时,如果场景中还没有画布,则会自动创建画布。…...

PK Nounique CASCADE DROP INDEX keep index
Explicit Control Over Indexes when Creating, Disabling, or Dropping PK/Unique Constraints (Doc ID 139666.1)编辑To Bottom PURPOSEIn Oracle 9i, the DBA has an explicit control over how indexes are affectedwhile creating, disabling, or dropping Primary Ke…...

【Antd】实现Table组件行点击,解决某一列不触发行点击
今天有个新需求,点击table行,执行一些操作。实现过程中遇到了:点击操作列、操作列内按钮会冒泡触发行点击。antd版本:1.7.8 一、解决方案 customRow <a-table :customRow"handleClickRow" :data-source"data_li…...

Kafka3.0.0版本——Broker( 退役旧节点)示例
目录 一、服务器信息二、先启动4台zookeeper,再启动4台kafka三、通过PrettyZoo工具验证启动的kafka是否ok四、查看4台kafka集群节点上是否存在创建的名称为news的主题五、退役旧节点5.1、执行负载均衡操作5.2、 执行停止命令5.3、再次查看kafka中的创建过的名称为ne…...
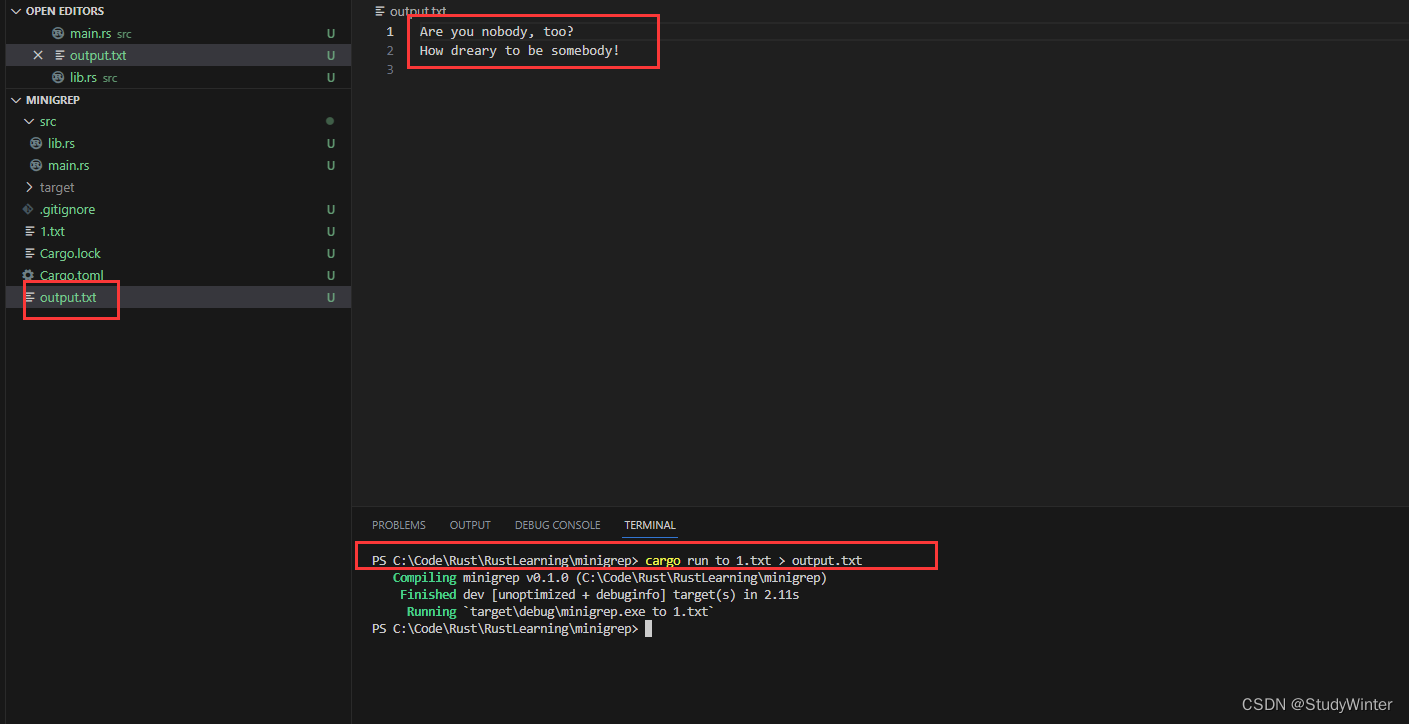
【Rust】Rust学习 第十二章一个 I/O 项目:构建一个命令行程序
本章既是一个目前所学的很多技能的概括,也是一个更多标准库功能的探索。我们将构建一个与文件和命令行输入/输出交互的命令行工具来练习现在一些你已经掌握的 Rust 技能。 Rust 的运行速度、安全性、单二进制文件输出和跨平台支持使其成为创建命令行程序的绝佳选择…...
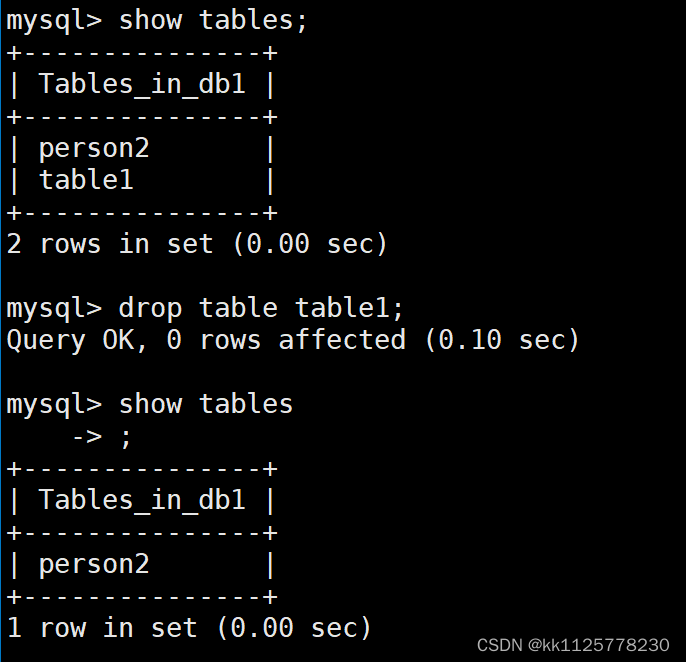
【MySQL--->表的操作】
文章目录 [TOC](文章目录) 一、创建表二、查看表三、修改表四、删除表drop table 表名;  一、创建表 语句格式:create table 表名(列名 类型,…)字符集 校验规则 存储引擎;字符集和校…...
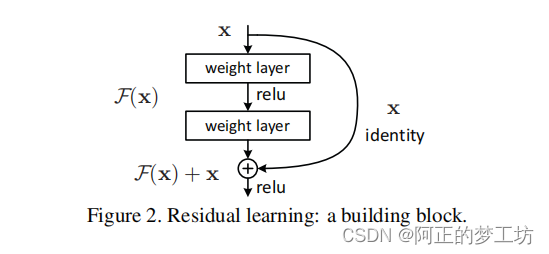
PyTorch从零开始实现ResNet
文章目录 代码实现参考 代码实现 本文实现 ResNet原论文 Deep Residual Learning for Image Recognition 中的50层,101层和152层残差连接。 代码中使用基础残差块这个概念,这里的基础残差块指的是上图中红色矩形圈出的内容:从上到下分别使用…...
企业微信 企业内部开发 学习笔记
官方文档 文档 术语介绍 引入pom <dependency><groupId>com.github.binarywang</groupId><artifactId>wx-java-cp-spring-boot-starter</artifactId><version>4.5.3.B</version></dependency>核心代码 推送消息 final WxCp…...

03 QT基本控件和功能类
一 进度条 、水平滑动条 垂直滑动条 当在QT中,在已知类名的情况下,要了解类的构造函数 常用属性 及 信号和槽 常用api 特征:可以获取当前控件的值和设置它的当值 ---- int ui->progressBar->setValue(value); //给进度条设置一个整型值 ui->progressBar->value…...
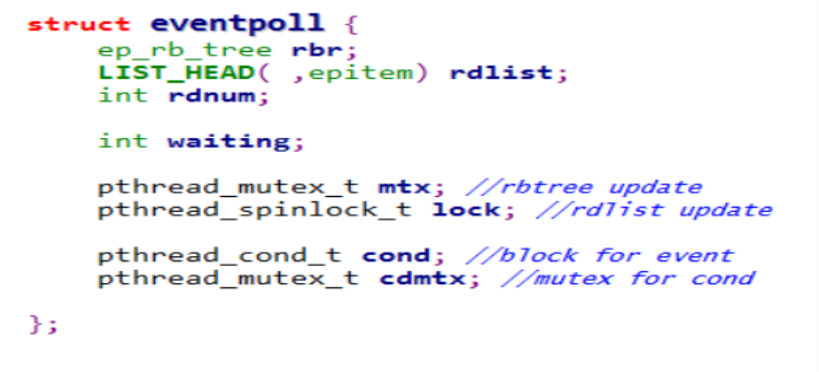
epoll数据结构
目录 1.大量的fd 集合。选择什么数据结构?2、Epoll 数据结构Epitem 的定义Eventpoll 的定义 1.大量的fd 集合。选择什么数据结构? 查找频率很高的数据结构 1.红黑树 2.哈希(扩容缩容) 3. b/btree (降低树的高度&#…...

LINUX学习笔记_GIT操作命令
LINUX学习笔记 GIT操作命令 基本命令 git init:初始化仓库git status:查看文件状态git add:添加文件到暂存区(index)git commit -m “注释”:提交文件到仓库(repository)git log&a…...

第一百二十九天学习记录:数据结构与算法基础:栈和队列(中)(王卓教学视频)
栈的表示和实现 顺序栈的初始化 ##入栈 链栈的表示...
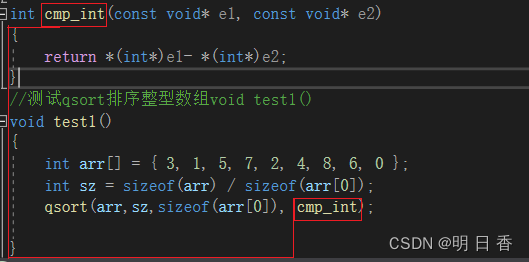
C语言 — qsort 函数
介绍:qsort是一个库函数,用来对数据进行排序,可以排序任意类型的数据。 void qsort (void*base, size_t num, size_t size, int(*compart)(const void*,constvoid*) ) qsort 具有四个参数: …...

开放式耳机哪个好一点?推荐几款优秀的开放式耳机
在追求更广阔的音场和更真实的音质时,开放式耳机是绝对值得考虑的选择。它们以其通透感和自然的音质而备受推崇,带来更逼真的音乐体验。下面我来推荐几款优秀的开放式耳机,满足你对音质和舒适度的要求,可尽情享受音乐的魅力。 一…...
vue-cli前端工程化——创建vue-cli工程 router版本的创建 目录结构 案例初步
目录 引出创建vue-cli前端工程vue-cli是什么自动构建创建vue-cli项目选择Vue的版本号 手动安装进行选择创建成功 手动创建router版多了一个router 运行测试bug解决 Vue项目结构main.jspackage.jsonvue.config.js Vue项目初步hello案例 总结 引出 1.vue-cli是啥,创建…...

Go和Java实现外观模式
Go和Java实现外观模式 下面我们通过一个构造各种形状的案例来说明外观模式的使用。 1、外观模式 外观模式隐藏系统的复杂性,并向客户端提供了一个客户端可以访问系统的接口。这种类型的设计模式属于结构型 模式,它向现有的系统添加一个接口ÿ…...

人工智能(一)基本概念
人工智能之基本概念 常见问题什么是人工智能?人工智能应用在那些地方?人工智能的三种形态图灵测试是啥?人工智能、机器学习和深度学习之间是什么关系?为什么人工智能计算会用到GPU? 机器学习什么是机器学习?…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
