Rust 重载运算符|复数结构的“加减乘除”四则运算

复数
基本概念
复数定义
由实数部分和虚数部分所组成的数,形如a+bi 。
其中a、b为实数,i 为“虚数单位”,i² = -1,即虚数单位的平方等于-1。
a、b分别叫做复数a+bi的实部和虚部。
当b=0时,a+bi=a 为实数;
当b≠0时,a+bi 又称虚数;
当b≠0、a=0时,bi 称为纯虚数。
实数和虚数都是复数的子集。如同实数可以在数轴上表示一样复数也可以在平面上表示,复数x+yi以坐标点(x,y)来表示。表示复数的平面称为“复平面”。
复数相等
两个复数不能比较大小,但当个两个复数的实部和虚部分别相等时,即表示两个复数相等。
共轭复数
如果两个复数的实部相等,虚部互为相反数,那么这两个复数互为共轭复数。
复数的模
复数的实部与虚部的平方和的正的平方根的值称为该复数的模,数学上用与绝对值“|z|”相同的符号来表示。虽然从定义上是不相同的,但两者的物理意思都表示“到原点的距离”。
复数的四则运算
加法(减法)法则
复数的加法法则:设z1=a+bi,z2 =c+di是任意两个复数。两者和的实部是原来两个复数实部的和,它的虚部是原来两个虚部的和。两个复数的和依然是复数。
即(a+bi)±(c+di)=(a±c)+(b±d)
乘法法则
复数的乘法法则:把两个复数相乘,类似两个多项式相乘,结果中i²=-1,把实部与虚部分别合并。两个复数的积仍然是一个复数。
即(a+bi)(c+di)=(ac-bd)+(bc+ad)i
除法法则
复数除法法则:满足(c+di)(x+yi)=(a+bi)的复数x+yi(x,y∈R)叫复数a+bi除以复数c+di的商。
运算方法:可以把除法换算成乘法做,将分子分母同时乘上分母的共轭复数,再用乘法运算。
即(a+bi)/(c+di)=(a+bi)(c-di)/(c*c+d*d)=[(ac+bd)+(bc-ad)i]/(c*c+d*d)
复数的Rust代码实现
结构定义
Rust语言中,没有像python一样内置complex复数数据类型,我们可以用两个浮点数分别表示复数的实部和虚部,自定义一个结构数据类型,表示如下:
struct Complex {
real: f64,
imag: f64,
}
示例代码:
#[derive(Debug)]
struct Complex {real: f64,imag: f64,
}impl Complex { fn new(real: f64, imag: f64) -> Self {Complex { real, imag } }
}fn main() { let z = Complex::new(3.0, 4.0);println!("{:?}", z);println!("{} + {}i", z.real, z.imag);
}注意:#[derive(Debug)] 自动定义了复数结构的输出格式,如以上代码输出如下:
Complex { real: 3.0, imag: 4.0 }
3 + 4i
重载四则运算
复数数据结构不能直接用加减乘除来做复数运算,需要导入标准库ops的运算符:
use std::ops::{Add, Sub, Mul, Div, Neg};
Add, Sub, Mul, Div, Neg 分别表示加减乘除以及相反数,类似C++或者python语言中“重载运算符”的概念。
根据复数的运算法则,写出对应代码:
fn add(self, other: Complex) -> Complex {
Complex {
real: self.real + other.real,
imag: self.imag + other.imag,
}
}fn sub(self, other: Complex) -> Complex {
Complex {
real: self.real - other.real,
imag: self.imag - other.imag,
}
}fn mul(self, other: Complex) -> Complex {
let real = self.real * other.real - self.imag * other.imag;
let imag = self.real * other.imag + self.imag * other.real;
Complex { real, imag }
}fn div(self, other: Complex) -> Complex {
let real = (self.real * other.real + self.imag * other.imag) / (other.real * other.real + other.imag * other.imag);
let imag = (self.imag * other.real - self.real * other.imag) / (other.real * other.real + other.imag * other.imag);
Complex { real, imag }
}fn neg(self) -> Complex {
Complex {
real: -self.real,
imag: -self.imag,
}
}
Rust 重载运算的格式,请见如下示例代码:
use std::ops::{Add, Sub, Mul, Div, Neg};#[derive(Clone, Debug, PartialEq)]
struct Complex {real: f64,imag: f64,
}impl Complex { fn new(real: f64, imag: f64) -> Self {Complex { real, imag } }fn conj(&self) -> Self {Complex { real: self.real, imag: -self.imag }}fn abs(&self) -> f64 {(self.real * self.real + self.imag * self.imag).sqrt()}
}fn abs(z: Complex) -> f64 {(z.real * z.real + z.imag * z.imag).sqrt()
}impl Add<Complex> for Complex {type Output = Complex;fn add(self, other: Complex) -> Complex {Complex {real: self.real + other.real,imag: self.imag + other.imag,} }
} impl Sub<Complex> for Complex {type Output = Complex;fn sub(self, other: Complex) -> Complex {Complex { real: self.real - other.real,imag: self.imag - other.imag,} }
} impl Mul<Complex> for Complex {type Output = Complex; fn mul(self, other: Complex) -> Complex { let real = self.real * other.real - self.imag * other.imag;let imag = self.real * other.imag + self.imag * other.real;Complex { real, imag } }
}impl Div<Complex> for Complex {type Output = Complex;fn div(self, other: Complex) -> Complex {let real = (self.real * other.real + self.imag * other.imag) / (other.real * other.real + other.imag * other.imag);let imag = (self.imag * other.real - self.real * other.imag) / (other.real * other.real + other.imag * other.imag);Complex { real, imag }}
} impl Neg for Complex {type Output = Complex;fn neg(self) -> Complex {Complex {real: -self.real,imag: -self.imag,}}
}fn main() { let z1 = Complex::new(2.0, 3.0);let z2 = Complex::new(3.0, 4.0);let z3 = Complex::new(3.0, -4.0);// 复数的四则运算let complex_add = z1.clone() + z2.clone();println!("{:?} + {:?} = {:?}", z1, z2, complex_add);let complex_sub = z1.clone() - z2.clone();println!("{:?} - {:?} = {:?}", z1, z2, complex_sub);let complex_mul = z1.clone() * z2.clone();println!("{:?} * {:?} = {:?}", z1, z2, complex_mul);let complex_div = z2.clone() / z3.clone();println!("{:?} / {:?} = {:?}", z1, z2, complex_div);// 对比两个复数是否相等println!("{:?}", z1 == z2);// 共轭复数println!("{:?}", z2 == z3.conj());// 复数的相反数println!("{:?}", z2 == -z3.clone() + Complex::new(6.0,0.0));// 复数的模println!("{}", z1.abs());println!("{}", z2.abs());println!("{}", abs(z3));
}
输出:
Complex { real: 2.0, imag: 3.0 } + Complex { real: 3.0, imag: 4.0 } = Complex { real: 5.0, imag: 7.0 }
Complex { real: 2.0, imag: 3.0 } - Complex { real: 3.0, imag: 4.0 } = Complex { real: -1.0, imag: -1.0 }
Complex { real: 2.0, imag: 3.0 } * Complex { real: 3.0, imag: 4.0 } = Complex { real: -6.0, imag: 17.0 }
Complex { real: 2.0, imag: 3.0 } / Complex { real: 3.0, imag: 4.0 } = Complex { real: -0.28, imag: 0.96 }
false
true
true
3.605551275463989
5
5
示例代码中,同时还定义了复数的模 abs(),共轭复数 conj()。
两个复数的相等比较 z1 == z2,需要 #[derive(PartialEq)] 支持。
自定义 trait Display
复数结构的原始 Debug trait 表达的输出格式比较繁复,如:
Complex { real: 2.0, imag: 3.0 } + Complex { real: 3.0, imag: 4.0 } = Complex { real: 5.0, imag: 7.0 }
想要输出和数学中相同的表达(如 a + bi),需要自定义一个 Display trait,代码如下:
impl std::fmt::Display for Complex {
fn fmt(&self, formatter: &mut std::fmt::Formatter) -> std::fmt::Result {
if self.imag == 0.0 {
formatter.write_str(&format!("{}", self.real))
} else {
let (abs, sign) = if self.imag > 0.0 {
(self.imag, "+" )
} else {
(-self.imag, "-" )
};
if abs == 1.0 {
formatter.write_str(&format!("({} {} i)", self.real, sign))
} else {
formatter.write_str(&format!("({} {} {}i)", self.real, sign, abs))
}
}
}
}
输出格式分三种情况:虚部为0,正数和负数。另外当虚部绝对值为1时省略1仅输出i虚数单位。
完整代码如下:
use std::ops::{Add, Sub, Mul, Div, Neg};#[derive(Clone, PartialEq)]
struct Complex {real: f64,imag: f64,
}impl std::fmt::Display for Complex {fn fmt(&self, formatter: &mut std::fmt::Formatter) -> std::fmt::Result {if self.imag == 0.0 {formatter.write_str(&format!("{}", self.real))} else {let (abs, sign) = if self.imag > 0.0 { (self.imag, "+" )} else {(-self.imag, "-" )};if abs == 1.0 {formatter.write_str(&format!("({} {} i)", self.real, sign))} else {formatter.write_str(&format!("({} {} {}i)", self.real, sign, abs))}}}
}impl Complex { fn new(real: f64, imag: f64) -> Self {Complex { real, imag } }fn conj(&self) -> Self {Complex { real: self.real, imag: -self.imag }}fn abs(&self) -> f64 {(self.real * self.real + self.imag * self.imag).sqrt()}
}fn abs(z: Complex) -> f64 {(z.real * z.real + z.imag * z.imag).sqrt()
}impl Add<Complex> for Complex {type Output = Complex;fn add(self, other: Complex) -> Complex {Complex {real: self.real + other.real,imag: self.imag + other.imag,} }
} impl Sub<Complex> for Complex {type Output = Complex;fn sub(self, other: Complex) -> Complex {Complex { real: self.real - other.real,imag: self.imag - other.imag,} }
} impl Mul<Complex> for Complex {type Output = Complex; fn mul(self, other: Complex) -> Complex { let real = self.real * other.real - self.imag * other.imag;let imag = self.real * other.imag + self.imag * other.real;Complex { real, imag } }
}impl Div<Complex> for Complex {type Output = Complex;fn div(self, other: Complex) -> Complex {let real = (self.real * other.real + self.imag * other.imag) / (other.real * other.real + other.imag * other.imag);let imag = (self.imag * other.real - self.real * other.imag) / (other.real * other.real + other.imag * other.imag);Complex { real, imag }}
} impl Neg for Complex {type Output = Complex;fn neg(self) -> Complex {Complex {real: -self.real,imag: -self.imag,}}
}fn main() {let z1 = Complex::new(2.0, 3.0);let z2 = Complex::new(3.0, 4.0);let z3 = Complex::new(3.0, -4.0);// 复数的四则运算let complex_add = z1.clone() + z2.clone();println!("{} + {} = {}", z1, z2, complex_add);let z = Complex::new(1.5, 0.5);println!("{} + {} = {}", z, z, z.clone() + z.clone());let complex_sub = z1.clone() - z2.clone();println!("{} - {} = {}", z1, z2, complex_sub);let complex_sub = z1.clone() - z1.clone();println!("{} - {} = {}", z1, z1, complex_sub);let complex_mul = z1.clone() * z2.clone();println!("{} * {} = {}", z1, z2, complex_mul);let complex_mul = z2.clone() * z3.clone();println!("{} * {} = {}", z2, z3, complex_mul);let complex_div = z2.clone() / z3.clone();println!("{} / {} = {}", z1, z2, complex_div);let complex_div = Complex::new(1.0,0.0) / z2.clone();println!("1 / {} = {}", z2, complex_div);// 对比两个复数是否相等println!("{:?}", z1 == z2);// 共轭复数println!("{:?}", z2 == z3.conj());// 复数的相反数println!("{:?}", z2 == -z3.clone() + Complex::new(6.0,0.0));// 复数的模println!("{}", z1.abs());println!("{}", z2.abs());println!("{}", abs(z3));
}输出:
(2 + 3i) + (3 + 4i) = (5 + 7i)
(1.5 + 0.5i) + (1.5 + 0.5i) = (3 + i)
(2 + 3i) - (3 + 4i) = (-1 - i)
(2 + 3i) - (2 + 3i) = 0
(2 + 3i) * (3 + 4i) = (-6 + 17i)
(3 + 4i) * (3 - 4i) = 25
(2 + 3i) / (3 + 4i) = (-0.28 + 0.96i)
1 / (3 + 4i) = (0.12 - 0.16i)
false
true
true
3.605551275463989
5
5
小结
如此,复数的四则运算基本都实现了,当然复数还有三角表示式和指数表示式,根据它们的数学定义写出相当代码应该不是很难。有了复数三角式,就能方便地定义出复数的开方运算,有空可以写写这方面的代码。
本文完
相关文章:

Rust 重载运算符|复数结构的“加减乘除”四则运算
复数 基本概念 复数定义 由实数部分和虚数部分所组成的数,形如a+bi 。 其中a、b为实数,i 为“虚数单位”,i -1,即虚数单位的平方等于-1。 a、b分别叫做复数a+bi的实部和虚部。 当b0时,a&…...

Oracle删除表空间
1.检查表空间状态 SELECT tablespace_name, status FROM dba_tablespaces;备注:tablespace_name表示删除表空间的名称,status为表空间的状态。如果状态为ONLINE,表示表空间当前正在使用,不能被删除。 2.关闭表空间 ALTER TABLE…...

Mysql - 配置Mysql主从复制-keepalived高可用-读写分离集群
目录 高可用: 为什么需要高可用呢? 高可用的主要作用: keepalived是什么?它用在哪里? 什么是VRRP协议,它的作用是什么? 搭建一个基于keepalived的高可用Mysql主从复制读写分离集群 一、项…...

Qt QLineEdit输入时限制,采用正则表达式
QLineEdit 正则 序言使用方法正则表达式使用例子 序言 老是有人在群里问这个,所以我干脆写一篇方便予人查看,很简单的小功能。 使用方法 Qt5 #include <QRegExpValidator> //#include "qvalidator.h"ui->lineEdit->setValida…...

【CSS】文本效果
文本溢出、整字换行、换行规则以及书写模式 代码: <style> p.test1 {white-space: nowrap; width: 200px; border: 1px solid #000000;overflow: hidden;text-overflow: clip; }p.test2 {white-space: nowrap; width: 200px; border: 1px solid #000000;ove…...
Django快速上手,写一个简单的页面,快来看看吧~
还没有安装Django,以及不会创建Django项目的小伙伴,可以先看看博主这篇文章:http://t.csdn.cn/Ly7yM 目录 1、项目创建完成后,需要注意的点: 2、创建app 3、app的各个目录的作用 4、快速上手 4.1、注册app 4.2、U…...

【Express.js】数据库初始化
数据库初始化 在软件开发阶段和测试阶段,为了方便调试,我们通常会进行一系列的数据库初始化操作,比如重置数据表,插入记录等等,或者在部署阶段进行数据初始化的操作 根据前面章节介绍过的 knex.js 和 sequelize.js&…...

【数理知识】三维空间旋转矩阵的欧拉角表示法,四元数表示法,两者之间的转换,Matlab 代码实现
序号内容1【数理知识】自由度 degree of freedom 及自由度的计算方法2【数理知识】刚体 rigid body 及刚体的运动3【数理知识】刚体基本运动,平动,转动4【数理知识】向量数乘,内积,外积,matlab代码实现5【数理知识】最…...

【业务功能篇63】Springboot聊聊 过滤器和拦截器
过滤器的场景:过滤器通常用于对数据或资源进行筛选、修改或转换的场景。例如,在一个电子商务网站中,用户进行商品搜索时,你可以使用过滤器来过滤特定的商品类别、价格范围或其他条件,以便用户仅看到符合筛选条件的结果…...
提高学生学习效率的模拟考试系统
在如今竞争激烈的社会环境下,提高学生的学习效率显得尤为重要。为了帮助学生评估自己的学习水平并提供有针对性的学习建议,开发一款模拟考试系统是非常必要的。 一、学生信息录入 模拟考试系统首先需要学生信息录入功能。学生可以通过一个简单的表单填…...

解决QWebEngineView在linux下加载本地html失败的问题
通常我们使用QWebEngineView加载本地html文件时,是通过 void load(const QUrl &url) void setUrl(const QUrl &url) 两个函数,传入html的相对或绝对路径,进行加载。 而在linux(uos x86)下运行时,却发现加载失败…...

如何使用Redis实现内容推送功能
导读 在日常使用中,我们经常能看见内容推送功能。 常见的场景有,比如你在bilibili关注了某个up主,当up主发布视频后,就会推送到你的收件箱或者是动态中,让粉丝能够及时得知所关注的人发布了内容。 又比如朋友圈&…...
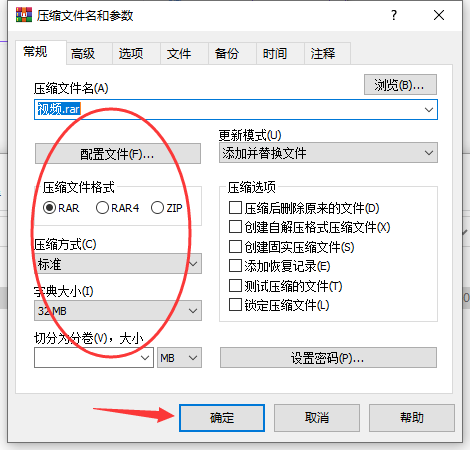
怎么对视频进行压缩?
怎么对视频进行压缩?视频压缩,我们都知道是将视频文件进行压缩变小的过程,是我们日常办公中较为常用的手段。现如今,在视频技术不断发展与创新的基础上,视频分辨率也在不断提高,进而导致文件占有量也非常大…...

redisson配置类---SpringBoot集成、redis单机和集群模式配置
1项目配置文件: 1.1:pom.xml <dependency><groupId>org.redisson</groupId><artifactId>redisson-spring-boot-starter</artifactId><version>3.17.7</version></dependency> 1.2 application.yml配置…...
瓴羊发布All in One 产品,零售SaaS的尽头是DaaS?
“打破烟囱、化繁为简,让丰富的能力、数据和智能All in One”,这是瓴羊新发布的产品瓴羊One承担的使命,也意味着瓴羊DaaS事业迈入了一个新阶段。 成立伊始,瓴羊就打出了“Not SaaS,But DaaS”旗号,将自己的…...
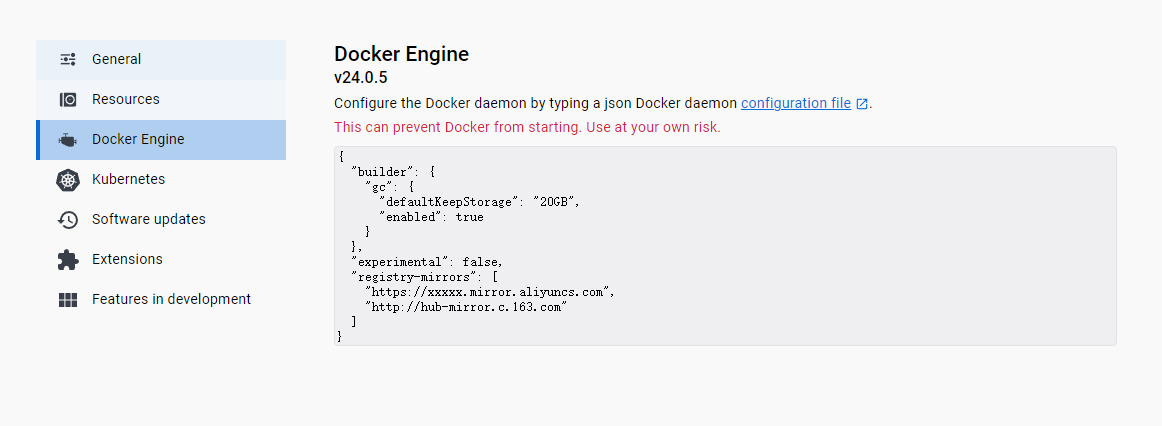
win10中Docker安装、构建镜像、创建容器、Vscode连接实例
Docker方便一键构建项目所需的运行环境:首先构建镜像(Image)。然后镜像实例化成为容器(Container),构成项目的运行环境。最后Vscode连接容器,方便我们在本地进行开发。下面以一个简单的例子介绍在win10中实现:Docker安装、构建镜像…...

贝锐蒲公英:快速搭建连锁门店监控体系,赋能企业高效管理
随着国民生活水平的提高和零售场景的变革,消费者对于餐饮类目的消费支出不断增加,线下社区生鲜商超作为下沉市场最主要的消费场景之一,蕴藏着巨大价值机会。 对于线下连锁生鲜超市而言,连锁门店多、员工多,门店管理时会…...

c++ WinInet InternetOpenUrl下载中文文件
windows自带的WinInet,几个函数就可以实现http文件下载, 且可获取文件大小,进度条等。 在用WinInet下载文件时,遇到个问题, 如果是中文,下载下来的文件大小为0 英文文件正常,为什么呢? bool WWWFileBuffer(const char* host, const char* path, char* outBuffer, in…...
算法通过村第三关-数组青铜笔记|单调数组
文章目录 前言单调数组问题搜索插入位置:数组合并问题:总结 前言 提示:本份真诚面对自己、坦然无碍面对他人,就是优雅。 数组中的比较经典性问题: 单调数组问题数组合并问题 单调数组问题 参考例子:896. 单调数列…...
Springboot MultipartFile文件上传与下载
yml文件配置是否可以上传及上传附件大小 servlet:multipart:# 允许文件上传enabled: true# 单个文件大小max-file-size: 20MB# 设置总上传的文件大小max-request-size: 50MB /*** param files* param request* Description 上传文件* Throws* Return java.util.List* Date 202…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
