简单记录牛客top101算法题(初级题C语言实现)BM24 二叉树的中序遍历 BM28 二叉树的最大深度 BM29 二叉树中和为某一值的路径
1. BM24 二叉树的中序/后续遍历
要求:给定一个二叉树的根节点root,返回它的中序遍历结果。
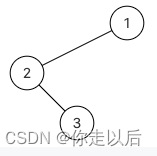
输入:{1,2,#,#,3}
返回值:[2,3,1]
1.1 自己的整体思路(与二叉树的前序遍历大致一样)
- 使用二叉树的前序遍历方法,递归完成二叉树元素的访问。
- 先遍历二叉树,求出二叉树的结点数量以后,再申请数组,这样节省内存大小。
- 二叉树的前中后序遍历,只需要改变访问根结点的代码位置,其与递归左子树和右子树的位置,代表是前中后序的一种。
#include <malloc.h>
#include <stdbool.h>
#include <stdint.h>
#include <stdio.h>
#include <string.h>
int TreeSize(struct TreeNode* root) { //判断二叉树有多少个结点if (root == NULL) {return 0;}return TreeSize(root->left) + TreeSize(root->right) + 1;
}
void visit_root(struct TreeNode* root, int* arr,int *a){ //访问根结点*(arr + *a) = root->val; //存下根结点元素(*a)++; //索引++
}void Preorder(struct TreeNode* root, int* arr,int *a){ //遍历二叉树if (root!=NULL) {Preorder(root->left,arr,a); //递归左结点visit_root(root,arr,a); //访问根结点 //如果把这一行放到下面一行,就是后序遍历,其他的代码不用变的Preorder(root->right,arr,a); //递归右结点}}
int* inorderTraversal(struct TreeNode* root, int* returnSize ) { //中序遍历// int n; //这里没有初始化,导致程序卡死了int n = 0;int *i = &n;int count = TreeSize(root); //计算二叉树有多少结点printf("val = %d\r\n",count);int *array = (int *)malloc(count * sizeof(int)); //申请一个空数组Preorder(root, array, i); //遍历二叉树*returnSize = *i;return array;
}
1.2 小结
1.2.1 求二叉树结点的个数
int TreeSize(struct TreeNode* root) { //判断二叉树有多少个结点if (root == NULL) {return 0;}return TreeSize(root->left) + TreeSize(root->right) + 1;
}
假设这个二叉树如下所示:
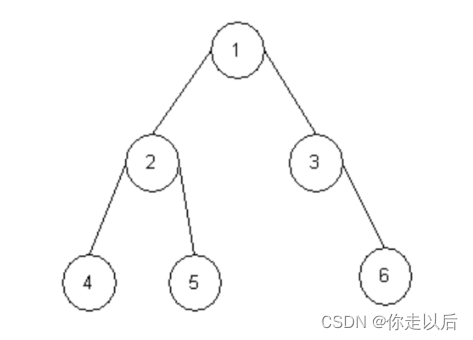
第一次进到这个程序中:结点1不为NULL,返回的是TreeSize(结点2) + TreeSize(结点3) + 1;
运行TreeSize(结点2) :结点2不为NULL,返回的是TreeSize(结点4) + TreeSize(结点5) + 1;
运行TreeSize(结点4) :结点4不为NULL,返回的是TreeSize(NULL) + TreeSize(NULL) + 1,也就是返回的0 + 0 +1 =1;
返回上面一层TreeSize(结点5):结点5不为NULL,返回的是TreeSize(NULL) + TreeSize(NULL) + 1,也就是返回的0 + 0 +1 =1;目前TreeSize(结点2) 返回的值就是1+1+1 = 3;
运行TreeSize(结点3):结点3不为NULL,返回的是TreeSize(NULL) + TreeSize(结点6) + 1;
运行TreeSize(结点6):结点6不为NULL,返回的是TreeSize(NULL) + TreeSize(NULL) + 1,也就是返回的0 + 0 +1 =1;目前TreeSize(结点3) 返回的值就是0+1+1 = 2;
所以整体TreeSize(结点2) + TreeSize(结点3) + 1 = 3 + 2 + 1 = 6,也就计算出来了二叉树结点的个数。
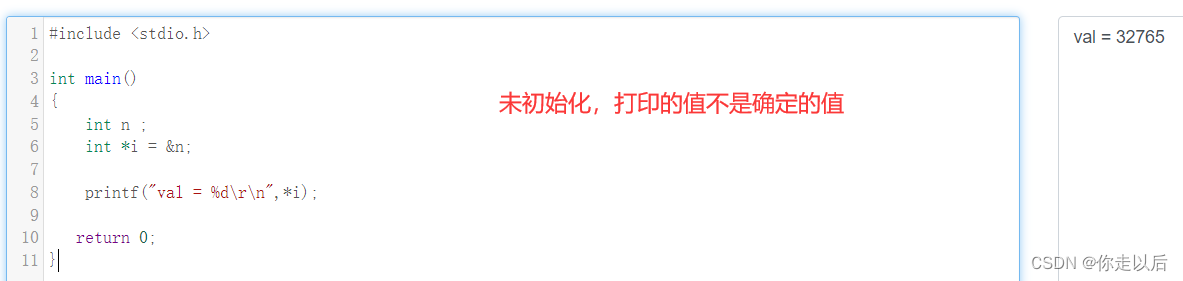
1.2.2 使用指针时,未初始化变量初值
使用指针时,未初始化变量初值,导致程序报错。
int n;
int *i = &n;
2. BM28 二叉树的最大深度
要求:求给定二叉树的最大深度,深度是指树的根节点到任一叶子节点路径上节点的数量。最大深度是所有叶子节点的深度的最大值.
这个题,没有什么思路,看视频讲解的方法,代码如下:
#include <stdio.h>
int maxDepth(struct TreeNode* root ){int n1 = 0;int n2 = 0;if (root == NULL) {return 0;}n1 = maxDepth(root->left);n2 = maxDepth(root->right);return n1 > n2 ? n1 + 1 : n2 + 1;
}
假设这个二叉树如下所示,还是以下面这个二叉树为例,看这个代码具体运行的步骤:
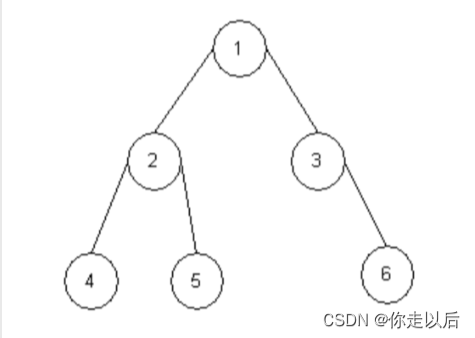
第一次进到这个程序中:结点1(根结点)不为NULL,运行 n1 = maxDepth(根结点的左结点(结点2));
因为结点2不为NULL,此时传入结点2进入函数:运行n1 = maxDepth(结点2的左结点(结点4));
因为结点4不为NULL,此时传入结点4进入函数:运行n1 = maxDepth(结点4的左结点(NULL)),并返回了n1 =0。
因为结点4的左结点为NULL,程序会执行下面一句,n2 = maxDepth(结点4的右结点(NULL)),并返回了n2 =0。
所以对于结点4,n1 = n2=0,程序会返回1。这里也就是结点2的左结点,n1 = maxDepth(结点2的左结点(结点4)),这里的n1 = 1;
此时程序会返回到,结点2上面,运行n2 = maxDepth(结点2的右结点(结点5));
因为结点5不为NULL,此时传入结点5进入函数:运行n1 = maxDepth(结点5的左结点(NULL)),并返回了n1 =0。
因为结点5的左结点为NULL,程序会执行下面一句,n2 = maxDepth(结点5的右结点(NULL)),并返回了n2 =0。
所以对于结点5,n1 = n2=0,程序会返回1。这里也就是结点2的右结点,n2= maxDepth(结点2的右结点(结点5)),这里的n2 = 1;
此时对于结点2来说,n1=1,n2=1,所以会返回2。这里也就是结点1的左结点,n1 = maxDepth(结点1的左结点(结点2)),这里的n1 = 2;
此时程序会返回到,结点1上面,运行n2 = maxDepth(结点1的右结点(结点3));
因为结点3不为NULL,此时传入结点3进入函数:运行n1 = maxDepth(结点3的左结点(NULL)),并返回了n1 =0。
因为结点3的左结点为NULL,程序会执行下面一句,n2 = maxDepth(结点3的右结点(结点6))。
因为结点6不为NULL,此时传入结点6进入函数:运行n1 = maxDepth(结点6的左结点(NULL)),并返回了n1 =0。
因为结点6的左结点为NULL,程序会执行下面一句,n2 = maxDepth(结点6的右结点(NULL)),并返回了n2 =0。
所以对于结点6,n1 = n2 = 0,程序会返回1。这里也就是结点3的右结点,n2 = maxDepth(结点3的右结点(结点6)),这里的 n2 = 1;
此时对于结点3来说,n1 = 0,n2 = 1,所以会返回2。也就是结点1中的n2 = maxDepth(结点1的右结点(结点3)) = 2;
此时对于结点1来说,n1 = 2,n2 = 2,所以会返回3。程序结束,二叉树的最大深度是3。
3. BM29 二叉树中和为某一值的路径
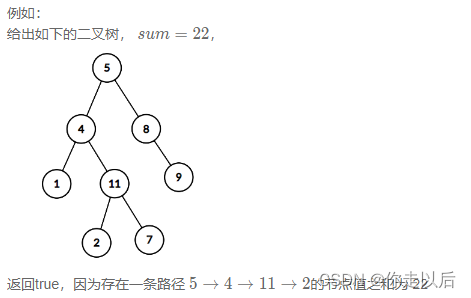
要求:给定一个二叉树root和一个值 sum ,判断是否有从根节点到叶子节点的节点值之和等于 sum 的路径。
1.该题路径定义为从树的根结点开始往下一直到叶子结点所经过的结点
2.叶子节点是指没有子节点的节点
3.路径只能从父节点到子节点,不能从子节点到父节点
4.总节点数目为n
这个题,也没有什么思路,看视频讲解的方法,代码如下:
bool bianli(struct TreeNode* root, int sum, int sum1){ //遍历一个子树,必须要返回一个值if (root == NULL) {return false;}sum1 += root->val; //求和if (root->left == NULL && root->right == NULL) {if (sum1 == sum){return true;}else{return false;}}bool leftHasPath = bianli(root->left, sum, sum1);bool rightHasPath = bianli(root->right, sum, sum1);return leftHasPath || rightHasPath;
}bool hasPathSum(struct TreeNode* root, int sum){//如何遍历一个子树// int * arr = (int *)malloc(1000*sizeof(int)); int a = 0; //求和return bianli(root,sum,a);
}
假设这个二叉树如下所示,还是以下面这个二叉树为例,看这个代码具体运行的步骤:(结点每一排依次称为结点1,2,3…)
第一次进到这个程序中:结点1(根结点)不为NULL,sum1 = 5; 然后进入这一句:bool leftHasPath = bianli(结点2, 22, 5);
sum1 = 5 + 4 = 9; bool leftHasPath = bianli(结点4, 22, 9); 这是结点3的左结点。
sum1 = 9 + 1 = 10;return false; 返回上一层循环,返回到结点3, bool rightHasPath = bianli(结点5, 22, 9);因为到结点3的时候,sum1的值就是9。
sum1 = 9 + 11 = 20; bool leftHasPath = bianli(结点7, 22, 20);
sum1 = 20 + 2 = 22; return true;综上就是leftHasPath = false; rightHasPath = true;程序会继续运行,直到遍历完所有可能的路径。最终会返回true。
改进代码如下,找到一条路径后就会停止(不会遍历所有的路径的):
bool findPath(struct TreeNode* node, int targetSum, int currentSum) {if (node == NULL) {return false;}currentSum += node->val;if (node->left == NULL && node->right == NULL && currentSum == targetSum) {return true;}bool foundInLeft = findPath(node->left, targetSum, currentSum);if (foundInLeft) {return true; // 找到路径,立即中断递归}bool foundInRight = findPath(node->right, targetSum, currentSum);if (foundInRight) {return true; // 找到路径,立即中断递归}return false; // 未找到路径
}bool hasPathSum(struct TreeNode* root, int sum){//如何遍历一个子树// int * arr = (int *)malloc(1000*sizeof(int)); int a = 0; //求和return findPath(root,sum,a);
}
假设这个二叉树如下所示,还是以下面这个二叉树为例,看这个代码具体运行的步骤:
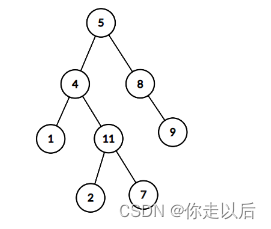
第一次进到这个程序中:结点1(根结点)不为NULL,currentSum = 5; 然后进入这一句:bool foundInLeft = findPath(结点2, 22, 5);
currentSum = 5 + 4 = 9; bool foundInLeft = findPath(结点4, 22, 9);
currentSum = 9 + 1 = 10; bool foundInLeft = findPath(NULL, 22, 10); return false;并返回到了结点2了。
bool foundInRight = findPath(结点5, 22, 9); currentSum = 9 + 11 = 20; bool foundInLeft = findPath(结点7, 22, 20);
currentSum = 20 + 2 = 22; return true; 程序不会会继续运行,不会遍历完所有可能的路径。当找到路径后,递归会立即中断,从而停止遍历。
相关文章:

简单记录牛客top101算法题(初级题C语言实现)BM24 二叉树的中序遍历 BM28 二叉树的最大深度 BM29 二叉树中和为某一值的路径
1. BM24 二叉树的中序/后续遍历 要求:给定一个二叉树的根节点root,返回它的中序遍历结果。 输入:{1,2,#,#,3} 返回值:[2,3,1]1.1 自己的整体思路(与二叉树的前序遍…...
前后端分离------后端创建笔记(05)用户列表查询接口(上)
本文章转载于【SpringBootVue】全网最简单但实用的前后端分离项目实战笔记 - 前端_大菜007的博客-CSDN博客 仅用于学习和讨论,如有侵权请联系 源码:https://gitee.com/green_vegetables/x-admin-project.git 素材:https://pan.baidu.com/s/…...
性能测试|App性能测试需要关注的指标
一、Android客户端性能测试常见指标: 1、内存 2、CPU 3、流量 4、电量 5、启动速度 6、滑动速度、界面切换速度 7、与服务器交互的网络速度 二、预期标准指定原则 1、分析竞争对手的产品,所有指标要强于竞品 2、产品经理给出的预期性能指标数据…...
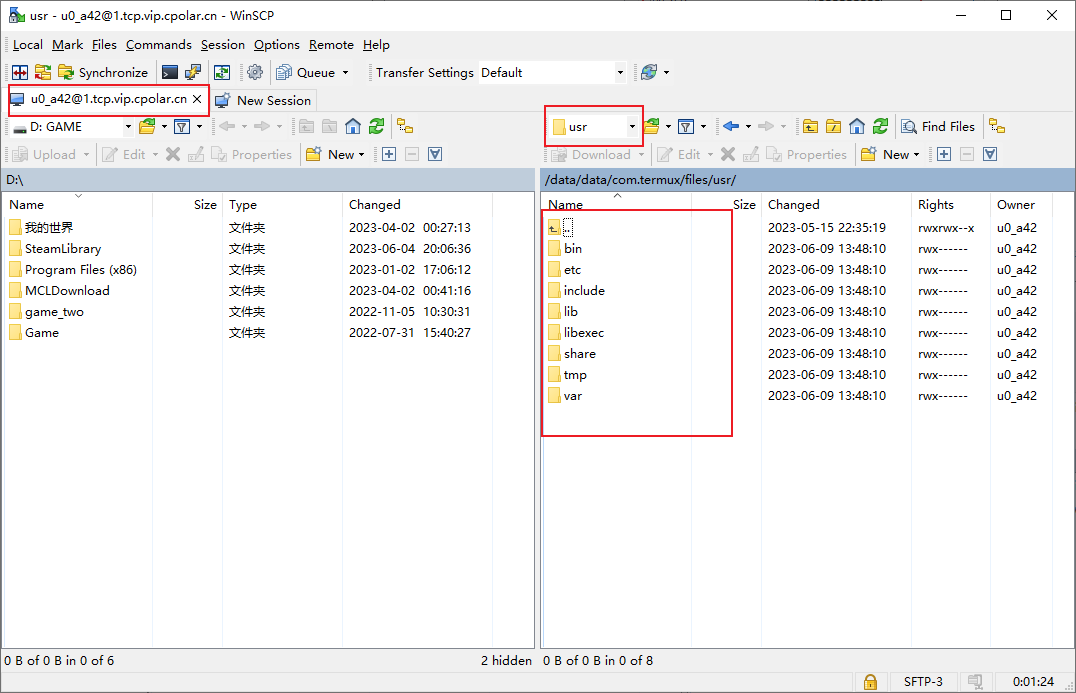
Termux SFTP 进行远程文件传输
文章目录 1. 安装openSSH2. 安装cpolar3. 远程SFTP连接配置4. 远程SFTP访问4. 配置固定远程连接地址 SFTP(SSH File Transfer Protocol)是一种基于SSH(Secure Shell)安全协议的文件传输协议。与FTP协议相比,SFTP使用了…...

Sqlite3简介
SQLite3 简介 SQLite3 是一种轻量级的嵌入式数据库引擎,被广泛应用于各种应用程序中,包括移动设备、桌面应用程序和嵌入式系统。它以其简单、高效和零配置的特点而受到开发者的喜爱。 以下是 SQLite3 的一些重要特点: 嵌入式数据库引擎&…...

K8S调度
K8S调度 一、List-Watch 机制 controller-manager、scheduler、kubelet 通过 List-Watch 机制监听 apiserver 发出的事件,apiserver 通过 List-Watch 机制监听 etcd 发出的事件1.scheduler 的调度策略 预选策略/预算策略:通过调度算法过滤掉不满足条件…...

vue+element多层表单校验prop和rules
核心点:外层循环是item和index,内层循环是item2和index2 如果都是定义的同一个属性名 外层循环得写:prop"block.index.numerical" 同理内层循环就得写:prop"objectSpecs. index2 .numerical" 校验函数方法 :rules"getRules(it…...
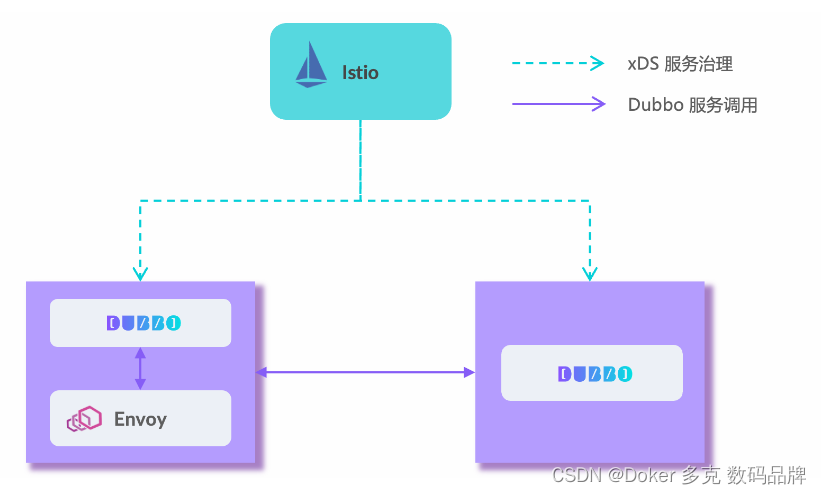
Dubbo 核心概念和架构
以上是 Dubbo 的工作原理图,从抽象架构上分为两层:服务治理抽象控制面 和 Dubbo 数据面 。 服务治理控制面。服务治理控制面不是特指如注册中心类的单个具体组件,而是对 Dubbo 治理体系的抽象表达。控制面包含协调服务发现的注册中心、流量管…...
【数据结构OJ题】反转链表
原题链接:https://leetcode.cn/problems/reverse-linked-list/description/ 目录 1. 题目描述 2. 思路分析 3. 代码实现 1. 题目描述 2. 思路分析 方法一:三指针翻转法 使用三个结构体指针n1,n2,n3,原地修改结点…...

Java8 Stream 之groupingBy 分组讲解
本文主要讲解:Java 8 Stream之Collectors.groupingBy()分组示例 Collectors.groupingBy() 分组之常见用法 功能代码: /** * 使用java8 stream groupingBy操作,按城市分组list */ public void groupingByCity() { Map<String, List<Em…...

优哲SSD大文件写性能测试
SDD磁盘性能测试: 空盘: 大文件读,写,读写(4/6)性能测试,删除性能测试,N进程,N线程 小文件读,写,读写(4/6)性能测试&am…...

Python基础教程: json序列化详细用法介绍
前言 嗨喽,大家好呀~这里是爱看美女的茜茜呐 Python内置的json模块提供了非常完善的对象到JSON格式的转换。 废话不多说,我们先看看如何把Python对象变成一个JSON: d dict(nameKaven, age17, sexMale) print(json.dumps(d)) # {"na…...

一张图看懂 USDT三种类型地址 Omni、ERC20、TRC20的区别
USDT是当前实用最广泛,市值最高的稳定币,它是中心化的公司Tether发行的。在今年的4月17日之前,市场上存在着2种不同类型的USDT。4月17日又多了一种波场TRC20协议发行的USDT,它们各自有什么区别呢?哪个转账最快到账?哪…...
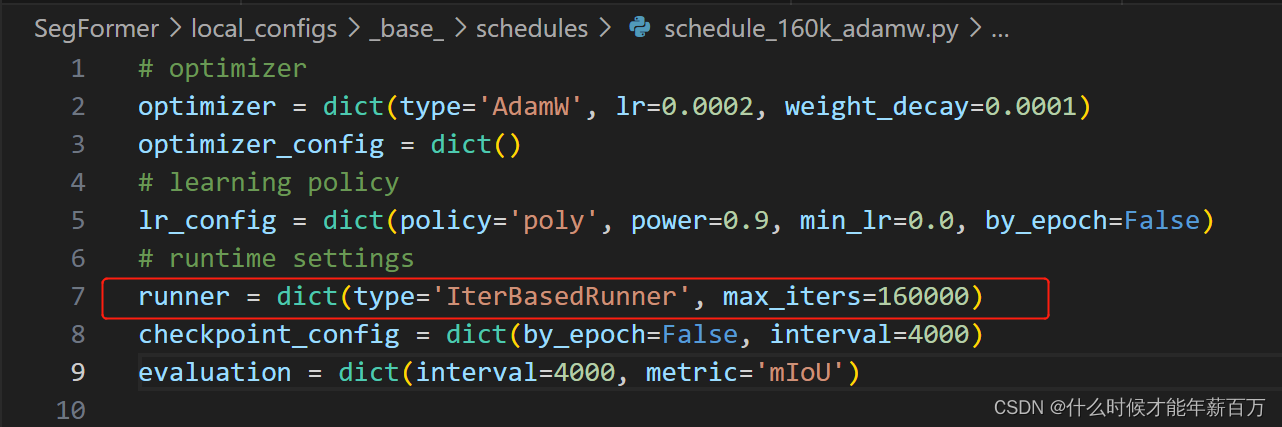
SegFormer之模型训练
单卡训练,所有配置文件里的【SyncBN】改为【BN】 启动训练 (1)终端直接运行 python tools/train.py local_configs/segformer/B1/segformer.b1.512x512.ade.160k.py (2)在编辑器中运行 在 [config] 前面加上’–‘将…...
Azure资源命名和标记决策指南
参考 azure创建虚拟机在虚拟机中选择编辑标签,并添加标记,点击应用 3.到主页中转到所有资源 4. 添加筛选器并应用 5.查看结果,筛选根据给服务器定义的标签筛选出结果。 参考链接: https://learn.microsoft.com/zh-cn/azure/cloud-adoption…...

【在一个升序数组中插入一个数仍升序输出】
在一个升序数组中插入一个数仍升序输出 题目举例: 有一个升序数组nums,给一个数字data,将data插入数组nums中仍旧保证nums升序,返回数组中有效元素个数。 比如:nums[100] {1, 2, 3, 5, 6, 7, 8, 9} size 8 data 4 …...

图像去雨、去雪、去雾论文学习记录
All_in_One_Bad_Weather_Removal_Using_Architectural_Search 这篇论文发表于CVPR2020,提出一种可以应对多种恶劣天气的去噪模型,可以同时进行去雨、去雪、去雾操作。但该部分代码似乎没有开源。 提出的问题: 当下的模型只能针对一种恶劣天气…...
YARN框架和其工作原理流程介绍
目录 一、YARN简介 二、YARN的由来 三、YARN的基本设计思想 四、YARN 的基本架构 4.1 基本架构图 4.2 基本组件介绍 4.2.1 ResourceManager 4.2.1.1 任务调度器(Resource Scheduler) 4.2.1.2 应用程序管理器(Applications Manager) 4.2.1.3 其他…...

多维时序 | MATLAB实现ZOA-CNN-BiGRU-Attention多变量时间序列预测
多维时序 | MATLAB实现ZOA-CNN-BiGRU-Attention多变量时间序列预测 目录 多维时序 | MATLAB实现ZOA-CNN-BiGRU-Attention多变量时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 1.Matlab基于ZOA-CNN-BiGRU-Attention斑马优化卷积双向门控循环单元网络…...

centos上下载redis
1.redis 特点 Redis特性(8个) 1 速度快:10w ops(每秒10w读写),数据存在内存中,c语言实现,单线程模型 2 持久化:rdb和aof 3 多种数据结构: 5大数据结构 …...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
