【数据管理】谈谈哈希原理和散列表
一、说明
提起哈希,有人要说:不就是一个稀疏表格么,谈的上什么原理?我说:非也,哈希是是那种看似无物,其实解决大问题的东西。如何提高数据管理效率?这是个问题,随着这个问题的深度接触,您就会发现,哈希是一个不错选择,而且配合哈希还有不少的操作,似乎不为人知。
二、从数据表的维护说起
2.1 数据库的插入删除
我们知道,数据库最重要的维护不外乎key。数据库水平高低,就看你对key维护有何独到的设计。这里我们把key抽象成电话号码,且看如何维护?
假设我们要设计一个以电话号码(作为键)存储员工记录的系统。我们希望高效地执行以下查询:
- 插入电话号码和相应的信息。
- 搜索电话号码并获取信息。
- 删除电话号码和相关信息。
我们可以想到使用如下数据结构来维护不同电话号码的信息。
- 电话号码和记录的数组。
- 电话号码和记录的链接列表。
- 以电话号码为键的平衡二叉搜索树。
- 直接访问表。
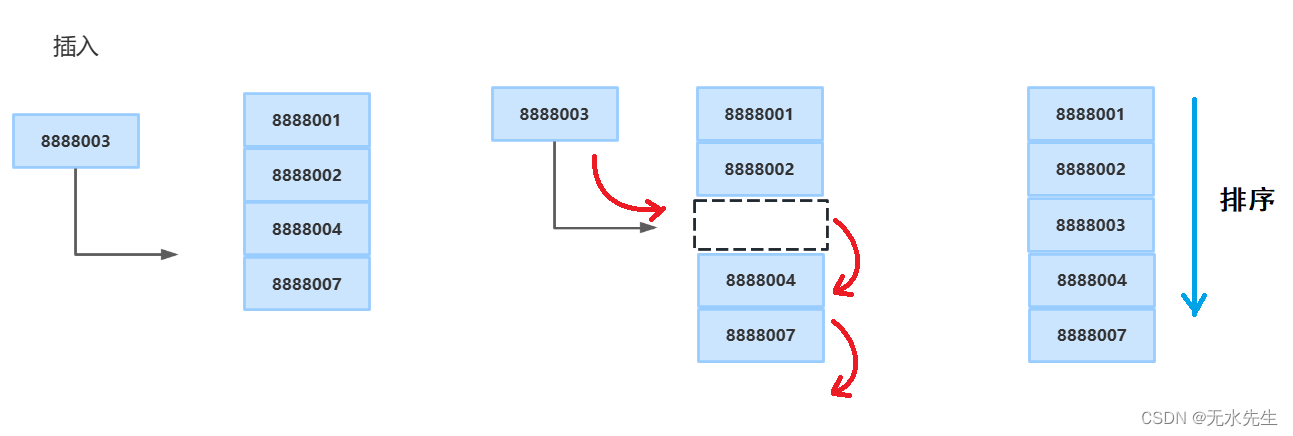
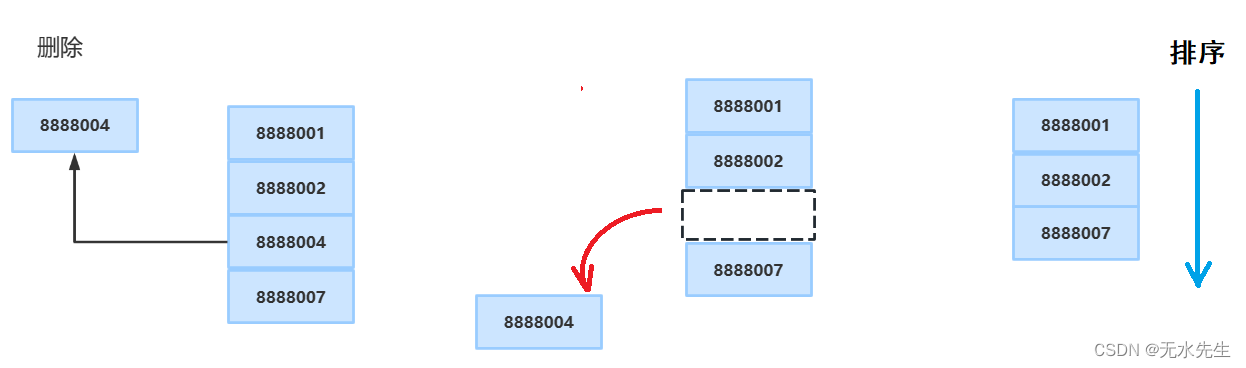
对于数组和链表,我们需要以线性方式搜索,这在实践中可能代价高昂。如果我们使用数组并保持数据排序,那么使用二进制搜索可以在 O(Logn) 时间内搜索电话号码,但是插入和删除操作变得昂贵,因为我们必须维护排序顺序。
使用平衡二叉搜索树,我们得到适度的搜索、插入和删除时间。
以上的数据维护是过去的老式想法,因为存储是昂贵的。所以,索引数据(电话号)需要密集排列,中间没有间隙。因此插入、删除、排序成了必须的维护手段。
2.2 全预留表格
所谓哈希表的稀疏性,还不如叫做全预留表格。也就是不管你的电话号出不出现,我总是预留一个超大表格,该表格足以覆盖电话号码的全部。比如,对于电话号码,我们首先做一个00000000-99999999的大数组,该数组足以满足任意电话号码的存取,而且常驻内存。以上电话号码的哈希表如图。
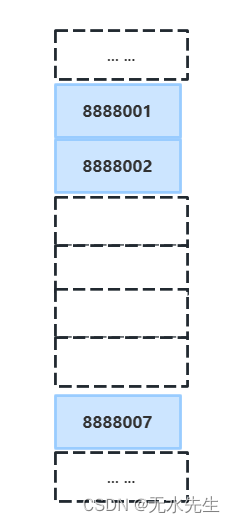
这种设计看似蠢笨,然而,在现实中的内存数据库全是这种模式:用大内存换取时间。因而使得dds协议,rtps协议得以实现,比如redis数据库就是这种模式。
如果电话号码不存在,则数组中的条目为 NIL,否则数组条目存储指向records corresponding to phone number. 时间复杂度方面这个解决方案是最好的,我们可以在 O(1) 时间内完成所有操作。例如插入一个电话号码,我们创建一个包含给定电话号码详细信息的记录,使用 phone number 作为索引,并将指向创建的记录的指针存储在表中。
这个解决方案有很多实际限制。这个解决方案的第一个问题是需要额外的空间是巨大的。例如,如果电话号码是 n 位数字,我们需要 O(m * 10n) 表空间,其中 m 是要记录的指针的大小。问题是编程语言中的整数可能不会存储 n 位数字。
由于上述限制,不能总是使用直接访问表。哈希是几乎可以在所有此类情况下使用的解决方案,并且在实践中与上述数据结构(如数组、链表、平衡 BST)相比表现非常出色。(1)搜索时间平均(在合理的假设下)和最坏情况下的 O(n)。现在让我们了解什么是散列。
三、为什么要使用哈希?
3.1 最简单的散列方法
散列:散列是一种流行的技术,用于尽可能快地存储和检索数据。下面用最简单例子说明为什么要散列,如何散列?
比如有0-200的随机数作为key键,那么,如果用全预留表格存储,索引字至少用201个存储单元(有些单元可能永远不用)。
那么我用长度12个长度单元存索引,如下:
Random ∈【0-200】,索引字为Index∈【0,11】,索引字数组长度L=12,模数M=11.
Random % M = Index
给出几个具体数字:55,70,196,185,0,200
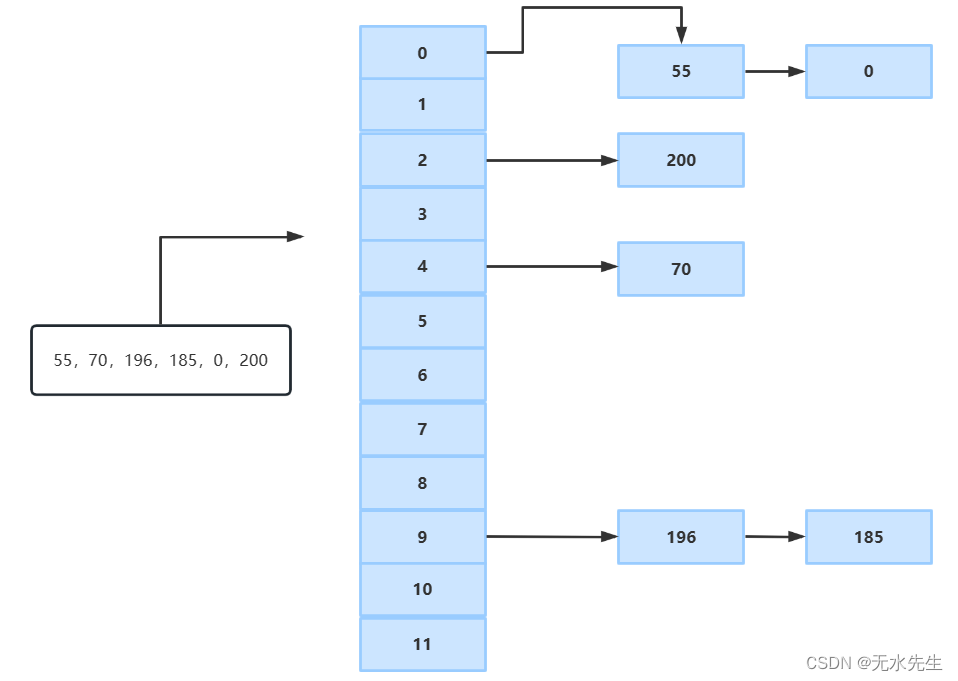
我们索引一个关键字(比如196)的次数为:N = Index(最多10)+ 链表(最多18次)≤ 28次,是不是比全索引表200次要少很多呢?
3.2 更高明的哈希--平恒二叉树
如果你仔细观察,在平衡的二叉搜索树中,如果我们尝试搜索、插入或删除任何元素,那么相同的时间复杂度是 O(logn)。以更快的方式操作,即以更优化的方式和这里的散列开始发挥作用。在散列中,所有上述操作都可以在 O(1) 中执行,即常数时间。重要的是要理解散列的最坏情况时间复杂度仍然是 O(n),但平均情况时间复杂度是 O( 1).
现在让我们了解一些散列的基本操作。
基本操作:
- HashTable:此操作用于创建新的哈希表。
- 删除:此操作用于从哈希表中删除特定的键值对。
- 获取:此操作用于在哈希表中搜索键并返回与该键关联的值。
- Put:此操作用于在哈希表中插入新的键值对。
- DeleteHashTable:此操作用于删除哈希表
3.3 哈希组件
1)哈希表:存储指向与给定电话号码对应的记录的指针的数组。如果没有现有电话号码的哈希函数值等于条目的索引,则哈希表中的条目为 NIL。简单来说,我们可以说哈希表是数组的推广。哈希表提供了一种功能,其中存储数据集合,以便以后在需要时很容易找到这些项目。
2)哈希函数:将给定的大电话号码转换为实用的小整数值的函数。将给定的键转换为特定的槽索引。其主要工作是将每个可能的键映射到唯一的槽索引。如果每个键被映射到一个唯一的槽索引,那么哈希函数被称为完美哈希函数。创建一个完美的哈希函数非常困难,但我们作为程序员的工作是创建这样一个哈希函数,借助它的数量碰撞尽可能少。碰撞在前面讨论。
一个好的哈希函数应该具备以下特性:
- 可高效计算。
- 应该统一分配键(每个表位置每个位置的可能性相同)。
- 应该尽量减少碰撞。
- 应该有一个低负载因子(表中的项目数除以表的大小)。
例如,对于电话号码,一个糟糕的哈希函数是取前三位数字。更好的函数是考虑最后三位数字。请注意,这可能不是最好的哈希函数。
3)冲突处理:由于哈希函数为我们提供了一个大键的小数字,因此有可能两个键产生相同的值。新插入的键映射到哈希表中已被占用的槽的情况称为碰撞和以下是处理冲突的方法:
Chaining:思想是让hash表的每个cell指向一个hash函数值相同的记录链表,Chaining简单,但需要表外额外的内存。
开放式寻址:在开放式寻址中,所有元素都存储在哈希表本身中。每个表条目包含一条记录或 NIL。在搜索元素时,我们逐个检查表槽,直到找到所需的元素或者它是清楚该元素不在表中。
四、结论
知道哈希原理,你就知道快速检索数据库大概是个什么东西,也大概知道,近几年大数据处理的数据库如Redis数据库如何构造。负载平恒概念,dds协议,rtps协议等,理解起来也不复杂了。
相关文章:

【数据管理】谈谈哈希原理和散列表
一、说明 提起哈希,有人要说:不就是一个稀疏表格么,谈的上什么原理?我说:非也,哈希是是那种看似无物,其实解决大问题的东西。如何提高数据管理效率?这是个问题,随着这个问…...

浙江工业大学关于2023年MBA考试初试成绩查询及复试阶段说明
根据往年的情况,2023浙江工业大学MBA考试初试成绩可能将于2月21日公布,为了广大考生可以及时查询到自己的分数,杭州达立易考教育为大家汇总了信息。 1、初试成绩查询:考生可登录中国研究生招生信息网“全国硕士研究生招生考…...

08:进阶篇 - CTK 插件元数据
作者: 一去、二三里 个人微信号: iwaleon 微信公众号: 高效程序员 元数据 元数据用于准确描述一个插件的特征,这样才能让 CTK Plugin Framework 适当地对 Plugin 进行各种处理(例如:依赖解析)。 CTK Plugin Framework 本身提供了一些清单头(元数据属性、条目),在 c…...
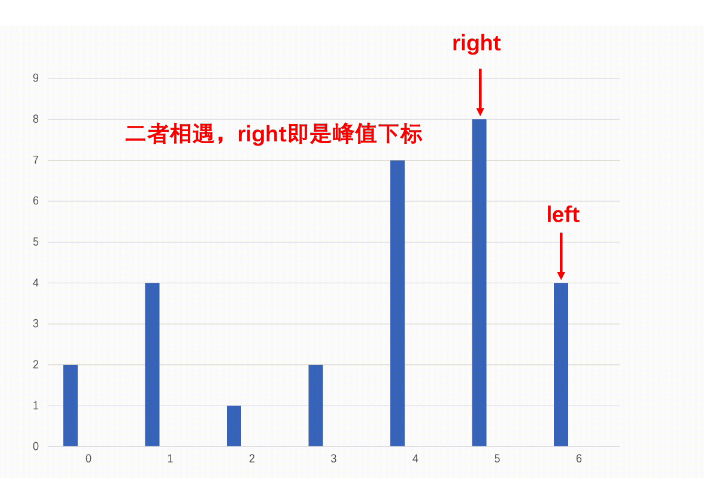
数据结构与算法之数组寻找峰值分而治之
这一篇分享一道在数组中寻找峰值的题目,使用到分而治之,二分查找等思想。本文章会讲解这个二分查找的本质,以及为什么要用二分查找,它能解决哪一类题目?目录:一.题目及其要求1.分而治之2.题目思路3.具体做法…...
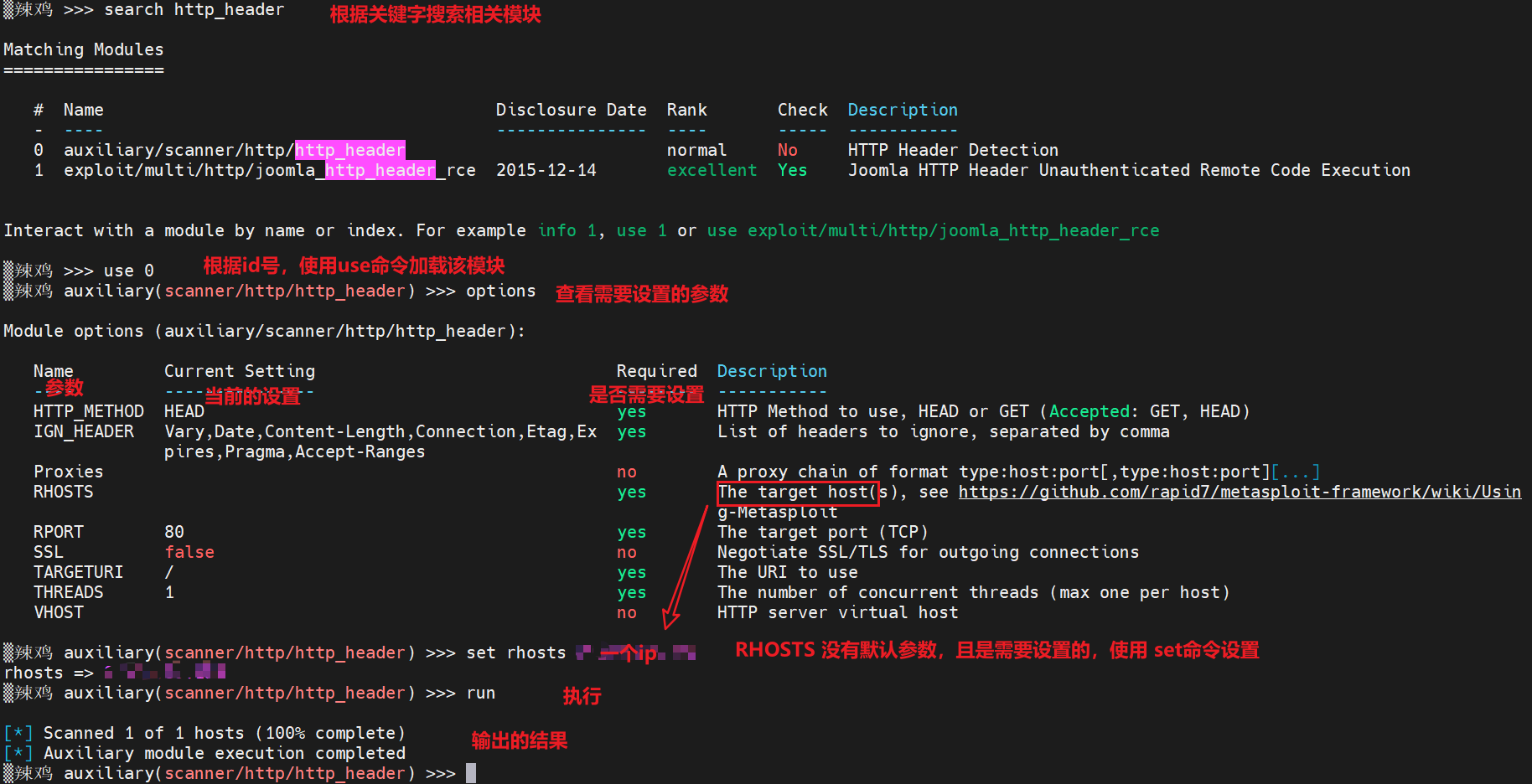
Metasploit 使用篇
文章目录前言一、msfconsole启动msfconsole命令分类核心命令模块命令作业命令资源脚本命令后台数据库命令二、使用案例更改提示和提示字符运行shell命令信息收集:HTTP头检测前言 理解了Meatasploit框架架构、原理之后,自然就很好理解它的使用逻辑 find…...
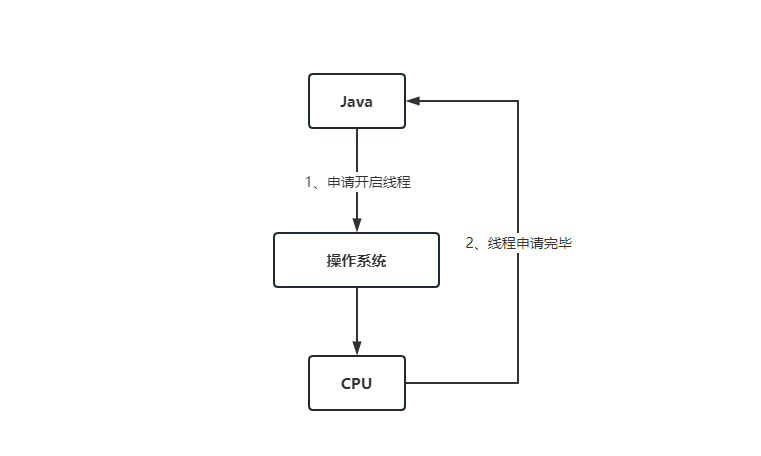
Java岗面试题--Java并发(日积月累,每日三题)
目录面试题一:并行和并发有什么区别?面试题二:线程和进程的区别?追问:守护线程是什么?面试题三:创建线程的几种方式?1. 继承 Thread 类创建线程,重写 run() 方法2. 实现 …...
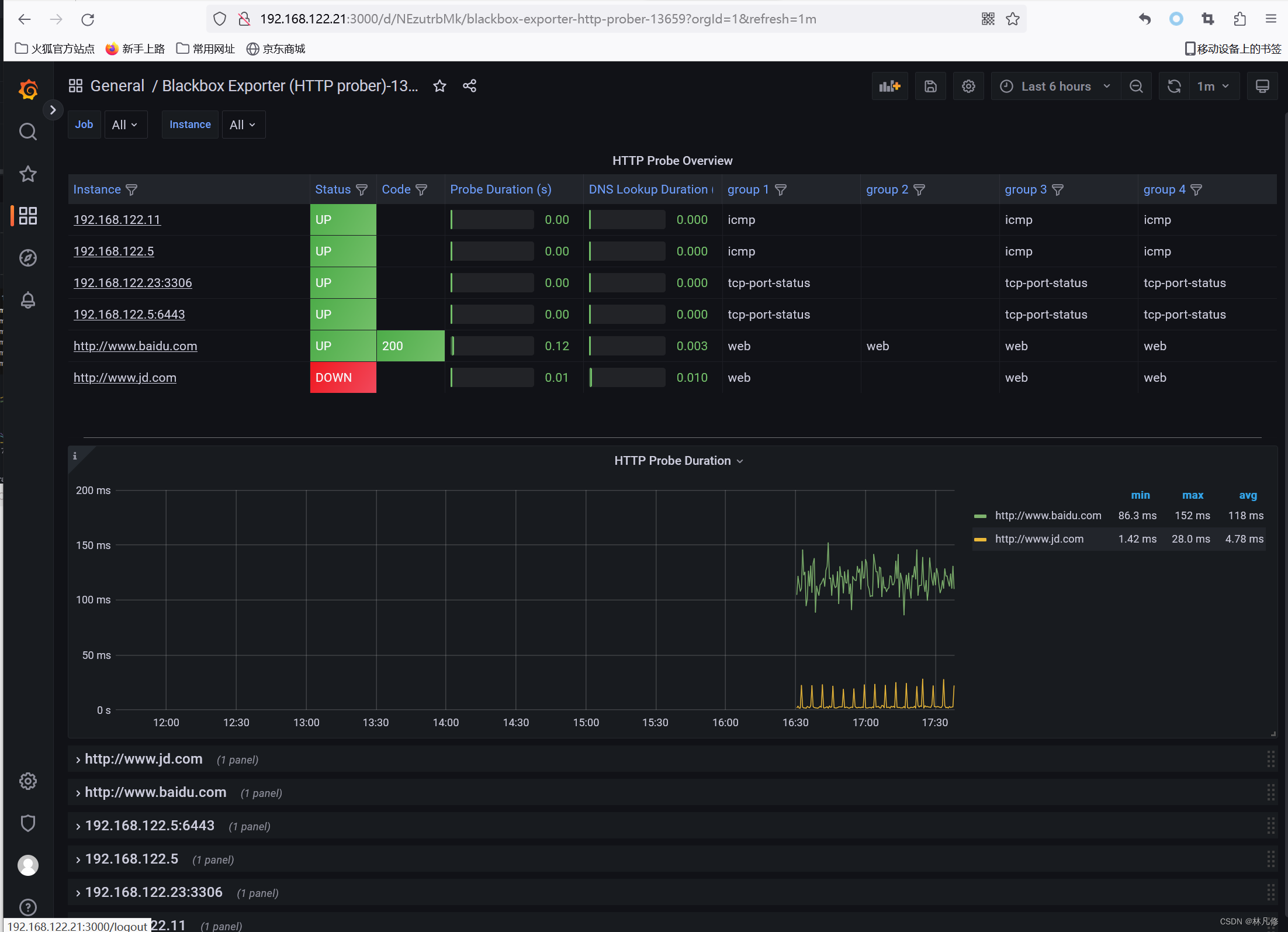
Prometheus监控案例之blackbox-exporter
blackbox-exporter简介 blackbox-exporter项目地址:https://github.com/prometheus/blackbox_exporter blackbox-exporter是Prometheus官方提供的一个黑盒监控解决方案,可以通过HTTP、HTTPS、DNS、ICMP、TCP和gRPC方式对目标实例进行检测。可用于以下使…...

Makefile基础使用和实战详解
Makefile基础使用和实战详解一、基础1.1、简单的Makefile1.2、多文件编译1.3、伪对象.PHONY二、变量2.1、自动变量2.2、特殊变量2.3、变量的类别2.4、变量及其值的来源2.5、变量引用的高级功能2.6、override 指令三、模式四、函数4.1、addprefix 函数4.2、filter函数4.3、filte…...

Go基础-变量
文章目录1 Go中的变量2 声明一个变量3 声明变量并初始化4 变量推断5 声明多个变量5.1 多个变量相同类型5.2 多个变量不同类型6 简短声明7 Go语言变量不能把一种类型赋值给其他类型1 Go中的变量 Go中变量指定了某存储单元的名称,该存储单元会存储特定类型的值&#…...
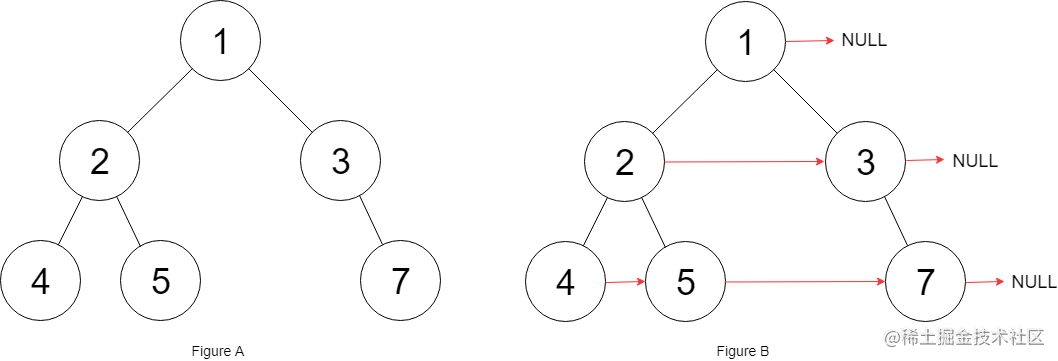
【算法】三道算法题目单词拆分,填充每个节点的下一个右侧节点指针以及组合总和
算法第一道算法题:单词拆分java解答参考第二道算法题:填充每个节点的下一个右侧节点指针java 解答参考第三道算法题:组合总和java解答参考大家好,我是小冷。 今天还是继续学习算法技术知识吧 第一道算法题:单词拆分 …...
)
【算法】刷题路线(系统+全面)
本系列基于当前各大公司对大公司的考察情况,给大家规划一条可行的算法刷题路线,大概会规划 200 道自认为有用的题,并且争取让初学者,能够刷起来更加丝滑,而且每个阶段都会进行相对应的说明。 当然,无论是面…...
Fiddler的报文分析
目录 1.Statistics请求性能数据 2.检测器(Inspectors) 3.自定义响应(AutoResponder) 1.Statistics请求性能数据 报文分析: Request Count: 1 请求数,该session总共发的请求数 Bytes …...

Spring 中,有两个 id 相同的 bean,会报错吗
我们知道,spring容器里面的bean默认是单例的,所以id是唯一的。但是需要注意,同一类型的bean可以有不同的id,比如有id1->bean,也可以有id2->bean。 下面再来详细回答一下文章的问题。 首先,在同一个…...
一查询数据库时间注意点)
Mysql数据库的时间(4)一查询数据库时间注意点
一.select根据时间段查询 1.原始的sql根据时间段查询 select * from stu where time between "1998-09-01" and "1999-09-01"; //查询从1998-09-01到1999-09-01时间段的数据 等同于select * from stu where time >"1998-09-01" and time &l…...

一起学 pixijs(2):修改图形属性
大家好,我是前端西瓜哥。 我们做动画、游戏、编辑器,需要根据用户的交互等操作,去实时地改变图形的属性,比如位置,颜色等信息。今天西瓜哥带大家来看看在 pixijs 怎么修改图形的属性。 因为 pixijs 的底层维护了图形…...

LeetCode 121. 买卖股票的最佳时机
原题链接 难度:easy\color{Green}{easy}easy 题目描述 给定一个数组 pricespricesprices ,它的第 iii 个元素 prices[i]prices[i]prices[i] 表示一支给定股票第 iii 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同…...
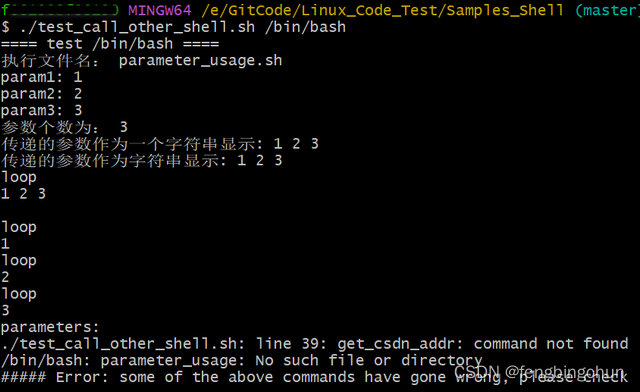
shell脚本内调用另外一个shell脚本的几种方法
有时会在一个shell脚本(如test_call_other_shell.sh)中调用另外一个shell脚本(如parameter_usage.sh),这里总结几种可行的方法,这些方法在linux上和windows上(通过Git Bash)均适用: 1.通过source: 运行在相同的进程,在test_…...

Linux C++ 多进程下write写日志问题思考
文章目录多个进程(父子)同时通过write像日志文件中写,是否会出现数据混乱情况?需要满足以下条件: 1、通过open打开文件,子进程都是复制父进程的文件描述符去操作这个文件,不会造成文件混乱&…...

MySQL的四种事务隔离级别
目录一、事务的基本要素(ACID)1、原子性(Atomicity):2、一致性(Consistency):3、隔离性(Isolation):4、持久性(Durability)…...
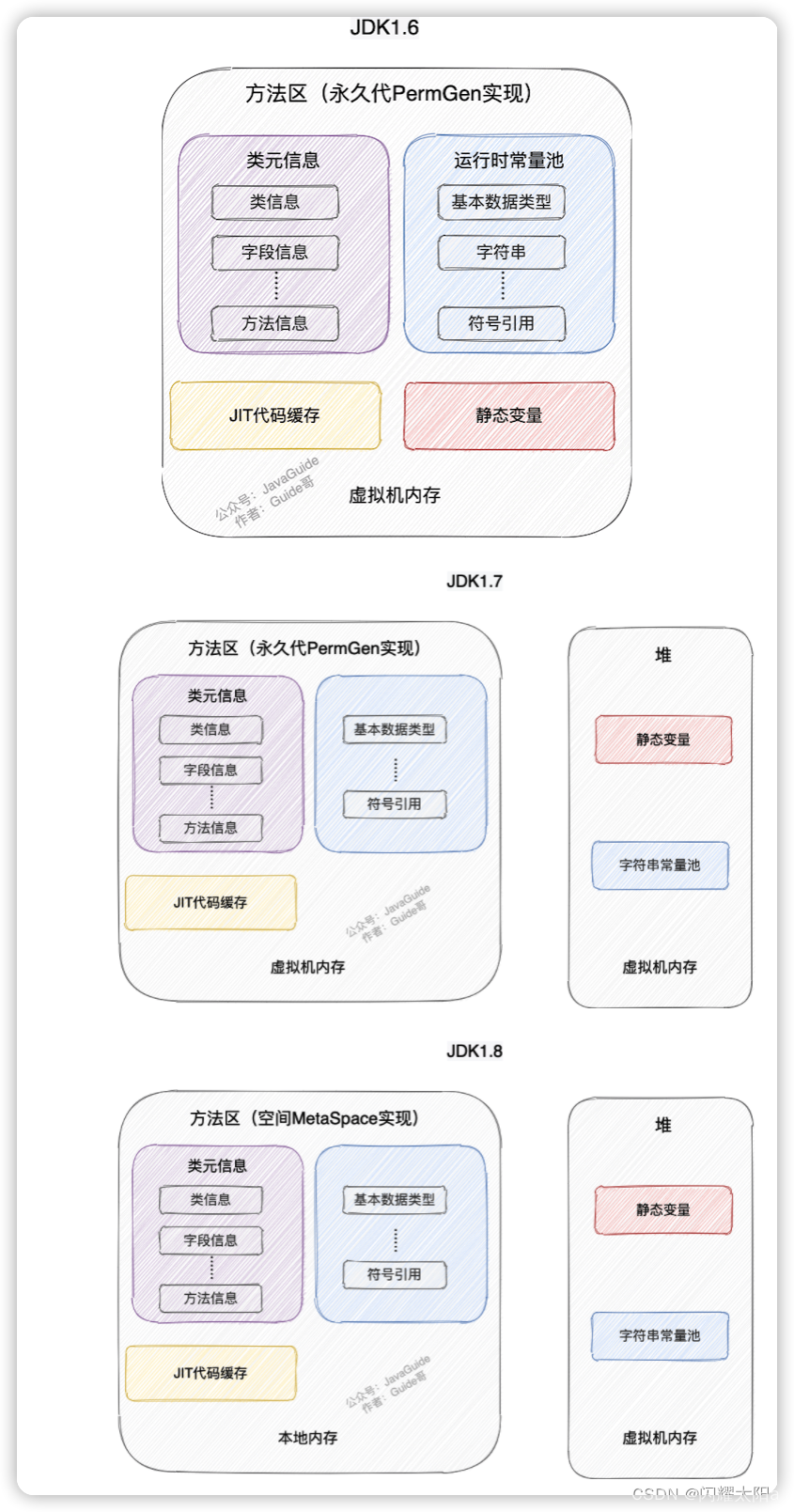
方法区和元空间有什么关系?
一.什么是方法区? 方法区属于是 JVM 运行时数据区域的一块逻辑区域,是各个线程共享的内存区域。 《Java 虚拟机规范》只是规定了有方法区这么个概念和它的作用,方法区到底要如何实现那就是虚拟机自己要考虑的事情了。也就是说,在…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...
