【算法】三道算法题目单词拆分,填充每个节点的下一个右侧节点指针以及组合总和
算法
- 第一道算法题:单词拆分
- java解答参考
- 第二道算法题:填充每个节点的下一个右侧节点指针
- java 解答参考
- 第三道算法题:组合总和
- java解答参考
大家好,我是小冷。
今天还是继续学习算法技术知识吧
第一道算法题:单词拆分
给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict,在字符串中增加空格来构建一个句子,使得句子中所有的单词都在词典中。返回所有这些可能的句子。
说明:
分隔时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。
示例 1:
输入:
s = "
catsanddog
"
wordDict =
[“cat”, “cats”, “and”, “sand”, “dog”]
输出:
[
“cats and dog”,
“cat sand dog”
]
示例 2:
输入:
s = “pineapplepenapple”
wordDict = [“apple”, “pen”, “applepen”, “pine”, “pineapple”]
输出:
[
“pine apple pen apple”,
“pineapple pen apple”,
“pine applepen apple”
]
解释: 注意你可以重复使用字典中的单词。
示例 3:
输入:
s = “catsandog”
wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
输出:
[]
可以根据提示思考
java解答参考
class Solution {public List<String> wordBreak(String s, List<String> wordDict) {List<String> res = new ArrayList<>();int max = 0, min = Integer.MAX_VALUE;Set<String> set = new HashSet<>();for (String word : wordDict) {set.add(word);max = Integer.max(max, word.length());min = Integer.min(min, word.length());}boolean f[] = new boolean[s.length() + 1];f[0] = true;for (int i = 1; i < s.length() + 1; i++) {for (int j = Math.max(i - max, 0); j <= i - min; j++) {if (f[j] && set.contains(s.substring(j, i))) {f[i] = true;break;}}}if (f[s.length()]) {dfs(s, res, new StringBuilder(), set, 0, max, min);}return res;}private void dfs(String s, List<String> res, StringBuilder sb, Set<String> set, int index, int max, int min) {if (index == s.length()) {sb.deleteCharAt(sb.length() - 1);res.add(sb.toString());return;}String str;int size;for (int i = index + min; i <= s.length() && i <= index + max; i++) {if (set.contains(str = s.substring(index, i))) {size = sb.length();sb.append(str).append(' ');dfs(s, res, sb, set, i, max, min);sb.delete(size, sb.length());}}}
}
第二道算法题:填充每个节点的下一个右侧节点指针
给定一个二叉树
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
进阶:
你只能使用常量级额外空间。
使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
示例:
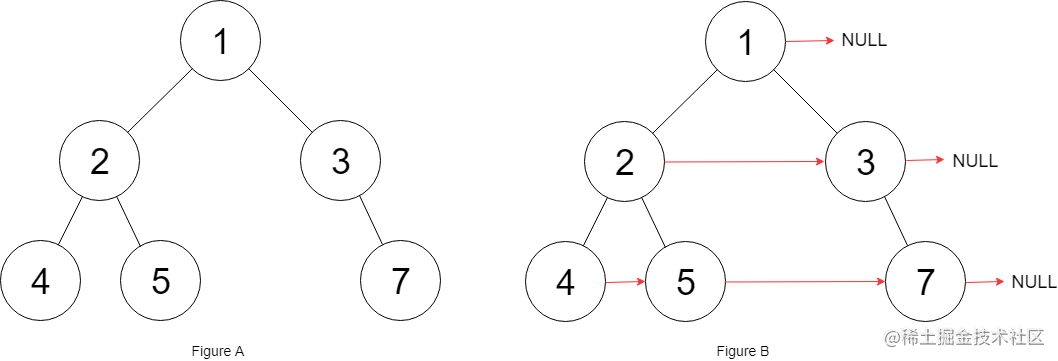
输入:root = [1,2,3,4,5,null,7]
输出:[1,#,2,3,#,4,5,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化输出按层序遍历顺序(由 next 指针连接),‘#’ 表示每层的末尾。
提示:
树中的节点数小于 6000
-100 <= node.val <= 100
java 解答参考
class Node {public int val;public Node left;public Node right;public Node next;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, Node _left, Node _right, Node _next) {val = _val;left = _left;right = _right;next = _next;}
};
class Solution {public Node connect(Node root) {if (root == null || (root.left == null && root.right == null)) {return root;}if (root.left != null && root.right != null) {root.left.next = root.right;root.next = getrightnext(root);}if (root.left != null) {root.left.next = getrightnext(root);}if (root.right != null) {root.right.next = getrightnext(root);}connect(root.right);connect(root.left);return root;}public static Node getrightnext(Node root) {while (root.next != null) {if (root.left != null) {return root.left;}if (root.right != null) {return root.right;}root = root.next;}return null;}
}
第三道算法题:组合总和
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
所有数字(包括 target)都是正整数。
解集不能包含重复的组合。
示例 1:
输入:candidates = [2,3,6,7], target = 7,
输出:[[7],[2,2,3]]
示例 2:
输入:candidates = [2,3,5], target = 8,
输出:[[2,2,2,2],[2,3,3],[3,5]]
提示:
1 <= candidates.length <= 30
1 <= candidates[i] <= 200
candidate 中的每个元素都是独一无二的。
1 <= target <= 500
java解答参考
class Solution {public List<List<Integer>> combinationSum(int[] candiates, int target) {List<List<Integer>> resultList = new ArrayList<>();List<Integer> result = new ArrayList<>();Arrays.sort(candiates);dfs(candiates, resultList, result, 0, target);return resultList;}private void dfs(int[] candiates, List<List<Integer>> resultList, List<Integer> result, int start, int target) {if (target < 0) {return;}else if (target == 0) {resultList.add(new ArrayList<>(result));} else {for (int i = start; i < candiates.length; i++) {result.add(candiates[i]);dfs(candiates, resultList, result, i, target - candiates[i]);result.remove(result.size() - 1);}}}
}
写到最后,小冷一直在技术路上前行…你的关注,评论,收藏都是对我的支持。
昨天,删去;今天,争取;明天,努力。
相关文章:

【算法】三道算法题目单词拆分,填充每个节点的下一个右侧节点指针以及组合总和
算法第一道算法题:单词拆分java解答参考第二道算法题:填充每个节点的下一个右侧节点指针java 解答参考第三道算法题:组合总和java解答参考大家好,我是小冷。 今天还是继续学习算法技术知识吧 第一道算法题:单词拆分 …...
)
【算法】刷题路线(系统+全面)
本系列基于当前各大公司对大公司的考察情况,给大家规划一条可行的算法刷题路线,大概会规划 200 道自认为有用的题,并且争取让初学者,能够刷起来更加丝滑,而且每个阶段都会进行相对应的说明。 当然,无论是面…...
Fiddler的报文分析
目录 1.Statistics请求性能数据 2.检测器(Inspectors) 3.自定义响应(AutoResponder) 1.Statistics请求性能数据 报文分析: Request Count: 1 请求数,该session总共发的请求数 Bytes …...

Spring 中,有两个 id 相同的 bean,会报错吗
我们知道,spring容器里面的bean默认是单例的,所以id是唯一的。但是需要注意,同一类型的bean可以有不同的id,比如有id1->bean,也可以有id2->bean。 下面再来详细回答一下文章的问题。 首先,在同一个…...
一查询数据库时间注意点)
Mysql数据库的时间(4)一查询数据库时间注意点
一.select根据时间段查询 1.原始的sql根据时间段查询 select * from stu where time between "1998-09-01" and "1999-09-01"; //查询从1998-09-01到1999-09-01时间段的数据 等同于select * from stu where time >"1998-09-01" and time &l…...

一起学 pixijs(2):修改图形属性
大家好,我是前端西瓜哥。 我们做动画、游戏、编辑器,需要根据用户的交互等操作,去实时地改变图形的属性,比如位置,颜色等信息。今天西瓜哥带大家来看看在 pixijs 怎么修改图形的属性。 因为 pixijs 的底层维护了图形…...

LeetCode 121. 买卖股票的最佳时机
原题链接 难度:easy\color{Green}{easy}easy 题目描述 给定一个数组 pricespricesprices ,它的第 iii 个元素 prices[i]prices[i]prices[i] 表示一支给定股票第 iii 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同…...
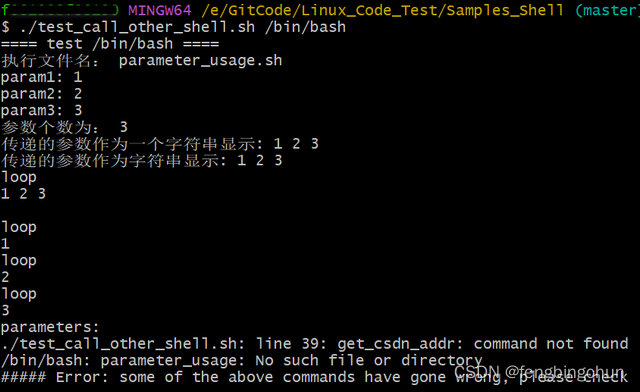
shell脚本内调用另外一个shell脚本的几种方法
有时会在一个shell脚本(如test_call_other_shell.sh)中调用另外一个shell脚本(如parameter_usage.sh),这里总结几种可行的方法,这些方法在linux上和windows上(通过Git Bash)均适用: 1.通过source: 运行在相同的进程,在test_…...

Linux C++ 多进程下write写日志问题思考
文章目录多个进程(父子)同时通过write像日志文件中写,是否会出现数据混乱情况?需要满足以下条件: 1、通过open打开文件,子进程都是复制父进程的文件描述符去操作这个文件,不会造成文件混乱&…...

MySQL的四种事务隔离级别
目录一、事务的基本要素(ACID)1、原子性(Atomicity):2、一致性(Consistency):3、隔离性(Isolation):4、持久性(Durability)…...
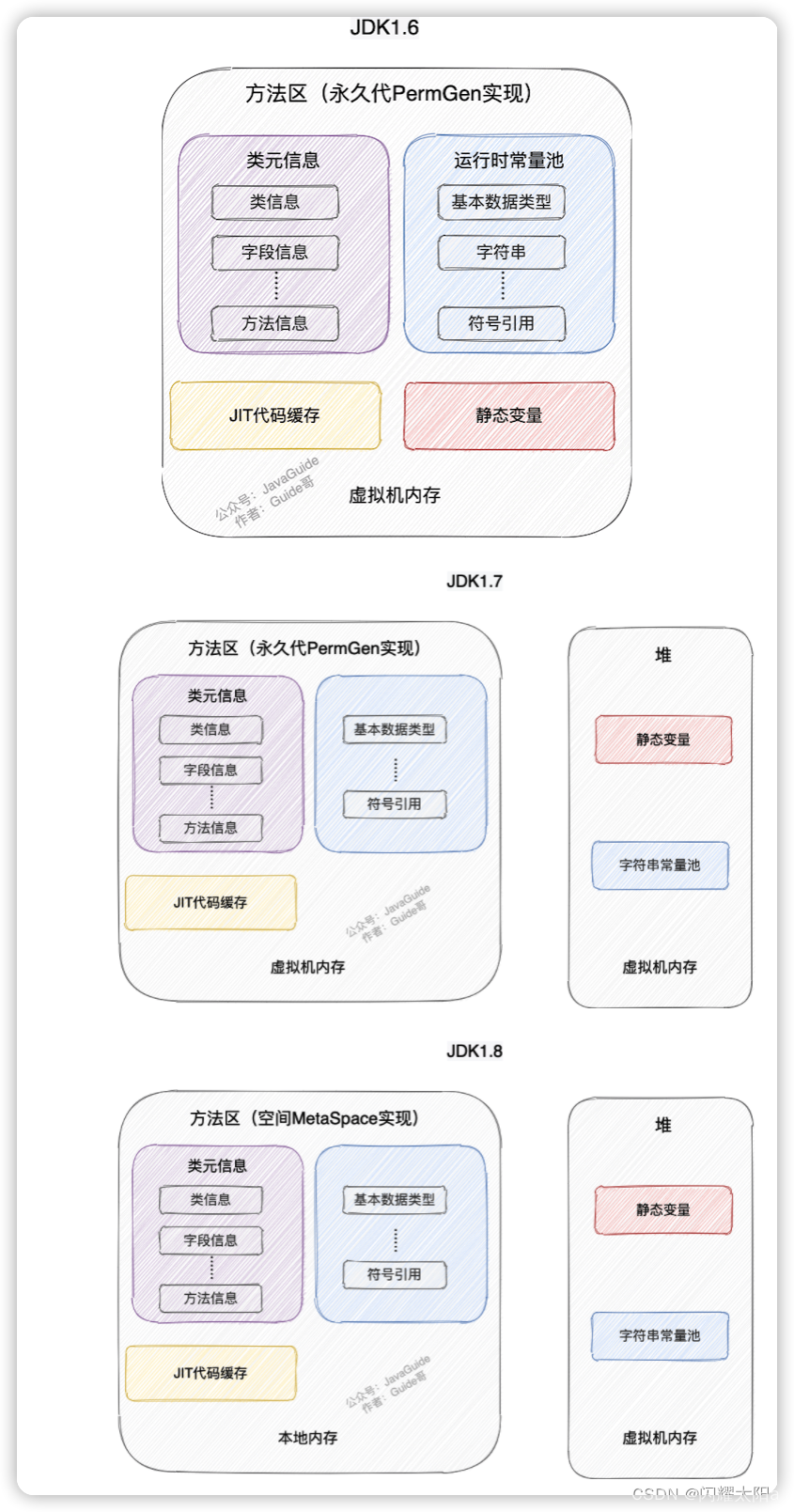
方法区和元空间有什么关系?
一.什么是方法区? 方法区属于是 JVM 运行时数据区域的一块逻辑区域,是各个线程共享的内存区域。 《Java 虚拟机规范》只是规定了有方法区这么个概念和它的作用,方法区到底要如何实现那就是虚拟机自己要考虑的事情了。也就是说,在…...
2023VNCTF的两道(暂时)
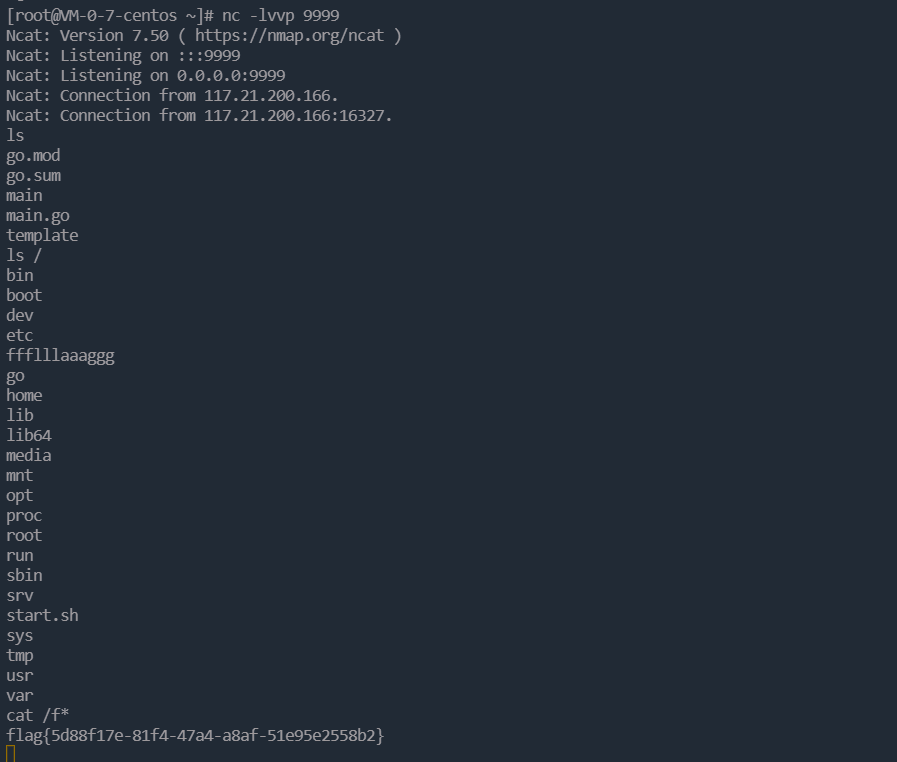
from http://v2ish1yan.top/2023/02/19/%E6%AF%94%E8%B5%9Bwp/2023vnctf/ 比赛的时候在回学校的路上,所以没有打,听说质量挺高,赛后做一下 象棋王子 一个普通的js游戏,玩过关了就给flag,所以flag肯定在前端源码里 这…...

JDK版本区别
1. 泛型 ArrayList listnew ArrayList()------>ArrayList<Integer>listnew ArrayList<Integer>(); 2 自动装箱/拆箱 nt ilist.get(0).parseInt();-------->int ilist.get(0);原始类型与对应的包装类不用显式转换 3 for-each i0;i<a.length;i------------&…...
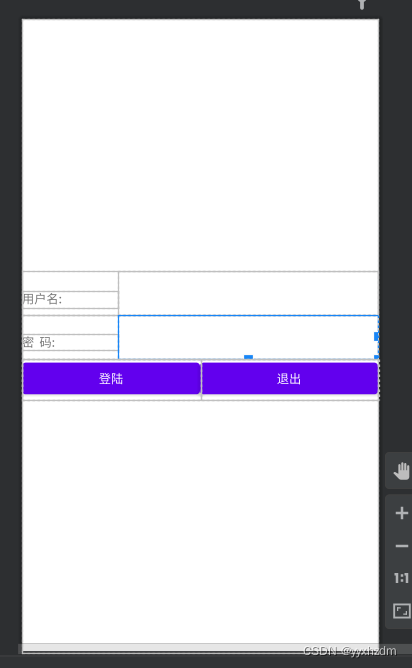
Android 基础知识4-2.8 TableLayout(表格布局)详解
一、TableLayout的概述 表格布局是以行数和列数来确定位置进行排列。就像一间教室,确定好行数与列数就能让同学有序入座。 注意:我们需要先添加<TableRow容器,每添加一个就会多一行,然后再往<TableRow容器中添加其它组件。…...

SQL代码编码原则和规范
目录1、先了解MySQL的执行过程2、数据库常见规范3、所有表必须使用Innodb存储引擎4、每个Innodb表必须有个主键5、数据库和表的字符集统一使用UTF86、查询SQL尽量不要使用select *,而是具体字段7、避免在where子句中使用 or 来连接条件8、尽量使用数值替代字符串类型…...

【博客627】gobgp服务无损变更:graceful restart特性
gobgp服务无损变更:graceful restart特性 场景 当我们的bgp网关在对外宣告bgp路由的时候,如果我们网关有新的特性要发布,那么此时如果把网关停止再启动新版本,此时bgp路由会有短暂撤回再播出的过程,会有网络抖动 期待…...

一起学 pixijs(1):常见图形的绘制
大家好,我是前端西瓜哥。 pixijs 是一个强大的 Web Canvas 2D 库,以其强大性能而著称。其底层使用了 WebGL 实现了硬件加速,当然如果不支持的话,也能回退为 Canvas。 本文使用的 pixijs 版本为 7.1.2。 Application Applicati…...
2023年PMP考试教材有哪些?(含pmp资料)
PMP考试教材是《PMBOK指南》,但这次的考试因为大纲的更新,而需要另外的敏捷书籍来备考。且官方发了通知,3、5月还是第六版指南,8月及8月之后,使用第七版教材。 新版考纲将专注于以下三个新领域: 人 – 强调与有效领导项…...
centos7防火墙工具firewall-cmd使用
centos7防火墙工具firewall-cmd使用防火墙概述centos7防火墙工具firewall-cmd使用介绍firewalld的基本使用服务管理工具相关指令配置firewalld-cmd防火墙概述 防火墙是可以帮助计算机在内部网络和外部网络之间构建一道相对隔绝的保护屏障,从而保护数据信息的一种技…...

js html过滤所有标签格式并清除所有nbsp;
var odiv document.getElementsByTagName("*"); for(var i 0; i<odiv.length; i){ if(odiv[i].className newDetail){ let obj odiv[i].childNodes[3]; let oldHtml odiv[i].childNodes[3].innerText;//获取html中不带标签内容 //console.log(odiv[i].childN…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...
