华为OD机试 - 射击比赛（Python）
射击比赛
题目
给定一个射击比赛成绩单
包含多个选手若干次射击的成绩分数
请对每个选手按其最高三个分数之和进行降序排名
输出降序排名后的选手 ID 序列
条件如下:
- 一个选手可以有多个射击成绩的分数 且次序不固定
- 如果一个选手成绩小于三个 则认为选手的所有成绩无效 排名忽略该选手
- 如果选手的成绩之和相等,则成绩相等的选手按照其 ID 降序排列
输入
输入第一行:一个整数 N
表示该场比赛总共进行了N次射击
产生N个成绩分数 2 <= N <= 100
输入第二行 一个长度为N的整数序列
表示参与本次射击的选手 Id
0 <= ID <= 99
输入第三行是长度为N的整数序列
表示参与每次射击的选手对应的成绩
0 <= 成绩 <= 100
输出
符合题设条件的降序排名后的选手 ID 序列
示例一
输入
13
3,3,7,4,4,4,4,7,7,3,5,5,5
53,80,68,24,39,76,66,16,100,55,53,80,55
输出
5,3,7,4
相关文章：
华为OD机试 - 射击比赛（Python）
射击比赛 题目 给定一个射击比赛成绩单 包含多个选手若干次射击的成绩分数 请对每个选手按其最高三个分数之和进行降序排名 输出降序排名后的选手 ID 序列 条件如下: 一个选手可以有多个射击成绩的分数 且次序不固定如果一个选手成绩小于三个 则认为选手的所有成绩无效 排名忽…...
uniapp自定义验证码输入框，隐藏光标
一. 前言 先看下使用场景效果图： 点击输入框唤起键盘，蓝框就相当于input的光标，验证码输入错误或者不符合格式要求会将字体以及边框改成红色提示，持续1s，然后清空数据，恢复原边框样式；5位验证…...
基于SSM框架的生活论坛系统的设计与实现
基于SSM框架的生活论坛系统的设计与实现 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背景…...
spring注解使用中常见的概念性问题
Spring注解使用中常见的概念性问题Configuration有什么用？Configuration和XML有什么区别？哪种好？Autowired 、 Inject、Resource 之间有什么区别？Value、PropertySource 和 Configuration？Spring如何处理带Configurati…...
Module理解及使用
ES6的模块化设计思想是静态化，也就是说，在编译的时候确定模块的依赖关系，以及输出输出入的变量。而CommonJS和AMD模块都是在运行时确定的。ES6的模块不是对象，而是通过export显示指定输出的代码，再通过import命令输入。…...
ngix 常用配置之 location 匹配规则
大家好，我是 17。 今天和大家详细聊聊 nginx 的 location 匹配规则 location 匹配规则 匹配规则在后面的 try_files 中有举例 location 按如下优先级匹配 绝对匹配，一个字符也不能差^~ 前缀匹配~（区分大小写）， ~*(不…...
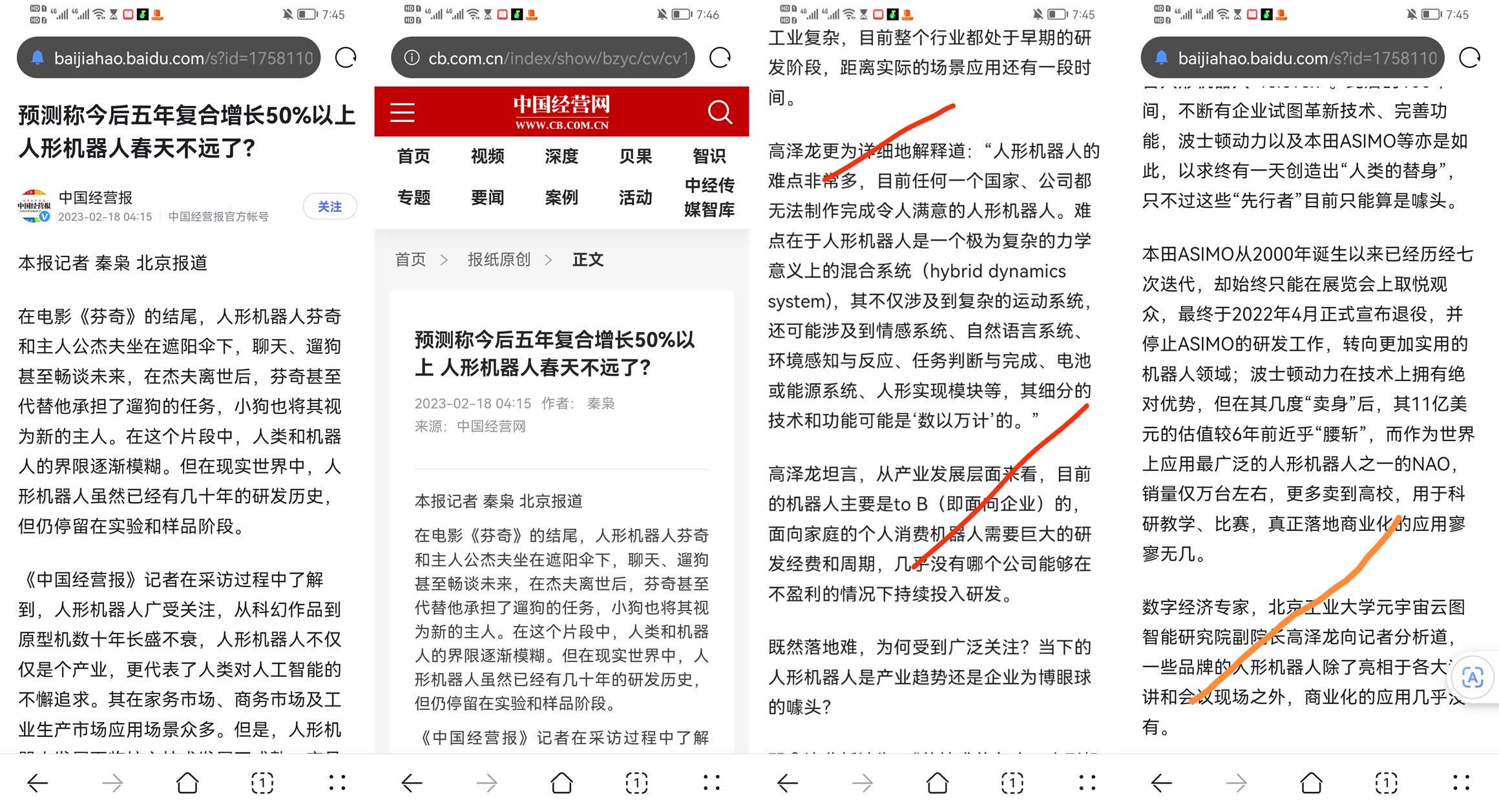
chatGPT与人形机器人，高泽龙接受中国经营报采访谈二者发展
1.相较于Chatgpt，人形机器人的市场前景有多大？答：人形机器人的市场前景可以用“无限大”来形容，这看起来很夸张而且并不合理，其实是客观而且中肯的。因为这个问题就仿佛是五十年前，人们问“未来的电脑市场有…...
进程同步——读者-写者问题
读者-写者问题 互斥制约与合作制约双重关系的进程同步问题描述是： 一个被多个进程共享的文件、记录或数据结构，允许进程对其执行读、写操作。读进程称为读者，写进程称为写者。其允许多个进程同时读取，但只要有一个进程在读&#…...
Android自动化配置
1 搭建APPIUM环境 1.1 安装node.js Appium是使用nodejs实现的，所以node是解释器，需要第一步安装好 node.js的安装包下载地址： https://nodejs.org/en/download/ 注意：node.js的安装包的下载在官网有两种版本，建议大…...
Java程序怎么运行？final、static用法小范围类型转大范围数据类型可以吗？
文章目录1.能将int强制转换为byte类型的变量吗？如果该值大于byte类型的范围，将会出现什么现象？2. Java程序是如何执行的？3.final 在 Java 中有什么作用？4.final有哪些用法?5.static都有哪些用法?1.能将int强制转换为…...
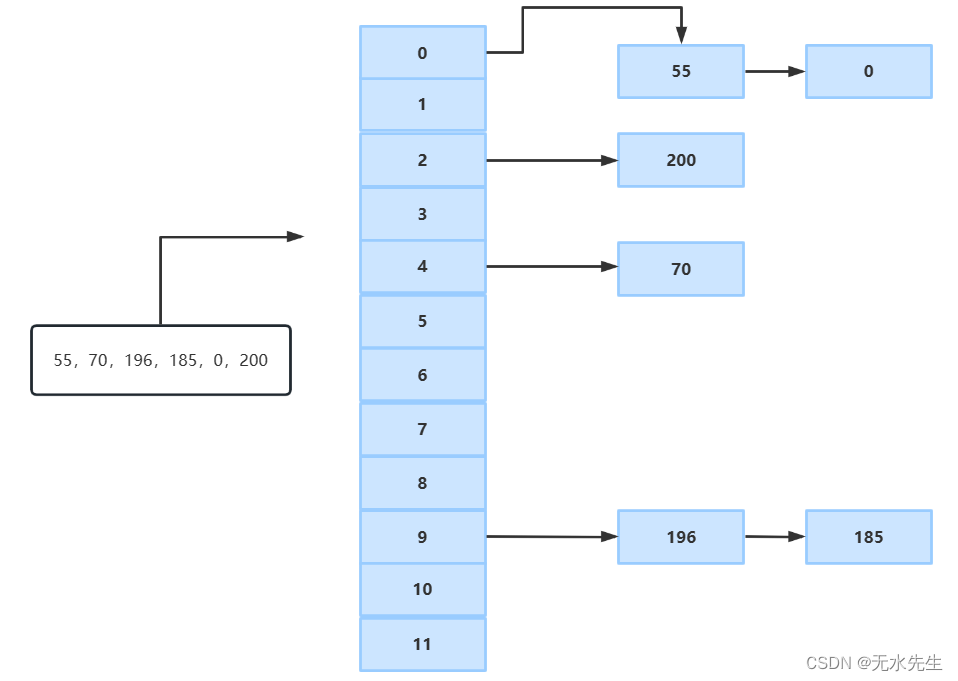
【数据管理】谈谈哈希原理和散列表
一、说明 提起哈希，有人要说：不就是一个稀疏表格么，谈的上什么原理？我说：非也，哈希是是那种看似无物，其实解决大问题的东西。如何提高数据管理效率？这是个问题，随着这个问…...
浙江工业大学关于2023年MBA考试初试成绩查询及复试阶段说明
根据往年的情况，2023浙江工业大学MBA考试初试成绩可能将于2月21日公布，为了广大考生可以及时查询到自己的分数，杭州达立易考教育为大家汇总了信息。 1、初试成绩查询：考生可登录中国研究生招生信息网“全国硕士研究生招生考…...
08：进阶篇 - CTK 插件元数据
作者： 一去、二三里 个人微信号： iwaleon 微信公众号： 高效程序员 元数据 元数据用于准确描述一个插件的特征，这样才能让 CTK Plugin Framework 适当地对 Plugin 进行各种处理（例如：依赖解析）。 CTK Plugin Framework 本身提供了一些清单头（元数据属性、条目），在 c…...
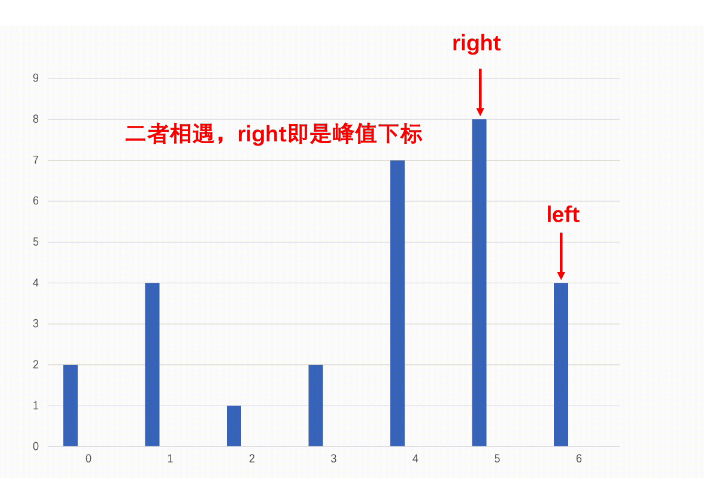
数据结构与算法之数组寻找峰值分而治之
这一篇分享一道在数组中寻找峰值的题目，使用到分而治之，二分查找等思想。本文章会讲解这个二分查找的本质，以及为什么要用二分查找，它能解决哪一类题目？目录：一.题目及其要求1.分而治之2.题目思路3.具体做法…...
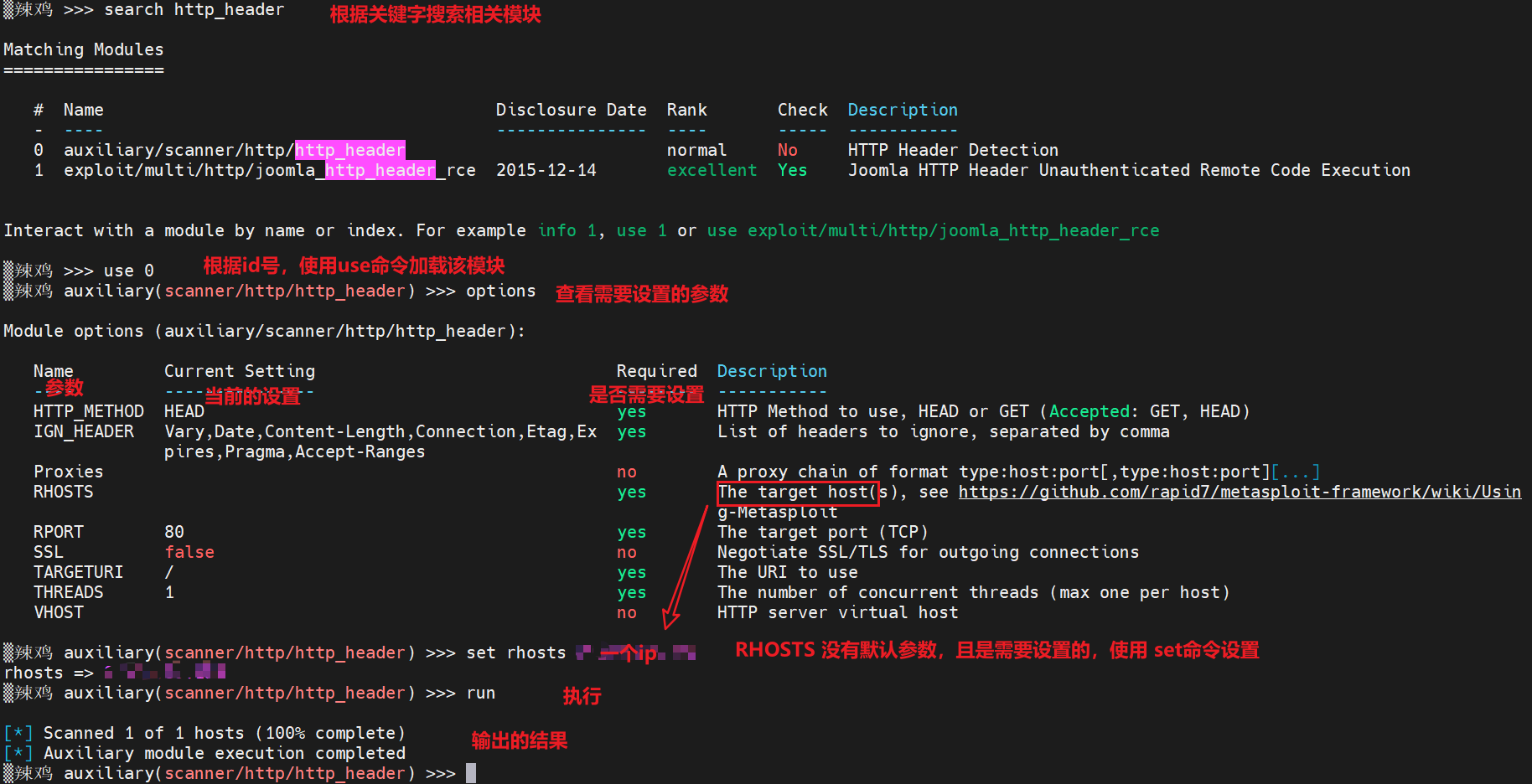
Metasploit 使用篇
文章目录前言一、msfconsole启动msfconsole命令分类核心命令模块命令作业命令资源脚本命令后台数据库命令二、使用案例更改提示和提示字符运行shell命令信息收集：HTTP头检测前言 理解了Meatasploit框架架构、原理之后，自然就很好理解它的使用逻辑 find…...
Java岗面试题--Java并发（日积月累，每日三题）
目录面试题一：并行和并发有什么区别？面试题二：线程和进程的区别？追问：守护线程是什么？面试题三：创建线程的几种方式？1. 继承 Thread 类创建线程，重写 run() 方法2. 实现 …...
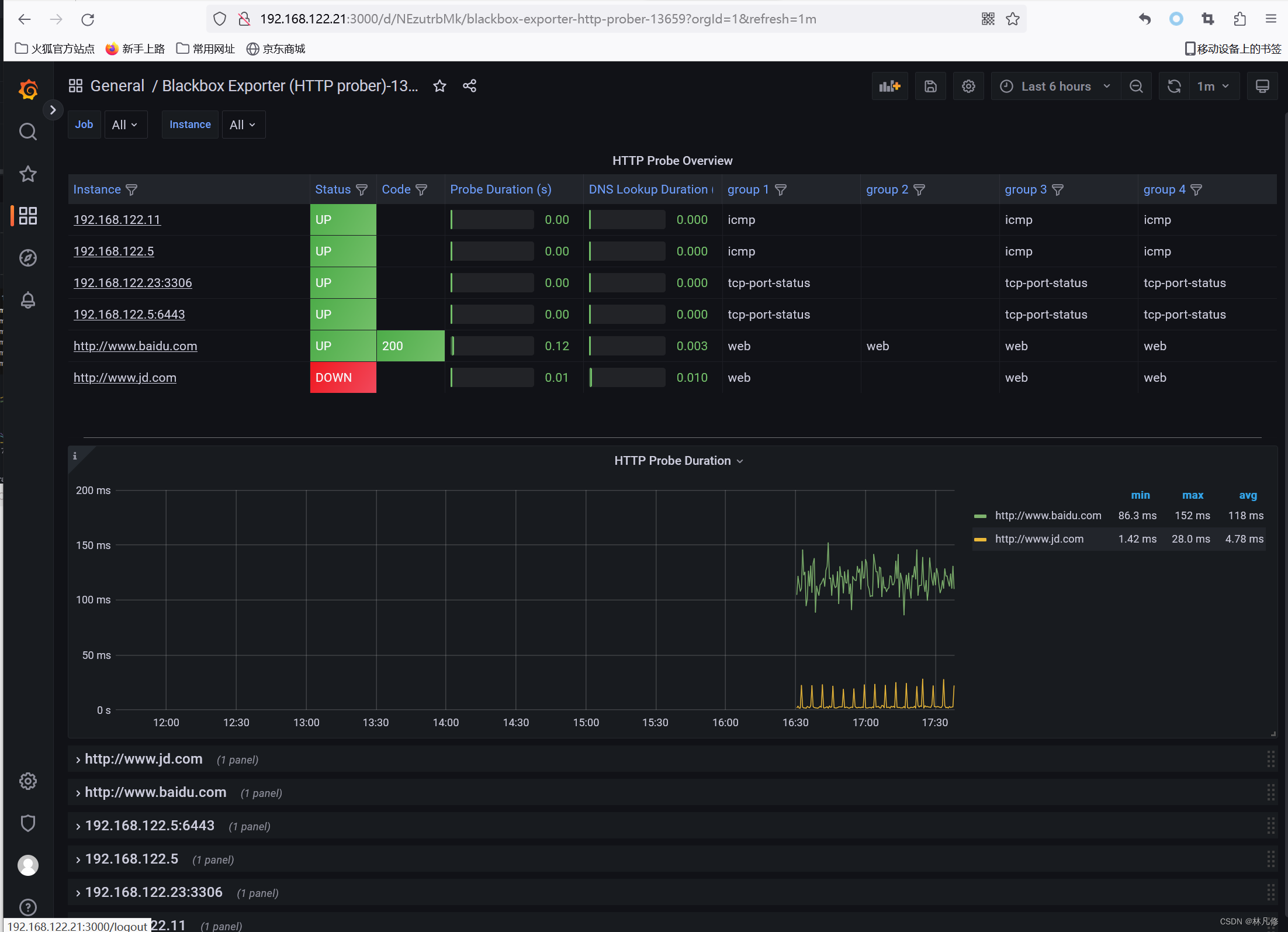
Prometheus监控案例之blackbox-exporter
blackbox-exporter简介 blackbox-exporter项目地址：https://github.com/prometheus/blackbox_exporter blackbox-exporter是Prometheus官方提供的一个黑盒监控解决方案，可以通过HTTP、HTTPS、DNS、ICMP、TCP和gRPC方式对目标实例进行检测。可用于以下使…...
Makefile基础使用和实战详解
Makefile基础使用和实战详解一、基础1.1、简单的Makefile1.2、多文件编译1.3、伪对象.PHONY二、变量2.1、自动变量2.2、特殊变量2.3、变量的类别2.4、变量及其值的来源2.5、变量引用的高级功能2.6、override 指令三、模式四、函数4.1、addprefix 函数4.2、filter函数4.3、filte…...
Go基础-变量
文章目录1 Go中的变量2 声明一个变量3 声明变量并初始化4 变量推断5 声明多个变量5.1 多个变量相同类型5.2 多个变量不同类型6 简短声明7 Go语言变量不能把一种类型赋值给其他类型1 Go中的变量 Go中变量指定了某存储单元的名称，该存储单元会存储特定类型的值&#…...
【算法】三道算法题目单词拆分，填充每个节点的下一个右侧节点指针以及组合总和
算法第一道算法题：单词拆分java解答参考第二道算法题：填充每个节点的下一个右侧节点指针java 解答参考第三道算法题：组合总和java解答参考大家好，我是小冷。 今天还是继续学习算法技术知识吧 第一道算法题：单词拆分 …...
大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动（如演唱会、马拉松赛事、高考中考等）期间，城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例，暖城商圈曾因观众集中离场导致周边…...
python爬虫：Newspaper3k 的详细使用（好用的新闻网站文章抓取和解析的Python库）
更多内容请见： 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...
sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...
鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发，使用DevEco Studio作为开发工具，采用Java语言实现，包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定，这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中，积分电荷法最为常用，其原理是通过测量在电容器上积累的热释电电荷，从而确定热释电系数…...
AI病理诊断七剑下天山，医疗未来触手可及
一、病理诊断困局：刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断"，医生需通过显微镜观察组织切片，在细胞迷宫中捕捉癌变信号。某省病理质控报告显示，基层医院误诊率达12%-15%，专家会诊…...
Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ；并安装。 基础操作不再赘述。 打开 macOS 终端，开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
Java编程之桥接模式
定义 桥接模式（Bridge Pattern）属于结构型设计模式，它的核心意图是将抽象部分与实现部分分离，使它们可以独立地变化。这种模式通过组合关系来替代继承关系，从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）
考察一般的三次多项式，以r为参数： p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]； 此多项式的根为： 尽管看起来这个多项式是特殊的，其实一般的三次多项式都是可以通过线性变换化为这个形式…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...