基于PSO-KELM的时间序列数据预测(含对比实验)
前段时间有粉丝私信想让我出一期对时间序列预测的文章,所以今天它来了。

时间序列数据,如股指价格,具有波动性、非线性和突变的特点,对于这类数据的预测往往需要可靠强健的预测模型,而传统的机器学习算法如SVM、BP等,大都采用误差最小化或反向传播来改进预测性能,大量参数调整、复杂的模型架构以及迭代时间长让这些模型逐渐落后。
而极限学习机ELM和核极限学习机KELM能够很好的克服这些问题,作者在前面的文章中介绍了ELM和KELM的原理及其实现,ELM具有训练速度快、复杂度低、克服了传统梯度算法的局部极小、过拟合和学习率的选择不合适等优点,而KELM则利用了核学习的方法,用核映射代替随机映射,能够有效改善隐层神经元随机赋值带来的泛化性和稳定性下降的问题,应用于非线性问题的性能更优[1]。
因此作者将用KELM和ELM结合作者前面提到的优化算法来预测股指的变化,并将之与BP神经网络这类传统机器学习算法进行对比。
00目录
1 PSO-KELM模型
2代码目录
3 预测性能
4 展望
参考文献
01 PSO-KELM模型
1.1 PSO与KELM原理
PSO即粒子群优化算法,KELM即核极限学习机,作者在前面的文章中讲解过其具体原理,文章链接如下,这里不再赘述。
KELM核极限学习机原理及其实现
1.2 样本选取与预处理
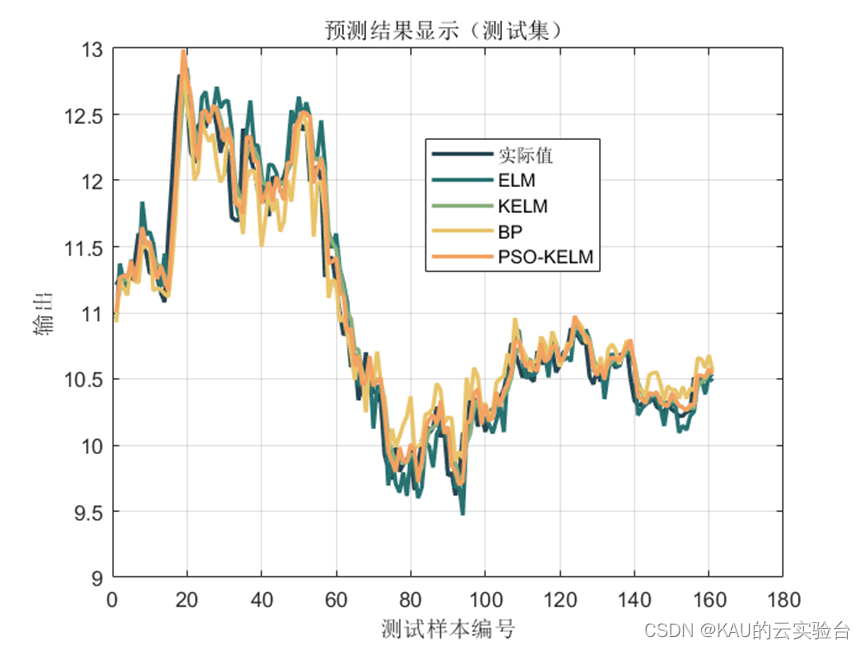
以某股的开盘价作为研究样本,有效数据共554个,考虑用前20日的开盘价预测第21日的开盘价,即以20个数据作为一个样本进行滚动预测,一共可得到534个样本,选取前70%的样本作为训练数据,后30%作为测试数据。
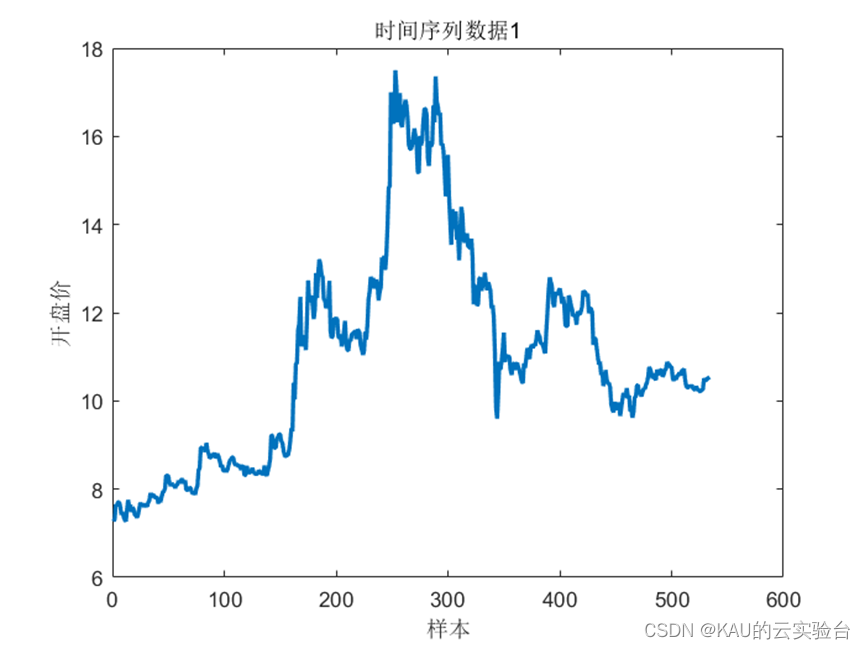
原始数据间差波动范围比较大,会影响模型稳定性和预测精度。因此在把开盘价数据输入之前,首先需要对数据进行预处理即归一化本文对原始数据进行归一化处理,将样本数据处理到区间[0, 1]之间,归一化公式为
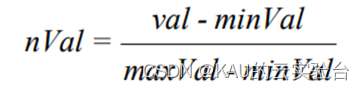
minVal为数据序列中的最小值,maxval为数据序列最大值。
1.3 PSO-KELM预测模型
将PSO与KELM结合,以KELM模型预测的MAE作为PSO的适应度,该模型流程如下:

02 代码目录

其中,MY_XX_Reg.m都是可单独运行的主程序,而result.m用于对比不同算法预测效果,result.m可依次运行4个MY_XX_Reg.m,并对其预测结果进行对比。
03 预测性能
3.1 评价指标
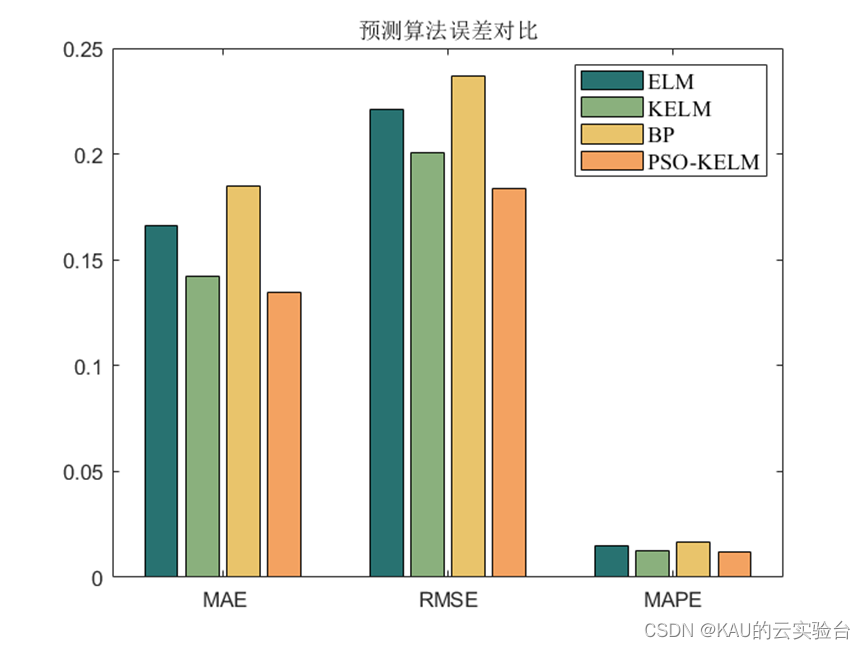
为了验证预测结果的准确性和精度,分别采用均方根差(Root Mean Square Error,RMSE) 、平均绝对百分误差( Mean Absolute Percentage Error,MAPE) 和平均绝对值误差 ( Mean Absolute Error,MAE) 作为评价标准。
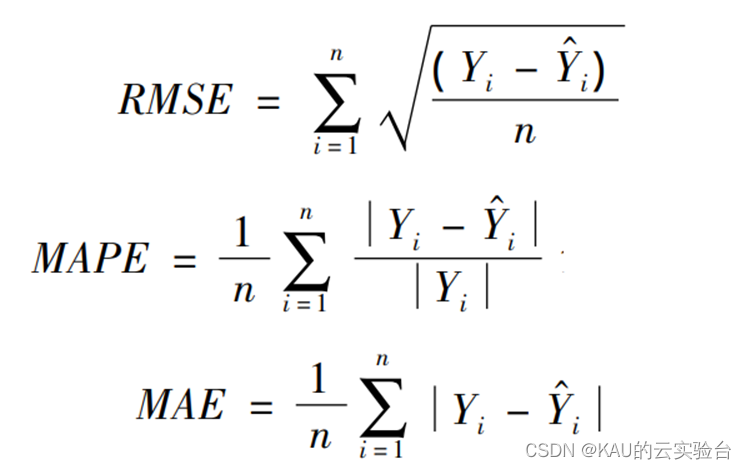
式中 Yi 和Y ^ i分别为真实值和预测值; n 为样本数。
3.2 结果对比
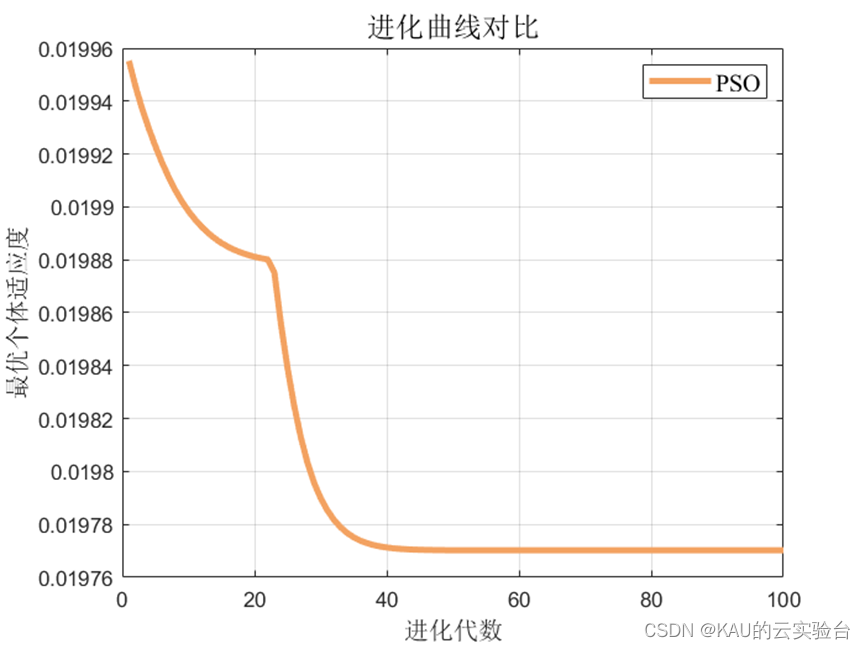
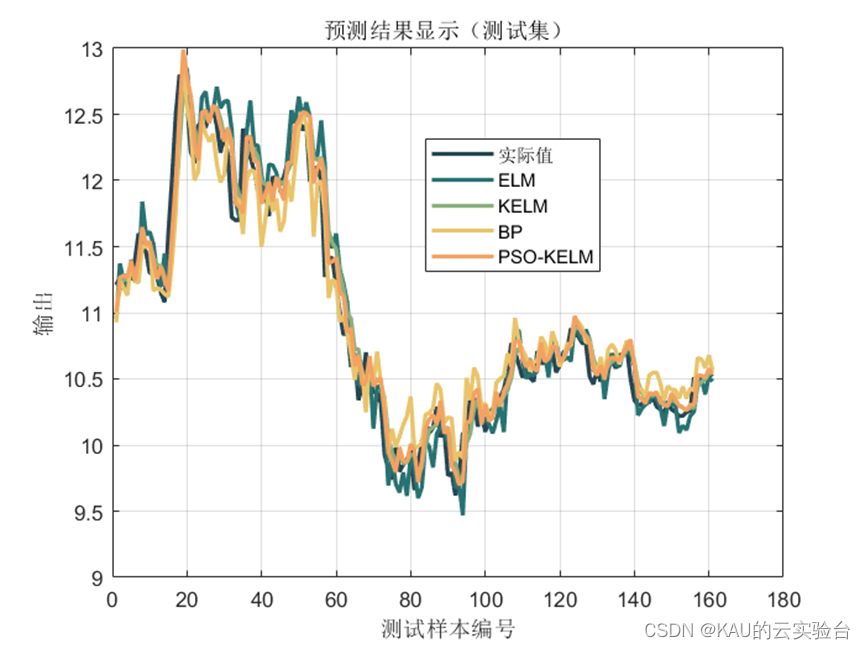

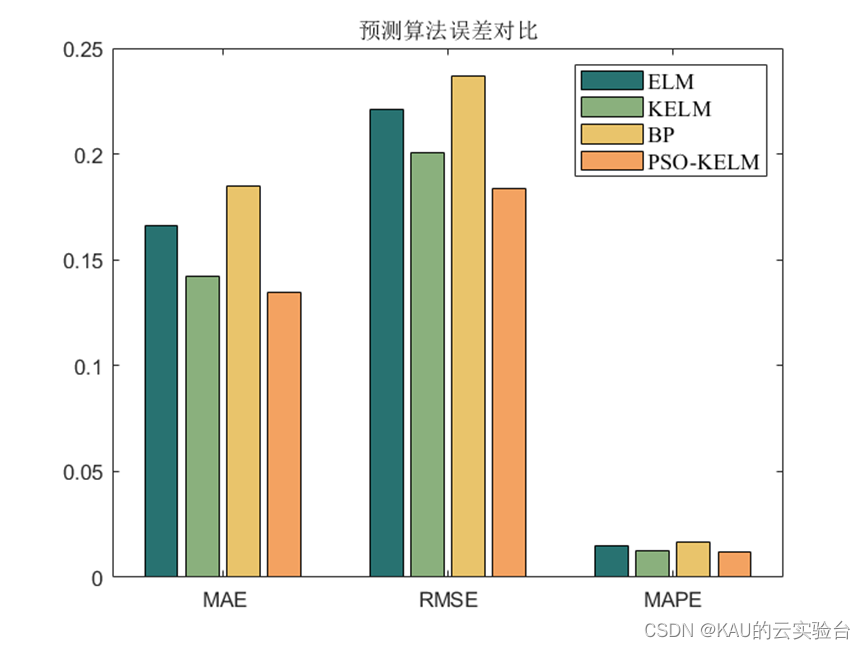
可以看出,预测模型中,经PSO优化后的KELM预测模型取得了不错的效果,同时,也可以引入作者前面提到的各种改进算法提高PSO的寻优性能,以取得更佳的效果
04 展望
在这一篇文章中作者实现了PSO-KELM对于时间序列数据的预测,并对比了ELM和BP。后面作者将介绍蜣螂优化算法及其改进,这也是一位粉丝朋友私信我的,KAU本着有求必应的原则(能力范围内~)给安排了
以上
源码获取
可私信作者
参考文献
[1] Huang G B,Zhou H M,Ding X J,et al.Extreme learning machine for regression and multiclass classification[J].IEEE Transactions on Systems, Man,and Cybernetics,Part B (Cybernetics),2012,42(2):513.
另:如果有伙伴有待解决的优化问题(各种领域都可),可以发我,我会选择性的更新利用优化算法解决这些问题的文章。
如果这篇文章对你有帮助或启发,可以点击右下角的赞/在看(ง •̀_•́)ง(不点也行),若有定制需求,可私信作者。
相关文章:

基于PSO-KELM的时间序列数据预测(含对比实验)
前段时间有粉丝私信想让我出一期对时间序列预测的文章,所以今天它来了。 时间序列数据,如股指价格,具有波动性、非线性和突变的特点,对于这类数据的预测往往需要可靠强健的预测模型,而传统的机器学习算法如SVM、BP等…...

线性代数(二) 矩阵及其运算
前言 行列式det(A) 其实表示的只是一个值 ∣ a b c d ∣ a d − b c \begin{vmatrix} a & b\\ c & d\end{vmatrix} ad -bc acbd ad−bc,其基本变化是基于这个值是不变。而矩阵表示的是一个数表。 定义 矩阵与线性变换的关系 即得 ( a 11 a 12…...

【图像分类】理论篇(4)图像增强opencv实现
随机旋转 随机旋转是一种图像增强技术,它通过将图像以随机角度进行旋转来增加数据的多样性,从而帮助改善模型的鲁棒性和泛化能力。这在训练深度学习模型时尤其有用,可以使模型更好地适应各种角度的输入。 原图像: 旋转后的图像&…...

Centos下的tcpdump抓包用法
先查一下是否安装, 无的话装一下 (版本低的用yum install) : rpm -qa tcpdump dnf install tcpdump 1. 列出能抓包的网卡: tcpdump -D | --list-interfaces 2. 在eth0网卡上抓来源为10.1.1.1 的包, 只抓一个包 (-n这里是不解析DNS) : tcpdump -i eth0 -n src 10.1.1.1 -…...
-[记忆的存储与应用])
自然语言处理从入门到应用——LangChain:记忆(Memory)-[记忆的存储与应用]
分类目录:《自然语言处理从入门到应用》总目录 使用SQLite存储的实体记忆 我们将创建一个简单的对话链,该链使用ConversationEntityMemory,并使用SqliteEntityStore作为后端存储。使用EntitySqliteStore作为记忆entity_store属性上的参数&am…...
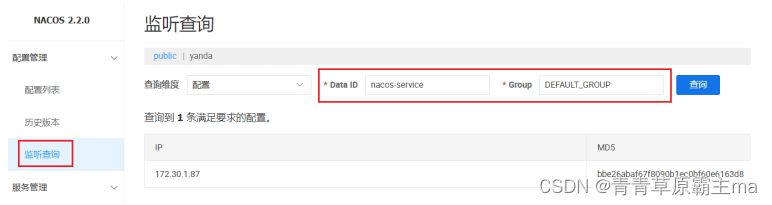
微服务与Nacos概述-5
引入OpenFeign 添加依赖: <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId> </dependency> <dependency><groupId>com.alibaba.cloud</groupId>…...
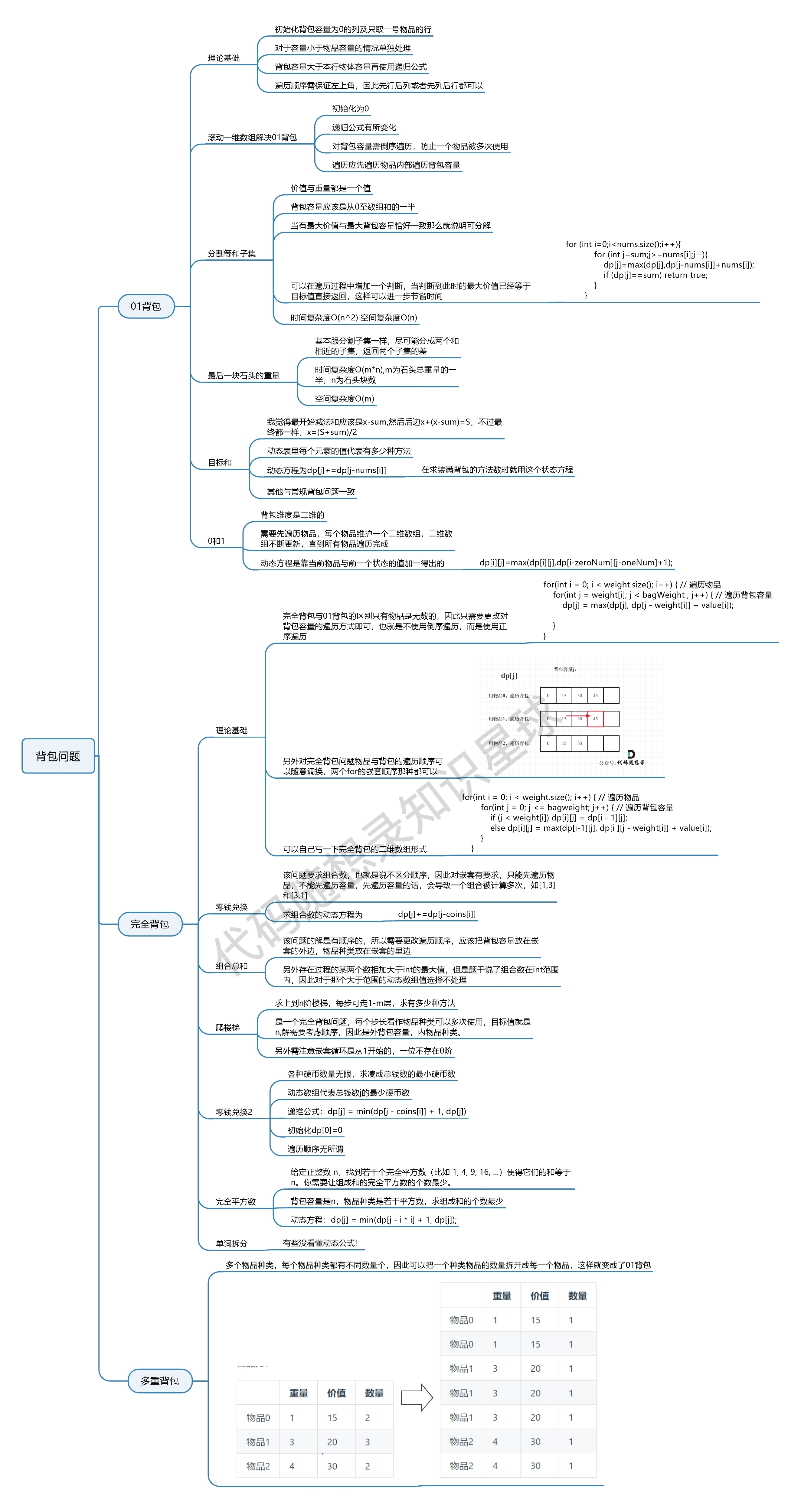
第九章 动态规划part08(代码随想录)
139.单词拆分 1. 确定dp[i][j] dp数组以及下标的含义一维dp数组的递推公式 dp[i] : 字符串长度为i的话,dp[i]为true,表示可以单词能被在字典中出现的单词组成。 dp[s.size()] true; 说明可以利用字典中出现的单词拼接出 s 。 2. 一维dp数组的递推公式…...
---工厂模式实现灯光控制(继电器组)以及火灾报警模组的封装)
智能家居(1)---工厂模式实现灯光控制(继电器组)以及火灾报警模组的封装
采用工厂模式以面向对象的方式来封装各种设备模块,方便整合项目以及后期的维护和扩展 mainPro.c(主函数) #include <stdio.h> #include "controlDevice.h"struct Devices *pdeviceHead NULL; //设备工厂链…...
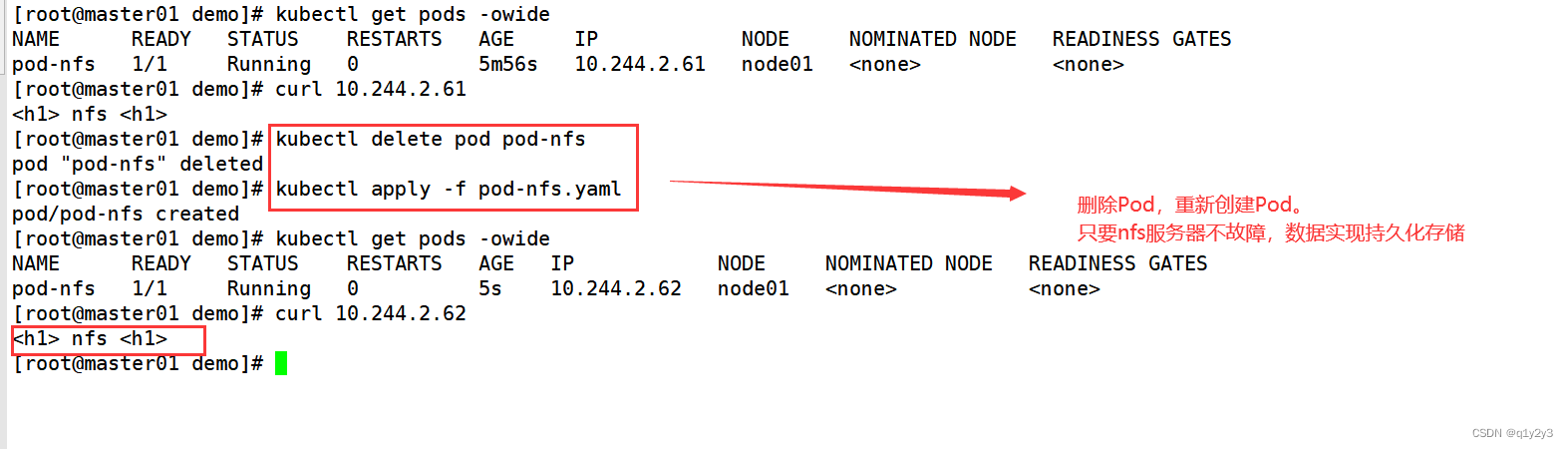
kubernetes的存储卷使用
目录 一、为什么使用存储卷 二、emptyDir存储卷 1.概念 2.创建Pod emptyDir 3. 验证emptyDir存储卷 三、hostPath存储卷 1.概念 2.创建Pod hostPath 3.验证hostPath存储卷 三、nfs共享存储卷 1.概念 2.安装nfs,配置nfs服务 3.创建Pod 4.验证nfs存储卷 一、…...

centos 之安装 openssl 1.1.1报错
源码make时报错,可能是系统的perl的版本太低问题。 [rootlocalhost ~]# cpan -a | grep Test::More Test::More 0.92 1.302171 EXODIST/Test-Simple-1.302171.tar.gz [rootlocalhost ~]# cpan -a | grep Text::Template [rootlocalhost ~]# …...
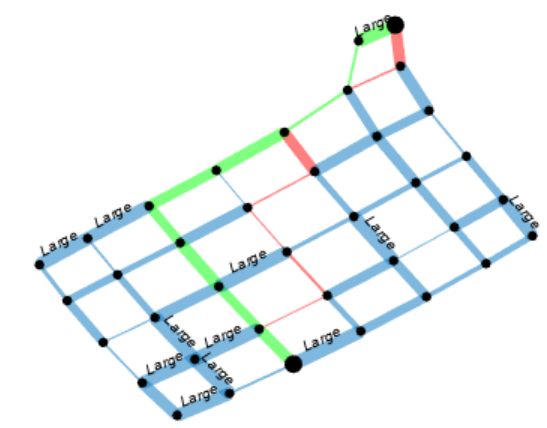
matlab使用教程(16)—图论中图的定义与修改
1.修改现有图的节点和边 此示例演示如何使用 addedge 、 rmedge 、 addnode 、 rmnode 、 findedge 、 findnode 及 subgraph 函数访问和修改 graph 或 digraph 对象中的节点和/或边。 1.1 添加节点 创建一个包含四个节点和四条边的图。s 和 t 中的对应元素用于指定每条…...

【C++面向对象】--- 继承 的奥秘(下篇)
个人主页:平行线也会相交💪 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创 收录于专栏【C之路】💌 本专栏旨在记录C的学习路线,望对大家有所帮助🙇 希望我们一起努力、成长&…...
Android 面试笔记整理-Binder机制
作者:浪人笔记 面试可能会问到的问题 从IPC的方式问到Binder的优势为什么zygote跟其他服务进程的通讯不使用BinderBinder线程池和Binder机制 等等这些问题都是基于你对Binder的理解还有对其他IPC通讯的理解 IPC方式有多少种 传统的IPC方式有Socket、共享内存、管道…...
编程小白的自学笔记十三(python办公自动化读写文件)
系列文章目录 编程小白的自学笔记十二(python爬虫入门四Selenium的使用实例二) 编程小白的自学笔记十一(python爬虫入门三Selenium的使用实例详解) 编程小白的自学笔记十(python爬虫入门二实例代码详解)…...
【Mariadb高可用MHA】
目录 一、概述 1.概念 2.组成 3.特点 4.工作原理 二、案例介绍 1.192.168.42.3 2.192.168.42.4 3.192.168.42.5 4.192.168.42.6 三、实际构建MHA 1.ssh免密登录 1.1 所有节点配置hosts 1.2 192.168.42.3 1.3 192.168.42.4 1.4 192.168.42.5 1.5 192.168.42.6 …...

网络五层协议
应用层(http,https),传输层(udp,tcp),网络层(ip),数据链路层,物理层 什么是http?http 与https 的区别_日晞的博客-CSDN博客 TCP 与UDP 区别_互联网业务udp小包传输_日晞的博客-CSDN博客...
零售行业供应链管理核心KPI指标(一) – 能力、速度、效率和成本
有关零售行业供应链管理KPI指标的综合性分享,涉及到供应链能力、速度、效率和成本总共九大指标,是一个大框架,比较核心也比较综合。 衡量消费品零售企业供应链管理效率和水平的核心KPI通常有哪些? 图片来源-派可数据(…...

MySQL面试题二
1、关系型和非关系型数据库的区别? 关系型数据库的优点 容易理解,因为它采用了关系模型来组织数据。 可以保持数据的一致性。 数据更新的开销比较小。 支持复杂查询(带 where 子句的查询) 非关系型数据库(NOSQL&#x…...

码银送书第五期《互联网广告系统:架构、算法与智能化》
广告平台的建设和完善是一项长期工程。例如,谷歌早于2003年通过收购Applied Semantics开展Google AdSense 项目,而直到20年后的今天,谷歌展示广告平台仍在持续创新和提升。广告平台是负有营收责任的复杂在线平台,对其进行任何改动…...

分布式理论
CAP和BASE CAP C一致性(Consistency) 在分布式环境下,一致性是指数据在多个副本之间能否保持一致性的特征。在一致性的需求下,当一个系统在数据一致的状态下执行更新操作后,应该保证系统的数据仍然处于一致性的状态…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...
