概率论与数理统计:第四章:随机变量的数字特征
文章目录
- Ch4. 随机变量的数字特征
- 1. 数学期望E(X)
- (1)数学期望的概念
- (2)数学期望的性质
- (3)求E(X)的三种方法
- 2. 方差D(X)
- (1)方差的定义及公式
- (2)方差的性质
- 3. 协方差Cov(X,Y)
- (1)协方差定义及公式
- (2)协方差性质
- (3)两种思路求解 C o v ( f , g ) Cov(f,g) Cov(f,g)
- 4. 相关系数 ρ X Y ρ_{XY} ρXY
- (1)ρ的公式
- (2)ρ的性质
- 5.独立性与不相关性
- (1)含义
- (2)判定
- (3)独立性的应用
- ①X,Y独立,则f(X)与g(Y)也独立。
- ②X,Y独立,Cov(X,Y)=0
- 6.切比雪夫不等式
- 7.常见分布的数值特征
- 8.确定未知数的值
Ch4. 随机变量的数字特征
一维随机变量的数字特征:数学期望、方差
二维随机变量的数字特征:协方差、相关系数
1. 数学期望E(X)
(1)数学期望的概念
数学期望,又称均值
1.离散型
①一维离散型随机变量X的数学期望: E X EX EX
E X = ∑ i = 1 ∞ x i p i EX=\sum\limits_{i=1}^∞x_ip_i EX=i=1∑∞xipi
②一维离散型随机变量的函数的期望: E [ g ( X ) ] E[g(X)] E[g(X)]
E [ g ( X ) ] = ∑ i = 1 ∞ g ( x i ) p i E[g(X)]=\sum\limits_{i=1}^∞g(x_i)p_i E[g(X)]=i=1∑∞g(xi)pi
E ( X 2 ) = ∑ i = 1 ∞ x i 2 p i E(X^2)=\sum\limits_{i=1}^∞x_i^2p_i E(X2)=i=1∑∞xi2pi

③二维离散型随机变量的函数的期望: E [ g ( X , Y ) ] E[g(X,Y)] E[g(X,Y)]


例题1:16年08. 求E(XY)

分析:
| X | 0 | 1 | 2 |
|---|---|---|---|
| p p p | 4 9 \dfrac{4}{9} 94 | 4 9 \dfrac{4}{9} 94 | 1 9 \dfrac{1}{9} 91 |
| Y | 0 | 1 | 2 |
|---|---|---|---|
| p p p | 4 9 \dfrac{4}{9} 94 | 4 9 \dfrac{4}{9} 94 | 1 9 \dfrac{1}{9} 91 |
E ( X ) = 1 × 4 9 + 2 × 1 9 = 2 3 = E ( Y ) \rm E(X)=1×\dfrac{4}{9}+2×\dfrac{1}{9}=\dfrac{2}{3}=E(Y) E(X)=1×94+2×91=32=E(Y)
E ( X 2 ) = 4 9 + 2 2 × 1 9 = 8 9 = E ( Y 2 ) \rm E(X^2)=\dfrac{4}{9}+2^2×\dfrac{1}{9}=\dfrac{8}{9}=E(Y^2) E(X2)=94+22×91=98=E(Y2)
D ( X ) = E ( X 2 ) − E 2 ( X ) = 8 9 − 4 9 = 4 9 = D ( Y ) \rm D(X)=E(X^2)-E^2(X)=\dfrac{8}{9}-\dfrac{4}{9}=\dfrac{4}{9}=D(Y) D(X)=E(X2)−E2(X)=98−94=94=D(Y)
难点、易错点在求E(XY)
P{XY=4}=P{X=2,Y=2}=0
P{XY=2}=P{X=2,Y=1}+P{X=1,Y=2}=0
P{XY=1}=P{X=1,Y=1}= 2 × 1 3 × 1 3 = 2 9 2×\dfrac{1}{3}×\dfrac{1}{3}=\dfrac{2}{9} 2×31×31=92
P{XY=0}= 1 − 2 9 = 7 9 1-\dfrac{2}{9}=\dfrac{7}{9} 1−92=97
| XY | 0 | 1 | 2 | 4 |
|---|---|---|---|---|
| p p p | 7 9 \dfrac{7}{9} 97 | 2 9 \dfrac{2}{9} 92 | 0 | 0 |
∴ E ( X Y ) = 2 9 E(XY)=\dfrac{2}{9} E(XY)=92
ρ X Y = C o v ( X Y ) D ( X ) D ( Y ) = E ( X Y ) − E ( X ) ⋅ E ( Y ) D ( X ) ⋅ D ( Y ) = 2 9 − 4 9 4 9 = − 1 2 \rm ρ_{XY}=\dfrac{Cov(XY)}{\sqrt{D(X)D(Y)}}=\dfrac{E(XY)-E(X)·E(Y)}{\sqrt{D(X)·D(Y)}}=\dfrac{\dfrac{2}{9}-\dfrac{4}{9}}{\dfrac{4}{9}}=-\dfrac{1}{2} ρXY=D(X)D(Y)Cov(XY)=D(X)⋅D(Y)E(XY)−E(X)⋅E(Y)=9492−94=−21
答案:A
2.连续型
①一维连续型随机变量X的数学期望: E X EX EX
E ( X ) = ∫ − ∞ + ∞ x f ( x ) d x E(X)=\int_{-∞}^{+∞}xf(x)dx E(X)=∫−∞+∞xf(x)dx
②一维连续型随机变量的函数的数学期望: E [ g ( X ) ] E[g(X)] E[g(X)]
E ( Y ) = E [ g ( X ) ] = ∫ − ∞ + ∞ g ( x ) f ( x ) d x E(Y)=E[g(X)]=\int_{-∞}^{+∞}g(x)f(x)\rm dx E(Y)=E[g(X)]=∫−∞+∞g(x)f(x)dx
注:
① E ( X 2 ) = ∫ − ∞ + ∞ x 2 f ( x ) d x E(X^2)=\int_{-∞}^{+∞}x^2f(x)dx E(X2)=∫−∞+∞x2f(x)dx
②若概率密度函数 f ( x ) f(x) f(x)为偶函数,则 E ( 奇函数 ) = 0 E(奇函数)=0 E(奇函数)=0。
例如X~N(0,1),φ(x)为偶函数,则E(X的奇函数)如E(X³)=0。

③二维连续型随机变量的函数的数学期望: E [ g ( X , Y ) ] E[g(X,Y)] E[g(X,Y)]
(X,Y)为连续型随机变量,概率密度为f(x,y),且 ∫ − ∞ + ∞ g ( x , y ) f ( x , y ) d x d y \int_{-∞}^{+∞}g(x,y)f(x,y)dxdy ∫−∞+∞g(x,y)f(x,y)dxdy绝对收敛,
则(X,Y)的数学期望为: E [ g ( X , Y ) ] = ∫ − ∞ + ∞ g ( x , y ) f ( x , y ) d x d y E[g(X,Y)]=\int_{-∞}^{+∞}g(x,y)f(x,y)dxdy E[g(X,Y)]=∫−∞+∞g(x,y)f(x,y)dxdy
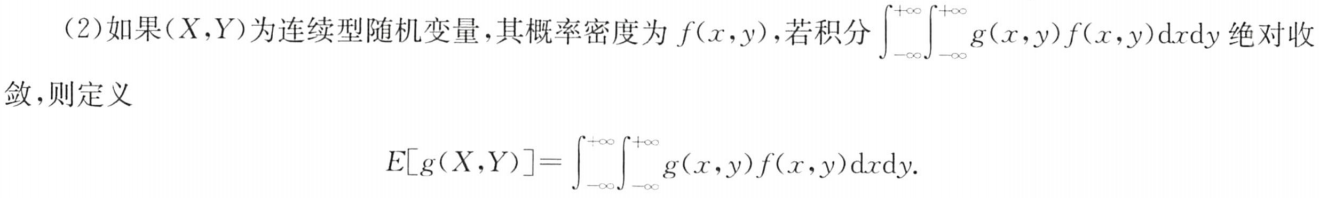
(2)数学期望的性质
1.线性性质:
① E C = C EC=C EC=C
② E ( a X + C ) = a E X + C E(aX+C)=aEX+C E(aX+C)=aEX+C
③ E ( X ± Y ) = E X ± E Y E(X±Y)=EX±EY E(X±Y)=EX±EY
2.若X,Y独立,则:
① E ( X Y ) = E X ⋅ E Y E(XY)=EX·EY E(XY)=EX⋅EY
② E [ f ( X ) g ( Y ) ] = E [ f ( X ) ] ⋅ E [ g ( Y ) ] E[f(X)g(Y)]=E[f(X)]·E[g(Y)] E[f(X)g(Y)]=E[f(X)]⋅E[g(Y)]
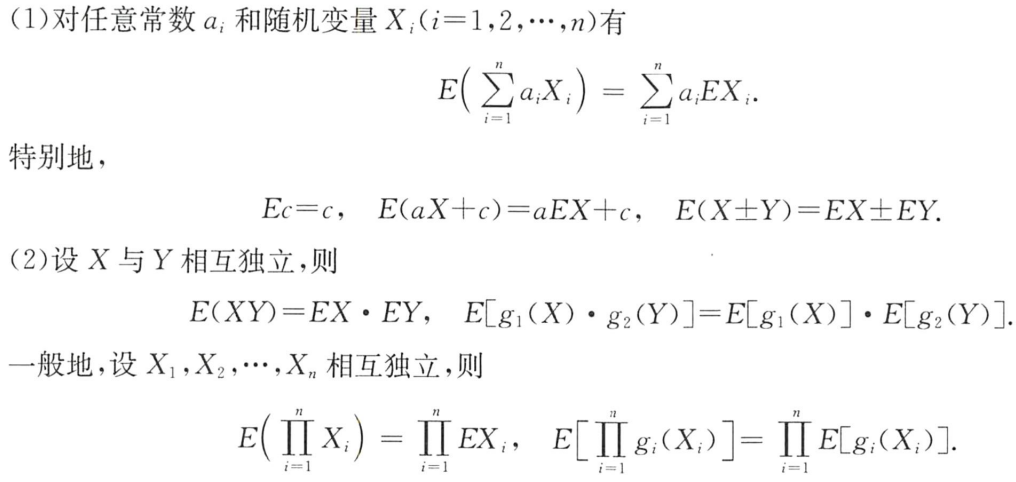
例题1:20年14.

分析:只要随机变量相同,其函数的概率密度仍不变。求E(XsinX)时的概率密度仍为f(x)
E ( X ) = ∫ − ∞ + ∞ x f ( x ) d x E(X)=\int_{-∞}^{+∞}xf(x)dx E(X)=∫−∞+∞xf(x)dx
E [ g ( X ) ] = ∫ − ∞ + ∞ g ( x ) f ( x ) d x E[g(X)]=\int_{-∞}^{+∞}g(x)f(x)\rm dx E[g(X)]=∫−∞+∞g(x)f(x)dx
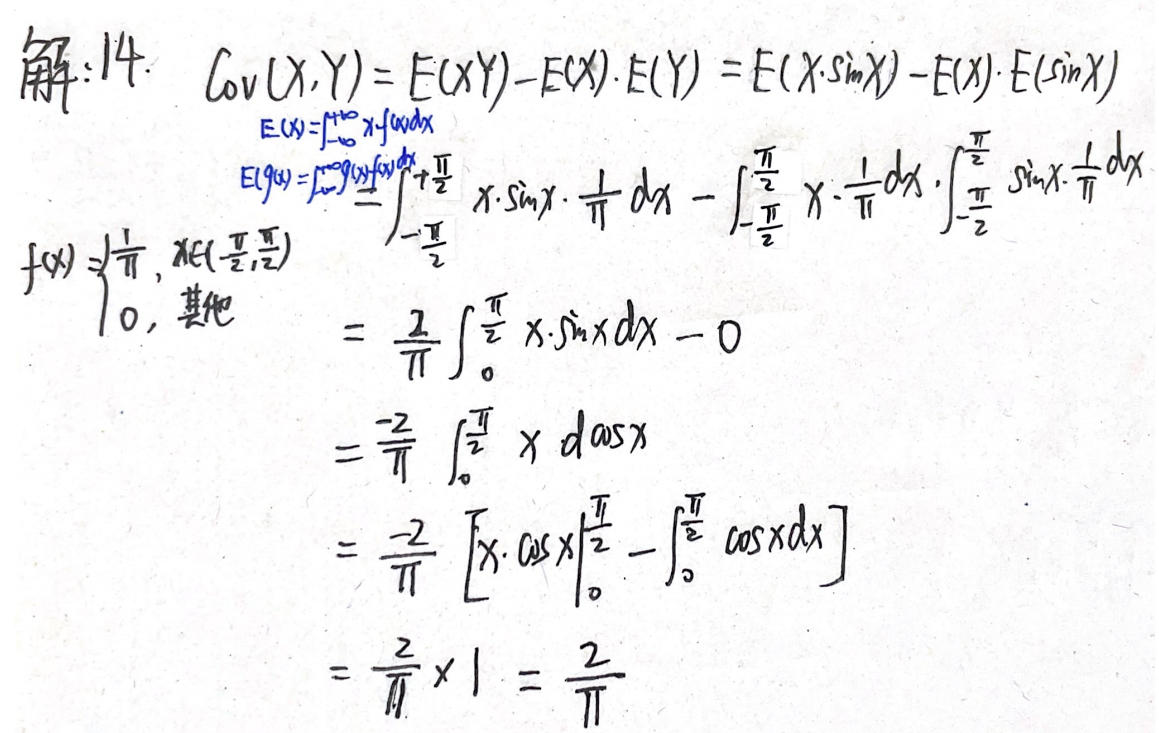
答案: 2 π \dfrac{2}{π} π2
例题2:18年23(2)
(3)求E(X)的三种方法
1.先用数学期望的性质,化简目标数学期望:
如 E ( X + Y ) = E X + E Y E(X+Y)=EX+EY E(X+Y)=EX+EY
2.特殊分布的数字特征:
X是否满足某一特殊分布,若满足,根据其数字特征直接得出EX
3.定义法:
若上述两项都不能再使用后,别无选择只能用定义。如连续型随机变量的数学期望为 E ( X ) = ∫ − ∞ + ∞ x f ( x ) d x E(X)=\int_{-∞}^{+∞}xf(x)dx E(X)=∫−∞+∞xf(x)dx
(1)定义法求解 E ( X ) = ∫ − ∞ + ∞ x f ( x ) d x E(X)=\int_{-∞}^{+∞}xf(x)dx E(X)=∫−∞+∞xf(x)dx时,若 x f ( x ) xf(x) xf(x)为偶函数,则可化为两倍正区间的积分 E ( X ) = 2 ∫ 0 + ∞ x f ( x ) d x E(X)=2\int_0^{+∞}xf(x)dx E(X)=2∫0+∞xf(x)dx
(2)伽马函数: ∫ 0 + ∞ x n ⋅ e − x d x = n ! \int_0^{+∞}x^n·e^{-x}dx=n! ∫0+∞xn⋅e−xdx=n!
例题1:24基础30讲 4.9

分析:
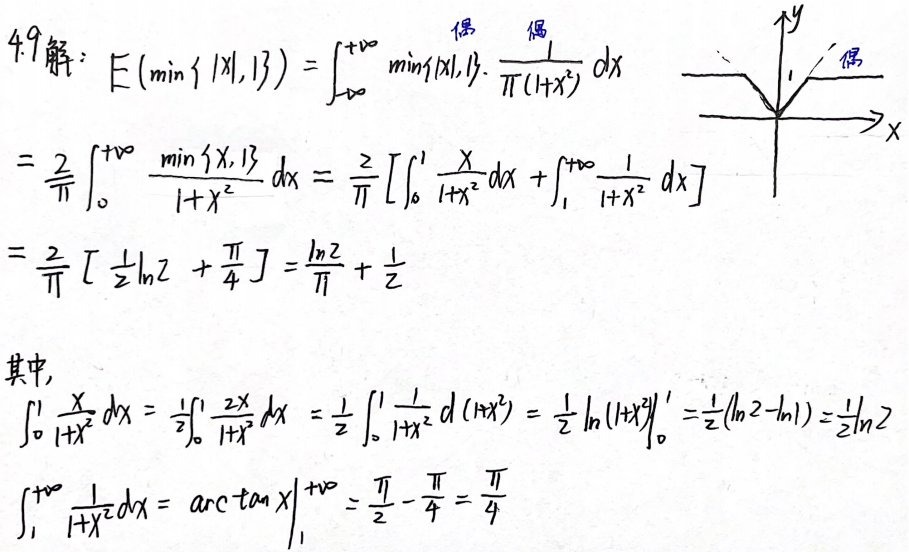
答案:
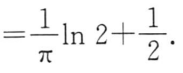
2. 方差D(X)
(1)方差的定义及公式
D ( X ) = E [ ( X − E X ) 2 ] = E ( X 2 ) − E 2 ( X ) D(X)=E[(X-EX)^2]=E(X^2)- E^2(X) D(X)=E[(X−EX)2]=E(X2)−E2(X)
E ( X 2 ) = D ( X ) + E 2 ( X ) E(X²)=D(X)+E²(X) E(X2)=D(X)+E2(X)

(2)方差的性质
① D C = 0 DC=0 DC=0
② D ( C X ) = C 2 D X D(CX)=C²DX D(CX)=C2DX
③ D ( a X + C ) = a 2 D X D(aX+C)=a^2DX D(aX+C)=a2DX
④ D ( X ± Y ) = D X + D Y ± 2 C o v ( X , Y ) D(X±Y)=DX+DY±2{\rm Cov}(X,Y) D(X±Y)=DX+DY±2Cov(X,Y)
⑤ D ( a X ± b Y ) = a 2 D X + b 2 D Y ± 2 a b C o v ( X , Y ) D(aX±bY)=a²DX+b²DY±2ab{\rm Cov}(X,Y) D(aX±bY)=a2DX+b2DY±2abCov(X,Y) 若X与Y独立,则Cov(X,Y)=0
⑥ C o v ( X , X ) = D ( X ) {\rm Cov}(X,X)=D(X) Cov(X,X)=D(X)
补充⑦:当X,Y独立时, D ( X Y ) = D X ⋅ D Y + ( E X ) 2 D Y + ( E Y ) 2 D X D(XY)=DX·DY+(EX)²DY+(EY)²DX D(XY)=DX⋅DY+(EX)2DY+(EY)2DX
补充⑧:当 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn相互独立且有相同的方差 σ 2 σ^2 σ2时,记 X ‾ = 1 n ∑ i = 1 n X i \overline{X}=\dfrac{1}{n}\sum\limits_{i=1}^nX_i X=n1i=1∑nXi,则 D ( X i − X ‾ ) = n − 1 n σ 2 D(X_i-\overline{X})=\dfrac{n-1}{n}σ^2 D(Xi−X)=nn−1σ2

例题1:22年8. 方差的性质
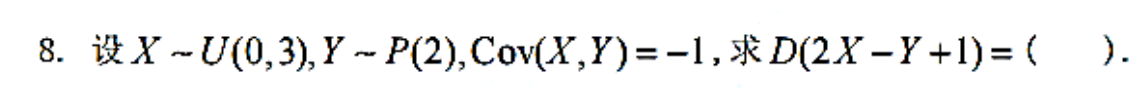
分析:注意,X与Y没说独立就是不独立,不要误选了5
X~U(0,3),D(X)= ( 3 − 0 ) 2 12 = 3 4 \frac{(3-0)²}{12}=\frac{3}{4} 12(3−0)2=43
Y~P(2),D(Y)=2
D(2X-Y+1)=D(2X-Y)=4D(X)+D(Y)-4Cov(X,Y)= 4 × 3 4 + 2 − 4 × ( − 1 ) 4×\frac{3}{4}+2-4×(-1) 4×43+2−4×(−1)=3+2+4=9
答案:9
例题2:11年14. E ( X 2 ) = D ( X ) + E 2 ( X ) \rm E(X²)=D(X)+E²(X) E(X2)=D(X)+E2(X)
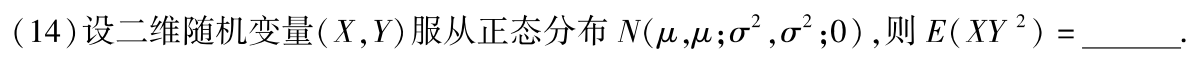
分析:
∵ρ=0,∴X与Y不相关 又∵(X,Y)服从正态分布,∴X与Y独立
E ( X Y 2 ) = X 与 Y 独立 E ( X ) ⋅ E ( Y 2 ) = E ( X ) ⋅ [ D ( Y ) + E 2 ( Y ) ] = μ ( σ 2 + μ 2 ) \rm E(XY²)\xlongequal[]{X与Y独立}E(X)·E(Y²)=E(X)·[D(Y)+E²(Y)]=μ(σ²+μ²) E(XY2)X与Y独立E(X)⋅E(Y2)=E(X)⋅[D(Y)+E2(Y)]=μ(σ2+μ2)
答案:μ(σ²+μ²)
例题3:18年23(2)
3. 协方差Cov(X,Y)
(1)协方差定义及公式
C o v ( X , Y ) = E [ ( X − E X ) ( Y − E Y ) ] = E ( X Y ) − E ( X ) ⋅ E ( Y ) {\rm Cov}(X,Y) =E[(X-EX)(Y-EY)]={\rm E}(XY)-{\rm E}(X)·{\rm E}(Y) Cov(X,Y)=E[(X−EX)(Y−EY)]=E(XY)−E(X)⋅E(Y)
计算Cov(X,Y)=EXY-EX·EY时,简化计算:
①若有EX=0则EY不用算了,若有EY=0则EX不用算了。
②若E(XY)用定义发现是奇函数,则在对称区间上积分为0
(2)协方差性质
① C o v ( X , C ) = 0 {\rm Cov}(X,C)=0 Cov(X,C)=0
② C o v ( X , Y ) = C o v ( Y , X ) {\rm Cov}(X,Y)={\rm Cov}(Y,X) Cov(X,Y)=Cov(Y,X) 【 ρ X Y = ρ Y X ρ_{XY}=ρ_{YX} ρXY=ρYX】
③ C o v ( X , X ) = D ( X ) {\rm Cov}(X,X) ={\rm D}(X) Cov(X,X)=D(X) 【 ρ X X = 1 ρ_{XX}=1 ρXX=1】
④ C o v ( X 1 + X 2 , Y ) = C o v ( X 1 , Y ) + C o v ( X 2 , Y ) {\rm Cov}(X₁+X₂,Y) ={\rm Cov}(X₁,Y) +{\rm Cov}(X₂,Y) Cov(X1+X2,Y)=Cov(X1,Y)+Cov(X2,Y)
⑤ C o v ( a X + c , b Y + d ) = a b C o v ( X , Y ) {\rm Cov}(aX+c,bY+d) =ab\ {\rm Cov}(X,Y) Cov(aX+c,bY+d)=ab Cov(X,Y) 【Cov中,有常数可以直接抹去,系数可以直接提出来】
⑥若X与Y独立,则Cov(X,Y)=0 (独立是充分不必要条件,不相关是充要条件)
1.②证明: C o v ( X , X ) = E ( X ⋅ X ) − E X ⋅ E X = E ( X 2 ) − E 2 ( X ) = D ( X ) {\rm Cov}(X,X) = E(X·X)-EX·EX=E(X^2)-E^2(X)={\rm D}(X) Cov(X,X)=E(X⋅X)−EX⋅EX=E(X2)−E2(X)=D(X)
2.性质应用举例: C o v ( X , − X + n ) = C o v ( X , − X ) + C o v ( X , n ) = − C o v ( X , X ) + 0 = − D ( x ) {\rm Cov}(X,-X+n)={\rm Cov}(X,-X)+{\rm Cov}(X,n)=-{\rm Cov}(X,X)+0=-D(x) Cov(X,−X+n)=Cov(X,−X)+Cov(X,n)=−Cov(X,X)+0=−D(x)
例题1:23李林六套卷(一) 9.

分析:用协方差的性质求Cov
求Cov
①协方差的定义(公式):Cov(XY)=E(XY)-E(X)E(Y)
②协方差的性质

答案:A
例题2:01年10.

分析: X + Y = n , ∴ Y = − X + n X+Y=n,∴Y=-X+n X+Y=n,∴Y=−X+n
① ρ X Y = C o v ( X , Y ) D ( X ) D ( Y ) = C o v ( X , − X + n ) D ( X ) D ( − X + n ) = − D ( X ) D ( X ) ρ_{XY}=\dfrac{Cov(X,Y)}{\sqrt{D(X)D(Y)}}=\dfrac{Cov(X,-X+n)}{\sqrt{D(X)D(-X+n)}}=\dfrac{-D(X)}{D(X)} ρXY=D(X)D(Y)Cov(X,Y)=D(X)D(−X+n)Cov(X,−X+n)=D(X)−D(X)
② P { Y = − X + n } = 1 , a = − 1 < 0 P\{Y=-X+n\}=1,a=-1<0 P{Y=−X+n}=1,a=−1<0,∴负相关, ρ X Y = − 1 ρ_{XY}=-1 ρXY=−1
答案:A
(3)两种思路求解 C o v ( f , g ) Cov(f,g) Cov(f,g)
1.先用Cov的性质: f = 3 X + Y 2 , g = X − 2 Y 3 f=\dfrac{3X+Y}{2},g=\dfrac{X-2Y}{3} f=23X+Y,g=3X−2Y
2.先用Cov的定义,先不要代入fg:
4. 相关系数 ρ X Y ρ_{XY} ρXY
(1)ρ的公式
ρ = C o v ( X , Y ) D X D Y ρ=\dfrac{Cov(X,Y)}{\sqrt{DX}\sqrt{DY}} ρ=DXDYCov(X,Y)称为随机变量X与Y的相关系数。
ρ X Y ρ_{XY} ρXY是否为正负零,只需要看 C o v ( X , Y ) Cov(X,Y) Cov(X,Y)是否为正负零
(2)ρ的性质
1.对称性:
① ρ X Y = ρ Y X ρ_{XY}=ρ_{YX} ρXY=ρYX
② ρ X X = 1 ρ_{XX}=1 ρXX=1
2.有界性:
− 1 ≤ ρ X Y ≤ 1 -1≤ρ_{XY}≤1 −1≤ρXY≤1
3.正相关、负相关、不相关
P { Y = a X + b } = 1 ⇔ ∣ ρ X Y = 1 ∣ { a > 0 , ρ = 1 ( 正相关 ) a < 0 , ρ = − 1 ( 负相关 ) P\{Y=aX+b\}=1\Leftrightarrow |ρ_{XY}=1|\left\{\begin{aligned} a>0&,ρ=1 &(正相关)\\ a<0&,ρ=-1 &(负相关) \end{aligned}\right. P{Y=aX+b}=1⇔∣ρXY=1∣{a>0a<0,ρ=1,ρ=−1(正相关)(负相关)
P { Y = a X + b } = 0 ⇔ ρ X Y = 0 ( 不相关 ) P\{Y=aX+b\}=0\Leftrightarrow ρ_{XY}=0 \quad(不相关) P{Y=aX+b}=0⇔ρXY=0(不相关)
ρ X Y = 0 ρ_{XY}=0 ρXY=0称为X与Y不相关,即 无线性相关性。
ρ X Y ≠ 0 ρ_{XY}≠0 ρXY=0则称为X与Y相关。即 有线性相依性。
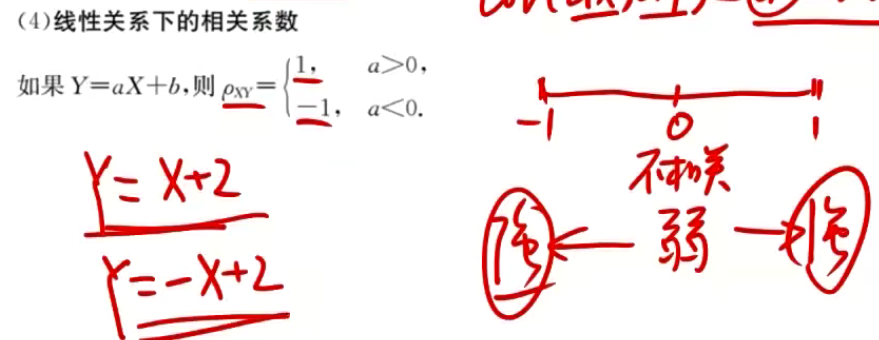
例题1:16年8.

答案:A
例题2:01年10.
5.独立性与不相关性
(1)含义
| 独立/相关 | 含义 |
|---|---|
| 不独立 | 有任意函数关系 |
| 独立 | 无任何函数关系 |
| 相关 | 有线性函数关系 |
| 不相关 | ρXY= 0,X与Y无线性函数关系,但有可能有其他非线性函数关系 |
①独立,一定不相关:没有任何函数关系,自然也没有线性函数关系
②相关,一定不独立:有线性函数关系,算是X与Y有一种函数关系了,不独立。
③不相关,不一定独立:没有线性函数关系,但可能有非线性函数关系
注:仅当(X,Y)服从二维正态分布时,独立与不相关是等价的。其他时候,独立是不相关的充分条件。
(2)判定
1.相关性:用数字特征判定相关性 (5个不相关的等价条件)
\quad ①X与Y不相关
⇔ \Leftrightarrow ⇔ ② ρ X Y = 0 ρ_{XY}=0 ρXY=0
⇔ \Leftrightarrow ⇔ ③ C o v ( X , Y ) = 0 Cov(X,Y)=0 Cov(X,Y)=0
⇔ \Leftrightarrow ⇔ ④ E ( X Y ) = E X ⋅ E Y E(XY)=EX·EY E(XY)=EX⋅EY
⇔ \Leftrightarrow ⇔ ⑤ D ( X ± Y ) = D X + D Y D(X±Y)=DX+DY D(X±Y)=DX+DY
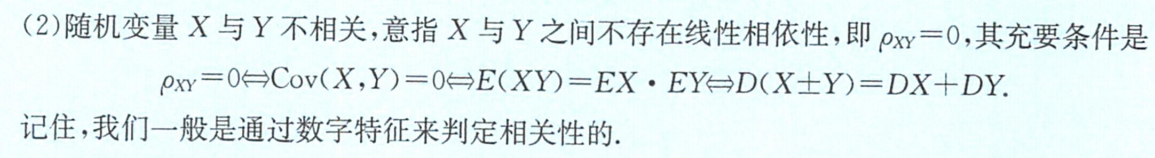
2.独立性:用分布判断独立性,构造事件
\quad ①X与Y不独立
⇔ \Leftrightarrow ⇔ ② P { X ≤ a , Y ≤ a } ≠ P { X ≤ a } ⋅ P { Y ≤ a } P\{X≤a,Y≤a\}≠P\{X≤a\}·P\{Y≤a\} P{X≤a,Y≤a}=P{X≤a}⋅P{Y≤a}
⇔ \Leftrightarrow ⇔ ③ ョ x 0 , y 0 ョx_0,y_0 ョx0,y0使得 F ( x 0 , y 0 ) ≠ F X ( x 0 ) ⋅ F Y ( y 0 ) F(x_0,y_0)≠F_X(x_0)·F_Y(y_0) F(x0,y0)=FX(x0)⋅FY(y0)
联合分布≠边缘分布的乘积

3.判断顺序:
先判断相关性(Cov(x,y)),再判断独立性(看分布)

相关性与独立性的关系,详解见此篇
(3)独立性的应用
①X,Y独立,则f(X)与g(Y)也独立。
如:X,Y独立,则X²与Y²也独立,E(X²Y²)=E(X²)E(Y²)
②X,Y独立,Cov(X,Y)=0
X i X_i Xi独立同分布,则 C o v ( X i , X j ) = 0 ( i ≠ j ) Cov(X_i,X_j)=0 \quad (i≠j) Cov(Xi,Xj)=0(i=j)
6.切比雪夫不等式
①距离均值偏差较大的概率是很小的: P { ∣ X − E ( X ) ∣ ≥ ε } ≤ D ( X ) ε 2 P\{|X-E(X)|≥ε\}≤\dfrac{D(X)}{ε^2} P{∣X−E(X)∣≥ε}≤ε2D(X)
②距离均值偏差较小的概率是比较大的: P { ∣ X − E ( X ) ∣ < ε } ≥ 1 − D ( X ) ε 2 P\{|X-E(X)|<ε\}≥1-\dfrac{D(X)}{ε^2} P{∣X−E(X)∣<ε}≥1−ε2D(X)
①切比雪夫不等式描述的是随机变量X偏离均值一定范围的概率,给的是一个保守的概率。
例如:正态分布 X~N(μ,σ²), P { ∣ X − μ ∣ < 2 σ } ≥ 1 − σ 2 4 σ 2 = 75 % P\{|X-μ|<2σ\}≥1-\dfrac{σ^2}{4σ^2}=75\% P{∣X−μ∣<2σ}≥1−4σ2σ2=75%,而实际上2σ区间内的概率应为95%
②切比雪夫不等式需要求三个值:E(X)、D(X)、ε。由 ∣ X − E ( X ) ∣ |X-E(X)| ∣X−E(X)∣得出ε大小
例题1:01年5. 切比雪夫不等式

分析:
由切比雪夫不等式, P { ∣ X − E ( X ) ∣ ≥ ε } ≤ D ( X ) ε 2 P\{|X-E(X)|≥ε\}≤\dfrac{D(X)}{ε²} P{∣X−E(X)∣≥ε}≤ε2D(X),得此题 ε = 2 , D ( X ) = 2 ε=2,D(X)=2 ε=2,D(X)=2
代入得 P { ∣ X − E ( X ) ∣ ≥ 2 } ≤ 2 2 2 = 1 2 P\{|X-E(X)|≥2\}≤\dfrac{2}{2²}=\dfrac{1}{2} P{∣X−E(X)∣≥2}≤222=21
答案: 1 2 \dfrac{1}{2} 21
例题2:24基础30讲 4.15

分析:
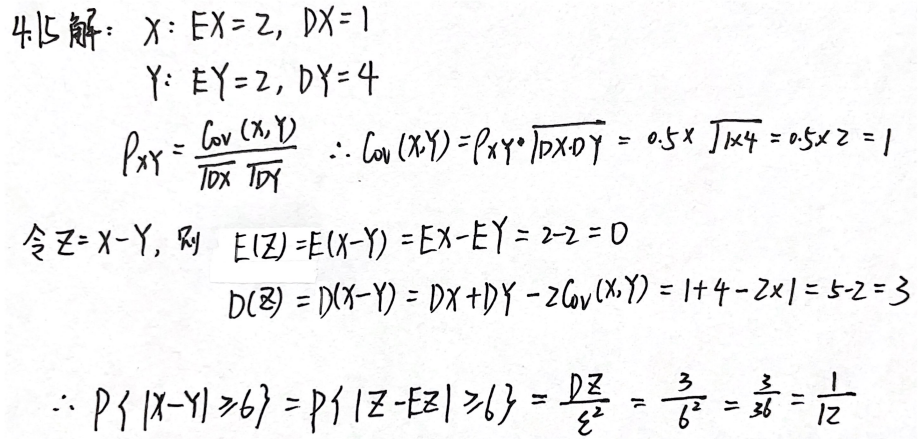
答案: 1 12 \dfrac{1}{12} 121
习题2:23李林六套卷(五)16.
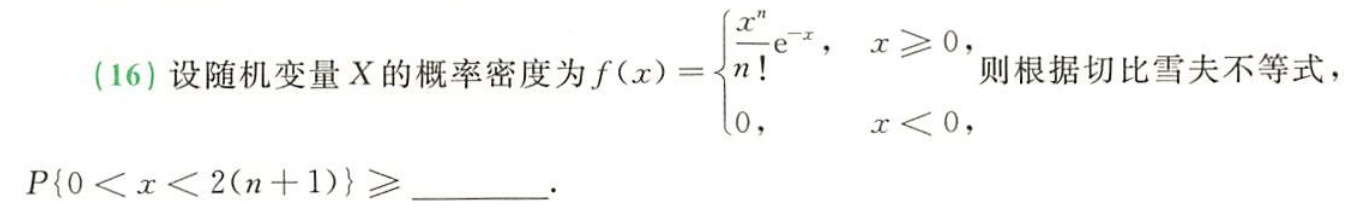
分析:切比雪夫不等式需要求三个值:E(X)、D(X)、ε
由 ∣ X − E ( X ) ∣ |X-E(X)| ∣X−E(X)∣得出ε大小。

答案: n n + 1 \dfrac{n}{n+1} n+1n
7.常见分布的数值特征
| 分布 | 分布律或概率密度 | 数学期望E(X) | 方差D(X) |
|---|---|---|---|
| 0-1分布 | P { X = k } = p k ( 1 − p ) 1 − k , k = 0 , 1 P\{X=k\}=p^k(1-p)^{1-k},k=0,1 P{X=k}=pk(1−p)1−k,k=0,1 | p p p | p ( 1 − p ) p(1-p) p(1−p) |
| 二项分布 B ( n , p ) B(n,p) B(n,p) | P { X = k } = C n k p k ( 1 − p ) n − k P\{X=k\}={\rm C}_n^kp^k(1-p)^{n-k} P{X=k}=Cnkpk(1−p)n−k, k = 0 , 1 , 2 , . . . , n k=0,1,2,...,n k=0,1,2,...,n | n p np np | n p ( 1 − p ) np(1-p) np(1−p) |
| 泊松分布 P ( λ ) P(λ) P(λ) | P { X = k } = λ k k ! e − λ P\{X=k\} = \dfrac{λ^k}{k!}e^{-λ} P{X=k}=k!λke−λ, k = 0 , 1 , 2 , . . . k=0,1,2,... k=0,1,2,... | λ λ λ | λ λ λ |
| 几何分布 G ( p ) G(p) G(p) | P { X = k } = ( 1 − p ) k − 1 p P\{X=k\}=(1-p)^{k-1}p P{X=k}=(1−p)k−1p, k = 1 , 2 , . . . k=1,2,... k=1,2,... | 1 p \dfrac{1}{p} p1 | 1 − p p 2 \dfrac{1-p}{p^2} p21−p |
| 均匀分布 U ( a , b ) U(a,b) U(a,b) | f ( x ) = { 1 b − a , a < x < b 0 ,其他 f(x)=\begin{cases} \dfrac{1}{b-a},a<x<b\\ 0\qquad,其他 \end{cases} f(x)=⎩ ⎨ ⎧b−a1,a<x<b0,其他 | a + b 2 \dfrac{a+b}{2} 2a+b | ( b − a ) 2 12 \dfrac{(b-a)^2}{12} 12(b−a)2 |
| 指数分布 E ( λ ) E(λ) E(λ) | f ( x ) = { λ e − λ x , x > 0 0 , x ≤ 0 f(x)=\begin{cases} λe^{-λx},x>0\\ 0\qquad,x≤0 \end{cases} f(x)={λe−λx,x>00,x≤0 | 1 λ \dfrac{1}{λ} λ1 | 1 λ 2 \dfrac{1}{λ^2} λ21 |
| 正态分布 N ( μ , σ 2 ) N(μ,σ^2) N(μ,σ2) | f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 ( − ∞ < x < + ∞ ) f(x)=\dfrac{1}{\sqrt{2π}σ}e^{-\frac{{(x-μ^)}^2}{2σ^2}} \quad(-∞<x<+∞) f(x)=2πσ1e−2σ2(x−μ)2(−∞<x<+∞) | μ μ μ | σ 2 σ^2 σ2 |
| 卡方分布 χ 2 χ^2 χ2 | E ( χ 2 ) = n E(χ^2)=n E(χ2)=n | D ( χ 2 ) = 2 n D(χ^2)=2n D(χ2)=2n |
例题1:24基础30讲 4.8

分析:
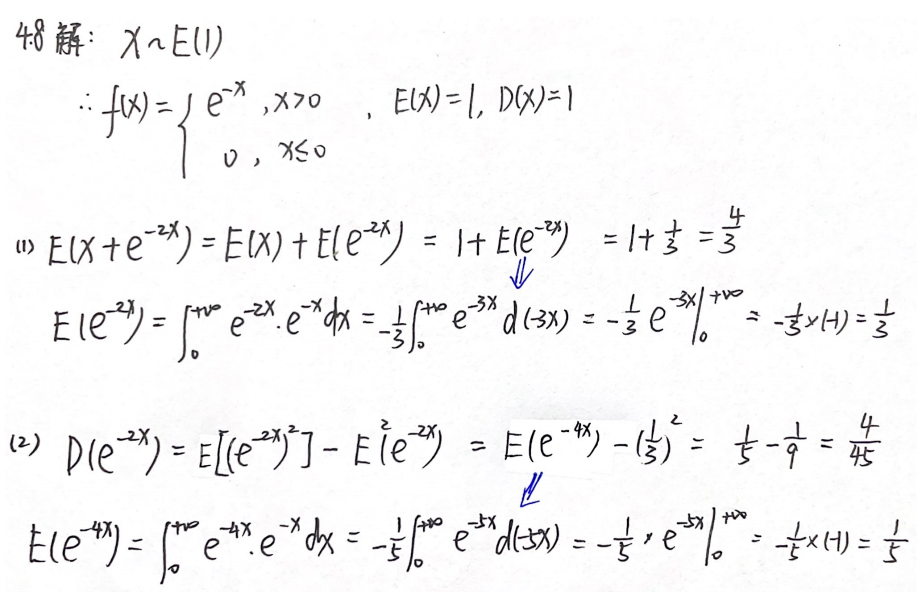
答案: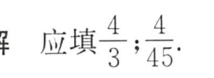
例题2:11年23.(2) 卡方分布

分析:估计量服从卡方分布,用卡方分布的数字特征来求估计量的期望与方差
8.确定未知数的值
1.概率密度的归一性: ∫ − ∞ + ∞ f ( x ) d x = 1 \int_{-∞}^{+∞}f(x)dx=1 ∫−∞+∞f(x)dx=1
2.对比特殊分布
相关文章:

概率论与数理统计:第四章:随机变量的数字特征
文章目录 Ch4. 随机变量的数字特征1. 数学期望E(X)(1)数学期望的概念1.离散型①一维离散型随机变量X的数学期望: E X EX EX②一维离散型随机变量的函数的期望: E [ g ( X ) ] E[g(X)] E[g(X)]③二维离散型随机变量的函数的期望: E [ g ( X , …...

解决饿了么ui的对话框缩放和移动
import Vue from "vue";// v-dialogDrag: 弹窗拖拽水平方向伸缩 /** 使用方法* 将以下代码复制到一个js文件中,然后在入口文件main.js中import引入即可;* 给elementUI的dialog上加上 v-dialogDrag 指令就可以实现弹窗的全屏和拉伸了。* 给…...

Linux 中复制文件并保持修改时间等属性
一、遇到的问题 Linux使用cp命令复制文件备份时,发现文件的修改时间变成当前时间了,想要保留备份文件原有的修改时间及其它文件属性。 二、实现 1、cp命令 在 Linux 中,你可以使用 cp 命令来复制文件,并通过 -p 或 --preserve…...

Hugging News #0814: Llama 2 学习资源大汇总
每一周,我们的同事都会向社区的成员们发布一些关于 Hugging Face 相关的更新,包括我们的产品和平台更新、社区活动、学习资源和内容更新、开源库和模型更新等,我们将其称之为「Hugging News」。本期 Hugging News 有哪些有趣的消息࿰…...
-阶梯线图(Step Chart))
可视化绘图技巧100篇进阶篇(五)-阶梯线图(Step Chart)
目录 前言 图表类型特征 适用场景 图例 绘图工具及代码实现 ECharts SMARTBI...

GPT带我学-设计模式-命令模式
1 你知道设计模式的命令模式吗 是的,我知道设计模式中的命令模式。命令模式是一种行为型设计模式,它将请求封装成一个对象,从而允许使用不同的请求、队列或日志来参数化其他对象。命令模式还支持撤销操作,并且可以提供事务的实现…...

互联网发展历程:跨越远方,路由器的启示
互联网的蓬勃发展,一直在追求更广阔的连接,更遥远的距离。然而,在早期的网络中,人们面临着连接距离有限的问题。一项重要的技术应运而生,那就是“路由器”。 连接受限的问题:距离有限 早期的网络受限于直接…...
postman入门基础 —— 接口测试流程
一、编写接口测试计划 接口测试计划和功能测试计划目标一致,都是为了确认需求、确定测试环境、确定测试方法,为设计测试用例做准备,初步制定接口测试进度方案。一般来说,接口测试计划包括概述、测试资源、测试功能、测试重点、测试…...

springcloud+nacos实现灰度发布
灰度发布 gateway网关实现灰度路由 灰度发布实体 package com.scm.boss.common.bean;import lombok.Data; import lombok.experimental.Accessors;import java.io.Serializable;/*** 灰度发布实体*/ Data Accessors(chain true) public class GrayBean implements Serializ…...

【C++笔记】C++之类与对象(上)
【C笔记】C之类与对象(上) 1、类是结构体的升级2、类中可以定义的东西3、类访问限定符4、类的声明5、类的实例化(定义)6、类的大小的计算7、this指针 1、类是结构体的升级 C的一个显著特征就是兼容C语言,所以C把结构体“升级”成了“类”&am…...

ebay灯串UL报告 UL588检测标准
季节性和装饰性照明用品即灯串以及配件都是便携式插头连接的临时性商品,最大额定输入电压为 120 伏。 由 ILAC ISO 17025 认证的实验室出具的检测报告,确认每件商品均已经过检测,符合下列要求: 季节性和装饰性照明用品(灯串&…...
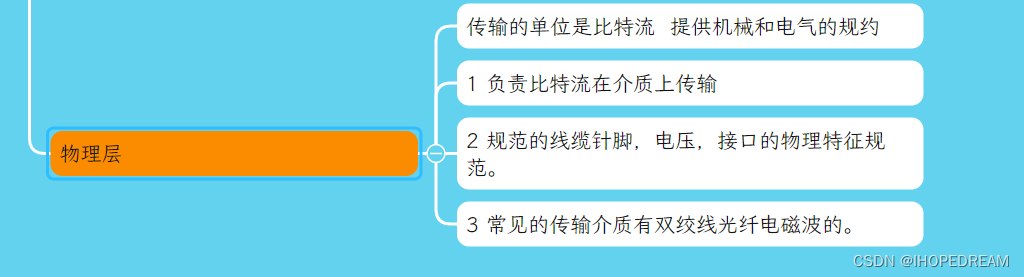
TCP/IP协议追层分析物理层(第三十九课)
TCP/IP协议追层分析物理层(第三十九课) 1 物理层:建立、维护、断开物理连接,定义了接口及介质,实现了比特流的传输。 1、传输介质分类 有线介质:网线(双绞线)、光纤 无线介质:无线电 微波 激光 红外线 2、双绞线分类: 五类cat5: 适用于100Mbps 超五类cat5e:适用于…...
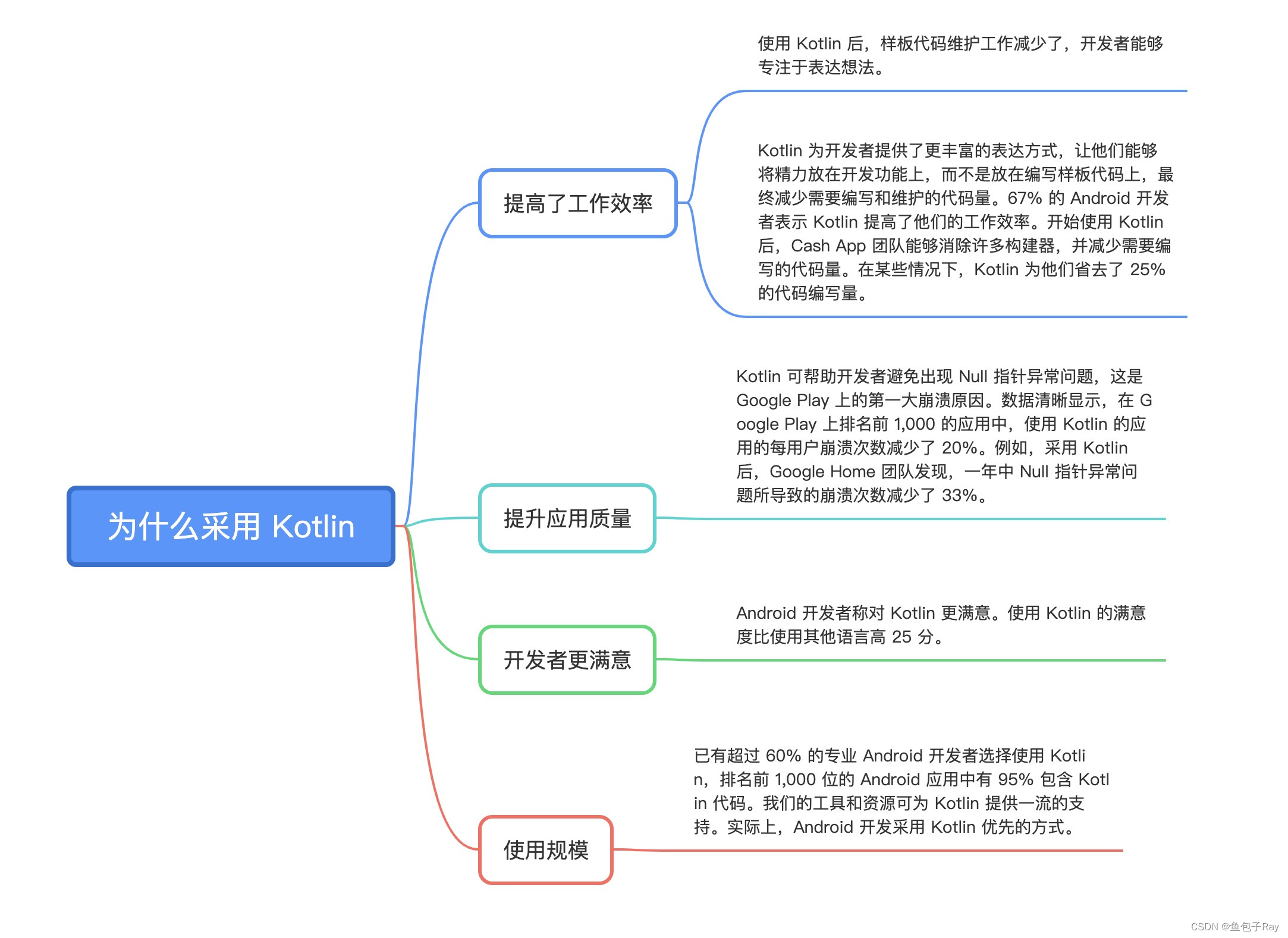
Kotlin优点及为什么使用Kotlin
文章目录 一 Hello Kotlin二 Kotlin优点三 团队为什么采用 Kotlin 一 Hello Kotlin Kotlin和Andriod 二 Kotlin优点 三 团队为什么采用 Kotlin...
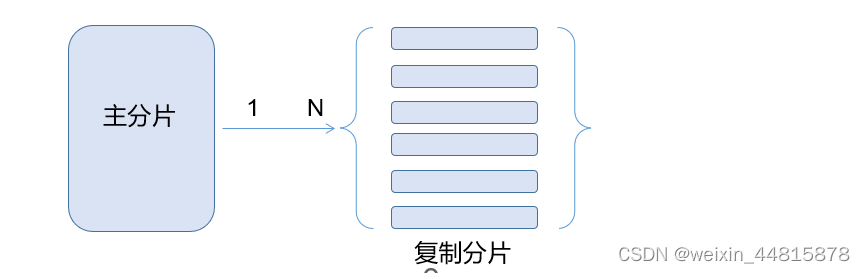
ES 概念
es 概念 Elasticsearch是分布式实时搜索、实时分析、实时存储引擎,简称(ES)成立于2012年,是一家来自荷兰的、开源的大数据搜索、分析服务提供商,为企业提供实时搜索、数据分析服务,支持PB级的大数据。 -- …...
Fairy下载和使用
写在最前:本系列中将会涉及到 Unity,C#,Lua和FairyGUI(FGUI)。 FairyGUI介绍 官网: FairyGUI 编辑器下载: FairyGUI 截至文档记录最新版: https://res.fairygui.com/FairyGUI-Ed…...

隧道HTTP优化程序示例
作为专业爬虫程序员,我们经常需要使用代理服务器处理大量的请求。但是,单一服务器往往无法承担高并发请求和HTTPS加密的压力,这时候我们可以利用CDN来优化性能,并实现反向代理和HTTPS加速。下面,让我们一步步来了解。 …...

Flink源码之State创建流程
StreamOperatorStateHandler 在StreamTask启动初始化时通过StreamTaskStateInitializerImpl::streamOperatorStateContext会为每个StreamOperator 创建keyedStatedBackend和operatorStateBackend,在AbstractStreamOperator中有个StreamOperatorStateHandler成员变量…...
selenium常见等待机制及其特点和使用方法
目录 1、强制等待 2、隐式等待 3、显示等待 1、强制等待 强制等待是在程序中直接调用Thread.sleep(timeout) ,来完成的,该用法的优点是使用起来方便,语法也比较简单,缺点就是需要强制等待固定的时间,可能会造成测试的时间过…...

C++物件数组的常用方法介绍
以下代码建立了一个物件数组Student,并展示了如何计算物件数组的长度,如何从物件数组中找到特定的对象,如何根据数组的不同参数进行排序,以及如何找到最大和最小值。 #include <iostream> #include <algorithm>using…...

云计算:新一代的技术革命
云计算,作为21世纪的一项重要技术革命,已在全球范围内引发了深远的影响。它改变了我们存储和处理数据的方式,使得企业无需再建设和维护昂贵的本地服务器和数据中心。本文将深入探讨云计算的基本概念,类型,主要优点&…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
