2023年国赛数学建模思路 - 复盘:人力资源安排的最优化模型
文章目录
- 0 赛题思路
- 1 描述
- 2 问题概括
- 3 建模过程
- 3.1 边界说明
- 3.2 符号约定
- 3.3 分析
- 3.4 模型建立
- 3.5 模型求解
- 4 模型评价与推广
- 5 实现代码
- 建模资料
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 描述
某大学数学系人力资源安排问题是一个整数规划的最优化问题,通过具体分析数学系现有的技术力量和各方面的约束条件,在问题一的求解中,可以列出一天最大直接收益的整数规划,求得最大的直接收益是42860元;而在问题二的求解中,由于教授一个星期只能工作四天,副教授一个星期只能工作五天,在这样的约束条件下,列出一个星期里最大直接收益的整数规划模型,求得其最大直接收益是198720元。
2 问题概括
数学系的教师资源有限,现有四个项目来源于四个不同的客户,工作的难易程度不一,各项目对有关技术人员的报酬不同。所以:
1.在满足工作要求的情况下,如何分配数学系现有的技术力量,使得其一天的直接收益最大?
2.在教授与副教授工作时间受到约束的条件下,如何分配数学系现有的技术力量,使得其在一个星期里的直接收益最大?
3 建模过程
3.1 边界说明
1.不同技术力量的人每天被安排工作的几率是相等的,且相同职称的个人去什么地方工作是随机的;
2.客户除了支付规定的工资额外,在工作期间里,还要支付所有相关的花费(如餐费,车费等);
3.当天工作当天完成.
3.2 符号约定

3.3 分析
由题意可知各项目对不同职称人员人数都有不同的限制和要求.对客户来说质量保证是关键,而教授相对稀缺,因此各项目对教授的配备有不能少于一定数目的限制.其中由于项目技术要求较高,助教不能参加.而两项目主要工作是在办公室完成,所以每人每天有50元的管理费开支.
由以上分析可得:最大直接收益=总收益-技术人员工资-、两地保管费.
3.4 模型建立



3.5 模型求解
相关数据表格如下:
数学系的职称结构及工资情况
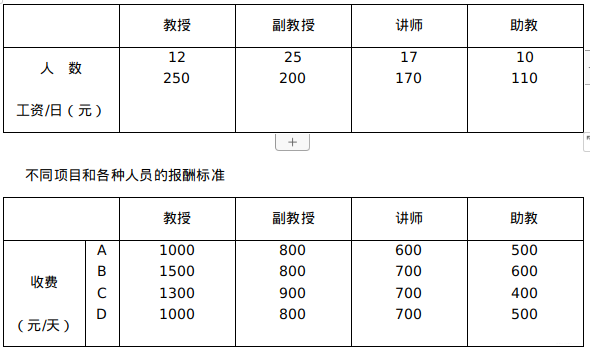
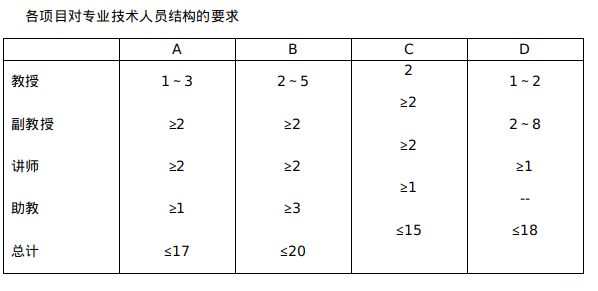
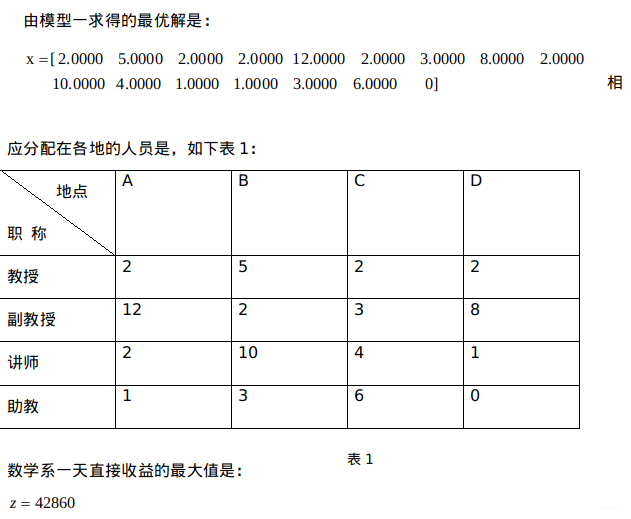
4 模型评价与推广
本模型通过合理的假设,充分考虑各方面的限制条件,得出的人员安排和直接收益
都是本模型的最优解与最优值,对武汉大学数学系的人力资源安排有一定的指导作用。但从模型假设中,我们可以知道对数
学系现有的技术力量的安排是随机的,在相同工作时段里,可能会出现部分人工作次数较多,而部分人较少的不公平情况。
所以在满足工作需求的情况下,分配工作时应该要人为地尽量使得每个人的工作次数不要相差太远,或者相等。
此模型通过对人力资源的调配,从量化的角度得出数学系的最大直接收益。利用此模型的方法可以求出所有类似本模型的线性规划模型。但是,本模型只是单目标的规划,可以在此基础上,增加目标要求。如在数学系的直接收益尽可能大的基础上,使得客户所花费的资金最少,等等。从而建立多目标规划模型。解决更为复杂的实际问题。
5 实现代码
f=[-1000;-800;-550;-450;-1500;-800;-650;-550;-1300;-900;-650;-350;-1000;-800;-650;-450];
A=zeros(9,16);
for i=1:1for j=1:16A(i,j)=1; end
end
for i=2:5for j=i-1:4:11+iA(i,j)=1;end
end
i0=0;
for i=6:9for j=i0+1:(i-5 )*4A(i,j)=1;endi0=j;
end
b=[64;17;20;15;18;12;25;17;10];
Aeq=zeros(1,16);
Aeq(1,3)=1;
beq=[2];
LB=[1;2;2;1;2;2;2;2;2;2;2;1;1;3;1;0];
UB=[3;5;2;2;inf;inf;inf;8;inf;inf;inf;inf;inf;inf;inf;0];
[x,fval]=linprog(f,A,b,Aeq,beq,LB,UB)f=[-1000;-1000;-1000;-1000;-1000;-1000;-1000;-1500;-1500;-1500;-1500;-1500;-1500;-1500;-1250;-1250;-1250;-1250;-1250;-1250;-1250;-950;-950;-950;-950;-950;-950;-950;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-800;-850;-850;-850;-850;-850;-850;-850;-750;-750;-750;-750;-750;-750;-750;-600;-600;-600;-600;-600;-600;-600;-700;-700;-700;-700;-700;-700;-700;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-650;-500;-500;-500;-500;-500;-500;-500;-600;-600;-600;-600;-600;-600;-600;-350;-350;-350;-350;-350;-350;-350;-450;-450;-450;-450;-450;-450;-450];
A=zeros(60,112);
for i=1;1for j=1:112A(i,j)=1;end
end
i0=0;
for i=2:4for j=i0+1:(i-1)*28A(i,j)=1;endi0=j;
end
for i=5:32for j=(i-4):28:80+iA(i,j)=1;end
end
for i=33:39for j= i-32:7:(i-11)A(i,j)=1;end
end
j0=j;
for i=40:46for j=j0+(i-39):7:(i-18)+j0A(i,j)=1;end
end
j0=j;
for i=47:53for j=j0+(i-46):7:j0+(i-25)A(i,j)=1;end
end
j0=j;
for i=54:60for j=j0+(i-53):7:j0+(i-32)A(i,j)=1;end
end
b=[362;48;125;119;17;17;17;17;17;17;17;20;20;20;20;20;20;20;15;15;15;15;15;15;15;18;18;18;18;18;18;18;12;12;12;12;12;12;12;25;25;25;25;25;25;25;17;17;17;17;17;17;17;10;10;10;10;10;10;10];
UB=[3;3;3;3;3;3;3;5;5;5;5;5;5;5;3;3;3;3;3;3;3;2;2;2;2;2;2;2;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;8;8;8;8;8;8;8;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;+inf;0;0;0;0;0;0;0];
LB=[1;1;1;1;1;1;1;2;2;2;2;2;2;2;1;1;1;1;1;1;1;1;1;1;1;1;1;1;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;2;1;1;1;1;1;1;1;1;1;1;1;1;1;1;3;3;3;3;3;3;3;1;1;1;1;1;1;1;0;0;0;0;0;0;0];
Aeq=zeros(7,112);
for i=1:7Aeq(i,i+14)=1;
end
beq=[2;2;2;2;2;2;2];
[x,fval]=linprog(f,A,b,Aeq,beq,LB,UB)
建模资料
资料分享: 最强建模资料


相关文章:

2023年国赛数学建模思路 - 复盘:人力资源安排的最优化模型
文章目录 0 赛题思路1 描述2 问题概括3 建模过程3.1 边界说明3.2 符号约定3.3 分析3.4 模型建立3.5 模型求解 4 模型评价与推广5 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 描述 …...
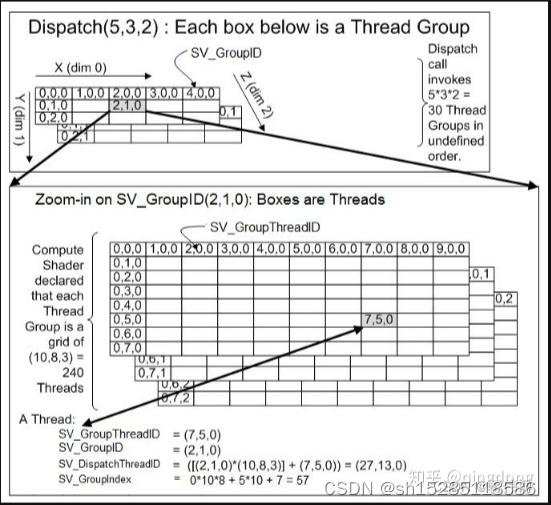
Compute shader SV 理解图
本图转子:【Computeshader】个人总结_蒋伟博的博客-CSDN博客...
生信豆芽菜-多种算法计算免疫浸润
网址:http://www.sxdyc.com/immuneInfiltration 一、使用方法 1、数据准备 一个全编码蛋白的表达谱基因,其中行为基因,列为样本 第一列为基因为行名,不能重复 2、选择计算的方法(这里提供了5种免疫计算的方法&#x…...
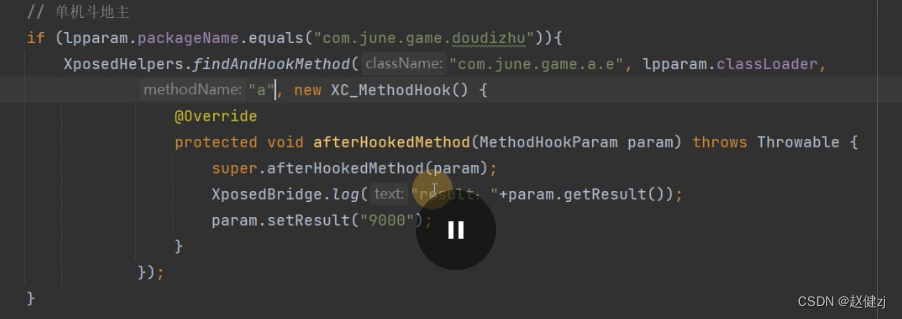
逆向破解学习-单机斗地主
试玩 破解思路 9000 是成功的代码 Hook代码 import de.robv.android.xposed.XC_MethodHook; import de.robv.android.xposed.XposedHelpers; import de.robv.android.xposed.callbacks.XC_LoadPackage; public class HookComJuneGameDouDiZhu extends HookImpl{ Override p…...

matplotlib绘制位置-时序甘特图
文章目录 1 前言2 知识点2.1 matplotlib.pyplot.barh2.2 matplotlib.legend的handles参数 3 代码实现4 绘制效果5 总结参考 1 前言 这篇文章的目的是,总结记录一次使用matplotlib绘制时序甘特图的经历。之所以要绘制这个时序甘特图,是因为22年数模研赛C…...

数据库概述、部署MySQL服务、必备命令、密码管理、安装图形软件、SELECT语法 、筛选条件
Top NSD DBA DAY01 案例1:构建MySQL服务器案例2:密码管理案例3:安装图形软件案例4:筛选条件 1 案例1:构建MySQL服务器 1.1 问题 在IP地址192.168.88.50主机和192.168.88.51主机上部署mysql服务练习必备命令的使用 …...

概率论与数理统计:第四章:随机变量的数字特征
文章目录 Ch4. 随机变量的数字特征1. 数学期望E(X)(1)数学期望的概念1.离散型①一维离散型随机变量X的数学期望: E X EX EX②一维离散型随机变量的函数的期望: E [ g ( X ) ] E[g(X)] E[g(X)]③二维离散型随机变量的函数的期望: E [ g ( X , …...

解决饿了么ui的对话框缩放和移动
import Vue from "vue";// v-dialogDrag: 弹窗拖拽水平方向伸缩 /** 使用方法* 将以下代码复制到一个js文件中,然后在入口文件main.js中import引入即可;* 给elementUI的dialog上加上 v-dialogDrag 指令就可以实现弹窗的全屏和拉伸了。* 给…...

Linux 中复制文件并保持修改时间等属性
一、遇到的问题 Linux使用cp命令复制文件备份时,发现文件的修改时间变成当前时间了,想要保留备份文件原有的修改时间及其它文件属性。 二、实现 1、cp命令 在 Linux 中,你可以使用 cp 命令来复制文件,并通过 -p 或 --preserve…...

Hugging News #0814: Llama 2 学习资源大汇总
每一周,我们的同事都会向社区的成员们发布一些关于 Hugging Face 相关的更新,包括我们的产品和平台更新、社区活动、学习资源和内容更新、开源库和模型更新等,我们将其称之为「Hugging News」。本期 Hugging News 有哪些有趣的消息࿰…...
-阶梯线图(Step Chart))
可视化绘图技巧100篇进阶篇(五)-阶梯线图(Step Chart)
目录 前言 图表类型特征 适用场景 图例 绘图工具及代码实现 ECharts SMARTBI...

GPT带我学-设计模式-命令模式
1 你知道设计模式的命令模式吗 是的,我知道设计模式中的命令模式。命令模式是一种行为型设计模式,它将请求封装成一个对象,从而允许使用不同的请求、队列或日志来参数化其他对象。命令模式还支持撤销操作,并且可以提供事务的实现…...

互联网发展历程:跨越远方,路由器的启示
互联网的蓬勃发展,一直在追求更广阔的连接,更遥远的距离。然而,在早期的网络中,人们面临着连接距离有限的问题。一项重要的技术应运而生,那就是“路由器”。 连接受限的问题:距离有限 早期的网络受限于直接…...
postman入门基础 —— 接口测试流程
一、编写接口测试计划 接口测试计划和功能测试计划目标一致,都是为了确认需求、确定测试环境、确定测试方法,为设计测试用例做准备,初步制定接口测试进度方案。一般来说,接口测试计划包括概述、测试资源、测试功能、测试重点、测试…...

springcloud+nacos实现灰度发布
灰度发布 gateway网关实现灰度路由 灰度发布实体 package com.scm.boss.common.bean;import lombok.Data; import lombok.experimental.Accessors;import java.io.Serializable;/*** 灰度发布实体*/ Data Accessors(chain true) public class GrayBean implements Serializ…...

【C++笔记】C++之类与对象(上)
【C笔记】C之类与对象(上) 1、类是结构体的升级2、类中可以定义的东西3、类访问限定符4、类的声明5、类的实例化(定义)6、类的大小的计算7、this指针 1、类是结构体的升级 C的一个显著特征就是兼容C语言,所以C把结构体“升级”成了“类”&am…...

ebay灯串UL报告 UL588检测标准
季节性和装饰性照明用品即灯串以及配件都是便携式插头连接的临时性商品,最大额定输入电压为 120 伏。 由 ILAC ISO 17025 认证的实验室出具的检测报告,确认每件商品均已经过检测,符合下列要求: 季节性和装饰性照明用品(灯串&…...
TCP/IP协议追层分析物理层(第三十九课)
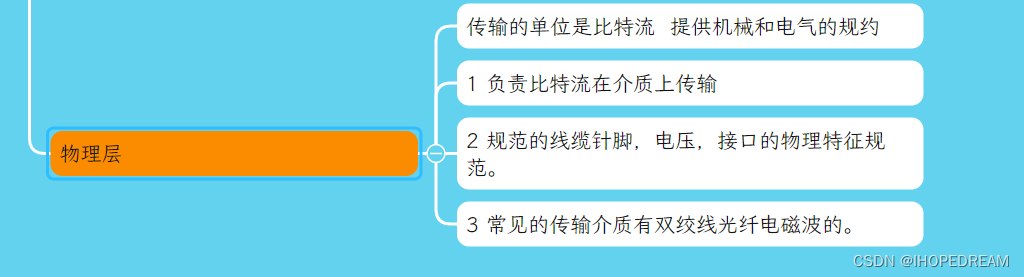
TCP/IP协议追层分析物理层(第三十九课) 1 物理层:建立、维护、断开物理连接,定义了接口及介质,实现了比特流的传输。 1、传输介质分类 有线介质:网线(双绞线)、光纤 无线介质:无线电 微波 激光 红外线 2、双绞线分类: 五类cat5: 适用于100Mbps 超五类cat5e:适用于…...
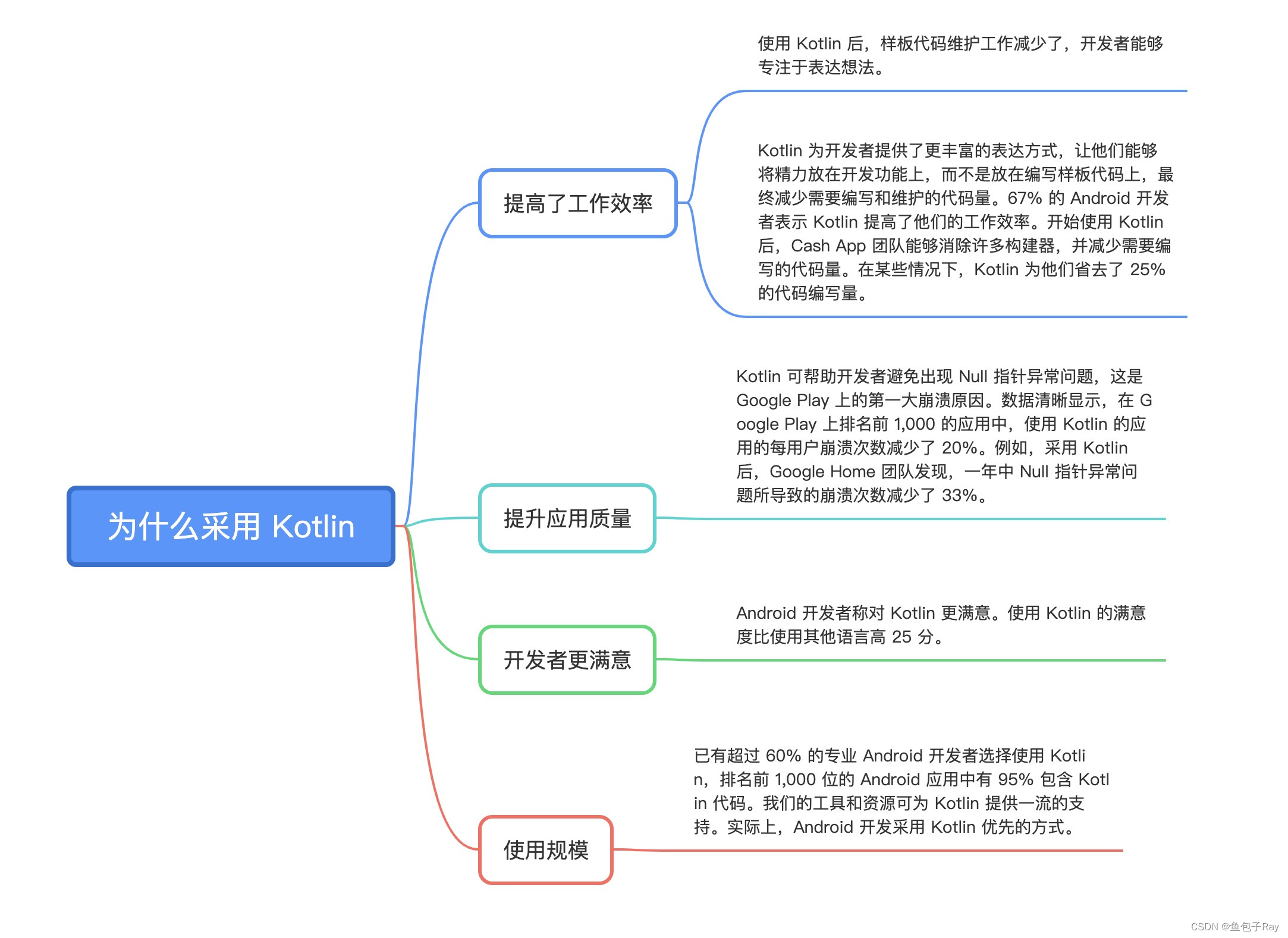
Kotlin优点及为什么使用Kotlin
文章目录 一 Hello Kotlin二 Kotlin优点三 团队为什么采用 Kotlin 一 Hello Kotlin Kotlin和Andriod 二 Kotlin优点 三 团队为什么采用 Kotlin...
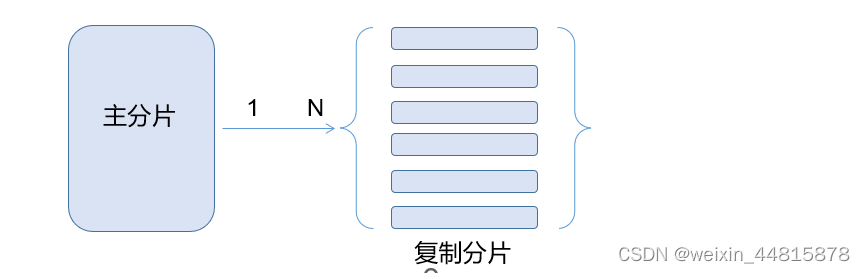
ES 概念
es 概念 Elasticsearch是分布式实时搜索、实时分析、实时存储引擎,简称(ES)成立于2012年,是一家来自荷兰的、开源的大数据搜索、分析服务提供商,为企业提供实时搜索、数据分析服务,支持PB级的大数据。 -- …...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...
