数据结构入门指南:二叉树
目录
文章目录
前言
1. 树的概念及结构
1.1 树的概念
1.2 树的基础概念
1.3 树的表示
1.4 树的应用
2. 二叉树
2.1 二叉树的概念
2.2 二叉树的遍历
前言
在计算机科学中,数据结构是解决问题的关键。而二叉树作为最基本、最常用的数据结构之一,不仅在算法和数据处理中发挥着重要作用,也在日常生活中有着丰富的应用。无论是搜索引擎的索引算法、文件系统的组织方式,还是编译器的语法分析,二叉树都扮演着不可或缺的角色。为了便于大家更好的入门二叉树,本期先向大家简单介绍一下二叉树的基本性质,以及代码理解实现,给大家预预热。
1. 树的概念及结构
1.1 树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 有一个特殊的结点,称为根结点,根节点没有前驱结点
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i<= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 因此,树是递归定义的。
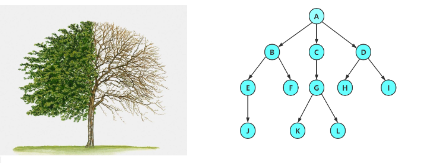
那这样是树还是非树?
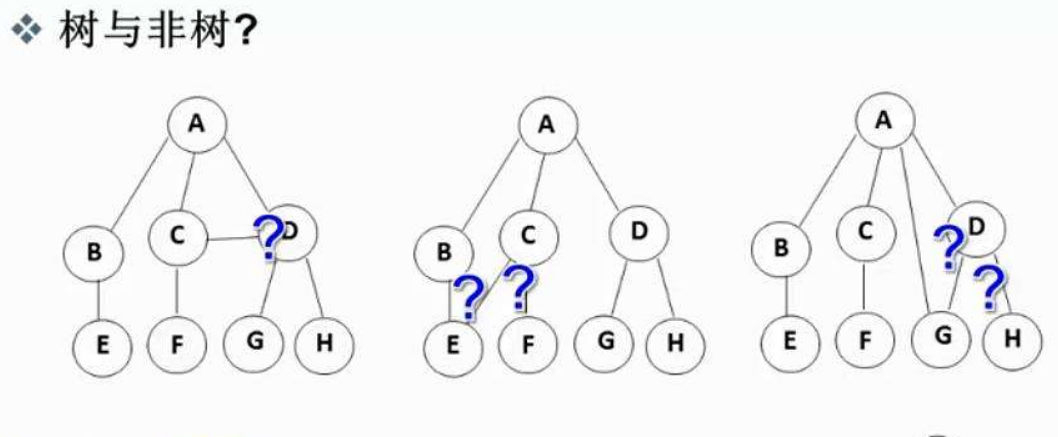
答案是非树,树形结构中,子树之间不能有交集,否则就不是树形结构。
1.2 树的基础概念
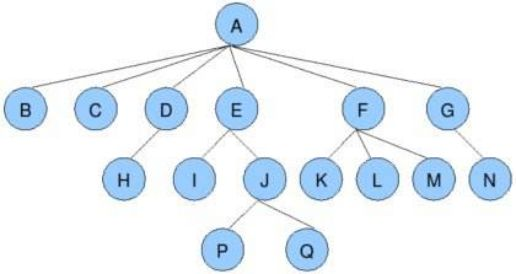
- 节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
- 叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
- *非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
- 兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
- 树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
- *节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- *树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
- *堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
- *节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
- *子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
- *森林:由m(m>0)棵互不相交的树的集合称为森林;
带星号的了解即可。
这里我们重点说一下树的高度和节点层次,不同的数据结构书中一般有两种方式表示树的高度,一种是从0开始例如上述的树,根节点A高度就是0,到P、Q高度就是3。另外一种是从1开始,根节点1的高度为1,那P、Q的高度就是4。个人更推荐使用从1开始的,如果使用从0开始的,那如果是空树,在使用0表示就有点说不过去了,那空树的高度就只能是-1了。如果使用从1开始的,那空树就可以使用0来表示。
1.3 树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。
首先在定义树的节点时就很为难,一个节点到底要定义多少个指向子节点的指针:
struct TreeNode
{Datatype x;struct TreeNode* child1;struct TreeNode* child2;……};要想定义一个节点就要先知道一个树的度,例如上述的树:

这棵树的度为6,那我们定义时就要定义6个指针变量吗?那大部分的节点的子节点并没有达到6个,这样就会很浪费,定义也很费劲。
在C++中,有这样一种定义方法:
struct TreeNode
{Datatype x;vector<struct TreeNode*> childs;
};可以不规定个数,它使用数组的方式来存储,如果不够还可以进行增容,这种方式是使用顺序表来存储孩子节点的信息。
还有一种非常巧的方式,叫孩子兄弟表示法,即左孩子右兄弟。
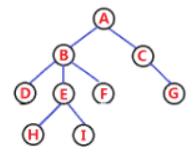
拿这棵树为例,这种方法在定义节点时就只定义两个指针,一个指针叫左孩子指针,一个指针叫右兄弟指针。怎么指向呢?就是说无论一个节点有多少个孩子,它的孩子指针就只指向第一个孩子(最左边的孩子节点),剩下的孩子用第一个孩子的兄弟指针指向第二个,第二个孩子的兄弟指针指向第三个。
表示出来就是这样的结构:
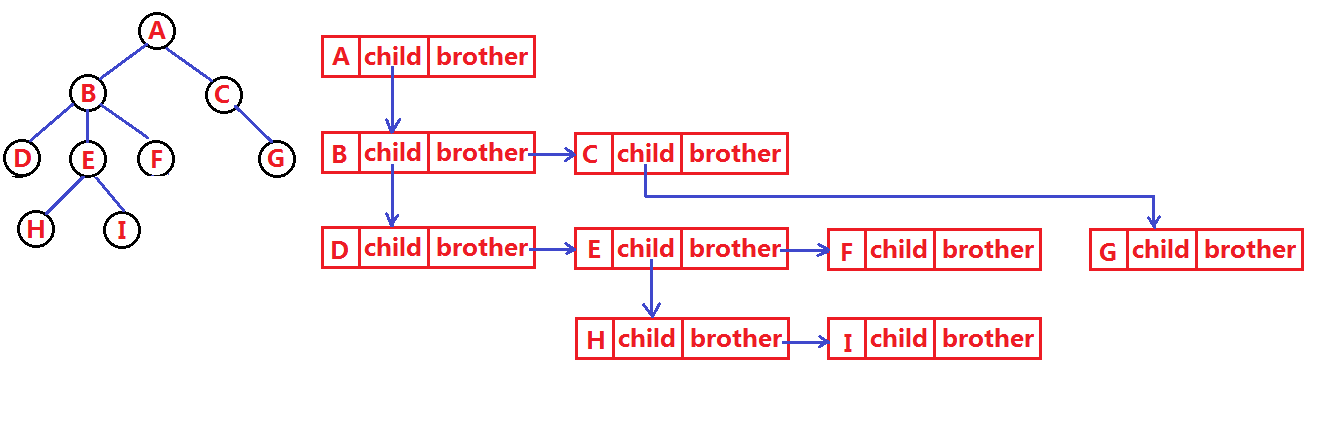 除此之外还有其他的表示法,这里就不再一一列举。
除此之外还有其他的表示法,这里就不再一一列举。
1.4 树的应用
在现实生活中我们也经常使用到树状结构,例如:文件存储
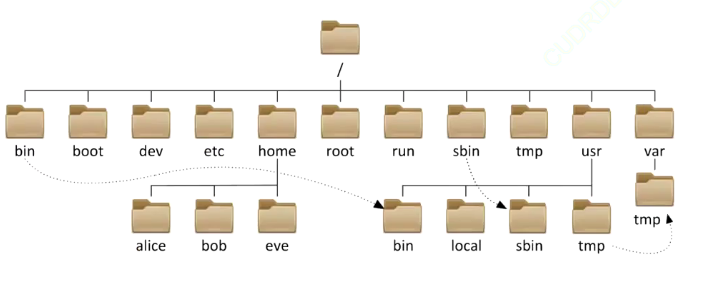
2. 二叉树
了解完树的基本概念后,我们接下来进入二叉树的学习。
2.1 二叉树的概念
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
二叉树的特点:
- 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
对于任何一颗二叉树都是由一下几种情况复合而成。
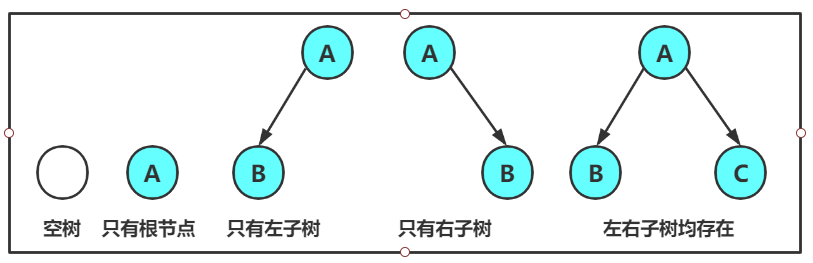
当然关于二叉树的基础概念还有很多,今天就先简单介绍,接下来给大家来点干货,先让大家切身体验一下二叉树。
2.2 二叉树的遍历
当我们看到任何一颗二叉树都应该把它分为三个部分:
- 根节点
- 左子树
- 右子树
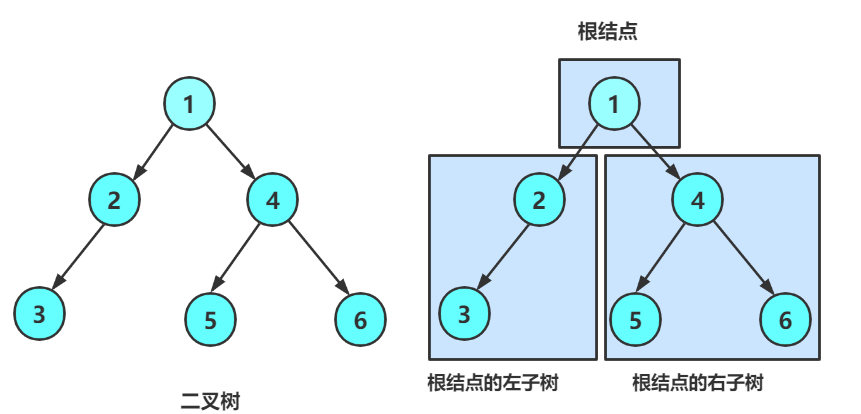
我们以这棵树为例进行分析:
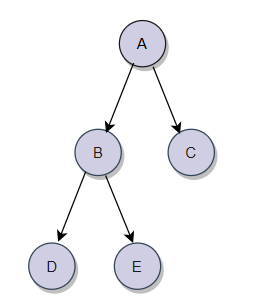
A为这棵树的根节点,B及其以下的节点(D、E)被称为左子树,C及其以下节点被称为右子树。然后B子树仍然可以分为D及其以下节点是左子树,E及其以下节点是右子树,然后再分,直到子节点为NULL,停止。
我们这里用的是分治算法。分治算法:
把大问题分成类似的子问题,子问题再分成子问题,……,直到子问题无法再分割为止。
遍历可分为三种:
前序:也叫先根遍历,遍历顺序为:根、左子树、右子树
中序:也叫中根遍历,遍历顺序为:左子树、根、右子树
后序:也叫后根遍历,遍历顺序为:左子树、右子树、根
我们先来尝试以下前序遍历,理解了前序遍历后两个就简单了。还是以这棵树为例:

前序遍历,我们是先访问根,然后是左子树、右子树。那应该先遍历A,然后遍历A的左子树B(及其以下节点),然后就以B为根继续遍历它的左子树D(及其以下节点),然后再次以D为根开始,遍历左子树(NULL),然后开始返回到D,D再遍历右子树(NULL),然后D(这个子树)就遍历完毕,返回到B,B开始遍历右子树E(及其以下节点),E左子树为NULL返回到E,然后遍历右子树,右子树也为空(E子树遍历完毕),然后返回E(B的右子树遍历完毕),接着返回B(B的所有子树遍历完毕),接着返回到A,A开始遍历右子树……这个规律很符合递归。
遍历完的顺序为:A、B、D、NULL、NULL、E、NULL、NULL、C、NULL、NULL。大部分学校讲的都是A、B、D、E、C。大部分同学应该都知道这个规律,但不知道为什么这样遍历。
根据这个思路我们再来写一下中序遍历,中序遍历先访问左子树,然后是跟,最后是右子树。还是从A开始找,A的左子树B,然后以B为根,找B的左子树,接着以D为根,找D的左子树,D的左子树为NULL(D左子树遍历结束),返回到D(根),开始遍历D的右子树……

最后遍历的顺序为:【NULL、D、NULL(B的左子树)、B(根)、NULL、E、NULL (B的右子树)、】(A的左子树)、A(根)、【NULL、C、NULL】(A的右子树)。整理一下:
NULL、D、NULL、B、NULL、E、NULL、A、NULL、C、NULL(D、B、E、C、A)。
我们接着写一下后序遍历:NULL、NULL、D、NULL、NULL、E、B、NULL、NULL、C、A(D、E、B、C、A)。
我们再来练一个:
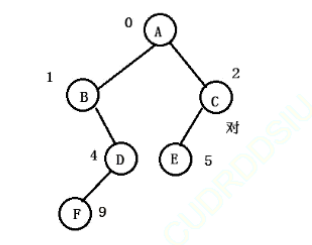
前序遍历:A(根)||这部分为整体二叉树的根、B(左子树)、NULL(B的左子树)、D(B的右子树)、F(D的左子树)、NULL(F的左子树)、NULL(F的右子树)、NULL(D的右子树)||这部分属于A的左子树、C、E、NULL(E的左子树)、NULL(E的右子树)、NULL(C的右子树)||这部分为A的右子树。
后续的中序遍历和后续遍历大家可以自己私下练一下。
好了我们已经了解了遍历,接下来我们来说实现以下前序遍历。给大家来点干货,便于大家更好理解。
我们依然以这个简单的二叉树为例进行实现。

我们先定义一个二叉树的节点:
typedef char Datatype;
typedef struct BinaryTreeNode
{Datatype data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
然后就是它的前序遍历的实现:
void PrevOrder(BTNode* root)
{}我们知道前序遍历的顺序是根,然后是左子树,最后是右子树。因此在开始前我们先判断以下root是否为NULL,如果不为NULL我们就打印根节点的数据。
void PrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ", root->data);}那如何遍历到左子树、右子树呢?其实很简单,我们之前介绍的时候说:二叉树的遍历复合递归结构,这里我们就可以使用递归来完成遍历,代码如下:
void PrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}先遍历左子树,再遍历右子树,那调用的顺序就先调用自己传左孩子指针过去,以左孩子节点为根,再按照这个程序进行执行,再次传左孩子指针过去……,知道左孩子为NULL,返回上一层,开始遍历右子树。
我们可以简单粗暴的测试以下,测试代码如下:
#include<stdio.h>
#include<stdlib.h>typedef char Datatype;
typedef struct BinaryTreeNode
{Datatype data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;void PrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}
int main()
{BTNode* A = (BTNode*)malloc(sizeof(BTNode));A->data = 'A';A->left = NULL;A->right = NULL;BTNode* B = (BTNode*)malloc(sizeof(BTNode));B->data = 'B';B->left = NULL;B->right = NULL;BTNode* C = (BTNode*)malloc(sizeof(BTNode));C->data = 'C';C->left = NULL;C->right = NULL;BTNode* D = (BTNode*)malloc(sizeof(BTNode));D->data = 'D';D->left = NULL;D->right = NULL;BTNode* E = (BTNode*)malloc(sizeof(BTNode));E->data = 'E';E->left = NULL;E->right = NULL;A->left = B;A->right = C;B->left = D;B->right = E;PrevOrder(A);printf("\n");return 0;
}执行结果:

和上述分析的结果一致。
那剩下的中序遍历和后序遍历也很简单,只需要改变一下递归调用函数的次序即可:
//中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);
}//后序遍历
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%c ", root->data);}我们也可以测试以下看看执行结果,测试代码如下:
typedef struct BinaryTreeNode
{Datatype data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;void PrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);
}
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%c ", root->data);}
int main()
{BTNode* A = (BTNode*)malloc(sizeof(BTNode));A->data = 'A';A->left = NULL;A->right = NULL;BTNode* B = (BTNode*)malloc(sizeof(BTNode));B->data = 'B';B->left = NULL;B->right = NULL;BTNode* C = (BTNode*)malloc(sizeof(BTNode));C->data = 'C';C->left = NULL;C->right = NULL;BTNode* D = (BTNode*)malloc(sizeof(BTNode));D->data = 'D';D->left = NULL;D->right = NULL;BTNode* E = (BTNode*)malloc(sizeof(BTNode));E->data = 'E';E->left = NULL;E->right = NULL;A->left = B;A->right = C;B->left = D;B->right = E;printf("前序遍历:");PrevOrder(A);printf("\n");printf("中序遍历:");InOrder(A);printf("\n");printf("后序遍历:");PostOrder(A);printf("\n");return 0;
}执行结果如下:

可以和上边的分析对比一下,没有问题,
总结
二叉树遍历是学习和理解二叉树的重要部分。通过遍历,我们可以按照特定的顺序访问二叉树的节点,从而深入了解它们的结构和关系。在这篇博客中,我们介绍了三种常见的二叉树遍历方式:前序遍历、中序遍历和后序遍历,并对它们的原理、特点和应用进行了详细讨论。本期内容为预热阶段,先让大家熟悉一下二叉树,以便于后续二叉树的学习,好的本期内容到此结束,感谢阅读!
相关文章:

数据结构入门指南:二叉树
目录 文章目录 前言 1. 树的概念及结构 1.1 树的概念 1.2 树的基础概念 1.3 树的表示 1.4 树的应用 2. 二叉树 2.1 二叉树的概念 2.2 二叉树的遍历 前言 在计算机科学中,数据结构是解决问题的关键。而二叉树作为最基本、最常用的数据结构之一,不仅在算法…...

大数据课程J2——Scala的基础语法和函数
文章作者邮箱:yugongshiyesina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 掌握Scala的基础语法; ⚪ 掌握Scala的函数库; 一、Scala 基础语法一 1. 概述 语句 说明 示例 var 用来声明一个变量, 变量声明后…...
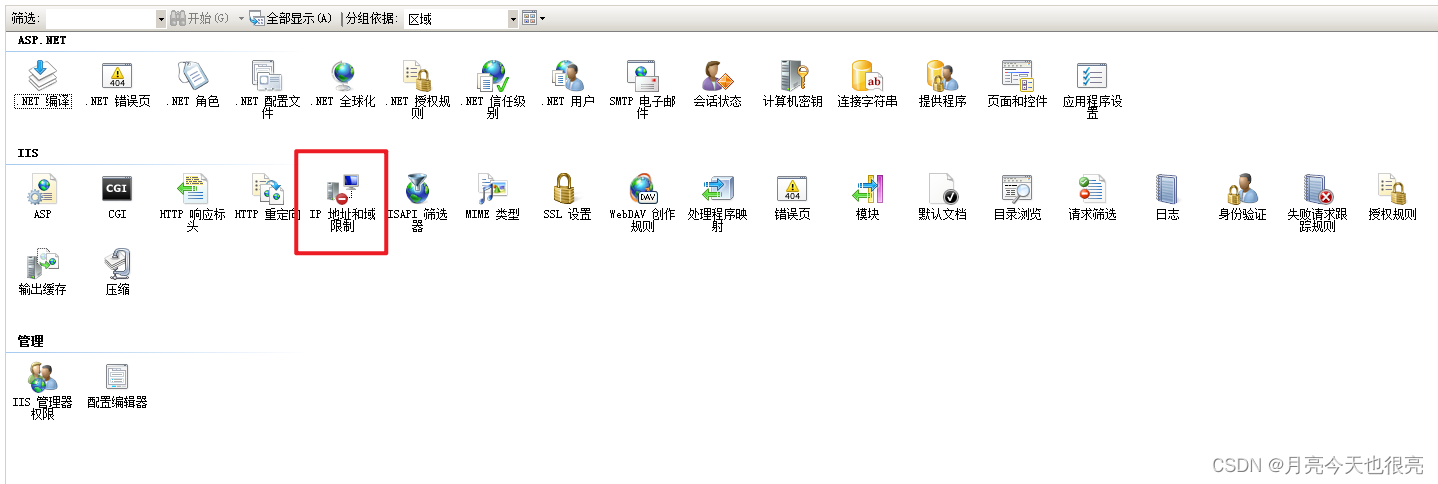
03-基础入门-搭建安全拓展
基础入门-搭建安全拓展 1、涉及的知识点2、常见的问题3、web权限的设置4、演示案例-环境搭建(1)PHPinfo(2)wordpress(3)win7虚拟机上使用iis搭建网站(4)Windows Server 2003配置WEB站…...

穿越未来:探索虚拟现实科技的未来前景
虚拟现实(Virtual Reality,简称VR)科技,正如一颗崭新的明星,迅猛崛起,为人类带来前所未有的体验和想象空间。随着科技的飞速发展,VR 科技的未来充满了无限的可能性,正将我们引向一个…...
SQL- 每日一题【1327. 列出指定时间段内所有的下单产品】
题目 表: Products 表: Orders 写一个解决方案,要求获取在 2020 年 2 月份下单的数量不少于 100 的产品的名字和数目。 返回结果表单的 顺序无要求 。 查询结果的格式如下。 示例 1: 解题思路 1.题目要求我们获取在 2020 年 2 月份下单的数量不少于 100 的产品的…...

[xgb] plot tree
xgboost plot tree debug problem1solutionsreference problem2solutionreference problem3solutionreference supplementary explanationplot_tree参数介绍num_treesmodel.get_booster().best_iteration图中信息介绍缺失值叶子的值 训练的XGB模型里有多少棵树 problem1 用xgb…...

【云原生】Kubernetes 概述
Kubernetes 概述 1.Kubernetes 简介 Kubernetes 是一个可移植的、可扩展的、用于管理容器化工作负载和服务的开源平台,它简化(促进)了声明式配置和自动化。它有一个庞大的、快速增长的生态系统。Kubernetes 的服务、支持和工具随处可见。 K…...

9.2.2Socket(TCP)
一.过程: 1.建立连接(不是握手),虽然内核中的连接有很多,但是在应用程序中,要一个一个处理. 2. 获取任务:使用ServerSocket.accept()方法,作用是把内核中的连接获取到应用程序中,这个过程类似于生产者消费者模型. 3. 使用缓冲的时候,注意全缓冲和行缓冲. 4.注意关闭文件资源…...
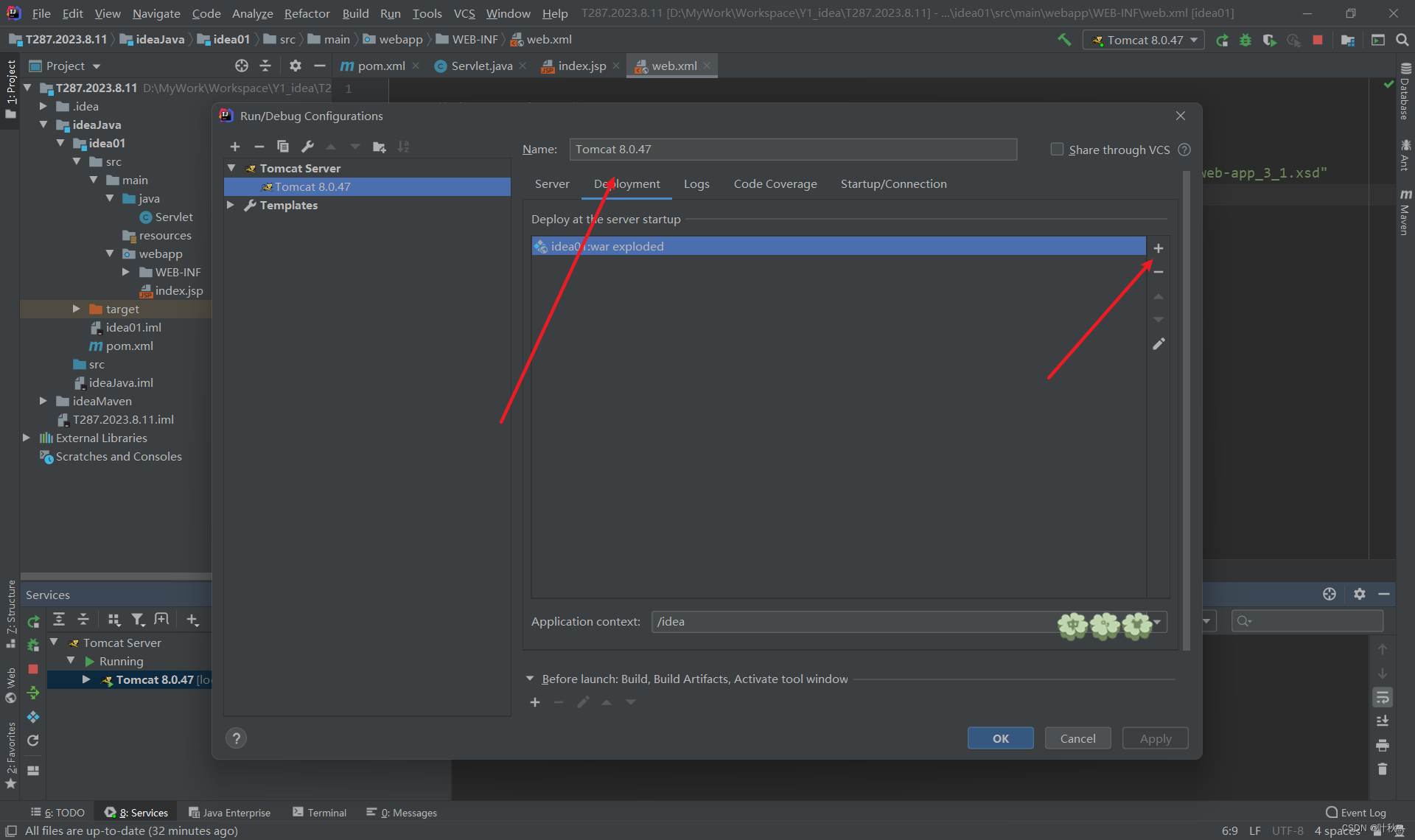
“解锁IDEA的潜力:高级Java Maven项目配置指南”
目录 前言:流程目录:1.确保Java和Maven已安装检查Java是否已正确安装并配置环境变量 2.创建一个新的Maven项目导航到要创建项目的目录配置Maven运行以下命令创建一个新的Maven项目 3.配置项目的pom.xml文件打开项目根目录下的pom.xml文件配置Web.xml 4.配…...
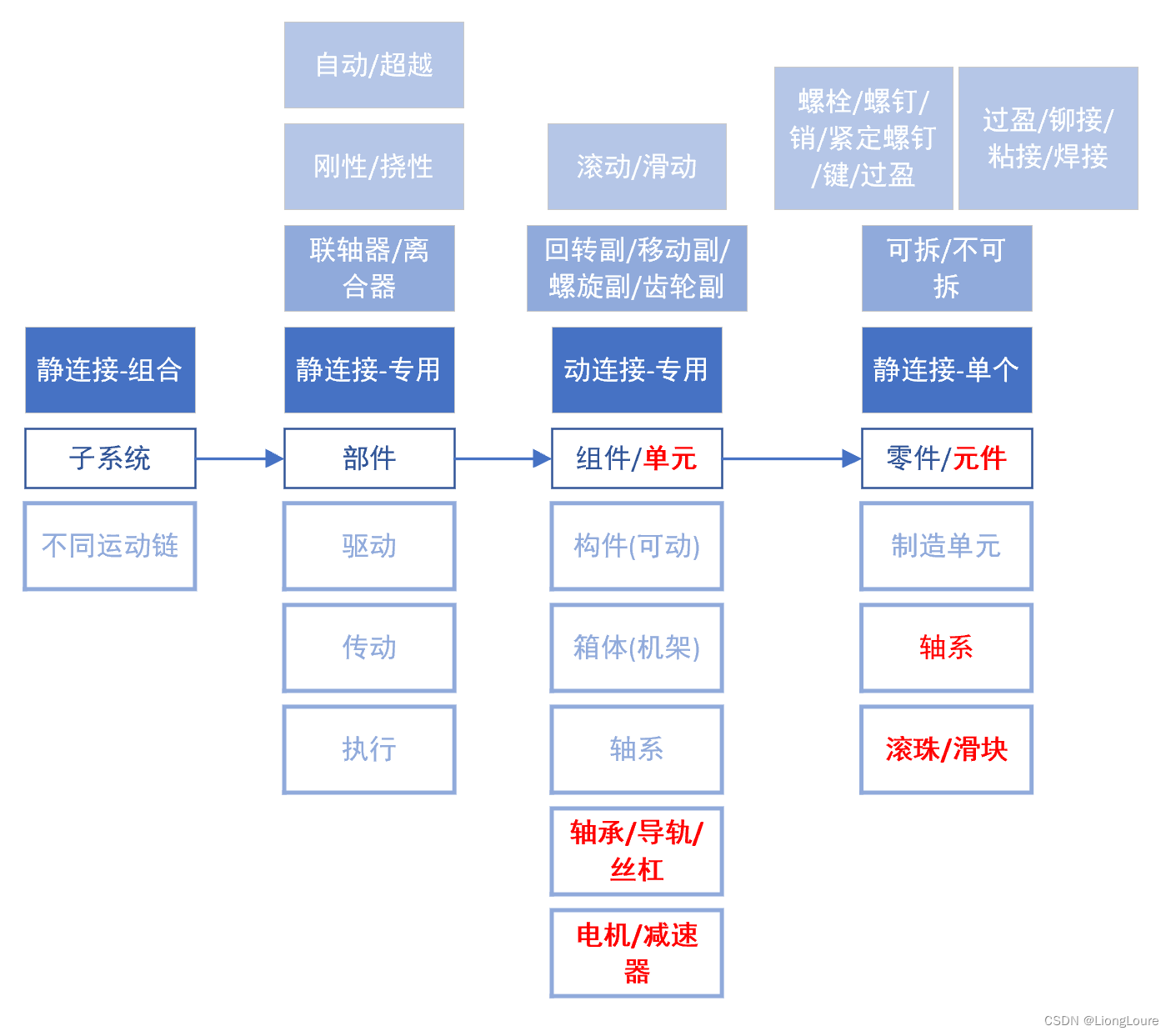
[足式机器人]Part5 机械设计 Ch00/01 绪论+机器结构组成与连接 ——【课程笔记】
本文仅供学习使用 本文参考: 《机械设计》 王德伦 马雅丽课件与日常作业可登录网址 http://edu.bell-lab.com/manage/#/login,选择观摩登录,查看2023机械设计2。 机械设计-Ch00Ch01——绪论机器结构组成与连接 Ch00-绪论0.1 何为机械设计——…...
)
机器学习:隐马尔可夫模型(HMM)
后续会回来补充代码 1 隐马尔可夫模型 隐马尔可夫模型(Hidden Markov Model,HMM)是可用于标注问题的统计学模型,描述由隐藏的马尔可夫链随机生成观测序列的过程。 1.1 数学定义 隐马尔可夫模型是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成…...

使用插件实现pdf,word预览功能
效果 代码: 插件地址: https://github.com/501351981/vue-office <a-modalv-model:visible"visible":title"title"ok"handleOk":bodyStyle"bodyStyle":width"1200":maskClosable"false"…...
)
yolov5模型构建源码详细解读(yaml、parse_model等内容)
文章目录 前言一、yolov5文件说明二、yolov5调用模型构建位置三、模型yaml文件解析1、 yaml的backbone解读Conv模块参数解读C3模块参数解读 2、yaml的head解读Concat模块参数解读Detect模块参数解读 四、模型构建整体解读五、构建模型parse_model源码解读 前言 本文章记录yolo…...

Monodepth2和Lite-Mono准备数据集
以KITTI为例下载解压后放在/home/lwd/tmp/2011_09_26 cd /home/lwd/tmp/2011_09_26 ls输出 2011_09_26_drive_0001_sync 2011_09_26_drive_0002_sync 2011_09_26_drive_0005_sync python txt.py txt.py import os, sysalos.listdir(.) al.sort() fopen(train.txt, w) for a in…...

ML-fairness-gym入门教学
1、ML-fairness-gym简介 ML-fairness-gym是一个探索机器学习系统长期影响的工具。可以用于评估机器学习系统的公平性和评估静态数据集上针对各种输入的误差度量的差异。开源网站:GitHub - google/ml-fairness-gym 2、安装ML-fairness-gym(Windows&…...

结构体指针变量的使用
1、结构体指针的引用 #include<iostream> using namespace std;struct Student {int num;char name[32]; }; int main() {struct Student stu {1,"张三"};struct Student* p &stu;system("pause"); return 0; } 2、通过结构体指针访问结构体…...

解决oracle的em访问提示“使用不受支持的协议。”的bug
1. 设置oracle唯一名称 执行emctl时需要设置一个唯一的名称 否则提示 “Environment variable ORACLE_UNQNAME not defined. Please set ORACLE_UNQNAME to database unique name. ”中文意思为“未定义环境变量ORACLE_UNQNAME。 请将ORACLE_UNQNAME设置为数据库唯一名称/服务…...
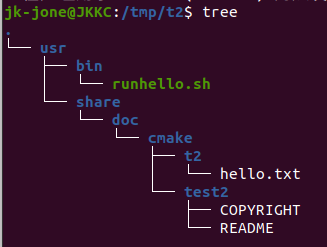
编译工具:CMake(三)| 最简单的实例升级
编译工具:CMake(三)| 最简单的实例升级 前言过程语法解释ADD_SUBDIRECTORY 指令 如何安装目标文件的安装普通文件的安装:非目标文件的可执行程序安装(比如脚本之类)目录的安装 修改 Helloworld 支持安装测试 前言 本篇博客的任务…...
常见系统库的使用)
20天学会rust(四)常见系统库的使用
前面已经学习了rust的基础知识,今天我们来学习rust强大的系统库,从此coding事半功倍。 集合 数组&可变长数组 在 Rust 中,有两种主要的数组类型:固定长度数组(Fixed-size Arrays)和可变长度数组&…...
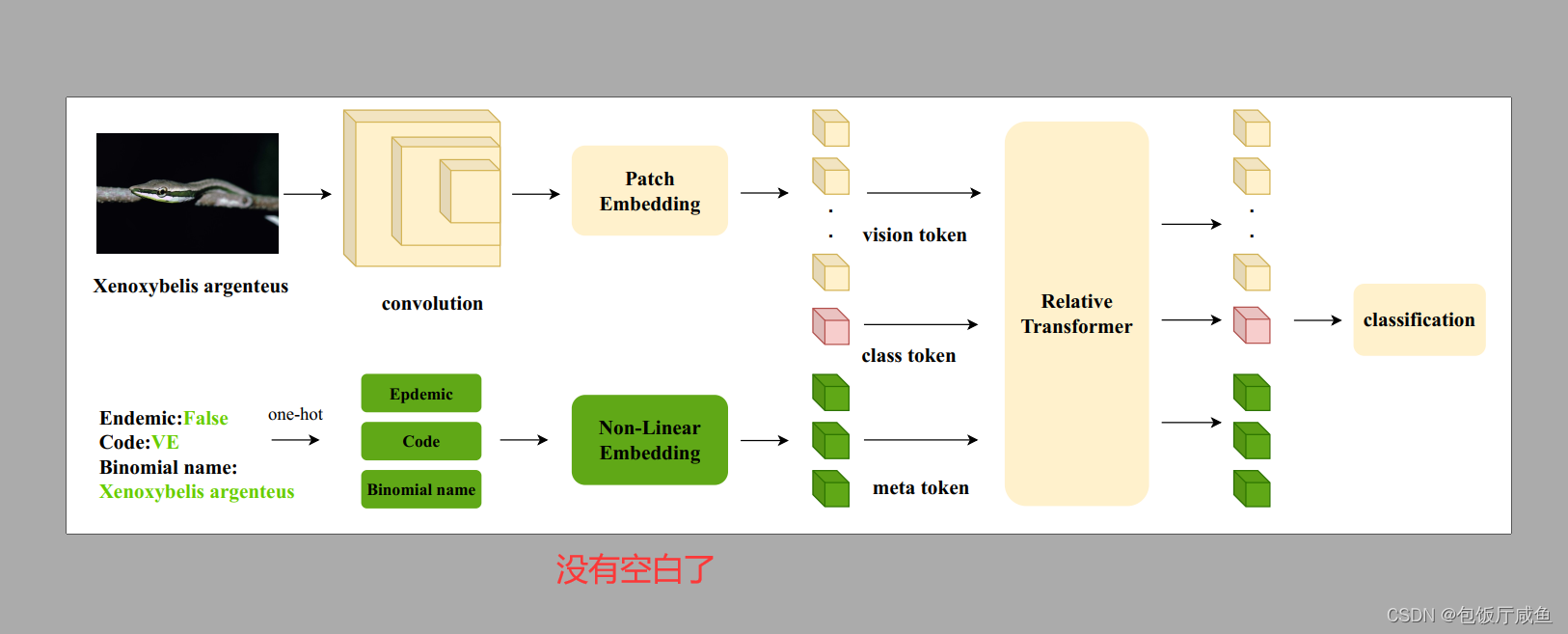
drawio----输出pdf为图片大小无空白(图片插入论文)
自己在写论文插入图片时为了让论文图片放大不模糊,啥方法都试了,最后摸索出来这个。 自己手动画图的时候导出pdf总会出现自己的图片很小,pdf的白边很大如下如所示,插入论文的时候后虽然放大不会模糊,但是白边很大会显…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
