DIP:《Deep Image Prior》经典文献阅读总结与实现

文章目录
- Deep Image Prior
- 1. 方法原理
- 1.1 研究动机
- 1.2 方法
- 2. 实验验证
- 2.1 去噪
- 2.2 超分辨率
- 2.3 图像修复
- 2.4 消融实验
- 3. 总结
Deep Image Prior
1. 方法原理
1.1 研究动机
动机
- 深度神经网络在图像复原和生成领域有非常好的表现一般归功于神经网络学习到了图像的先验信息
- 网络结构本身是否具有先验信息呢?
挑战
- 如何验证网络结构本身是否具有先验信息?
- 无训练集,无未退化的原图作为标签,使用单张退化的图像进行恢复
- 唯一的先验信息来自于网络结构本身
贡献
- 发现了神经网络结构对自然信号的低阻抗性和对噪声信号具有高阻抗的隐式先验信息
- 在去噪、超分辨率、图像修复等任务上利用这种隐式先验信息实现了非常好的效果
- 网络仅仅使用退化的单个图像进行训练,所以没有大量数据集带来的图像先验信息,而是网络结构自身所具有的结构先验信息
1.2 方法
使用一个随机向量 z ∈ R c ′ × H ′ × W ′ z \in R^{c' \times H' \times W'} z∈Rc′×H′×W′,和一个神经网络( f θ ( . ) f_{\theta}(.) fθ(.))输出一个我们想要的图像 x ∈ R 3 × H × W x \in R^{3 \times H\times W} x∈R3×H×W
x = f θ ( z ) x = f_{\theta}(z) x=fθ(z)
然后,针对一个具体的 去噪、超分辨率或图像修复的问题,这就变为了一个最小化能量的问题(最大似然)
x ∗ = m i n x E ( x ; x 0 ) + R ( x ) x^* = \underset{x}{min}E(x;x_0) + R(x) x∗=xminE(x;x0)+R(x)
其中 m i n x E ( x ; x 0 ) \underset{x}{min}E(x;x_0) xminE(x;x0)是和任务相关的数据匹配项,而 R ( x ) R(x) R(x)是一个正则项。正则项目可以是简单的TV正则化,在本文中想要证明的就是网络结构本身就具有类似于TV正则化的效果,也就是:
x ∗ = m i n x E ( f θ ( z ) ; x 0 ) x^* = \underset{x}{min}E(f_{\theta}(z);x_0) x∗=xminE(fθ(z);x0)
为了最小化能量,我们可以从观测数据 z z z出发,或者从网络本身出发。DIP考虑的是只从网络结构本身探讨这个问题。
用一个最简单的重构损失来验证:我们使用一个网络参数化图像,然后最小化重构图像和真实图像的损失:
E ( x ; x 0 ) = ∣ ∣ x − x 0 ∣ ∣ 2 E(x;x_0) = ||x - x_0||^2 E(x;x0)=∣∣x−x0∣∣2
m i n θ ∣ ∣ f θ ( z ) − x 0 ∣ ∣ \underset{\theta}{min}||f_{\theta}(z) - x_0|| θmin∣∣fθ(z)−x0∣∣
使用不同的 x 0 x_0 x0进行验证:
- 真实图片作为 x 0 x_0 x0
- 真实图片+噪声作为 x 0 x_0 x0
- 真实图片像素点随机打乱作为 x 0 x_0 x0
- 噪声作为 x 0 x_0 x0

从上面这幅图中可以发现,相同的神经网络对不同的数据进行恢复,如果是真实自然图片网络可以非常快地进行恢复,而对于噪声网络的恢复在迭代很多次之后才能恢复。这展现出一种网络结构的特性:对信号具有低阻抗,而对随机噪声具有高阻抗。因此我们可以在训练过程中使用 early stopping方法,在迭代一定次数后得到的图片的信号信息。
2. 实验验证
2.1 去噪

迭代2400次的时候自然信息就基本拟合了,没有出现拟合噪声信息。
迭代50k的时候就拟合了噪声信息。
和其他方法进行对比

2.2 超分辨率

2.3 图像修复


2.4 消融实验


3. 总结
关键点
- 神经网络对自然信息具有低阻性,对随机噪声具有高阻性
- 神经网络提供的隐式先验信息可以用来进行去噪、图像修复、超分辨率
优势
- 不需要预训练网络,不需要准备训练数据集
- 可以同时解决多种问题
问题
- 速度慢,处理一个工作需要迭代上千次
- 性能不稳定,对不同的噪声达到较好效果的迭代次数不同
- 怎么确定终止次数是一个重要问题
- 没有从理论上证明这种方法的可靠性(后续有其他文章证明)
相关文章:

DIP:《Deep Image Prior》经典文献阅读总结与实现
文章目录 Deep Image Prior1. 方法原理1.1 研究动机1.2 方法 2. 实验验证2.1 去噪2.2 超分辨率2.3 图像修复2.4 消融实验 3. 总结 Deep Image Prior 1. 方法原理 1.1 研究动机 动机 深度神经网络在图像复原和生成领域有非常好的表现一般归功于神经网络学习到了图像的先验信息…...
LAXCUS如何通过技术创新管理数千台服务器
随着互联网技术的不断发展,服务器已经成为企业和个人获取信息、进行计算和存储的重要工具。然而,随着服务器数量的不断增加,传统的服务器管理和运维方式已经无法满足现代企业的需求。LAXCUS做为专注服务器集群的【数存算管】一体化平台&#…...
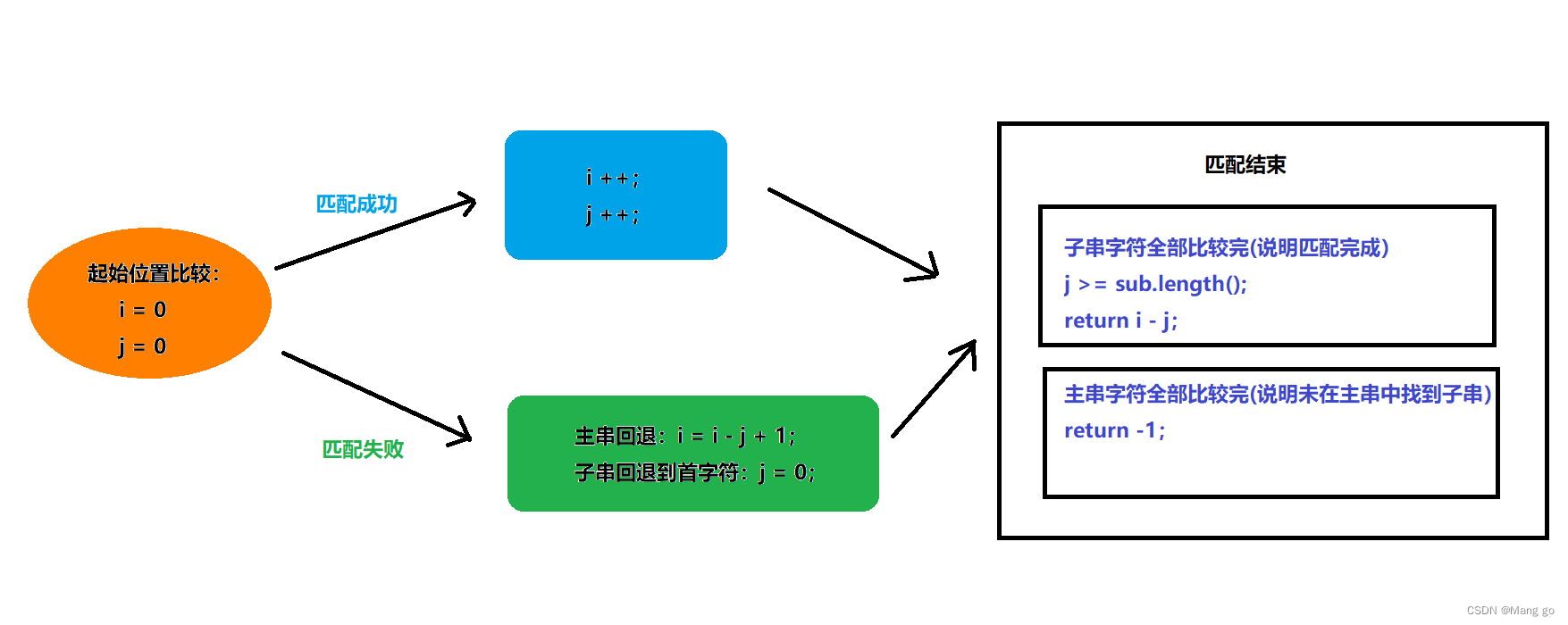
【Java】BF算法(串模式匹配算法)
☀️ 什么是BF算法 BF算法,即暴力算法,是普通的模式匹配算法,BF算法的思想就是将目标串S的第一个与模式串T的第一个字符串进行匹配,若相等,则继续比较S的第二个字符和T的第二个字符;若不相等,则…...
方法并行执行多个请求)
Vue:使用Promise.all()方法并行执行多个请求
在Vue中,可以使用Promise.all()方法来并行执行多个请求。当需要同时执行多个异步请求时,可以将这些请求封装为Promise对象并使用Promise.all()方法来执行它们。 示例1: 以下是一个示例代码,展示了如何通过Promise.all()方法并行…...

21.0 CSS 介绍
1. CSS层叠样式表 1.1 CSS简介 CSS(层叠样式表): 是一种用于描述网页上元素外观和布局的样式标记语言. 它可以与HTML结合使用, 通过为HTML元素添加样式来改变其外观. CSS使用选择器来选择需要应用样式的元素, 并使用属性-值对来定义这些样式.1.2 CSS版本 CSS有多个版本, 每个…...
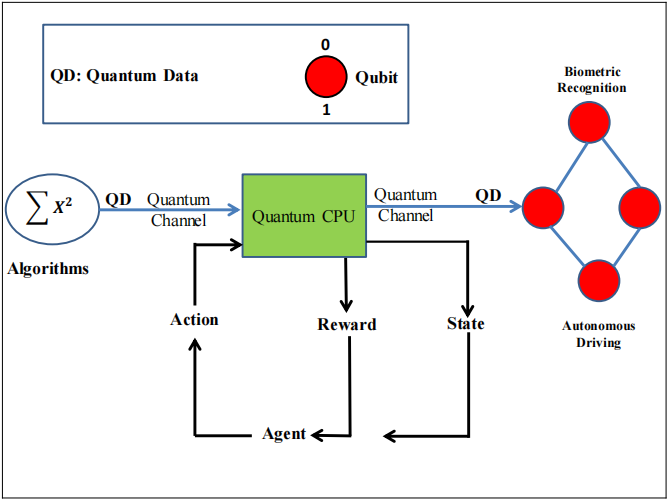
下一代计算:嵌入AI的云/雾/边缘/量子计算
计算系统在过去几十年中推动了计算机科学的发展,现在已成为企业世界的核心,提供基于云计算、雾计算、边缘计算、无服务器计算和量子计算的服务。现代计算系统解决了现实世界中许多需要低延迟和低响应时间的问题。这有助于全球各地的青年才俊创办初创企业…...

Gitlab-第四天-CD到k8s集群的坑
一、.gitlab-ci.yml #CD到k8s集群的 stages: - deploy-test build-image-deploy-test: stage: deploy-test image: bitnami/kubectl:latest # 使用一个包含 kubectl 工具的镜像 tags: - k8s script: - ls -al - kubectl apply -f deployment.yaml # 根据实际情况替换…...

【Java基础】Java对象的生命周期
【Java基础】Java对象的生命周期 一、概述 一个类通过编译器将一个Java文件编译为Class字节码文件,然后通过JVM中的解释器编译成不同操作系统的机器码。虽然操作系统不同,但是基于解释器的虚拟机是相同的。java类的生命周期就是指一个class文件加载到类…...

【每日一题】88. 合并两个有序数组
【每日一题】88. 合并两个有序数组 88. 合并两个有序数组题目描述解题思路 88. 合并两个有序数组 题目描述 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 …...

Navicat Premium连接sqlserve数据库失败?你需要注意这几点看看配置对了么?
新建数据库连接的时候这么填的信息 报错 原因1:sqlserver数据库的端口和IP地址之间不是:连接而是用,连接 改成如下样式用逗号连接端口和IP地址就好了 原因2:在Navicat Premium中需要安装一个sqlserver的插件 找到安装路径的根目…...
207、仿真-51单片机脉搏心率与血氧报警Proteus仿真设计(程序+Proteus仿真+配套资料等)
毕设帮助、开题指导、技术解答(有偿)见文未 目录 一、硬件设计 二、设计功能 三、Proteus仿真图 四、程序源码 资料包括: 需要完整的资料可以点击下面的名片加下我,找我要资源压缩包的百度网盘下载地址及提取码。 方案选择 单片机的选择 方案一&a…...
flutter 初识(开发体验,优缺点)
前言 最近有个跨平台桌面应用的需求,需要支持 windows/linux/mac 系统,要做个更新应用的小界面,主要功能就是下载更新文件并在本地进行替换,很简单的小功能。 花了几分钟构建没做 UI 优化的示例界面: 由于我们的客…...

校验vue prop的几种方式
校验vue prop的几种方式 vue 要求将传递给组件的任何数据显式声明为 props。此外,它还提供了强大的内置机制来验证该数据。这充当组件和父级组件之间的约定,并确保组件能按预期使用。 让我们看看怎么对props进行校验。它可以帮助我们在开发和调试过程中…...

vue+springboot 前后端分离 上传文件处理后再下载,并且传递参数
vue代码 <template><div><input type"file" ref"fileInput" accept".json"/><el-button click"upload">上传</el-button></div> </template><script> export default {name: "…...

【Linux操作系统】举例解释Linux系统编程中文件io常用的函数
在Linux系统编程中,文件IO操作是非常常见和重要的操作之一。通过文件IO操作,我们可以打开、读取、写入和关闭文件,对文件进行定位、复制、删除和重命名等操作。本篇博客将介绍一些常用的文件IO操作函数。 文章目录 1. open()1.1 原型、参数及…...

Ubuntu和centos版本有哪些区别
Ubuntu和CentOS是两个非常流行的Linux发行版,它们在一些方面有一些区别,如下所示: CentOS的版本发布周期相对较长,主要是因为它是基于RedHatEnterpriseLinux(RHEL)的。这意味着在RHEL发布后才能推出对应的CentOS版本。而Ubuntu则在…...

Netty:ChannelHandler抛出异常,对应的channel被关闭
说明 使用Netty框架构建的socket服务端在处理客户端请求时,每接到一个客户端的连接请求,服务端会分配一个channel处理跟该客户端的交互。如果处理该channel数据的ChannelHandler抛出异常没有捕获,那么该channel会关闭。但服务端和其它客户端…...

pytest结合 allure 打标记之的详细使用
前言 前面我们提到使用allure 可以生成漂亮的测试报告,下面就Allure 标记我们做详细介绍。 allure 标记 包含:epic,feature, story, title, testcase, issue, description, step, serverity, link, attachment 常用的标记 allure.feature…...
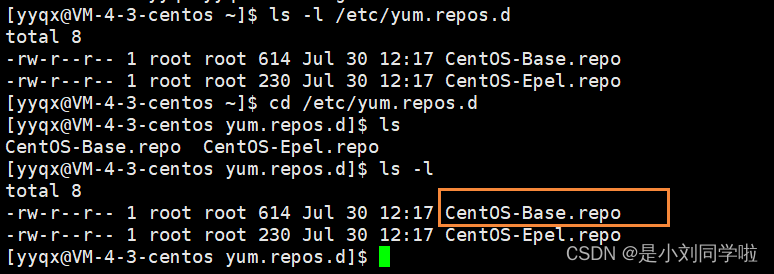
【linux】2 软件管理器yum和编辑器vim
目录 1. linux软件包管理器yum 1.1 什么是软件包 1.2 关于rzsz 1.3 注意事项 1.4 查看软件包 1.5 如何安装、卸载软件 1.6 centos 7设置成国内yum源 2. linux开发工具-Linux编辑器-vim使用 2.1 vim的基本概念 2.2 vim的基本操作 2.3 vim正常模式命令集 2.4 vim末行…...

Angular中的ActivatedRoute和Router
Angular中的ActivatedRoute和Router解释 在Angular中,ActivatedRoute和Router是两个核心的路由服务。他们都提供可以用来检查和操作当前页面路由信息的方法和属性。 ActivatedRoute ActivatedRoute是一个保存关于当前路由状态(如路由参数、查询参数以…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
