筛法求欧拉函数
思路:
(1)若要分别求1~n每个数的欧拉函数值,则复杂度O(n*n^0.5),超时;
(2)于是考虑用欧拉筛进行求取;
(3)欧拉筛:基于线性筛,在筛质数与合数过程中,递推求取欧拉值:
- 对于质数x,欧拉值为x - 1,因为除其自身外,1~n - 1均与其互质;
- 对于合数i,如果i%primes[j] == 0,则i*primes[j]与i质因子相同,于是有ph[i*primes[j] ] = ph[i]*primes[j];如果i%primes[j] != 0;则i*primes[j]与i质因子差一个质数primes[j],于是有ph[i*primes[j] ] = ph[i]*(primes[j] - 1)/primes[j] *primes[j];
代码:
#include<bits/stdc++.h>using namespace std;
typedef long long LL;
const int N = 1e6 + 10;
LL primes[N],ph[N],st[N],cnt;void euler(int n)
{ph[1] = 1;for(int i = 2;i <= n;i ++){if(st[i] == 0){primes[cnt ++] = i;ph[i] = i - 1;}for(int j = 0; primes[j]*i <= n;j ++){st[primes[j] * i ] = 1;if(i % primes[j] == 0){ph[primes[j] * i] = ph[i] * primes[j];break;}ph[primes[j] * i] = ph[i] * (primes[j] - 1);}}LL res = 0;for(int i = 1;i <= n;i ++){res += ph[i];}cout << res;
}int main()
{int n;cin >> n;euler(n);return 0;
}相关文章:

筛法求欧拉函数
思路: (1)若要分别求1~n每个数的欧拉函数值,则复杂度O(n*n^0.5),超时; (2)于是考虑用欧拉筛进行求取; (3)欧拉筛:基于线…...

consul限制注册的ip
假设当前服务器的ip是:192.168.56.130 1、允许 所有ip 注册(验证可行) consul agent -server -ui -bootstrap-expect1 -data-dir/usr/local/consul -nodedevmaster -advertise192.168.56.130 -bind0.0.0.0 -client0.0.0.0 2、只允许 当前ip 注册 consul agent -…...
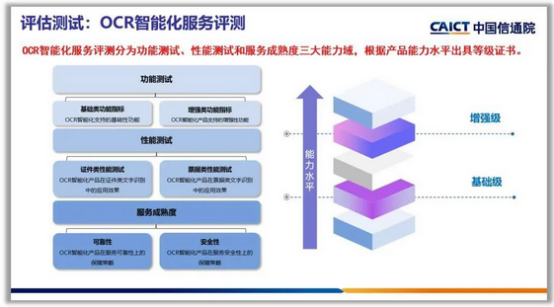
用AI攻克“智能文字识别创新赛题”,这场大学生竞赛掀起了什么风潮?
文章目录 一、前言1.1 大赛介绍1.2 项目背景 二、基于智能文字场景个人财务管理创新应用2.1 作品方向2.2 票据识别模型2.2.1 文本卷积神经网络TextCNN2.2.2 Bert 预训练微调2.2.3 模型对比2.2.4 效果展示 2.3 票据文字识别接口 三、未来展望 一、前言 1.1 大赛介绍 中国大学生…...

EJB基本概念和使用
一、EJB是什么? EJB是sun的JavaEE服务器端组件模型,是一种规范,设计目标与核心应用是部署分布式应用程序。EJB2.0过于复杂,EJB3.0的推出减轻了开发人员进行底层开发的工作量,它取消或最小化了很多(以前这些是必须实现)…...

神经网络基础-神经网络补充概念-09-m个样本的梯度下降
概念 当应用梯度下降算法到具有 m 个训练样本的逻辑回归问题时,我们需要对每个样本计算梯度并进行平均,从而更新模型参数。这个过程通常称为批量梯度下降(Batch Gradient Descent)。 代码实现 import numpy as npdef sigmoid(z…...
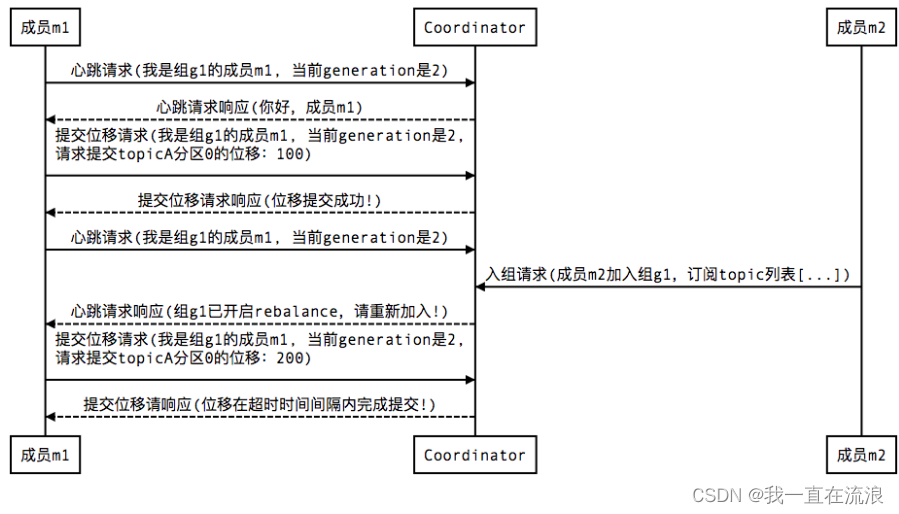
分布式 - 消息队列Kafka:Kafka消费者分区再均衡(Rebalance)
文章目录 01. Kafka 消费者分区再均衡是什么?02. Kafka 消费者分区再均衡的触发条件?03. Kafka 消费者分区再均衡的过程?04. Kafka 如何判定消费者已经死亡?05. Kafka 如何避免消费者的分区再均衡?06. Kafka 消费者分区再均衡有什…...
BIO、NIO和AIO
一.引言 何为IO 涉及计算机核心(CPU和内存)与其他设备间数据迁移的过程,就是I/O。数据输入到计算机内存的过程即输入,反之输出到外部存储(比如数据库,文件,远程主机)的过程即输出。 I/O 描述了计算机系统…...
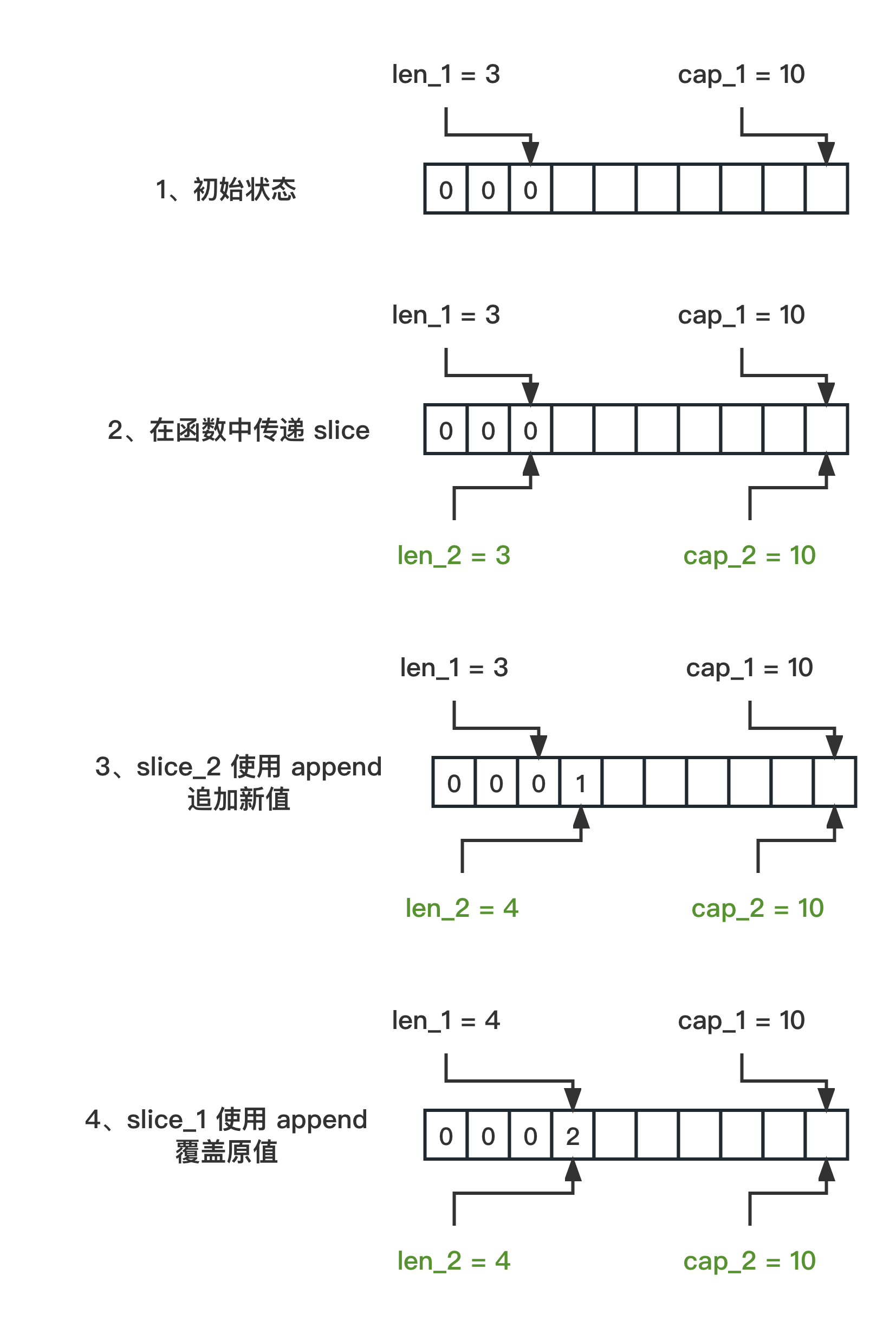
理解 Go 中的切片:append 操作的深入分析(篇1)
理解 Go 语言中 slice 的性质对于编程非常有益。下面,我将通过两个代码示例来解释切片在不同函数之间传递并执行 append 操作时的具体表现。 本篇为第 1 篇,当切片的容量 cap 充足时 第一份代码 slice1 的初始长度为 3,容量为 10 func main()…...
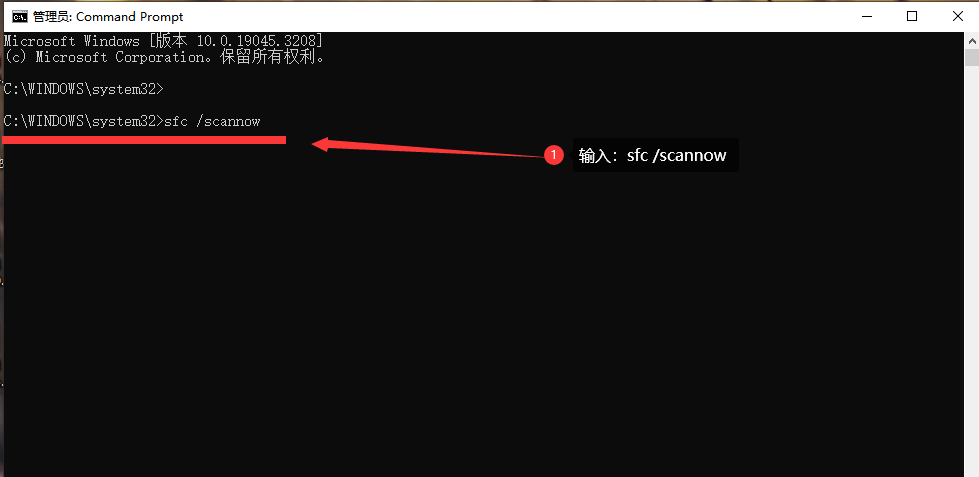
由于找不到mfc140u.dll,无法继续执行代码怎么修复?
当我在使用某个应用程序时遇到了mfc140u.dll缺失的错误提示时,我意识到这是由于该动态链接库文件丢失或损坏所引起的。mfc140u.dll是MFC的一部分,它包含了许多与用户界面、窗口管理、控件等相关的函数和类。这个文件通常用于支持使用MFC开发的应用程序的…...

【0.1】lubancat鲁班猫4刷入debian网络ping 域名不通问题
目录 1. 环境2. 操作步骤 1. 环境 lubancat4鲁班猫4 (4G0)不带emmc系统镜像lubancat-rk3588-debian11-gnome-20230807_update.img官方资料地址https://doc.embedfire.com/products/link/zh/latest/linux/ebf_lubancat.html 2. 操作步骤 从官网给的百度网盘下载linux系统全部…...
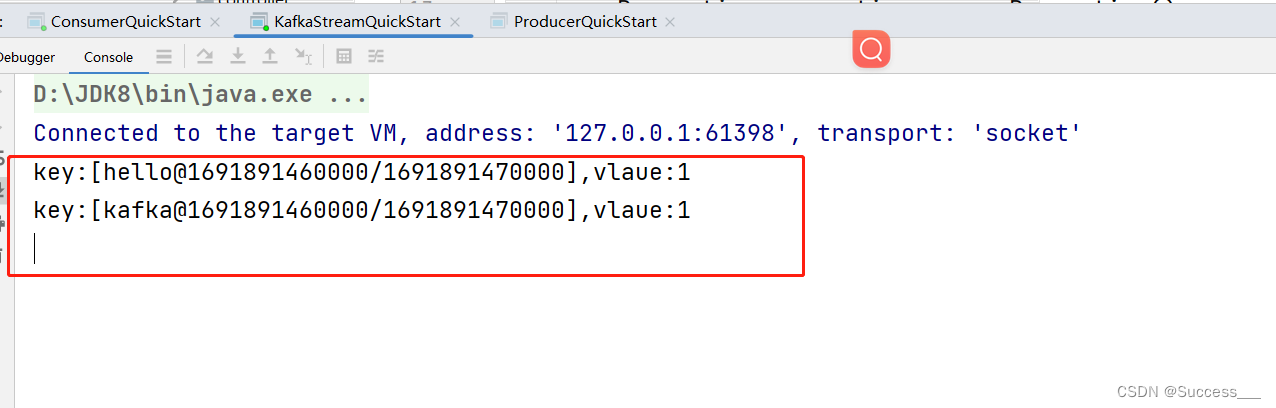
KafkaStream:基本使用
简介: kafkaStream:提供了对存储在kafka中的数据进行流式处理和分析的功能 特点: KafkasSream提供了一个非常简单轻量的Library,它可以非常方便的嵌入到java程序中,也可以任何方式打包部署 入门案例: 1、…...
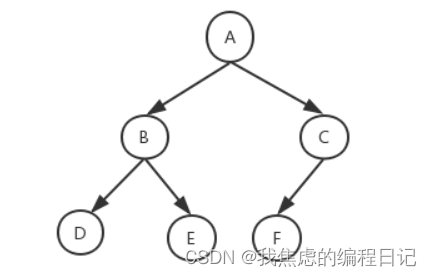
【数据结构】二叉树
完全二叉树 是指所有结点度数小于等于2的树 所以这种情况也是: 几条性质 一个具有n个结点的完全二叉树的深度为: log 2 ( n 1 ) 的结果向上取整。 \\\log_{2}(n1) \ \ 的结果向上取整。 log2(n1) 的结果向上取整。设度为0的结点个数是n0&#…...
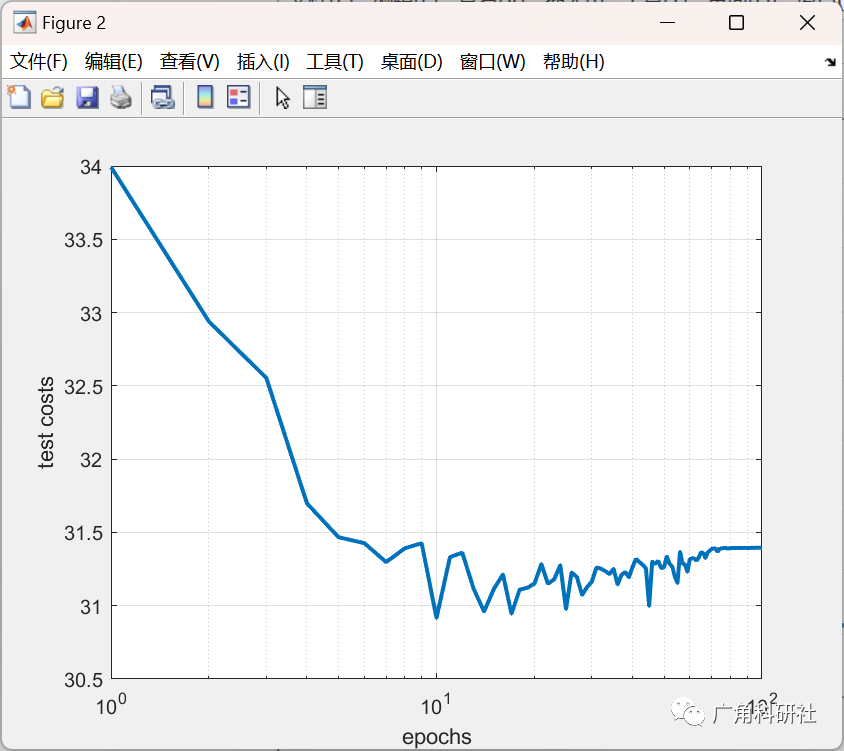
基于灰狼优化(GWO)、帝国竞争算法(ICA)和粒子群优化(PSO)对梯度下降法训练的神经网络的权值进行了改进(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
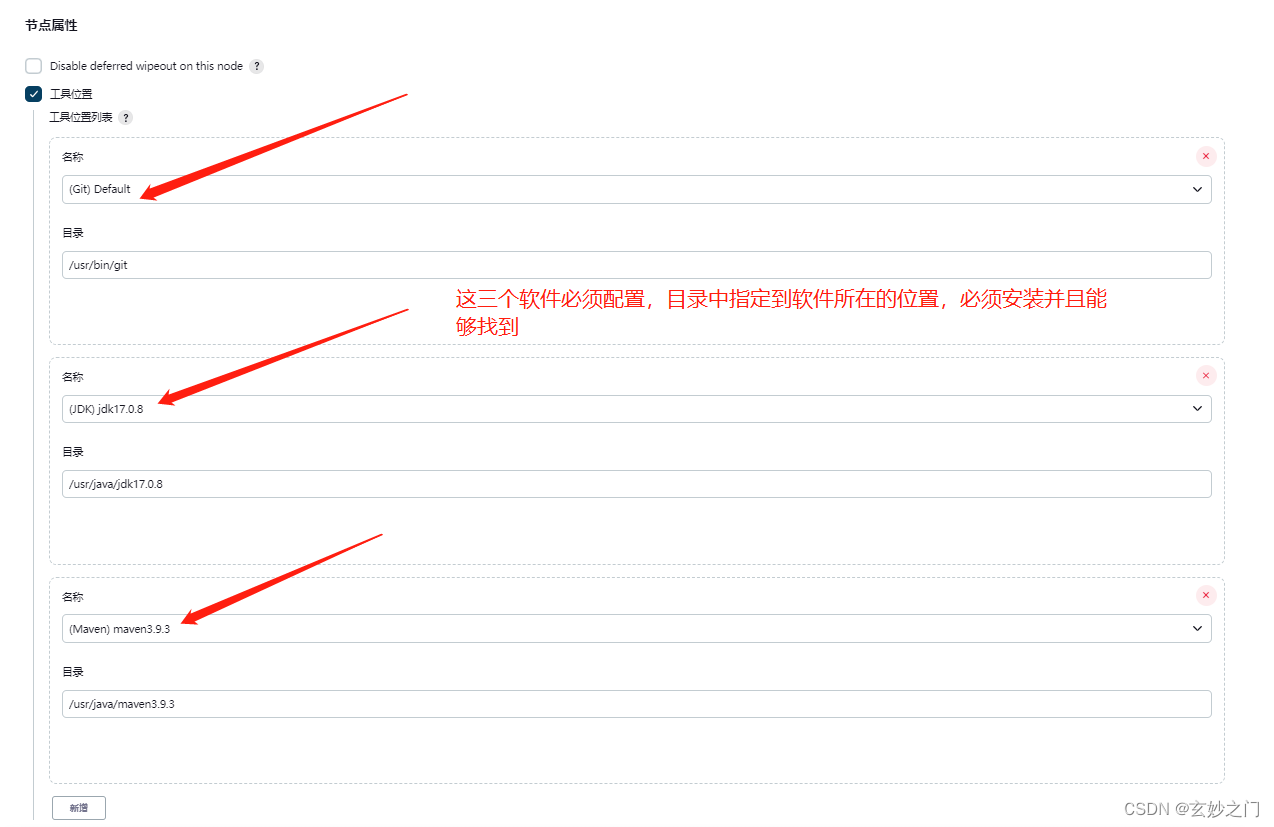
jenkins自动化构建保姆级教程(持续更新中)
1.安装 1.1版本说明 访问jenkins官网 https://www.jenkins.io/,进入到首页 点击【Download】按钮进入到jenkins下载界面 左侧显示的是最新的长期支持版本,右侧显示的是最新的可测试版本(可能不稳定),建议使用最新的…...

HTTPS 的加密流程
目录 一、HTTPS是什么? 二、为什么要加密 三、"加密" 是什么 四、HTTPS 的工作过程 1.对称加密 2.非对称加密 3.中间人攻击 4.证书 总结 一、HTTPS是什么? HTTPS (Hyper Text Transfer Protocol Secure) 是基于 HTTP 协议之上的安全协议&…...
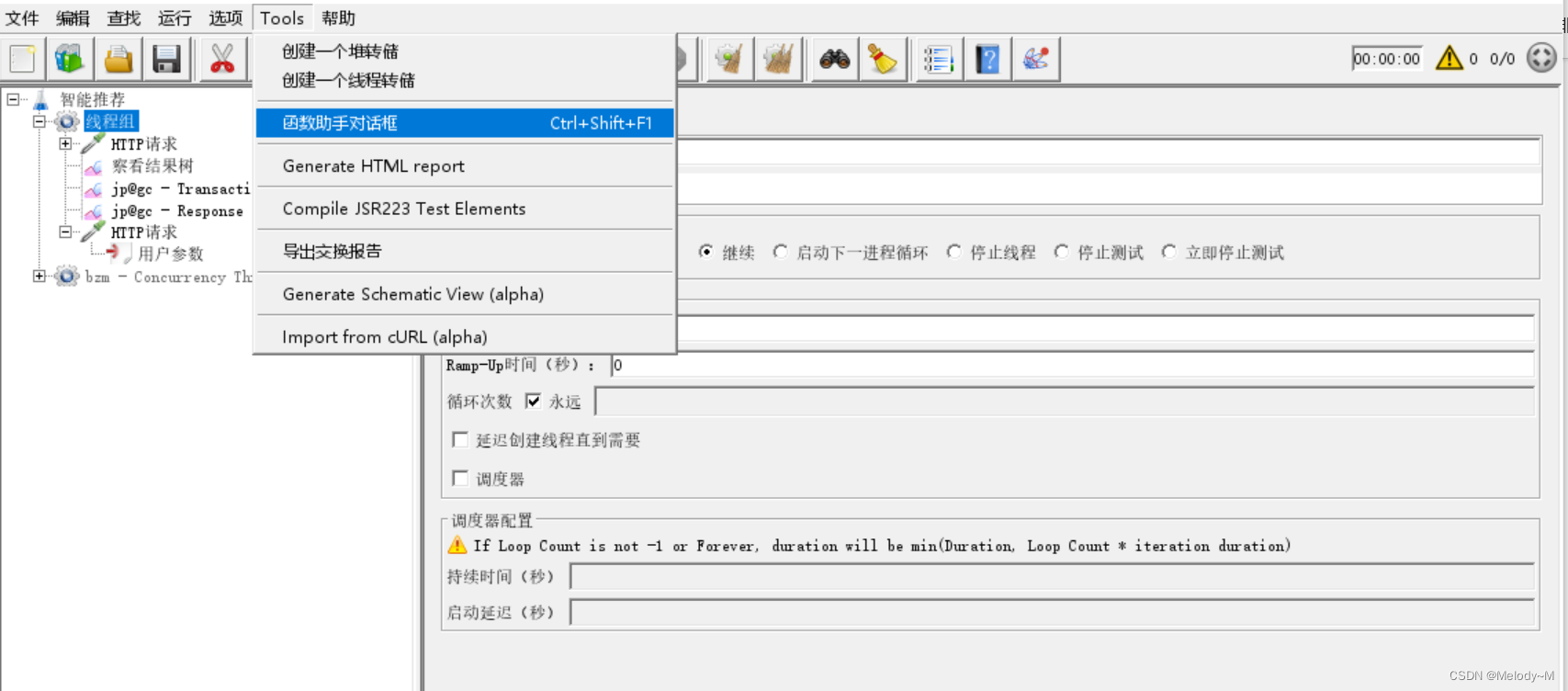
Jmeter 参数化的几种方法
目录 配置元件-用户自定义变量 前置处理器-用户参数 配置元件-CSV Data Set Config Tools-函数助手 配置元件-用户自定义变量 可在测试计划、线程组、HTTP请求下创建用户定义的变量 全局变量,可以跨线程组调用 jmeter执行的时候,只获取一次࿰…...

剑指Offer45.把数组排成最小的数 C++
1、题目描述 输入一个非负整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。 示例 1: 输入: [10,2] 输出: “102” 示例 2: 输入: [3,30,34,5,9] 输出: “3033459” 2、VS2019上运行 先转换成字符串再组合起来 #in…...
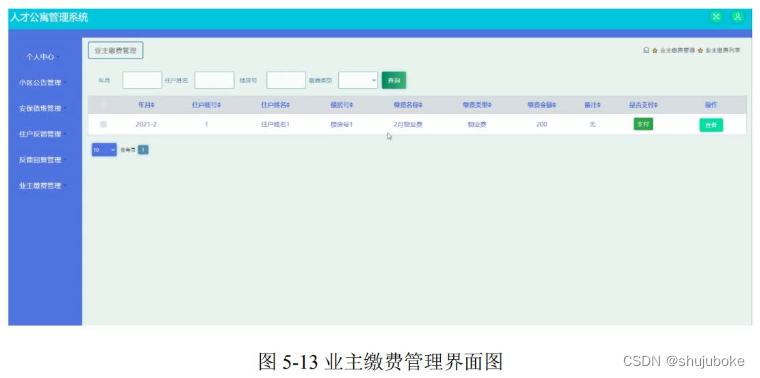
【java毕业设计】基于SSM+MySql的人才公寓管理系统设计与实现(程序源码)--人才公寓管理系统
基于SSMMySql的人才公寓管理系统设计与实现(程序源码毕业论文) 大家好,今天给大家介绍基于SSMMySql的人才公寓管理系统设计与实现,本论文只截取部分文章重点,文章末尾附有本毕业设计完整源码及论文的获取方式。更多毕业…...
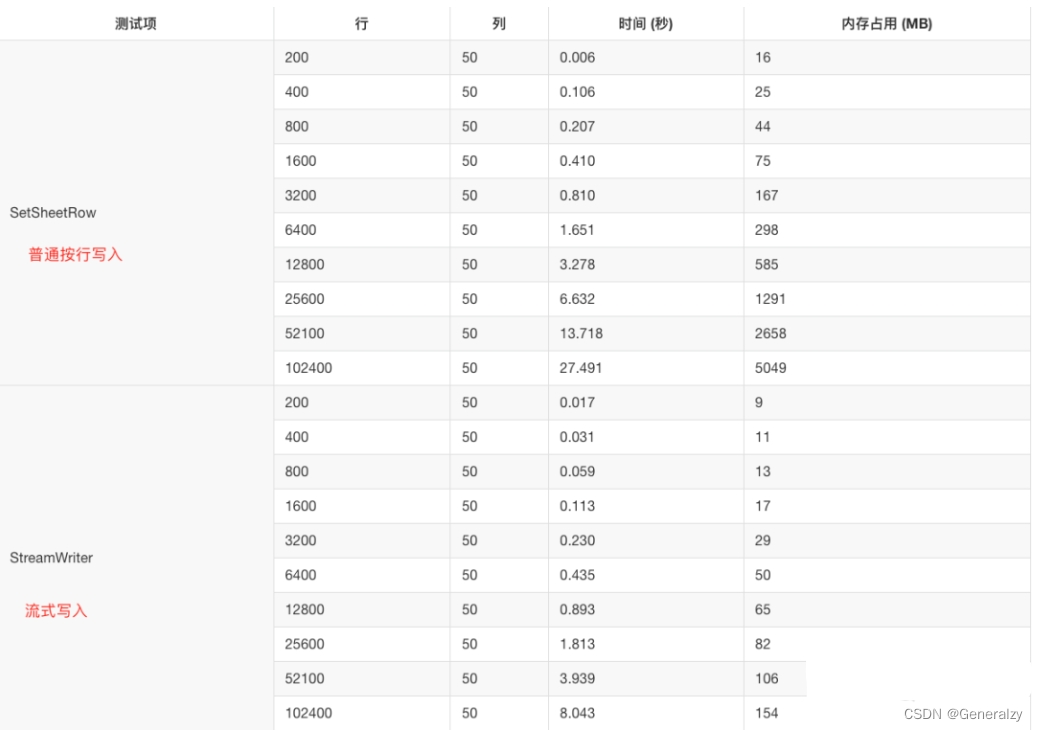
golang操作excel的高性能库——excelize/v2
目录 介绍文档与源码安装快速开始创建 Excel 文档读取 Excel 文档打开数据流流式写入 [相关 Excel 开源类库性能对比](https://xuri.me/excelize/zh-hans/performance.html) 介绍 Excelize是一个纯Go编写的库,提供了一组功能,允许你向XLAM / XLSM / XLS…...
学习51单片机怎么开始?
学习的过程不总是先打好基础,然后再盖上层建筑,尤其是实践性的、工程性很强的东西。如果你一定要先全面打好基础,再学习单片机,我觉得你一定学不好,因为你的基础永远打不好,因为基础太庞大了,基…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
