线段树(维护区间信息)
一,定义:
可以在logN时间内实现区间修改,单点修改,区间查询等操作的工具
二,思路(修改无乘法时):
1,建树
通过把区间不断二分建立一颗二叉树
我们以维护一个数组a={1,2,3,4,5}为例子
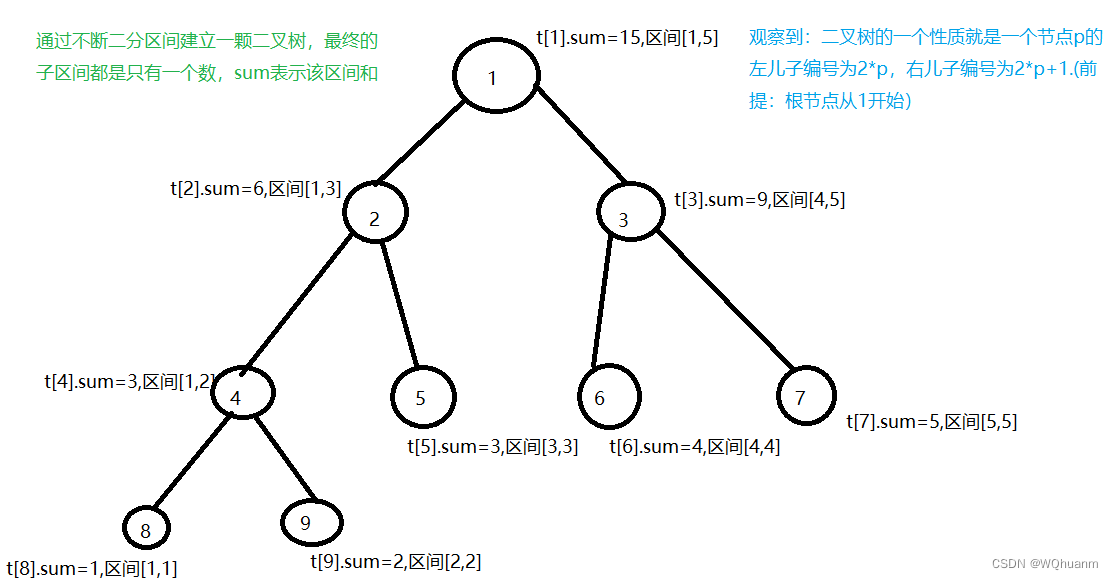
int a[N];
struct tree//我们以结构体来存储一颗树
{int l, r;//l,r表示该节点的区间ll sum, add;//sum表示区间和,add为懒惰标记
} t[N * 4 + 2]; //如果维护n个节点的区间,建立完整的二叉树大概需要4*n个树节点void build(int l, int r, int p)
{t[p].l = l, t[p].r = r; //首先存储节点p的区间if (l == r)//如果区间只有一个点{t[p].sum = a[l];//sum就是这个点的值return;}//否则继续二分遍历int mid = l + ((r - l) >> 1);// 移位运算符的优先级小于加减法,所以加上括号, // 如果写成 (l + r) >> 1 可能会超出 int 范围build(l, mid, 2 * p);build(mid + 1, r, 2 * p + 1);t[p].sum = t[2 * p].sum + t[2 * p + 1].sum;//回来后区间和就等于儿子们的区间和之和
}2,区间修改与懒惰标记
我们思考,如果我们给区间[2,5]都加上3,后面查询的时候只查询过[3,5]。那么请问,我们有没有必要花时间去更新[2,2]有加上3这件事呢。
显然没有必要,所以我们想要偷懒,我可以对你的修改标记一下,只有到我需要用到你时,才去修改他。
方法就是当我们更新一个区间时,我们就对这个区间进行标记(记录其修改的记录),如果后面我们要访问他的子代,我们首先先询问是否这个区间有标记,有则先更新他的子代,才可以去访问子代。
有了懒惰标记,我们每次深入只要深入到当前区间是目标区间子集就可以不用深入了,然后留下懒惰标记即可
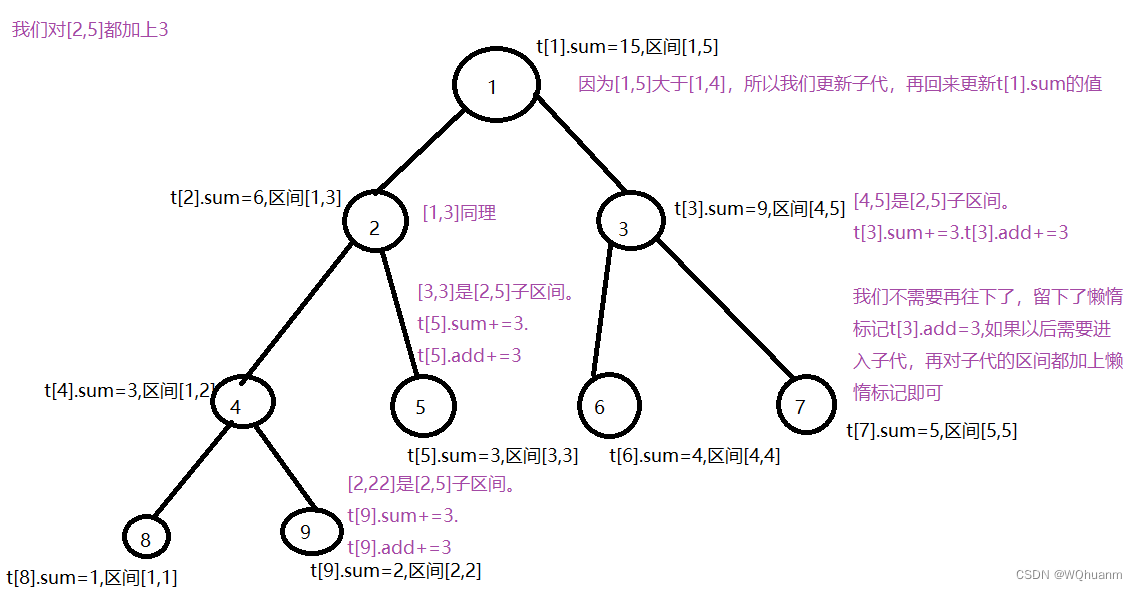
void lazy(int p)
{if (t[p].l == t[p].r)t[p].add = 0;//如果该区间只有一个点,毫无疑问他没有儿子,直接删除他的懒惰标记if (t[p].add)//如果懒惰区间不为0,更新儿子信息{//对儿子们的区间和更新t[2 * p].sum += t[p].add * (t[2 * p].r - t[2 * p].l + 1);t[2 * p + 1].sum += t[p].add * (t[2 * p + 1].r - t[2 * p + 1].l + 1);//每次更新区间就更新这个区间的懒惰标记,这样儿子访问子代时其懒惰区间才可以正常使用t[2 * p].add += t[p].add;t[2 * p + 1].add += t[p].add;//最后重置p的懒惰标记(他就是为子代存在的,而我们已经更新完子代了)t[p].add = 0;}
}void addupdate(int l, int r, int p, ll z)
{if (l <= t[p].l && t[p].r <= r)//如果当前p的区间是目标区间的子集,更新其区间值和懒惰标记就可以返回了{t[p].sum += z * (t[p].r - t[p].l + 1);t[p].add += z;return;}//如果不是全部属于目标区间,访问子代前先更新子代,清空自己的懒惰标记lazy(p);int mid = t[p].l + ((t[p].r - t[p].l) >> 1);if (l <= mid)addupdate(l, r, 2 * p, z);//如果[t[p].l,mid]有一部分属于目标区间,更新[l,mid]if (r > mid)addupdate(l, r, 2 * p + 1, z);//[mid+1,t[p].r]同理t[p].sum = t[2 * p].sum + t[2 * p + 1].sum;//回来后重新更新t[p].sum(因为子代已经更新)
}3,查询区间(单点值)
和修改的思考差不多,当前区间为目标区间子集就直接访问。否则就更新子代后深入子代
ll ask(int l, int r, int p)
{if (l <= t[p].l && t[p].r <= r)return t[p].sum;//属于子集直接返回lazy(p);//如果不是全部属于目标区间,访问子代前先更新子代,清空自己的懒惰标记int mid = t[p].l + ((t[p].r - t[p].l) >> 1);ll ans = 0;//ans累积属于目标区间的和if (l <= mid)ans += ask(l, r, 2 * p);if (r > mid)ans += ask(l, r, 2 * p + 1);return ans;
}三:模板题1:P3372 【模板】线段树 1
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define int ll
const int N = 1e5 + 10;int a[N];
struct tree//我们以结构体来存储一颗树
{int l, r;//l,r表示该节点的区间ll sum, add;//sum表示区间和,add为懒惰标记
} t[N * 4 + 2]; //如果维护n个节点的区间,建立完整的二叉树大概需要4*n个树节点void build(int l, int r, int p)
{t[p].l = l, t[p].r = r; //首先存储节点p的区间if (l == r)//如果区间只有一个点{t[p].sum = a[l];//sum就是这个点的值return;}//否则继续二分遍历int mid = l + ((r - l) >> 1);// 移位运算符的优先级小于加减法,所以加上括号, // 如果写成 (l + r) >> 1 可能会超出 int 范围build(l, mid, 2 * p);build(mid + 1, r, 2 * p + 1);t[p].sum = t[2 * p].sum + t[2 * p + 1].sum;//回来后区间和就等于儿子们的区间和之和
}void lazy(int p)
{if (t[p].l == t[p].r)t[p].add = 0;//如果该区间只有一个点,毫无疑问他没有儿子,直接删除他的懒惰标记if (t[p].add)//如果懒惰区间不为0,更新儿子信息{//对儿子们的区间和更新t[2 * p].sum += t[p].add * (t[2 * p].r - t[2 * p].l + 1);t[2 * p + 1].sum += t[p].add * (t[2 * p + 1].r - t[2 * p + 1].l + 1);//每次更新区间就更新这个区间的懒惰标记,这样儿子访问子代时其懒惰区间才可以正常使用t[2 * p].add += t[p].add;t[2 * p + 1].add += t[p].add;//最后重置p的懒惰标记(他就是为子代存在的,而我们已经更新完子代了)t[p].add = 0;}
}void addupdate(int l, int r, int p, ll z)
{if (l <= t[p].l && t[p].r <= r)//如果当前p的区间是目标区间的子集,更新其区间值和懒惰标记就可以返回了{t[p].sum += z * (t[p].r - t[p].l + 1);t[p].add += z;return;}//如果不是全部属于目标区间,访问子代前先更新子代,清空自己的懒惰标记lazy(p);int mid = t[p].l + ((t[p].r - t[p].l) >> 1);if (l <= mid)addupdate(l, r, 2 * p, z);//如果[t[p].l,mid]有一部分属于目标区间,更新[l,mid]if (r > mid)addupdate(l, r, 2 * p + 1, z);//[mid+1,t[p].r]同理t[p].sum = t[2 * p].sum + t[2 * p + 1].sum;//回来后重新更新t[p].sum(因为子代已经更新)
}ll ask(int l, int r, int p)
{if (l <= t[p].l && t[p].r <= r)return t[p].sum;//属于子集直接返回lazy(p);//如果不是全部属于目标区间,访问子代前先更新子代,清空自己的懒惰标记int mid = t[p].l + ((t[p].r - t[p].l) >> 1);ll ans = 0;//ans累积属于目标区间的和if (l <= mid)ans += ask(l, r, 2 * p);if (r > mid)ans += ask(l, r, 2 * p + 1);return ans;
}int32_t main()
{std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int n, m;cin >> n >> m;for (int i = 1; i <= n; ++i)cin >> a[i];build(1, n, 1);//每次都从根节点p=1建树int b, l, r, k;while (m--){cin >> b >> l >> r;if (b == 1){cin >> k;addupdate(l, r, 1, k);//更新,查询也都成根节点p=1开始}else if (b == 2){cout << ask(l, r, 1) << endl;//更新,查询也都成根节点p=1开始}}return 0;
}四,思考(如果区间修改同时存在加法和乘法怎么办)
1,我们清楚,乘法就是把当前的区间都*一个值(当然,这个区间是更新过的,因为每次都是更新完这个区间才进入)。
2,我们考虑使用乘法的影响,当我们对当前p的区间乘z时,t[p].sum*=z,那么更新他的懒惰标记
,以子代2*p为例子,他的子代目前是(t[2p]*t[p].mul+t[p].add*size(2p)),我们*z<-->t[2p]*z*t[p].mul*z+t[p].add*z,所以我们一次要更新t[p].mul,t[p].add。
3,我们考虑进入子代前对懒惰标记的处理,我们发现,t[p].add是可以不断用加法与乘法叠加的,而mul一直都是被乘没有加(在进入这一层之前都是这样)。所以我们更新这一层,首先一定要先乘mul在加add。这对t[2*p].sum与t[2*p].add都是一样的,都是先*t[p].mul再加t[p].add
直接上模板题:P3373 【模板】线段树 2
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define int ll
typedef unsigned long long ull;
typedef pair<long long, long long> pll;
typedef pair<int, int> pii;//double 型memset最大127,最小128
//std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
const int INF = 0x3f3f3f3f; //int型的INF
const ll llINF = 0x3f3f3f3f3f3f3f3f;//ll型的llINF
const int N = 1e5 + 10;int a[N];
int n, m, mod;
struct tree
{int l, r;ll sum, add, mul;
} t[4 * N + 2];void build(int l, int r, int p)
{t[p].l = l, t[p].r = r, t[p].mul = 1; //这里多更新了一个mul的初始值是1if (l == r){t[p].sum = a[l] % mod;return;}int mid = l + ((r - l) >> 1);build(l, mid, 2 * p);build(mid + 1, r, 2 * p + 1);t[p].sum = (t[2 * p].sum + t[2 * p + 1].sum) % mod;
}void lazy(int p)
{if (t[p].l == t[p].r)t[p].add = 0, t[p].mul = 1;if (t[p].add || t[p].mul != 1)//只要加法或者乘法有一个存在懒惰标记就更新{t[2 * p].sum = (t[2 * p].sum * t[p].mul + t[p].add * (t[2 * p].r - t[2 * p].l + 1)) % mod;t[2 * p + 1].sum = (t[2 * p + 1].sum * t[p].mul + t[p].add * (t[2 * p + 1].r - t[2 * p + 1].l + 1)) % mod;//更新sum与add都是先乘后加t[2 * p].add = (t[2 * p].add * t[p].mul + t[p].add) % mod;t[2 * p + 1].add = (t[2 * p + 1].add * t[p].mul + t[p].add) % mod;t[2 * p].mul = (t[2 * p].mul * t[p].mul) % mod;t[2 * p + 1].mul = (t[2 * p + 1].mul * t[p].mul) % mod;//重置标记t[p].add = 0, t[p].mul = 1;}
}void addupdate(int l, int r, int p, ll z)
{if (l <= t[p].l && t[p].r <= r){t[p].sum = (t[p].sum + z * (t[p].r - t[p].l + 1)) % mod;t[p].add = (t[p].add + z) % mod;return;}lazy(p);int mid = t[p].l + ((t[p].r - t[p].l) >> 1);if (l <= mid)addupdate(l, r, 2 * p, z);//只有子代有在目标区间才进入if (r > mid)addupdate(l, r, 2 * p + 1, z);t[p].sum = (t[2 * p].sum + t[2 * p + 1].sum) % mod;
}void mulupdate(int l, int r, int p, ll z)
{if (l <= t[p].l && t[p].r <= r){t[p].sum = (t[p].sum * z) % mod;//乘法需要对p的sum,add,mul都更新t[p].add = (t[p].add * z) % mod;t[p].mul = (t[p].mul * z) % mod;return;}lazy(p);int mid = t[p].l + ((t[p].r - t[p].l) >> 1);if (l <= mid)mulupdate(l, r, 2 * p, z);//只有子代有在目标区间才进入if (r > mid)mulupdate(l, r, 2 * p + 1, z);t[p].sum = (t[2 * p].sum + t[2 * p + 1].sum) % mod;
}ll ask(int l, int r, int p)
{if (l <= t[p].l && t[p].r <= r)return t[p].sum % mod;lazy(p);int mid = t[p].l + ((t[p].r - t[p].l) >> 1);ll ans = 0;if (l <= mid)ans += ask(l, r, 2 * p);if (r > mid)ans += ask(l, r, 2 * p + 1);return ans % mod;
}int32_t main()
{cin >> n >> m >> mod;for (int i = 1; i <= n; ++i)cin >> a[i];build(1, n, 1);int b, l, r, k;while (m--){cin >> b >> l >> r;if (b == 1){cin >> k;mulupdate(l, r, 1, k);}else if (b == 2){cin >> k;addupdate(l, r, 1, k);}else if (b == 3){cout << ask(l, r, 1) << endl;}}return 0;
}
相关文章:

线段树(维护区间信息)
一,定义: 可以在logN时间内实现区间修改,单点修改,区间查询等操作的工具 二,思路(修改无乘法时): 1,建树 通过把区间不断二分建立一颗二叉树 我们以维护一个数组a{1…...
C语言 基于Ncurse库的贪吃蛇游戏项目
为了敲键盘及时响应,需要用到ncurse 测试代码: ncurse1.c /* ncurse1.c */ #include <curses.h> //ncurse的头文件。int main() {char c;int i 0;//ncurse界面的初始化函数。initscr(); for(i0;i<2;i){c getch();printw("\n");//…...
【Java基础】Java语言特性
认识Java java语言的执行过程 编写纯文本文件 .java 经过javac编译器(java complier)编译 .class .class是二进制的字节码 在源文件中定义几个类,就会生成几个 由JVM运行 .class JVM把字节码编译成可以在处理器上运行的高性能的本地代码(native code),…...
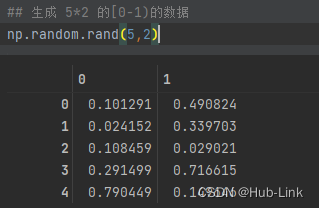
python进阶--Numyp库(一)
一、Numpy库介绍 NumPy(Numerical Python)是Python的⼀种开源的数值计算扩展。提供多维数组对象,各种派⽣对象(如掩码数组和矩阵),这种⼯具可⽤来存储和处理⼤型矩阵,⽐Python⾃身的嵌套列表&am…...

CV学习笔记-Inception
CV学习笔记-Inception 目录 文章目录CV学习笔记-Inception目录1. 常见的卷积神经网络2. Inception(1) Inception提出背景(2) Inception module 核心思想3. Inception的历史版本(1) InceptionV1-GoogleNet(2) InceptionV2(3) InceptionV3(4) Inception V44. Inception模型的特点…...
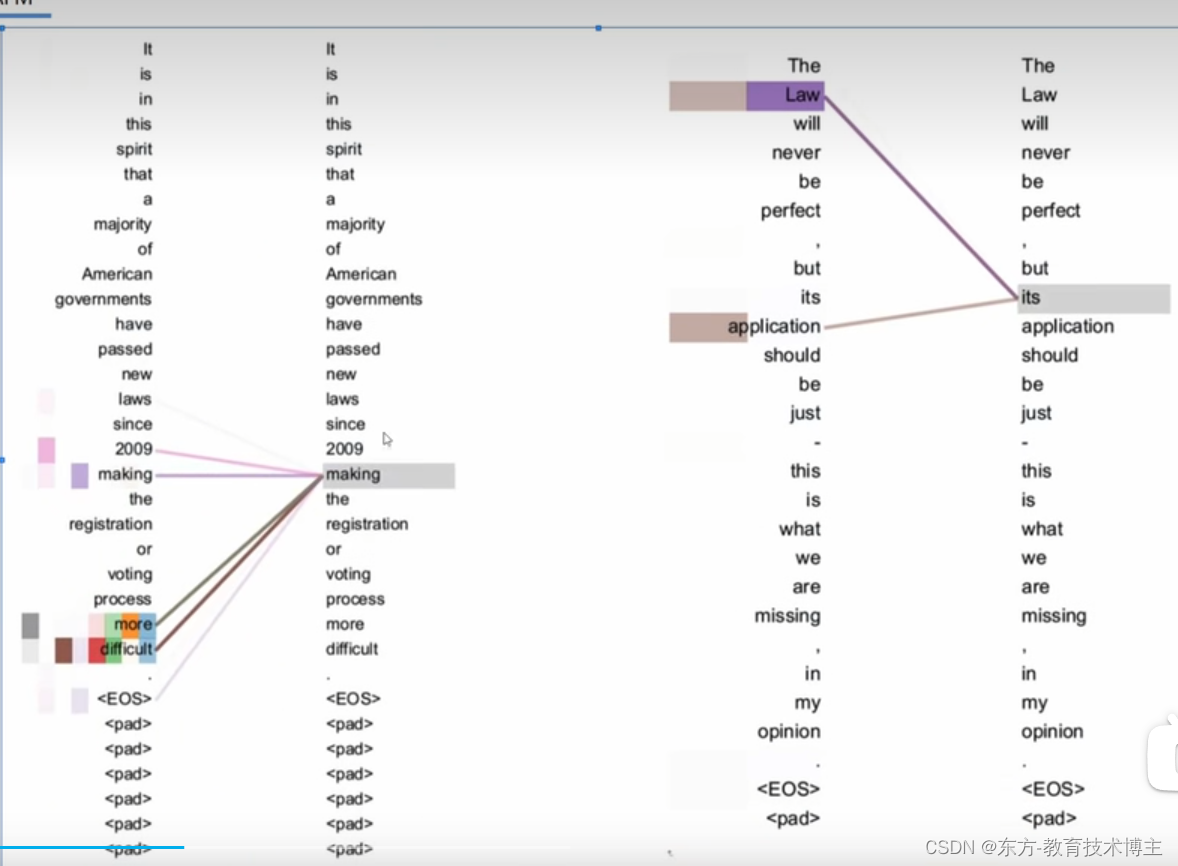
注意力机制笔记——结合沐神和B站老弓up主
B站【大白话浅谈【注意力机制】】 聚类 是针对 样本, 注意力机制是针对样本相关性,来进行计算的 自注意力机制 指的是 query ,key,value都是同一个部分。 可以学到 类似的 短语 ,和 语义特征。如its 指代的对象。 评论区大佬 根据这篇论文《Effective Approaches to…...
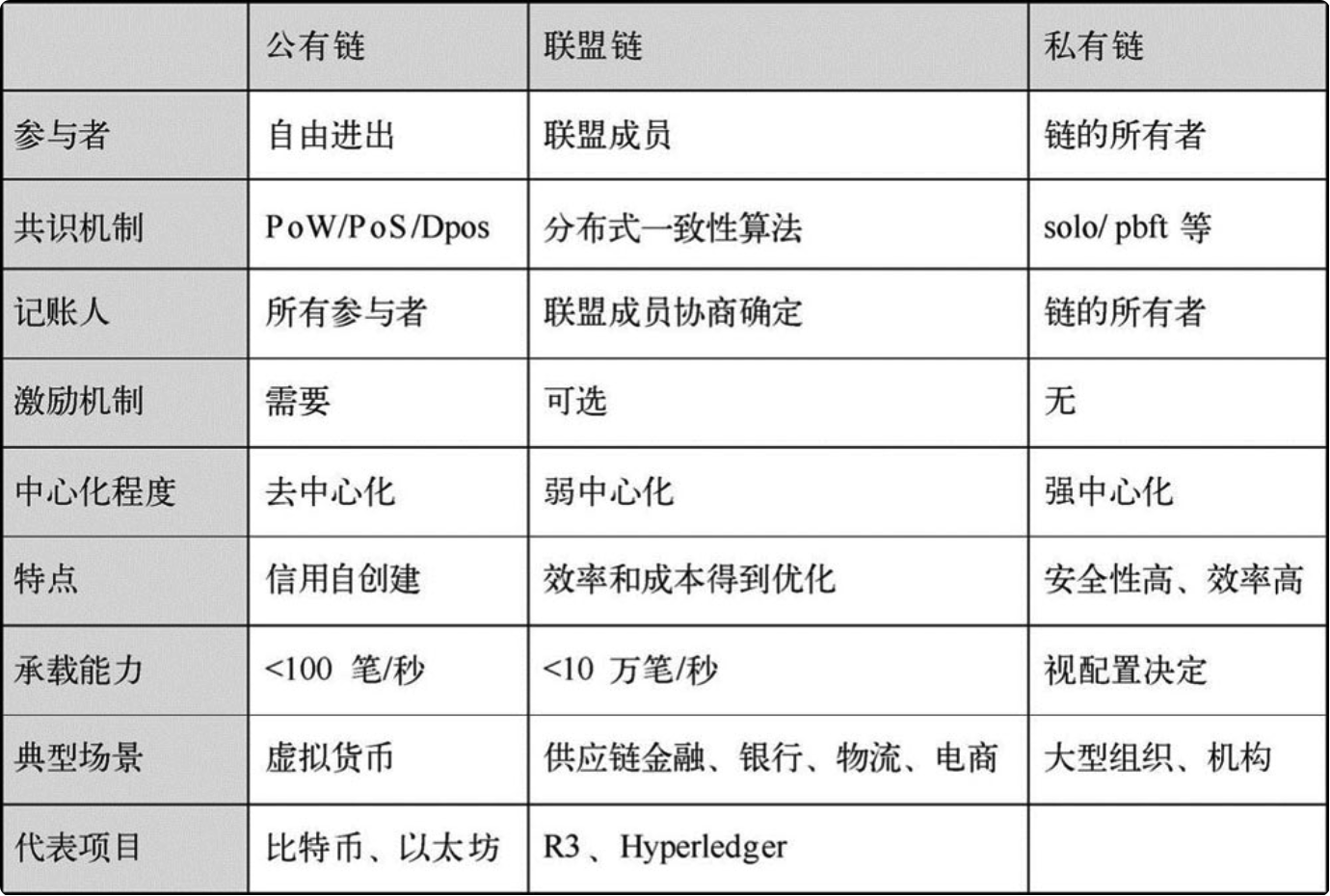
建议收藏,轻松搞懂区块链
未来已来,只是不均衡地分布在当下 大家好,我是菜农,欢迎来到我的频道。 本文共 5844字,预计阅读 30 分钟 区块链是近些年来最热门的前沿技术,被认为是未来十几年对金融、物联网、医疗等诸多领域产生最大影响的"…...

php设计一个新春祝福墙
记得十几年前的时候,每到春节,各大网站都会建一个祝福墙,上面挂满网友的新年寄语。这些年随着移动互联网的高速发展,web的新春祝福墙越来越少了。今天,咱们就来考考古,用快速原型法进行设计。原型设计采用M…...

KubeSphere 社区双周报 | OpenFunction 集成 WasmEdge | 2023.02.03-02.16
KubeSphere 社区双周报主要整理展示新增的贡献者名单和证书、新增的讲师证书以及两周内提交过 commit 的贡献者,并对近期重要的 PR 进行解析,同时还包含了线上/线下活动和布道推广等一系列社区动态。 本次双周报涵盖时间为:2023.02.03-2023.…...

数字IC/FPGA 秋招知识点不全面整理
1. 引言 这篇文章的由来 秋招的时候,刚开始复习一些知识点的时候没有什么思路,只是盲目的看相关的书籍和资料,结果是留在脑子中的知识很有限,而且不够系统,在我需要它的时候,并不能很快的回忆起来。 于是就想着把一些典型的知识整理成一个文档,在进行刷题的时候可以比…...

你知道java8是如何排序Map嘛?
在Java中,有多种方法可以对Map进行排序,但是我们将重点介绍Java 8 Stream,这是实现目标的一种非常优雅的方法。 学习一下HashMap的merge()函数 在学习Map排序之前,有必要讲一下HashMap的merge()函数,该函数应用场景就…...

【李忍考研传】一、李忍
“老师,我来回答!” “非常好,我记得你是叫……呃……是李念同学吗?” “不,老师,我叫李忍。” “好,你来回答一下这个问题。” “这题用海明码校验的知识,能检错一位纠错一位&a…...

测牛学堂:软件测试python深入之类和对象的属性和方法总结
类对象和实例对象 类对象就是我们定义的类。 在代码执行的时候,解释器会自动创建类对象。 类对象的作用: 1 使用类对象创建实例对象 2 存储类的一些特性,就是类里面定义的属性 创建对象的过程也称为实例化的对象。所以,类创建的对…...

css实例--新闻页面
实现效果 实现代码 html代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" co…...

SpringCloudGateway 动态转发后端服务
API网关的核心功能是统一流量入口,实现路由转发,SpringCloudGateway是API网关开发的技术之一,此外比较流行的还有Kong和ApiSix,这2个都是基于OpenResty技术栈。 简单的路由转发可以通过SpringCloudGateway的配置文件实现…...

使用canvas写一个flappy bird小游戏
简介 canvas 是HTML5 提供的一种新标签,它可以支持 JavaScript 在上面绘画,控制每一个像素,它经常被用来制作小游戏,接下来我将用它来模仿制作一款叫flappy bird的小游戏。flappy bird(中文名:笨鸟先飞&am…...

KVM-2、虚拟化基础
1. 虚拟化概念 什么是虚拟化 **虚拟化是使用所谓虚拟机管理程序从一台物理机上创建若干个虚拟机的过程。**虚拟机的行为和运转方式与物理机一样,但它们会使用物理机的计算资源,如 CPU 、内存和存储。虚拟机管理程序会根据需要将这些计算资源分配给每个虚拟机。 虚拟化有哪…...
设计模式之观察者模式与访问者模式详解和应用
目录1.访问者模式详解1.1 访问者模式的定义1.1.1 访问者模式在生活中的体现1.1.2 访问者模式的适用场景1.2 访问者模式的通用实现1.3 访问者模式的使用案例之KPI考核1.3.1 类图设计1.3.2 代码实现1.4 访问者模式扩展---分派1.4.1 java中静态分派示例代码1.4.2 java中动态分派1.…...
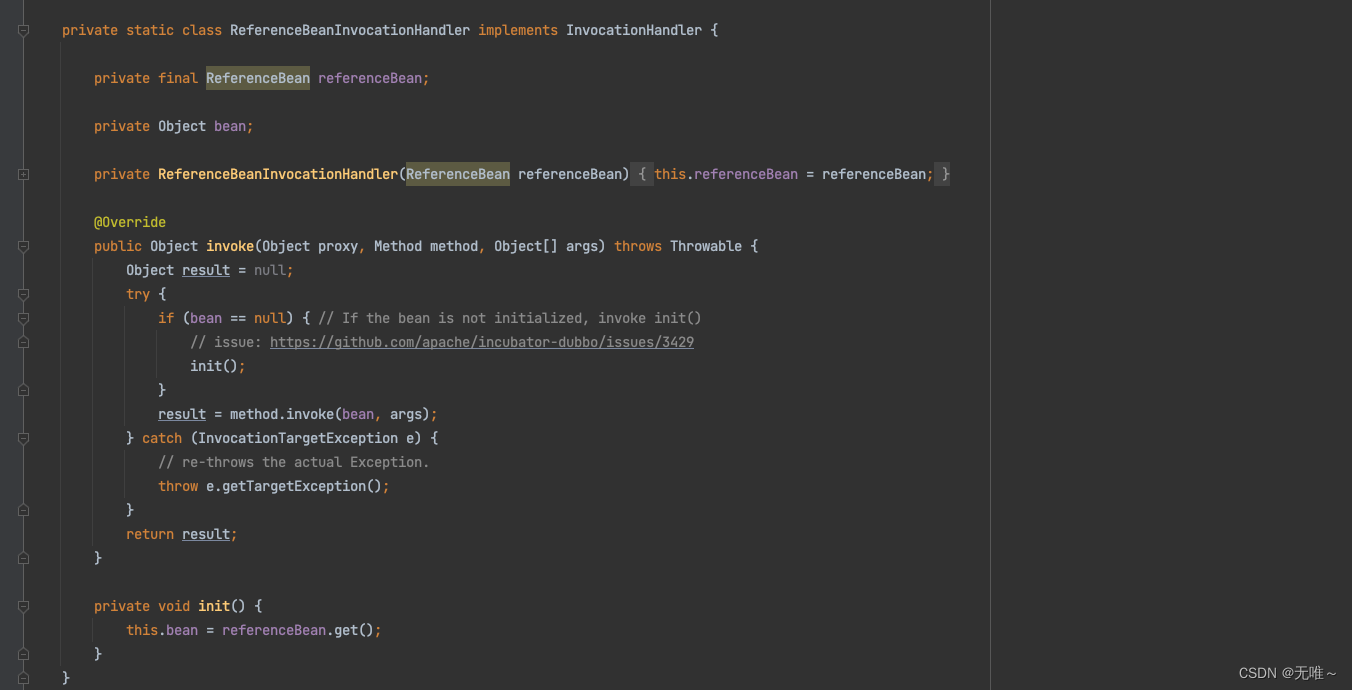
spring注解方式整合Dubbo源码解析
系列文章目录 前言 本节我们的Dubbo源码版本基于2.6.x 在前一章我们的整合案例中,我们有几个比较关键的步骤: 在启动类上标注了EnableDubbo注解在provider类上面标注了Service注解来提供dubbo服务在消费的时候通过Reference注解引入dubbo服务在配置文件…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

