P1009 阶乘之和
[NOIP1998 普及组] 阶乘之和
题目描述
用高精度计算出 S = 1 ! + 2 ! + 3 ! + ⋯ + n ! S = 1! + 2! + 3! + \cdots + n! S=1!+2!+3!+⋯+n!( n ≤ 50 n \le 50 n≤50)。
其中 ! 表示阶乘,定义为 n ! = n × ( n − 1 ) × ( n − 2 ) × ⋯ × 1 n!=n\times (n-1)\times (n-2)\times \cdots \times 1 n!=n×(n−1)×(n−2)×⋯×1。例如, 5 ! = 5 × 4 × 3 × 2 × 1 = 120 5! = 5 \times 4 \times 3 \times 2 \times 1=120 5!=5×4×3×2×1=120。
输入格式
一个正整数 n n n。
输出格式
一个正整数 S S S,表示计算结果。
样例 #1
样例输入 #1
3
样例输出 #1
9
提示
【数据范围】
对于 100 % 100 \% 100% 的数据, 1 ≤ n ≤ 50 1 \le n \le 50 1≤n≤50。
【其他说明】
注,《深入浅出基础篇》中使用本题作为例题,但是其数据范围只有 n ≤ 20 n \le 20 n≤20,使用书中的代码无法通过本题。
如果希望通过本题,请继续学习第八章高精度的知识。
#include<bits/stdc++.h>
using namespace std;
int n,a[101]={0},s[101]={0};
void change(int x)
{int g=0;for(int i=100;i>=0;i--){a[i]=a[i]*x+g;g=a[i]/10;a[i]=a[i]%10;}
}
void sum()
{int g=0;for(int i=100;i>=0;i--){s[i]=s[i]+a[i]+g;g=s[i]/10;s[i]=s[i]%10;}
}
void mul()
{int w;for(int i=0;i<=100;i++){if(s[i]!=0){w=i;break;}}for(int i=w;i<=100;i++)printf("%d",s[i]);
}
int main()
{scanf("%d",&n);s[100]=a[100]=1;for(int i=2;i<=n;i++){change(i);sum();}mul();return 0;
}
ps:
本体高精乘法
相关文章:

P1009 阶乘之和
[NOIP1998 普及组] 阶乘之和 题目描述 用高精度计算出 S 1 ! 2 ! 3 ! ⋯ n ! S 1! 2! 3! \cdots n! S1!2!3!⋯n!( n ≤ 50 n \le 50 n≤50)。 其中 ! 表示阶乘,定义为 n ! n ( n − 1 ) ( n − 2 ) ⋯ 1 n!n\times (n-1)…...
)
Linux内核源码剖析之TCP保活机制(KeepAlive)
写在前面: 版本信息: Linux内核2.6.24(大部分centos、ubuntu应该都在3.1。但是2.6的版本比较稳定,后续版本本质变化也不是很大) ipv4 协议 https://blog.csdn.net/ComplexMaze/article/details/124201088 本文使用案例…...

后端 springboot 给 vue 提供参数
前端 /** 发起新增或修改的请求 */requestAddOrEdit(formData) {debuggerif(formData.id undefined) {formData.id }getAction(/material/getNameModelStandard, {standard: this.model.standard,name: this.model.name,model: this.model.model}).then((res) > {if (res …...

《vue3实战》运用radio单选按钮或Checkbox复选框实现单选多选的试卷制作
文章目录 目录 系列文章目录 1.《Vue3实战》使用axios获取文件数据以及走马灯Element plus的运用 2.《Vue3实战》用路由实现跳转登录、退出登录以及路由全局守护 3.《vue3实战》运用Checkbox复选框实现单选多选的试卷展现(本文) 文章目录 前言 radio是什…...

排序算法-冒泡排序(C语言实现)
简介😀 冒泡排序是一种简单但效率较低的排序算法。它重复地扫描待排序元素列表,比较相邻的两个元素,并将顺序错误的元素交换位置,直到整个列表排序完成。 实现🧐 以下内容为本人原创,经过自己整理得出&am…...
星际争霸之小霸王之小蜜蜂(一)
目录 前言 一、安装pygame库 1、pygame库简介 2、在windows系统安装pygame库 二 、搭建游戏框架 1、创建游戏窗口 2、改变窗口颜色 总结 前言 大家应该都看过或者都听说过python神书“大蟒蛇”,上面有一个案例是《外星人入侵》,游戏介绍让我想起了上…...

图数据库_Neo4j基于docker服务版安装_Neo4j Desktop桌面版安装---Neo4j图数据库工作笔记0004
然后我们来看看如何用docker来安装Neo4j community server 首先去执行docker pull neo4j:3.5.22-community 去拉取镜像 然后执行命令就可以安装了 可以用docker ps查看一下 看看暴露了哪些端口 然后再看一下访问一下这个时候,要用IP地址了注意 然后再来看一下安装Desktop 去下…...

docker-compose部署可道云
文章目录 一. Mac1.1 下载源码1.2 部署1.2.1 修改密码部署(可忽略)1.2.2 直接部署 1.3 卸载1.4 访问 二. Win2.1 下载源码2.2 部署2.2.1 修改密码部署(可忽略)2.2.2 直接部署 2.3 卸载 一. Mac 1.1 下载源码 mkdir -p /Users/wanfei/docker-compose && cd /Users/wan…...

Windows上使用FFmpeg实现本地视频推送模拟海康协议rtsp视频流
场景 Nginx搭建RTMP服务器FFmpeg实现海康威视摄像头预览: Nginx搭建RTMP服务器FFmpeg实现海康威视摄像头预览_nginx rtmp 海康摄像头_霸道流氓气质的博客-CSDN博客 上面记录的是使用FFmpeg拉取海康协议摄像头的rtsp流并推流到流媒体服务器。 如果在其它业务场景…...

单片机之从C语言基础到专家编程 - 4 C语言基础 - 4.8 运算符
1.算术运算符 运算符名称备注加法运算符双目运算,a b-减法运算符双目运算,a - b*乘法运算符双目运算,a * b/除法运算符双目运算,a / b%求余运算符双目运算, a % b自增运算符单目运算, a–自减运算符单目运算, a– 2.关系运算符…...
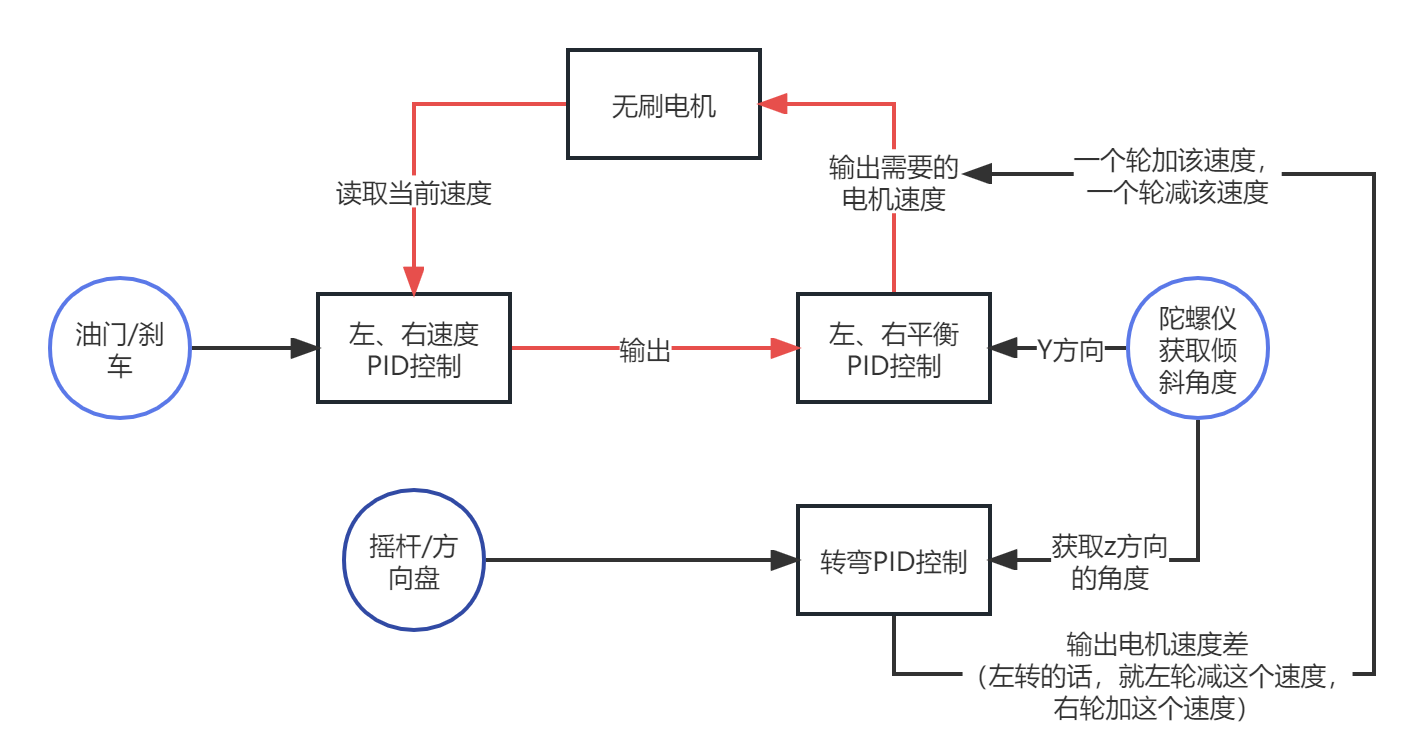
轮腿机器人的PID控制
1 PID介绍 PID(Proportional Integral Derivative)控制系统。其实质是根据输入的偏差值,按比例、积分、微分的函数关系进行运算,运算结果用以输出进行控制。它是在长期的工程实践中总结出来的一套控制方法,实际运行经…...

ChatGPT爆火,会给教育带来什么样的影响或者冲击?
近来,人工智能聊天机器人ChatGPT连上热搜,火爆全网。ChatGPT拥有强大的信息整合能力、自然语言处理能力,可谓是“上知天文,下知地理”,而且还能根据要求进行聊天、撰写文章等。 ChatGPT一经推出,便迅速在社…...

Servlet+JDBC实战开发书店项目讲解第三篇:商品查询实现
ServletJDBC实战开发书店项目讲解第三篇:商品查询实现 本篇博客将介绍如何在ServletJDBC实战开发书店项目中实现商品查询功能。我们将从设计数据库表结构和实体类开始,一步一步详细讲解代码实现过程,包括前端页面的设计和后端Servlet代码的编…...
爬虫逆向实战(十七)--某某丁简历登录
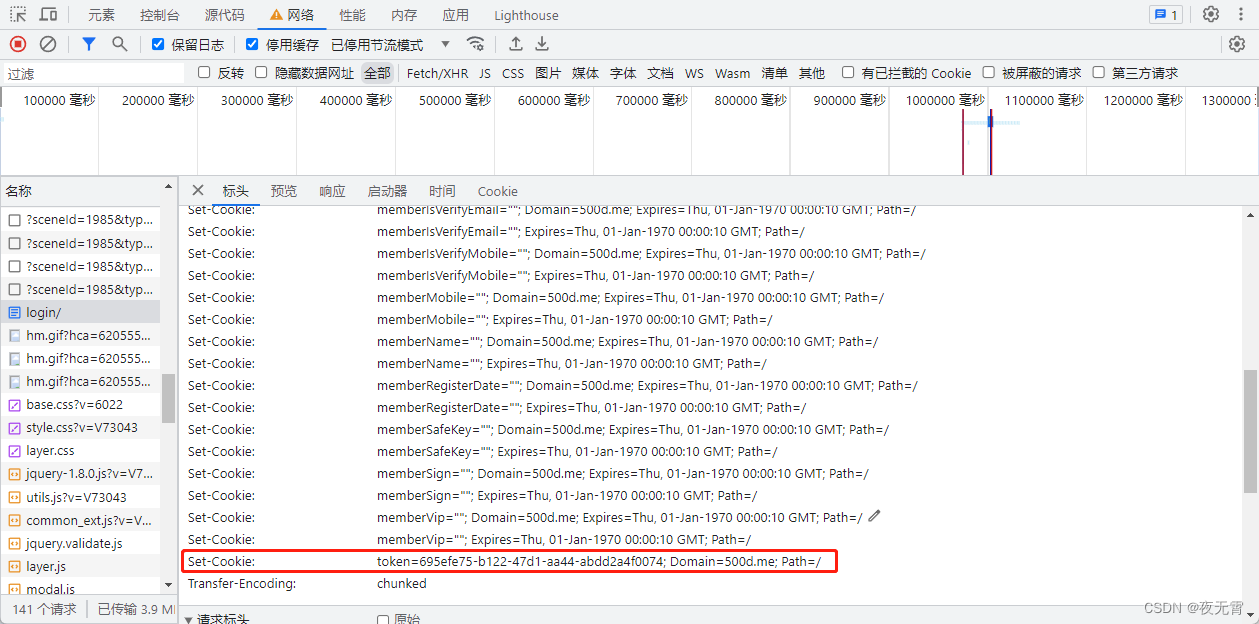
一、数据接口分析 主页地址:某某丁简历 1、抓包 通过抓包可以发现数据接口是submit 2、判断是否有加密参数 请求参数是否加密? 通过查看“载荷”模块可以发现有一个enPassword加密参数 请求头是否加密? 通过查看请求头可以发现有一个To…...
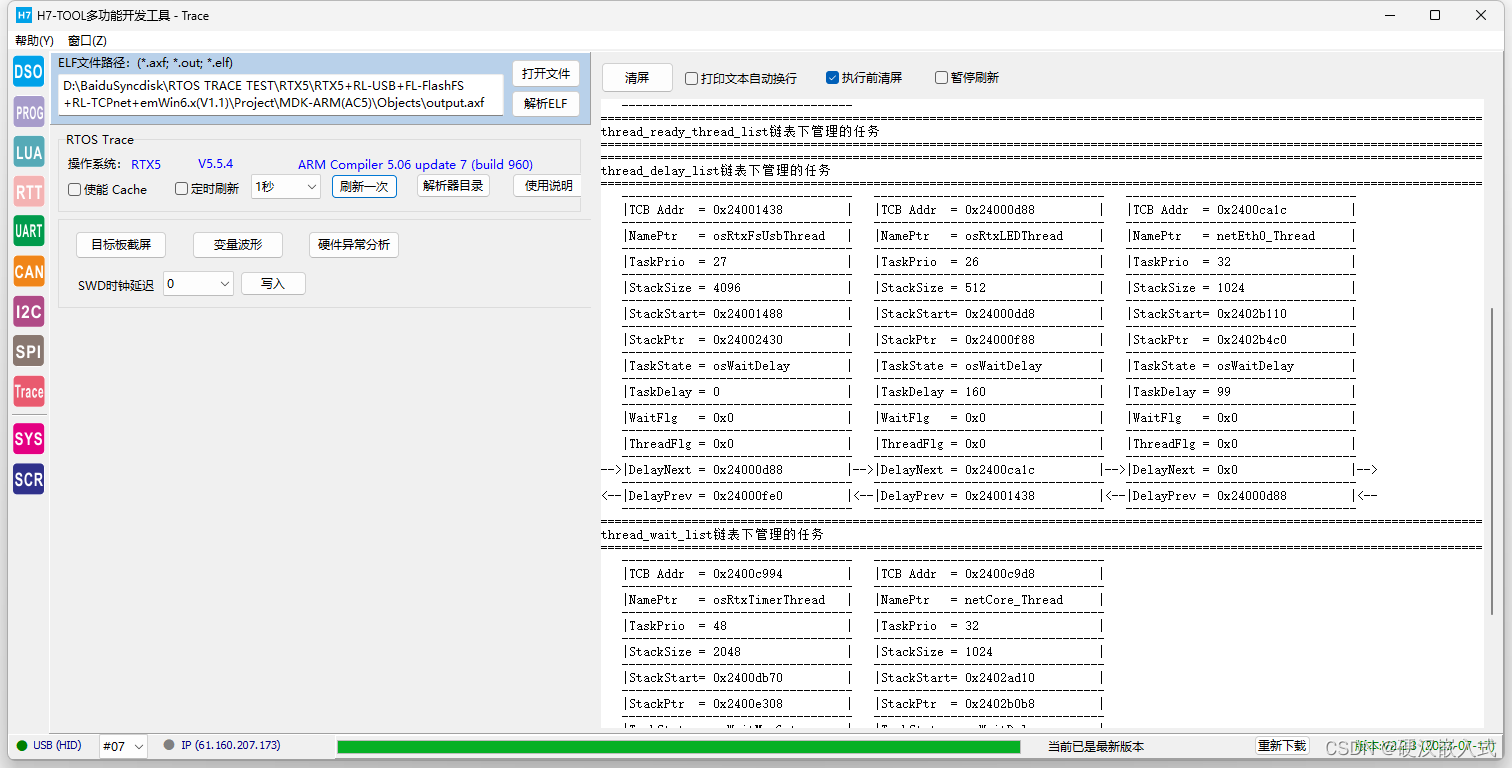
《安富莱嵌入式周报》第320期:键盘敲击声解码, 军工级boot设计,开源CNC运动控制器,C语言设计笔记,开源GPS车辆跟踪器,一键生成RTOS任务链表
周报汇总地址:嵌入式周报 - uCOS & uCGUI & emWin & embOS & TouchGFX & ThreadX - 硬汉嵌入式论坛 - Powered by Discuz! 视频版: https://www.bilibili.com/video/BV1Cr4y1d7Mp/ 《安富莱嵌入式周报》第320期:键盘敲击…...
DRF 缓存
应用环境 django4.2.3 ,python3.10 由于对于服务而言,有些数据查询起来比较费时,所以,对于有些数据,我们需要将其缓存。 最近做了一个服务,用的时 DRF 的架构,刚好涉及缓存,特此记…...

Collada .dae文件格式简明教程【3D】
当你从互联网下载 3D 模型时,可能会在格式列表中看到 .dae 格式。 它是什么? 推荐:用 NSDT编辑器 快速搭建可编程3D场景。 1、Collada DAE概述 COLLADA是COLLAborative Design Activity(中文:协作设计活动)…...

在K8s上处理nginx
基本说明 创建一个名为ssl的TLS类型的Secret对象,用于存储证书和密钥信息。 kubectl create secret tls ssl --certserver.crt --keyserver.key配置Nginx的events块,设置worker连接数为1024。 events {worker_connections 1024; }配置Nginx的http块&a…...
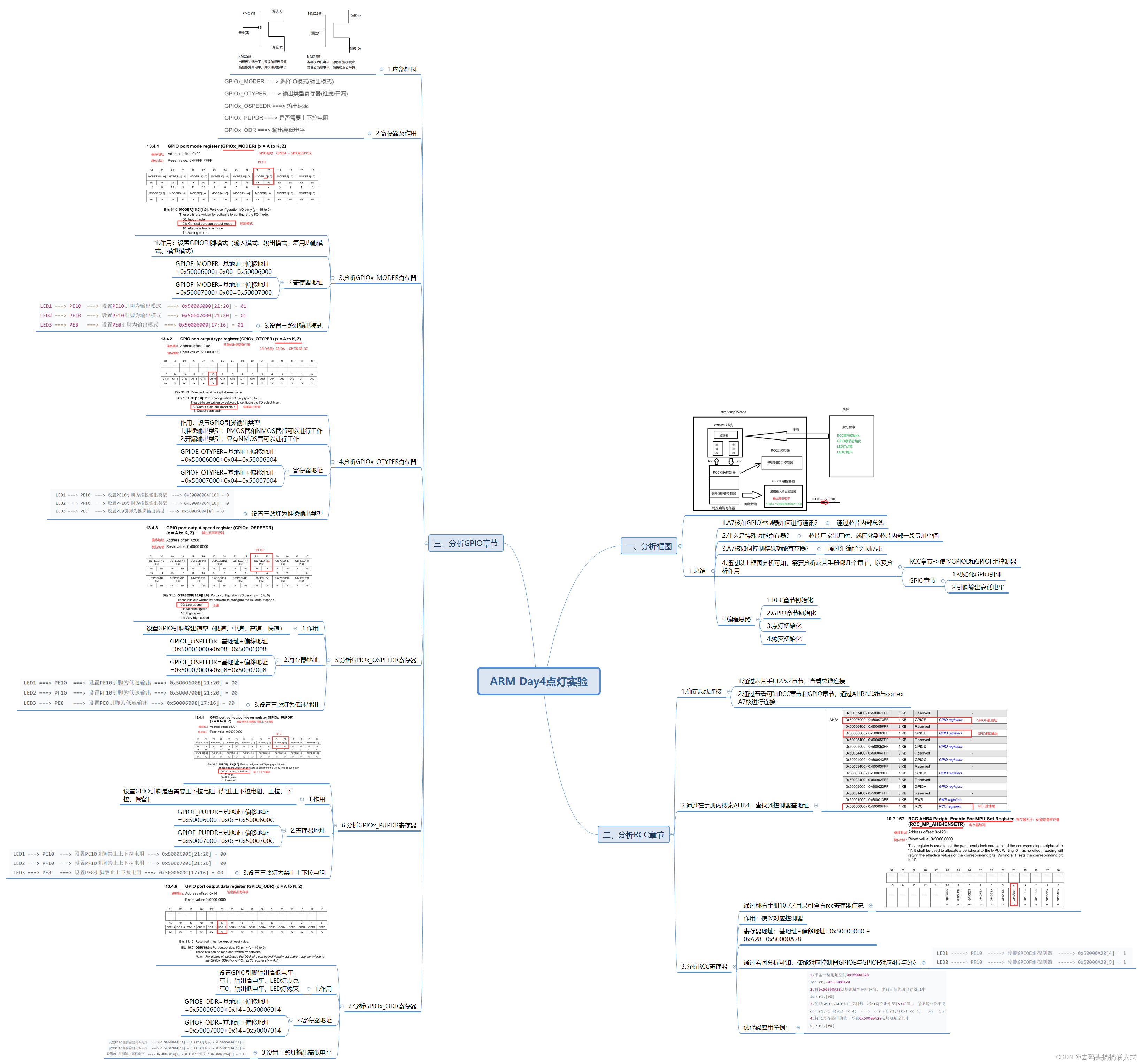
嵌入式:ARM Day4
一、自己编写代码实现三盏灯点亮 源码: .text .global _start _start: 进行一次初始化bl RCC_INITbl LED1_INITbl LED2_INITbl LED3_INITb looploop: 循环开关灯bl LED1_ONbl delay_1sbl LED1_OFFbl delay_1sbl LED2_ONbl delay_1sbl LED2_OFFbl delay_1sbl…...

SpringBoot案例-员工管理-分页条件查询
根据页面原型,明确需求 页面原型 需求 查看接口文档 接口文档的链接如下: 【腾讯文档】SpringBoot案例所需文档 https://docs.qq.com/doc/DUkRiTWVaUmFVck9N 思路分析 分页条件查询就时将条件查询的结果进行分页展示,由于有的条件可能设…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

门静脉高压——表现
一、门静脉高压表现 00:01 1. 门静脉构成 00:13 组成结构:由肠系膜上静脉和脾静脉汇合构成,是肝脏血液供应的主要来源。淤血后果:门静脉淤血会同时导致脾静脉和肠系膜上静脉淤血,引发后续系列症状。 2. 脾大和脾功能亢进 00:46 …...
