2023年美赛C题Wordle预测问题一建模及Python代码详细讲解

相关链接
(1)2023年美赛C题Wordle预测问题一建模及Python代码详细讲解
(2)2023年美赛C题Wordle预测问题二建模及Python代码详细讲解
(3)2023年美赛C题Wordle预测问题三、四建模及Python代码详细讲解
(4)2023年美赛C题Wordle预测问题25页论文
C题:Wordle预测
代码运行环境
编译器:vsCode
编程语言:Python
如果要运行代码,出现错误了,不要着急,百度一下错误,一般都是哪个包没有安装,用conda命令或者pip命令都能安装上。
1、问题一
1.1 第一小问
第一小问,建立一个时间序列预测模型,首先对数据按先后顺序排序,查看数据分布
import pandas as pd
import datetime as dt
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import skew,kurtosispd.options.display.notebook_repr_html=False # 表格显示
plt.rcParams['figure.dpi'] = 75 # 图形分辨率
sns.set_theme(style='darkgrid') # 图形主题df = pd.read_excel('data/Problem_C_Data_Wordle.xlsx',header=1)
data = df.drop(columns='Unnamed: 0')
data['Date'] = pd.to_datetime(data['Date'])
data.set_index("Date", inplace=True)
data.sort_index(ascending=True,inplace=True)
data

(1)查看数据分布
sns.lineplot(x="Date", y="Number of reported results",data=data)
plt.savefig('img/1.png',dpi=300)
plt.show()

(2)使用箱线图进行查看异常值,300000以上是异常值,黑色的,需要进行处理,本代码中采用的向前填充法,就是用异常值前一天的数据来填充。
sns.boxplot(data['Number of reported results'],color='red')
plt.savefig('img/2.png',dpi=300)

(3)因为Number of reported results是数值特征,在线性回归模型中,为了取得更好的建模效果,在建立回归评估模型之前,应该检查确认样本的分布,如果符合正态分布,则这种训练集是及其理想的,否则应该补充完善训练集或者通过技术手段对训练集进行优化。由KDE图和Q-Q图可知,价格属性呈右偏分布且不服从正态部分,在回归之前需要对数据进一步数据转换。
import scipy.stats as st
plt.figure(figsize=(20, 6))
y = data.Numbers
plt.subplot(121)
plt.title('johnsonsu Distribution fitting',fontsize=20)
sns.distplot(y, kde=False, fit=st.johnsonsu, color='Red')y2 = data.Numbers
plt.subplot(122)
st.probplot(y2, dist="norm", plot=plt)
plt.title('Q-Q Figure',fontsize=20)
plt.xlabel('X quantile',fontsize=15)
plt.ylabel('Y quantile',fontsize=15)
plt.savefig('img/5.png',dpi=300)
plt.show()
转换前

转换后,注意,预测得到的结果,还要转换回来,采用指数转换。公式是log(x) =y,x=e^y。
import scipy.stats as st
plt.figure(figsize=(20, 6))
y = np.log(data.Numbers)
plt.subplot(121)
plt.title('johnsonsu Distribution fitting',fontsize=20)
sns.distplot(y, kde=False, fit=st.johnsonsu, color='Red')y2 = np.log(data.Numbers)
plt.subplot(122)
st.probplot(y2, dist="norm", plot=plt)
plt.title('Q-Q Figure',fontsize=20)
plt.xlabel('X quantile',fontsize=15)
plt.ylabel('Y quantile',fontsize=15)
plt.savefig('img/6.png',dpi=300)
plt.show()

(4)可视化所有特征与label的相关性,采用皮尔逊相关性方法,筛选相关性较高作为数据集的特征。得到41个特征。
# 可视化Top20相关性最高的特征
df =data.copy()
corr = df[["target_t1"]+features].corr().abs()
k = 15
col = corr.nlargest(k,'target_t1')['target_t1'].index
plt.subplots(figsize = (10,10))
plt.title("Pearson correlation with label")
sns.heatmap(df[col].corr(),annot=True,square=True,annot_kws={"size":14},cmap="YlGnBu")
plt.savefig('img/10.png',dpi=300)
plt.show()

(5)划分数据集前,需要标准化特征数据,标准化后,将1-11月的数据作为训练集,12月的数据作为测试集。可以看到用简单线性回归可以拟合曲线。
data_feateng = df[features + targets].dropna()
nobs= len(data_feateng)
print("样本数量: ", nobs)
X_train = data_feateng.loc["2022-1":"2022-11"][features]
y_train = data_feateng.loc["2022-1":"2022-11"][targets]X_test = data_feateng.loc["2022-12"][features]
y_test = data_feateng.loc["2022-12"][targets]n, k = X_train.shape
print("Train: {}{}, \nTest: {}{}".format(X_train.shape, y_train.shape,X_test.shape, y_test.shape))plt.plot(y_train.index, y_train.target_t1.values, label="train")
plt.plot(y_test.index, y_test.target_t1.values, label="test")
plt.title("Train/Test split")
plt.legend()
plt.xticks(rotation=45)
plt.savefig('img/11.png',dpi=300)
plt.show()

(5)采用线性回归
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_errorX_train = data_feateng.loc["2022-1":"2022-11"][features]
y_train = data_feateng.loc["2022-1":"2022-11"][targets]X_test = data_feateng.loc["2022-12"][features]
y_test = data_feateng.loc["2022-12"][targets]
reg = LinearRegression().fit(X_train, y_train["target_t1"])
p_train = reg.predict(X_train)
p_test = reg.predict(X_test)y_pred = np.exp(p_test*std+mean)
y_true = np.exp(y_test["target_t1"]*std+mean)RMSE_test = np.sqrt(mean_squared_error(y_true,y_pred))
print("Test RMSE: {}".format(RMSE_test))
模型误差是RMSE: 1992.293296317915
模型训练和预测
from sklearn.linear_model import LinearRegression
reg = LinearRegression().fit(X_train, y_train["target_t1"])
p_train = reg.predict(X_train)
arr = np.array(X_test).reshape((1,-1))
p_test = reg.predict(arr)y_pred = np.exp(p_test*std+mean)
print(f"预测区间是[{int(y_pred-RMSE_test)}至{int(y_pred+int(RMSE_test))}]")
预测得到的结果减去误差,得到预测区间的左边界,加上误差,得到预测区间的右边界。最后得出的预测区间是【18578-22562】
1.2 第二小问
我提取了每个单词中每个字母位置的特征(如a编码为1,b编码为2,c编码为3依次类推,z编码为26,那5个单词的位置就填入相应的数值,类似于ont-hot编码)、元音的字母的频率(五个单词中元音字母出现了几次),辅音字母的频率(5个单词中辅音字母出现了几次),还有一个是单词的词性(形容词,副词,名词等等,这部分没有做)
特征在代码中未这几个:‘w1’,‘w2’,‘w3’,‘w4’,‘w5’,‘Vowel_fre’,‘Consonant_fre’
然后分别计算1-7次尝试百分比与这几个特征的相关性,采用皮尔逊相关性方法。同学们,继续对图片中的数值进行解读,应用到论文中,可以用表格阐述。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as snsdf = pd.read_excel('data/Problem_C_Data_Wordle.xlsx',header=1)
data = df.drop(columns='Unnamed: 0')
data['Date'] = pd.to_datetime(data['Date'])
df.set_index('Date',inplace=True)
df.sort_index(ascending=True,inplace=True)
df =data.copy()
df['Words'] = df['Word'].apply(lambda x:str(list(x))[1:-1].replace("'","").replace(" ",""))
df['w1'], df['w2'],df['w3'], df['w4'],df['w5'] = df['Words'].str.split(',',n=4).str
df

small = [str(chr(i)) for i in range(ord('a'),ord('z')+1)]
letter_map = dict(zip(small,range(1,27)))
letter_map
{‘a’: 1, ‘b’: 2, ‘c’: 3, ‘d’: 4, ‘e’: 5, ‘f’: 6, ‘g’: 7, ‘h’: 8, ‘i’: 9, ‘j’: 10, ‘k’: 11, ‘l’: 12, ‘m’: 13, ‘n’: 14, ‘o’: 15, ‘p’: 16, ‘q’: 17, ‘r’: 18, ‘s’: 19, ‘t’: 20, ‘u’: 21, ‘v’: 22, ‘w’: 23, ‘x’: 24, ‘y’: 25, ‘z’: 26}
df['w1'] = df['w1'].map(letter_map)
df['w2'] = df['w2'].map(letter_map)
df['w3'] = df['w3'].map(letter_map)
df['w4'] = df['w4'].map(letter_map)
df['w5'] = df['w5'].map(letter_map)
df

(1)统计元音辅音频率
Vowel = ['a','e','i','o','u']
Consonant = list(set(small).difference(set(Vowel)))
def count_Vowel(s):c = 0for i in range(len(s)):if s[i] in Vowel:c+=1return c
def count_Consonant(s):c = 0for i in range(len(s)):if s[i] in Consonant:c+=1return cdf['Vowel_fre'] = df['Word'].apply(lambda x:count_Vowel(x))
df['Consonant_fre'] = df['Word'].apply(lambda x:count_Consonant(x))
df
(2)分析相关性
# 可视化Top20相关性最高的特征
features = ['w1','w2','w3','w4','w5','Vowel_fre','Consonant_fre']
label = ['1 try','6 tries','6 tries','6 tries','6 tries','6 tries','7 or more tries (X)']
n = 11
for i in label:corr = df[[i]+features].corr().abs()k = len(features)col = corr.nlargest(k,i)[i].indexplt.subplots(figsize = (10,10))plt.title(f"Pearson correlation with {i}")sns.heatmap(df[col].corr(),annot=True,square=True,annot_kws={"size":14},cmap="YlGnBu")plt.savefig(f'img/1/{n}.png',dpi=300)n+=1plt.show()







3 Code
Code获取,在浏览器中输入:betterbench.top/#/40/detail,或者Si我
剩下的问题二、三、四代码实现,在我主页查看,陆续发布出来。
相关文章:

2023年美赛C题Wordle预测问题一建模及Python代码详细讲解
相关链接 (1)2023年美赛C题Wordle预测问题一建模及Python代码详细讲解 (2)2023年美赛C题Wordle预测问题二建模及Python代码详细讲解 (3)2023年美赛C题Wordle预测问题三、四建模及Python代码详细讲解 &…...
小米12s ultra,索尼xperia1 iv,数码相机 拍照对比
首先说明所有的测试结果和拍摄数据我放到百度网盘了(地址在结尾) 为什么做这个测试 我一直想知道现在的手机和相机差距有多大,到底差在哪儿? 先说结论: 1.1英寸的手机cmos(2022年) 6年前(2016)的入门款相机(m43画幅) 2.手机 不能换镜头,只能在特定的拍摄距离才能发挥出全…...
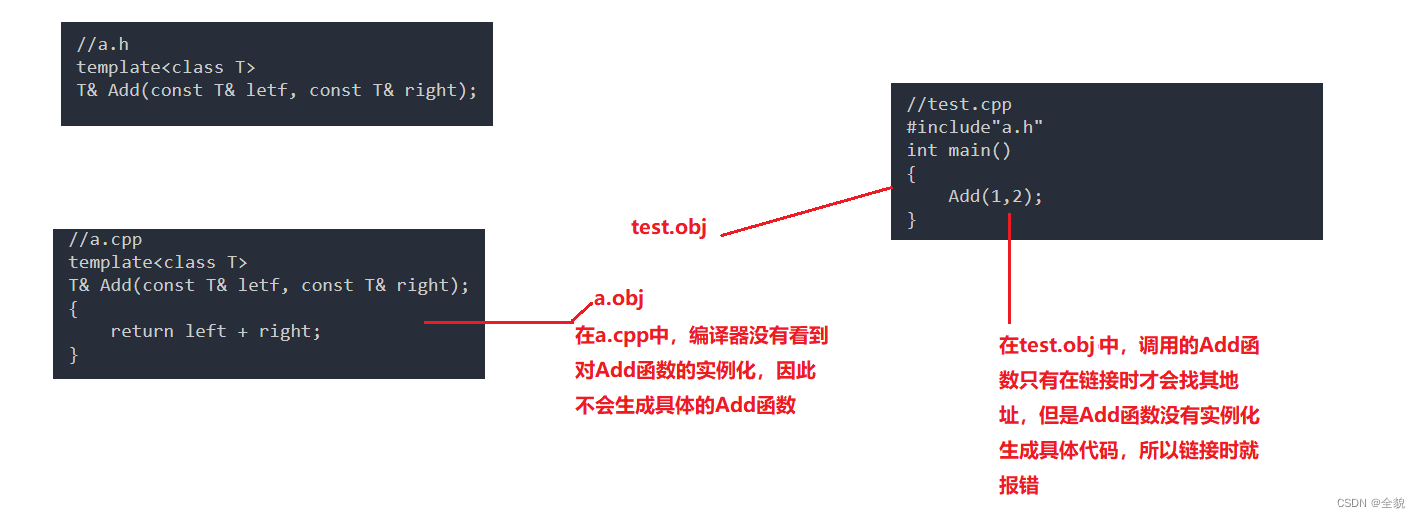
C++笔记 模板的进阶知识
目录 1. 非类型模板参数 2.模板的特化 2.1 函数模板的特化 2.2 类模板的特化 2.2.1 全特化 2.2.2 偏特化 3.模板的分离编译 3.1 什么是分离编译? 3.2 模板的分离编译 4.模板的总结 模板的初阶内容:(594条消息) C模板的原理和使用_全貌的博客-CSD…...
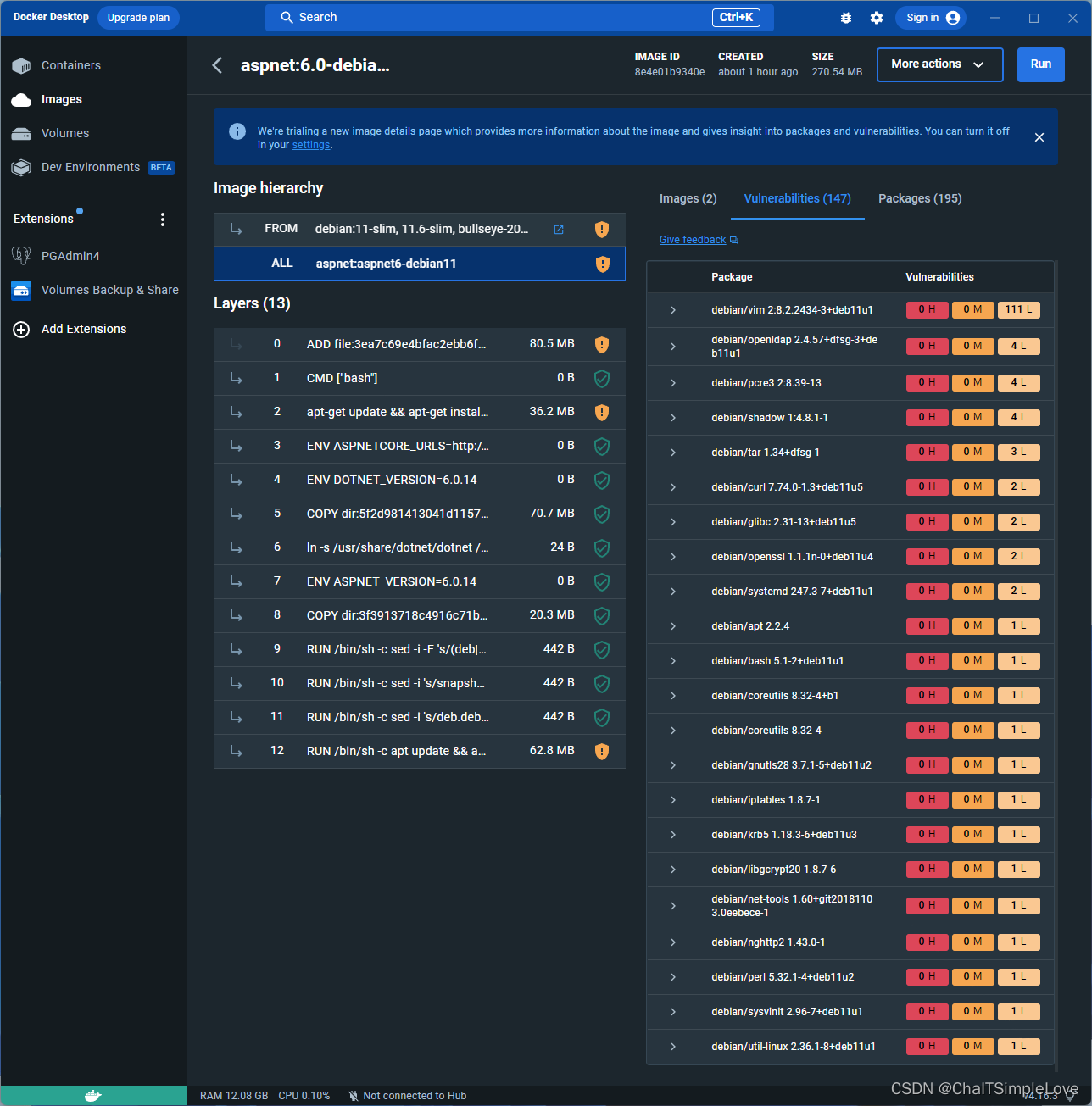
基于 Debain11 构建 asp.net core 6.x 的基础运行时镜像
基于 Debain11 构建 asp.net core 6.x 的基础运行时镜像Linux 环境说明Debian 简介Debian 发行版本关于 Debian 11Linux 常用基础工具Dockerfile 中 RUN 指令RUN 语法格式RUN 语义说明编写 Dockerfile 构建 Runtime 基础镜像ASP.NET Core Runtime 基础镜像Dockerfile 编写Windo…...
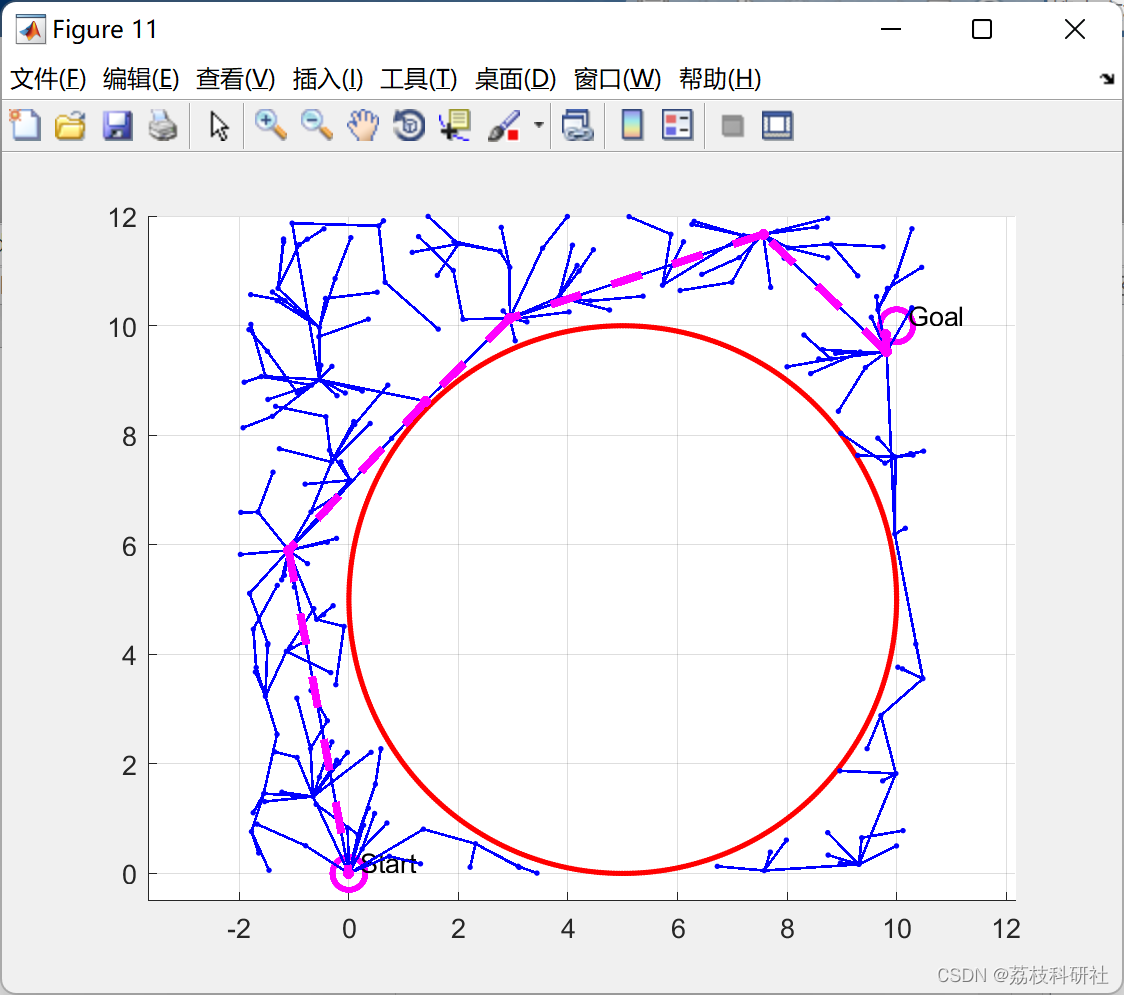
【无人机路径规划】基于IRM和RRTstar进行无人机路径规划(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
Spring Boot中使用@Autowire装配接口是怎么回事?
在学习使用Spring Boot框架时候,发现了一个特别的现象UserMapper是一个接口,在另一个类中好像直接使用Autowired装配了一个UserMapper对象???我纳闷了一会儿,接口居然可以直接实例对象吗?根据我…...
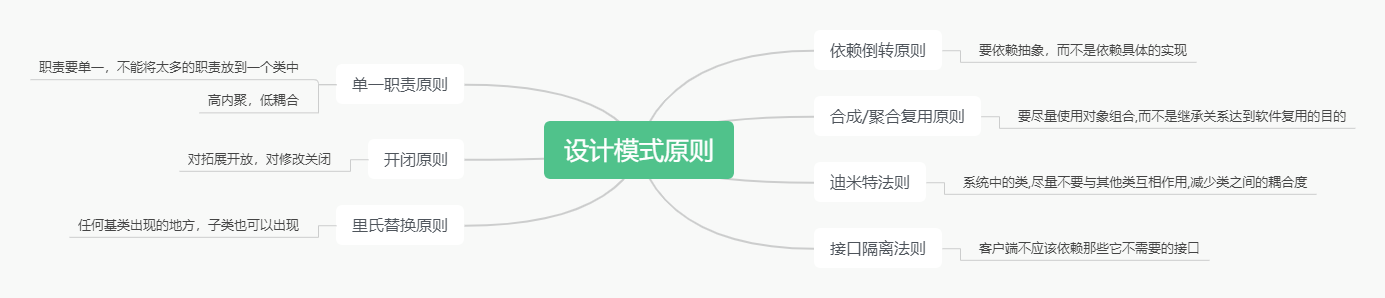
23种设计模式介绍(Python示例讲解)
文章目录一、概述二、设计模式七种原则三、设计模式示例讲解1)创建型模式1、工厂模式(Factory Method)【1】简单工厂模式(不属于GOF设计模式之一)【2】工厂方法模式2、抽象工厂模式(AbstractFactory&#x…...

初识Hadoop,走进大数据世界
文章目录数据!数据!遇到的问题Hadoop的出现相较于其他系统的优势关系型数据库网格计算本文章属于Hadoop系列文章,分享Hadoop相关知识。后续文章中会继续分享Hadoop的组件、MapReduce、HDFS、Hbase、Flume、Pig、Spark、Hadoop集群管理系统以及…...
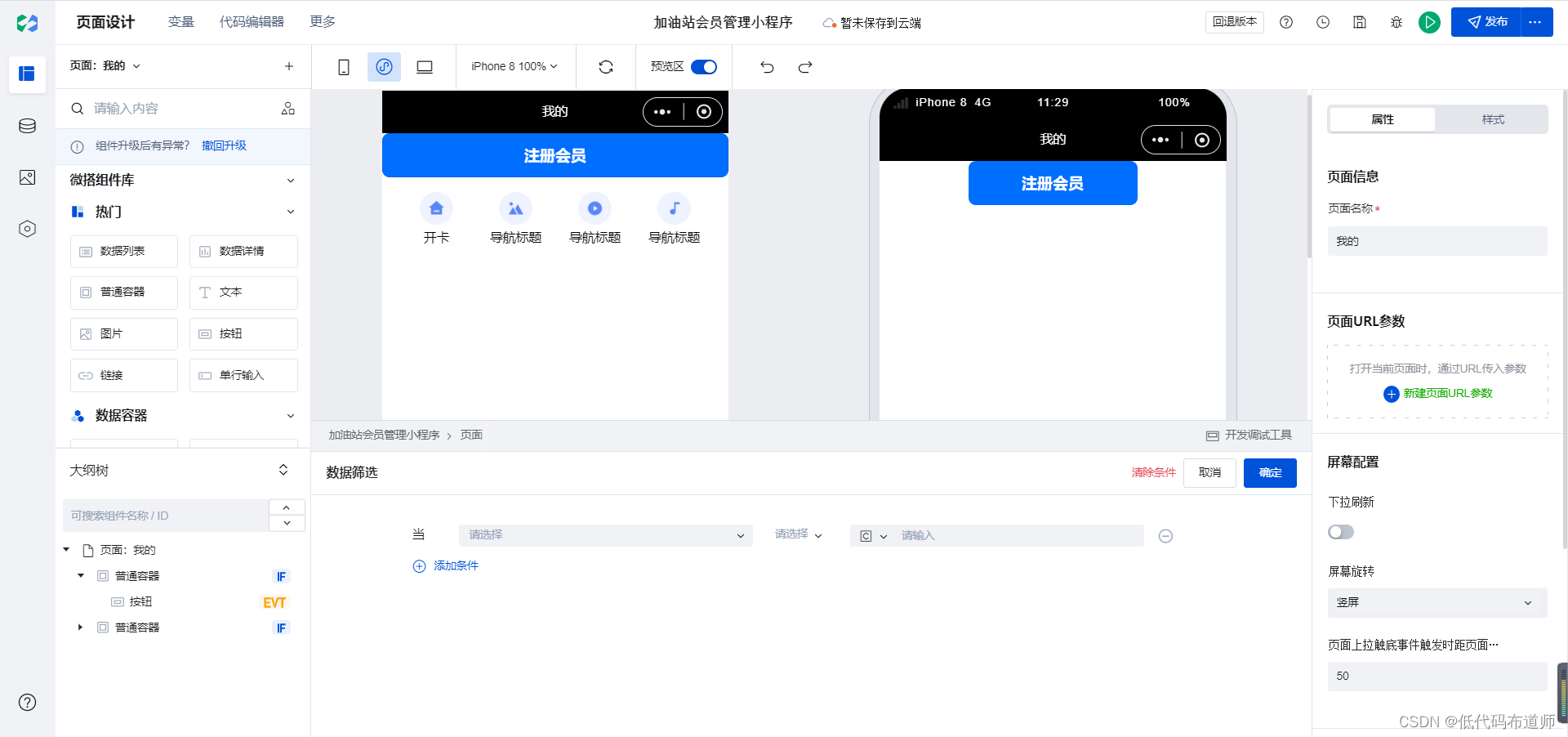
加油站会员管理小程序实战开发教程14 会员充值
我们上篇介绍了会员开卡的业务,开卡是为了创建会员卡的信息。有了会员卡信息后我们就可以给会员进行充值。当然了充值这个业务是由会员自主发起的。 按照我们的产品原型,我们在我的页面以轮播图的形式循环展示当前会员的所有卡信息。这个会员卡信息需要先用变量从数据源读取…...

leetcode 1792. 最大平均通过率
一所学校里有一些班级,每个班级里有一些学生,现在每个班都会进行一场期末考试。给你一个二维数组 classes ,其中 classes[i] [passi, totali] ,表示你提前知道了第 i 个班级总共有 totali 个学生,其中只有 passi 个学…...

15-基础加强-2-xml(约束)枚举注解
文章目录1.xml1.1概述【理解】(不用看)1.2标签的规则【应用】1.3语法规则【应用】1.4xml解析【应用】1.5DTD约束【理解】1.5.1 引入DTD约束的三种方法1.5.2 DTD语法(会阅读,然后根据约束来写)1.6 schema约束【理解】1.6.1 编写schema约束1.6.…...
)
13:高级篇 - CTK 事件管理机制(signal/slot)
作者: 一去、二三里 个人微信号: iwaleon 微信公众号: 高效程序员 在《12:高级篇 - CTK 事件管理机制(sendEvent/postEvent)》一文中,我们介绍了如何进行插件间通信 - sendEvent()/postEvent() + ctkEventHandler。然而,除了这种方式之外,EventAdmin 还提供了另一种方…...
群晖-第1章-IPV6的DDNS
群晖-第1章-IPV6的DDNS 方案:腾讯云群晖DS920 本文参考群晖ipv6 DDNS-go教程-牧野狂歌,感谢原作者的分享。 这篇文章只记录了我需要的部分,其他的可以查看原文,原文还记录了更多的内容,可能帮到你。 一、购买域名 …...
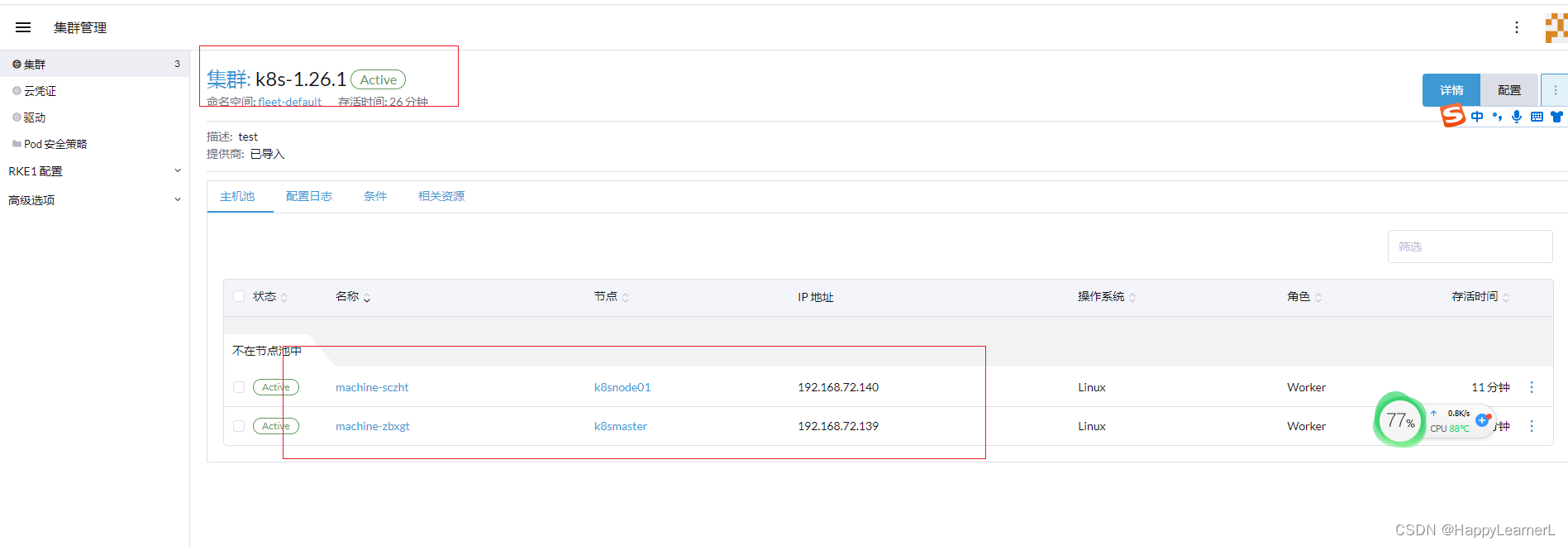
centos7系统-kubeadm安装k8s集群(v1.26版本)亲测有效,解决各种坑可供参考
文章目录硬件要求可省略的步骤配置虚拟机ip设置阿里镜像源各服务器初始化配置配置主节点的主机名称配置从节点的主机名称配置各节点的Host文件关闭各节点的防火墙关闭selinux永久禁用各节点的交换分区同步各节点的时间将桥接的IPv4流量传递到iptables的链(三台都执行…...
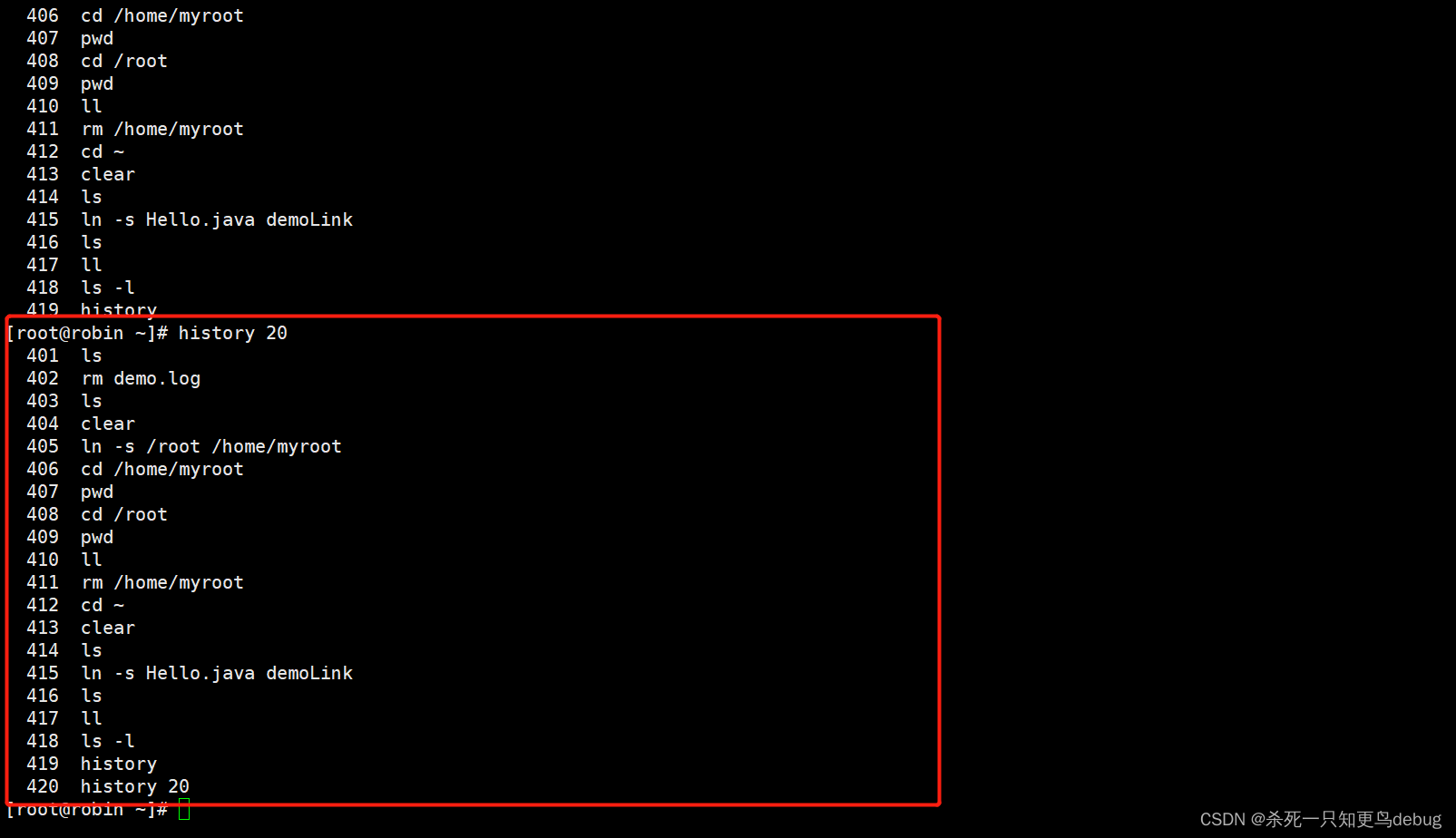
帮助指令 man ,help及文档常用管理指令
帮助指令 man,help 1. man 当我们想要了解某个命令如何使用,及选项的含义是什么以及配置文件的帮助信息时,可以使用 man [命令或配置文件],这样便可以获得到帮助提示信息了。 语法格式:man [命令或者配置文件] 比如…...
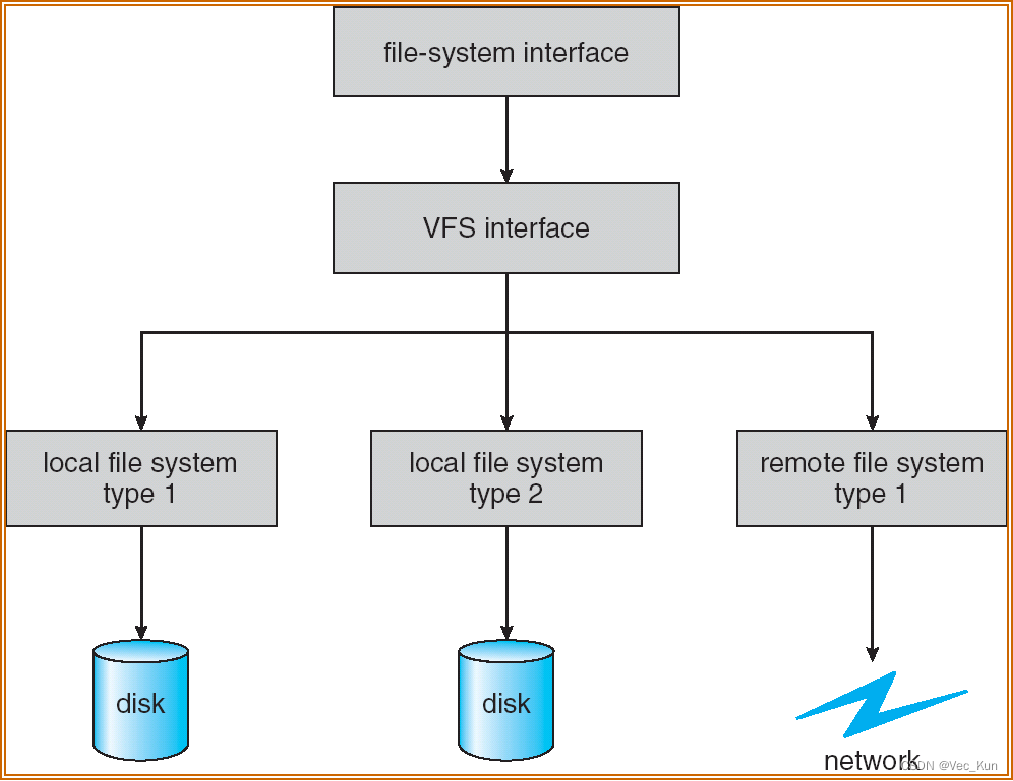
电子科技大学操作系统期末复习笔记(五):文件管理
目录 前言 文件管理:基础 基本概念 文件 文件系统 文件系统的实现模型 文件的组成 文件名 文件分类 文件结构 逻辑结构 物理结构 练习题 文件管理:目录 文件控制块FCB FCB:File Control Block FCB信息 目录 基本概念 目…...
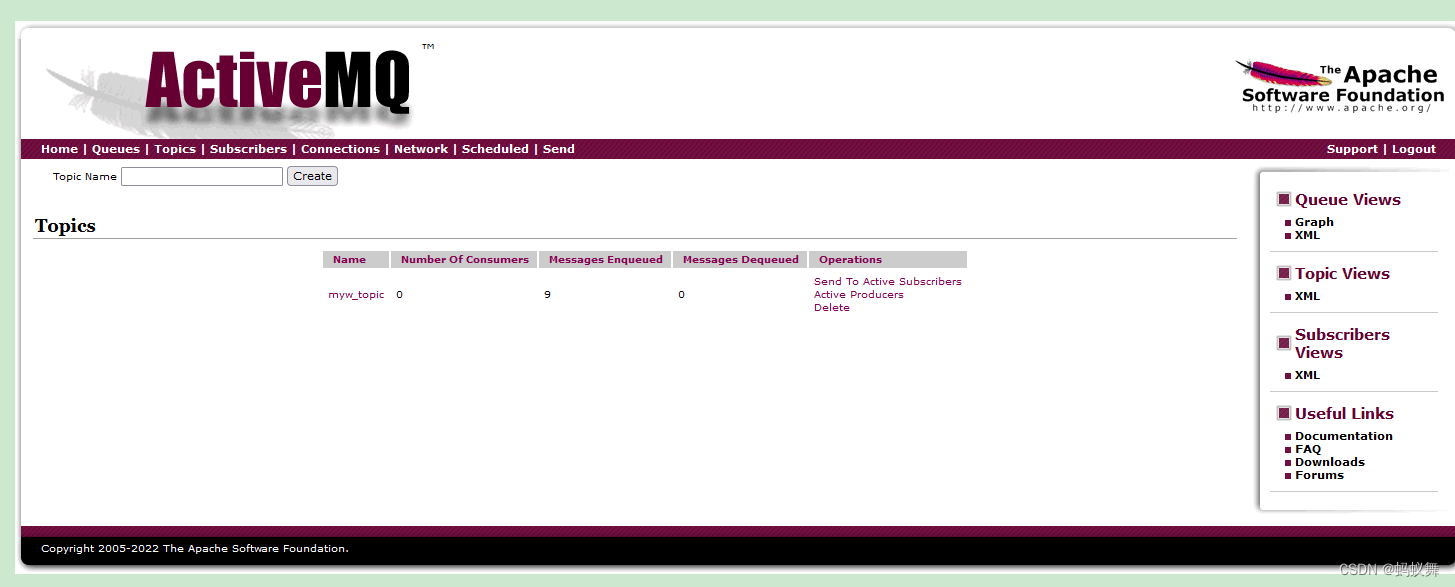
SpringBoot+ActiveMQ-发布订阅模式(生产端)
SpringBootActiveMQ-发布订阅模式(生产端)Topic 主题* 消息消费者(订阅方式)消费该消息* 消费生产者将发布到topic中,同时有多个消息消费者(订阅)消费该消息* 这种方式和点对点方式不同…...
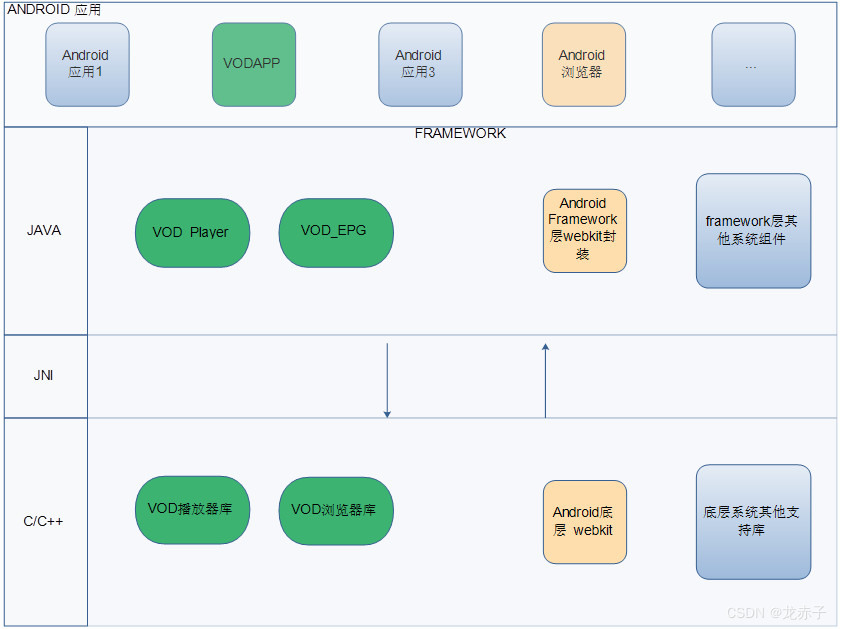
Android实例仿真之三
目录 四 Android架构探究 五 大骨架仿真 六 Android实例分析思路拓展 四 Android架构探究 首先,Android系统所带来的好处,就在于它本身代码的开放性,这提供了一个学习、借鉴的平台。这对分析仿真而言,本身就是一大利好…...
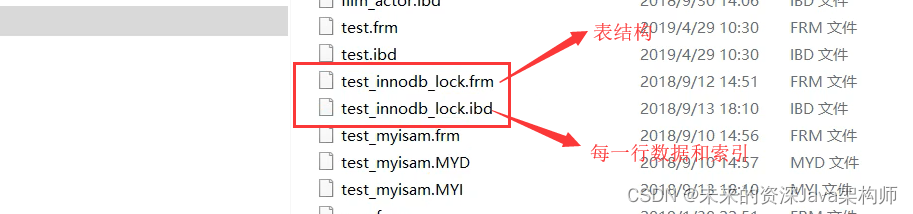
关于MySQL的limit优化
1、前提 提示:只适用于InnoDB引擎 2、InnoDB存储特点 它把索引和数据放在了一个文件中,就是聚集索引。这与MyISAM引擎是不一样的。 3、SQL示例 -- 给cve字段建立索引 select * from cnnvd where cveCVE-2022-24808 limit 300000,10;由于M…...

Java-Stream流基本使用
collection.stream将会破坏原有的数据结构,可以通过collect方法收集,可以用Collectors提供的构造器,add等方法构造形成新的数据结构。 HashSet<List<Integer>> rs new HashSet<>(); rs.stream().toList();Collection集合转…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...
