势函数和鞅的停时定理
前置芝士
鞅:
鞅是一类特殊的随机过程,假设我们从一开始就在观察一场赌博游戏,现在已经得到了前t秒的观测值,那么当第t+1 秒观测值的期望等于第t秒的观测值时,我们称这是一个公平赌博游戏。
具体来说,对于一个随机过程 A 1 , A 2 , . . . {A_1,A_2,...} A1,A2,...,如果 E ( A n + 1 ∣ A 0 , A 2 , . . A n ) = A n E(A_{n+1}|A_0,A_2,..A_n)=A_n E(An+1∣A0,A2,..An)=An,我们称该随机过程为鞅。
鞅的停时定理:
设时停时间(在不知道随机过程的中间状态下停止的时刻)为t,则 E ( t ) = E ( 0 ) E(t)=E(0) E(t)=E(0)
这个E到底是什么,由具体的情境而定,但是只要一个随机过程是一个鞅,它就有该结论
势函数
接下来我们考虑一个很常见的问题:
对于一个随机过程 A 1 , A 2 , . . . {A_1,A_2,...} A1,A2,...,如果其终止状态 A t A_t At是确定的,求 E [ t ] E[t] E[t],即时停时刻的期望(注意这里我们不要求该随机过程是一个鞅)
为此,我们引入一个势函数 ϕ ( X ) \phi(X) ϕ(X)
并且 ϕ ( x ) \phi(x) ϕ(x)满足如下性质:
- ∀ n < t , E ( ϕ ( A n + 1 ) − ϕ ( A n ) ∣ A 0 , A 1 , . . . A n ) = − 1 \forall n<t, E(\phi(A_{n+1})-\phi(A_n)|A_0,A_1,...A_n)=-1 ∀n<t,E(ϕ(An+1)−ϕ(An)∣A0,A1,...An)=−1,即势能不断降低
- E ( ϕ ( A t ) ) = C E(\phi(A_t))=C E(ϕ(At))=C,是一个常值
那么如果我们令 X t = ϕ ( A t ) + t X_t=\phi(A_t)+t Xt=ϕ(At)+t,则 E ( X n + 1 − X n ∣ x 0 , x 1 . . . x n ) = E ( ϕ ( A n + 1 ) − ϕ ( A n ) + 1 ∣ x 0 , x 1 . . . x n ) = E ( ϕ ( A n + 1 ) − ϕ ( A n ) ∣ x 0 , x 1 . . . x n ) + 1 = 0 E(X_{n+1}-X_n|x_0,x_1...x_n)=E(\phi(A_{n+1})-\phi(A_n)+1|x_0,x_1...x_n)=E(\phi(A_{n+1})-\phi(A_n)|x_0,x_1...x_n)+1=0 E(Xn+1−Xn∣x0,x1...xn)=E(ϕ(An+1)−ϕ(An)+1∣x0,x1...xn)=E(ϕ(An+1)−ϕ(An)∣x0,x1...xn)+1=0
我们发现随机过程 X t X_t Xt就是一个鞅了
那么由鞅的停时原理, E ( X t ) = E ( X 0 ) E(X_t)=E(X_0) E(Xt)=E(X0),即 E ( ϕ ( A t ) + t ) = E ( ϕ ( A 0 ) + 0 ) E(\phi(A_t)+t)=E(\phi(A_0)+0) E(ϕ(At)+t)=E(ϕ(A0)+0),也即 E ( ϕ ( A t ) ) + E ( t ) = E ( ϕ ( A 0 ) ) E(\phi(A_t))+E(t)=E(\phi(A_0)) E(ϕ(At))+E(t)=E(ϕ(A0))
所以我们得到 E ( t ) = E ( ϕ ( A 0 ) ) − E ( ϕ ( A t ) ) E(t)=E(\phi(A_0))-E(\phi(A_t)) E(t)=E(ϕ(A0))−E(ϕ(At)),根据我们之前定义的性质, E ( ϕ ) A t E(\phi)A_t E(ϕ)At为一个常值,而 E ( ϕ ( A 0 ) ) E(\phi(A_0)) E(ϕ(A0))显然也是一个常值,所以只要能找到这个满足条件的势函数,就能很方便的求出 E ( t ) E(t) E(t)
这里我们只是在随机过程 X t X_t Xt中应用了停时定理,对原本的随机过程 A t A_t At并没有做什么限制
接下来结合具体的题目来讨论一下如何构造这样的一个势函数
CF1349D
大意:
有n个人在玩传球游戏,一开始第 i i i个人有 a i a_i ai个球。每一次传球,等概率随机选中一个球,设其当前拥有者为 i i i, i i i将这个球等概率随机传给另一个人 j ( j ≠ i ) j(j\neq i) j(j=i)。当某一个人拥有所有球时,停止游戏。问游戏停止时的期望传球次数。
记球的总数为m
不妨记状态 A t = ( a t , 1 , a t , 2 . . . a t , n ) A_t=(a_{t,1},a_{t,2}...a_{t,n}) At=(at,1,at,2...at,n),一个n维向量,分别表示 在时刻t,第i个人手中球的数量,显然它唯一地表示了某一个时刻的全局状态
也就是说,我们现在就把这个游戏过程抽象成了一个随机过程 A 0 , A 1 . . . . A_0,A_1.... A0,A1....,并且其停时为t。那么按照之前所说,我们需要去定义一个势函数 ϕ ( A t ) \phi(A_t) ϕ(At),为了计算方便,我们可以将 ϕ \phi ϕ具体到A的每一维向量,不妨记为 ϕ ( A t ) = ∑ i = 1 n f ( a t , i ) \phi(A_t)=\sum_{i=1}^{n}f(a_{t,i}) ϕ(At)=∑i=1nf(at,i),这里f是什么我们并不知道,但是如果我们知道了f,其实也就是相当于构造出了这个势能函数
这里再把我们定义的 ϕ \phi ϕ的性质再放一下
ϕ ( x ) \phi(x) ϕ(x)满足如下性质:
- ∀ n < t , E ( ϕ ( A n + 1 ) − ϕ ( A n ) ∣ A 0 , A 1 , . . . A n ) = − 1 \forall n<t, E(\phi(A_{n+1})-\phi(A_n)|A_0,A_1,...A_n)=-1 ∀n<t,E(ϕ(An+1)−ϕ(An)∣A0,A1,...An)=−1,即势能不断降低
- E ( ϕ ( A t ) ) = C E(\phi(A_t))=C E(ϕ(At))=C,是一个常值
那么我们首先来考虑第一个性质,为了方便,不妨先考虑 E ( ϕ ( A n + 1 ) ∣ A 0 , A 1 , . . . A n ) E(\phi(A_{n+1})|A_0,A_1,...A_n) E(ϕ(An+1)∣A0,A1,...An)
发现传球过程就是一个 M a r k o v Markov Markov过程,并且该时刻的状态只与上一个时刻的状态有关,所以 E ( ϕ ( A n + 1 ) ∣ A 0 , A 1 , . . . A n ) = E ( ϕ ( A n + 1 ) ∣ A n ) E(\phi(A_{n+1})|A_0,A_1,...A_n)=E(\phi(A_{n+1})|A_n) E(ϕ(An+1)∣A0,A1,...An)=E(ϕ(An+1)∣An)
考虑一次转移的所有可能
i传球给j的概率是 a t , i m 1 n − 1 \large \frac{a_{t,i}}{m}\frac{1}{n-1} mat,in−11
E ( ϕ ( A n + 1 ) ∣ A n ) = ∑ i = 1 n ∑ j ≠ i a t , i m 1 n − 1 [ f ( a t , i − 1 ) + f ( a t , j + 1 ) + ∑ k ∉ ( i , j ) f ( a t , k ) ] E(\phi(A_{n+1})|A_n)=\sum_{i=1}^{n}\sum_{j\neq i}\frac{a_{t,i}}{m}\frac{1}{n-1}[f(a_{t,i}-1)+f(a_{t,j}+1)+\sum_{k\notin(i,j)}f(a_{t,k})] E(ϕ(An+1)∣An)=∑i=1n∑j=imat,in−11[f(at,i−1)+f(at,j+1)+∑k∈/(i,j)f(at,k)]
= ∑ i = 1 n a t , i m f ( a t , i − 1 ) + m − a t , i m ( n − 1 ) f ( a t , i + 1 ) + ( m − a t , i ) ( n − 2 ) m ( n − 1 ) f ( a t , i ) =\sum_{i=1}^{n}\frac{a_{t,i}}{m}f(a_{t,i}-1)+\frac{m-a_{t,i}}{m(n-1)}f(a_{t,i}+1)+\frac{(m-a_{t,i})(n-2)}{m(n-1)}f(a_{t,i}) =∑i=1nmat,if(at,i−1)+m(n−1)m−at,if(at,i+1)+m(n−1)(m−at,i)(n−2)f(at,i)
根据我们定义的性质 E ( ϕ ( A n + 1 ) − ϕ ( A n ) ∣ A 0 , A 1 , . . . A n ) = − 1 E(\phi(A_{n+1})-\phi(A_n)|A_0,A_1,...A_n)=-1 E(ϕ(An+1)−ϕ(An)∣A0,A1,...An)=−1
E ( ϕ ( A n + 1 ) − ϕ ( A n ) ∣ A 0 , A 1 , . . . A n ) = E ( ϕ ( A n + 1 ) − ϕ ( A n ) ∣ A n ) E(\phi(A_{n+1})-\phi(A_n)|A_0,A_1,...A_n)=E(\phi(A_{n+1})-\phi(A_n)|A_n) E(ϕ(An+1)−ϕ(An)∣A0,A1,...An)=E(ϕ(An+1)−ϕ(An)∣An)
= ( ∑ i = 1 n a t , i m f ( a t , i − 1 ) + m − a t , i m ( n − 1 ) f ( a t , i + 1 ) + ( m − a t , i ) ( n − 2 ) m ( n − 1 ) f ( a t , i ) ) − ∑ f ( a t , i ) = − 1 =(\sum_{i=1}^{n}\frac{a_{t,i}}{m}f(a_{t,i}-1)+\frac{m-a_{t,i}}{m(n-1)}f(a_{t,i}+1)+\frac{(m-a_{t,i})(n-2)}{m(n-1)}f(a_{t,i}))-\sum f(a_{t,i})=-1 =(∑i=1nmat,if(at,i−1)+m(n−1)m−at,if(at,i+1)+m(n−1)(m−at,i)(n−2)f(at,i))−∑f(at,i)=−1
所以 ∑ f ( a t , i ) = ( ∑ i = 1 n a t , i m f ( a t , i − 1 ) + m − a t , i m ( n − 1 ) f ( a t , i + 1 ) + ( m − a t , i ) ( n − 2 ) m ( n − 1 ) f ( a t , i ) ) + 1 \sum f(a_{t,i})=(\sum_{i=1}^{n}\frac{a_{t,i}}{m}f(a_{t,i}-1)+\frac{m-a_{t,i}}{m(n-1)}f(a_{t,i}+1)+\frac{(m-a_{t,i})(n-2)}{m(n-1)}f(a_{t,i}))+1 ∑f(at,i)=(∑i=1nmat,if(at,i−1)+m(n−1)m−at,if(at,i+1)+m(n−1)(m−at,i)(n−2)f(at,i))+1
那么我们可以把末尾的1分配到每一个和式里面去,这样左右的形式就统一了
所以 ∑ f ( a t , i ) = ∑ i = 1 n [ a t , i m f ( a t , i − 1 ) + m − a t , i m ( n − 1 ) f ( a t , i + 1 ) + ( m − a t , i ) ( n − 2 ) m ( n − 1 ) f ( a t , i ) + a t , i n ] \sum f(a_{t,i})=\sum_{i=1}^{n}[\frac{a_{t,i}}{m}f(a_{t,i}-1)+\frac{m-a_{t,i}}{m(n-1)}f(a_{t,i}+1)+\frac{(m-a_{t,i})(n-2)}{m(n-1)}f(a_{t,i})+\frac{a_{t,i}}{n}] ∑f(at,i)=∑i=1n[mat,if(at,i−1)+m(n−1)m−at,if(at,i+1)+m(n−1)(m−at,i)(n−2)f(at,i)+nat,i]
那么不妨记 f ( a ) = a m f ( a − 1 ) + m − a m ( n − 1 ) f ( a + 1 ) + ( m − a ) ( n − 2 ) m ( n − 1 ) f ( a ) + a n f(a)=\frac{a}{m}f(a-1)+\frac{m-a}{m(n-1)}f(a+1)+\frac{(m-a)(n-2)}{m(n-1)}f(a)+\frac{a}{n} f(a)=maf(a−1)+m(n−1)m−af(a+1)+m(n−1)(m−a)(n−2)f(a)+na
这样和式还是成立的,我们也成功抽象出了f函数
再转化一下, f ( a + 1 ) = m + a n − 2 a m − a f ( a ) − a ( n − 1 ) m − a ( f ( a − 1 ) + 1 ) f(a+1)=\frac{m+an-2a}{m-a}f(a)-\frac{a(n-1)}{m-a}(f(a-1)+1) f(a+1)=m−am+an−2af(a)−m−aa(n−1)(f(a−1)+1)
代入边界条件 a = 0 a=0 a=0时,有 f ( 1 ) = f ( 0 ) f(1)=f(0) f(1)=f(0),所以我们可以设 f ( 1 ) = f ( 0 ) = 0 f(1)=f(0)=0 f(1)=f(0)=0,毕竟势函数的初值并不重要
这样就得到了f,也就是相当于得到了势函数 ϕ ( x t ) = ∑ i f ( x t , i ) \phi(x_t)=\sum_{i}f(x_{t,i}) ϕ(xt)=∑if(xt,i)
然后考虑势函数的第二个性质: E ( ϕ ( A t ) ) = C E(\phi(A_t))=C E(ϕ(At))=C是一个常值
显然 E ( ϕ ( A t ) ) = ∑ i f ( a t , i ) = f ( m ) + ( n − 1 ) f ( 0 ) E(\phi(A_t))=\sum_{i}f(a_{t,i})=f(m)+(n-1)f(0) E(ϕ(At))=∑if(at,i)=f(m)+(n−1)f(0)是一个常值
所以根据我们的结论, E ( t ) = E ( ϕ ( A 0 ) ) − E ( ϕ ( A t ) ) = ∑ i f ( a 0 , i ) − f ( m ) − ( n − 1 ) f ( 0 ) = ∑ i f ( a 0 , i ) − f ( m ) E(t)=E(\phi(A_0))-E(\phi(A_t))=\sum_{i}f(a_{0,i})-f(m)-(n-1)f(0)=\sum_{i}f(a_{0,i})-f(m) E(t)=E(ϕ(A0))−E(ϕ(At))=∑if(a0,i)−f(m)−(n−1)f(0)=∑if(a0,i)−f(m)
这样我们就非常方便的得到了停时的期望
不妨来看一个近一点的例子
杭电多校09 Coins
大意:
n个人,每个人手中初始有 a i a_i ai个硬币,每次随机选择两个人,第一个人给第二个人一个硬币,如果某个人手中没有硬币了,则立即退出游戏,不再回来。当某一个人拥有全部硬币时,游戏结束
问停时的期望
题意与上一题十分相像,但是该题存在人数不固定的情况,所以我们描述游戏局面的时候要稍微改变一下
还是令 m = ∑ a i m=\sum a_i m=∑ai
令 A t = ( a t , 1 , a t , 2 . . . a t , h t ) A_t=(a_{t,1},a_{t,2}...a_{t,h_t}) At=(at,1,at,2...at,ht)来描述第t个时刻的局面,其中 h t h_t ht表示当前的剩余人数,显然它不是一个固定的值。但是我们能保证 ∀ i ≤ h t , a t , i > 0 \forall i\leq h_t,a_{t,i}>0 ∀i≤ht,at,i>0
仿照上一题的思路,我们令 ϕ ( A t ) = ∑ i = 1 n f ( a t , i ) \phi(A_t)=\sum_{i=1}^{n}f(a_{t,i}) ϕ(At)=∑i=1nf(at,i)作为势函数,尝试确定f
E ( ϕ ( A n + 1 ) ∣ A n ) = ∑ i = 1 h t ∑ j ≠ i 1 h t ( h t − 1 ) [ f ( a t , i − 1 ) + f ( a t , j + 1 ) + ∑ k ∉ ( i , j ) f ( a t , k ) ] E(\phi(A_{n+1})|A_n)=\sum_{i=1}^{h_t}\sum_{j\neq i}\frac{1}{h_t(h_t-1)}[f(a_{t,i}-1)+f(a_{t,j}+1)+\sum_{k\notin(i,j)}f(a_{t,k})] E(ϕ(An+1)∣An)=∑i=1ht∑j=iht(ht−1)1[f(at,i−1)+f(at,j+1)+∑k∈/(i,j)f(at,k)]
= ∑ i = 1 h t 1 h t f ( a t , i − 1 ) + 1 h t f ( a t , i + 1 ) + h t h t − 2 f ( a t , i ) =\sum_{i=1}^{h_t}\frac{1}{h_t}f(a_{t,i}-1)+\frac{1}{h_t}f(a_{t,i}+1)+\frac{h_t}{h_t-2}f(a_{t,i}) =∑i=1htht1f(at,i−1)+ht1f(at,i+1)+ht−2htf(at,i)
代入 E ( ϕ ( A n + 1 ) − ϕ ( A n ) ∣ A 0 , A 1 , . . . A n ) = − 1 E(\phi(A_{n+1})-\phi(A_n)|A_0,A_1,...A_n)=-1 E(ϕ(An+1)−ϕ(An)∣A0,A1,...An)=−1,也就是 E ( ϕ ( A n + 1 ) − ϕ ( A n ) ∣ A n ) = − 1 E(\phi(A_{n+1})-\phi(A_n)|A_n)=-1 E(ϕ(An+1)−ϕ(An)∣An)=−1(显然这里当前局面也只与上一个局面有关),有
∑ i = 1 h t f ( a t , i ) = [ ∑ i = 1 h t 1 h t f ( a t , i − 1 ) + 1 h t f ( a t , i + 1 ) + h t h t − 2 f ( a t , i ) ] + 1 \sum_{i=1}^{h_t} f(a_{t,i})=[\sum_{i=1}^{h_t}\frac{1}{h_t}f(a_{t,i}-1)+\frac{1}{h_t}f(a_{t,i}+1)+\frac{h_t}{h_t-2}f(a_{t,i})]+1 ∑i=1htf(at,i)=[∑i=1htht1f(at,i−1)+ht1f(at,i+1)+ht−2htf(at,i)]+1
= ∑ i = 1 h t ( 1 h t f ( a t , i − 1 ) + 1 h t f ( a t , i + 1 ) + h t h t − 2 f ( a t , i ) + 1 h t ) =\sum_{i=1}^{h_t}(\frac{1}{h_t}f(a_{t,i}-1)+\frac{1}{h_t}f(a_{t,i}+1)+\frac{h_t}{h_t-2}f(a_{t,i})+\frac{1}{h_t}) =∑i=1ht(ht1f(at,i−1)+ht1f(at,i+1)+ht−2htf(at,i)+ht1)
抽象出 f ( a ) = 1 h f ( a − 1 ) + 1 h f ( a + 1 ) + h h − 2 f ( a ) + 1 h f(a)=\frac{1}{h}f(a-1)+\frac{1}{h}f(a+1)+\frac{h}{h-2}f(a)+\frac{1}{h} f(a)=h1f(a−1)+h1f(a+1)+h−2hf(a)+h1
f ( a + 1 ) − f ( a ) = f ( a ) − f ( a − 1 ) − 1 f(a+1)-f(a)=f(a)-f(a-1)-1 f(a+1)−f(a)=f(a)−f(a−1)−1
令 g ( a ) = f ( a ) − f ( a − 1 ) , 有 g ( a ) = g ( 0 ) − a g(a)=f(a)-f(a-1),有g(a)=g(0)-a g(a)=f(a)−f(a−1),有g(a)=g(0)−a,则 f ( a ) = f ( 0 ) + a g ( 0 ) − a ( a + 1 ) 2 f(a)=f(0)+ag(0)-\frac{a(a+1)}{2} f(a)=f(0)+ag(0)−2a(a+1)
取 f ( 0 ) = g ( 0 ) = 0 f(0)=g(0)=0 f(0)=g(0)=0,则 f ( a ) = − a ( a + 1 ) 2 f(a)=-\frac{a(a+1)}{2} f(a)=−2a(a+1)
所以 E ( t ) = E ( ϕ ( A 0 ) ) − E ( ϕ ( A t ) ) = ∑ i = 1 n f ( a 0 , i ) − f ( m ) E(t)=E(\phi(A_0))-E(\phi(A_t))=\sum_{i=1}^{n}f(a_{0,i})-f(m) E(t)=E(ϕ(A0))−E(ϕ(At))=∑i=1nf(a0,i)−f(m)
未完待续
相关文章:

势函数和鞅的停时定理
前置芝士 鞅: 鞅是一类特殊的随机过程,假设我们从一开始就在观察一场赌博游戏,现在已经得到了前t秒的观测值,那么当第t1 秒观测值的期望等于第t秒的观测值时,我们称这是一个公平赌博游戏。 具体来说,对于…...

途乐证券-炒股开户流程是怎样的?
炒股是一种危险较大但收益也相对较高的出资方法,而开户则是出资炒股的前提。跟着科技的开展,炒股开户已经能够在线完结,但流程相对来说仍是比较繁琐的。那么,炒股开户流程是怎样的呢?下面从多个视点剖析。 一、炒股开户…...
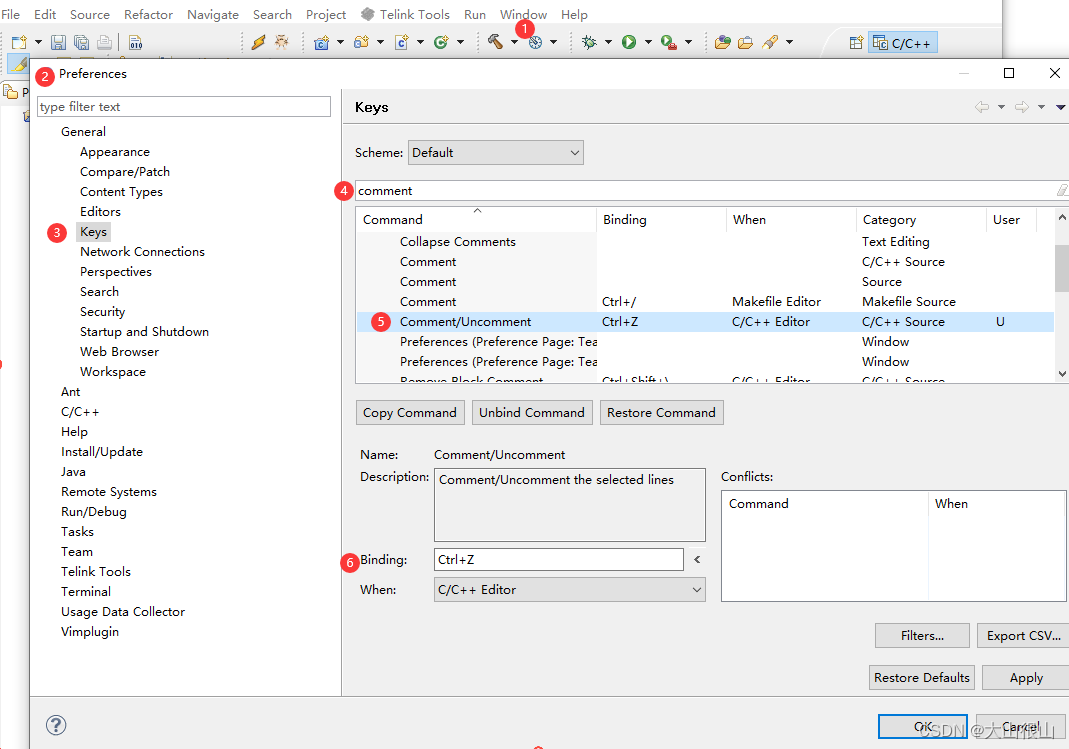
Eclipse如何设置快捷键
在eclopse设置注释行和取消注释行 // 打开eclipse,依次打开:Window -> Preferences -> General -> Key,...

刷享全球美好 中信银行信用卡推出跨境消费系列活动
来源 | 镭射财经(leishecaijing) 日前,文旅部办公厅发布通知,恢复全国旅行社及在线旅游企业经营中国公民赴有关国家和地区(第三批)出境团队旅游和“机票酒店”业务,出境跟团游国家和地区由此前…...

LeetCode算法心得——限制条件下元素之间的最小绝对差(TreeSet)
大家好,我是晴天学长,今天用到了Java一个非常实用的类TreeSet,能解决一些看起来棘手的问题。 1 )限制条件下元素之间的最小绝对差 2) .算法思路 初始化变量:n为列表nums的大小。 min为整型最大值,用于记录…...
)
MySQL表的基础操作(crud)
1. 新增(Create) insert into 表名 values (值, 值…); 此处列出的这些值,的数目和类型要和表的列相匹配。 -- 在student 表中插入学号1,姓名zhangsan的数据 insert into student values(1, zhangsan); -- 指定列插入 insert into student …...

vue中的activated和deactivated
目录 一、简介二、使用 一、简介 当页面被keep-alive缓存下来的时候,vue提供两个钩子函数 activated被 keep-alive 缓存的组件激活时调用。deactivated被 keep-alive 缓存的组件失活时调用。 当keepalive页面缓存,有activated钩子和created钩子函数时 …...

unity 发布报错 The type or namespace name `UnityEditor‘ could not be found.
引用了UnityEditor的内容,发布当然会报错啦 加上宏判断就好啦...
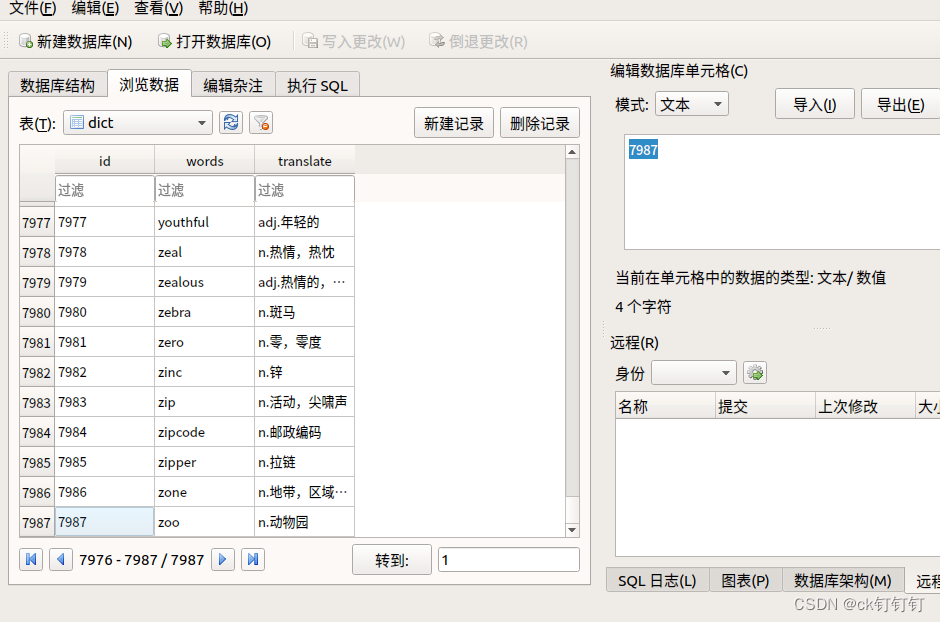
在ubuntu中将dict.txt导入到数据库sqlite3
将dict.txt导入到数据库 #include <head.h> #include <sqlite3.h> int do_insert(int i,char *str,sqlite3 *db); int main(int argc, const char *argv[]) {//创建泵打开一个数据库sqlite3 *db NULL;if(sqlite3_open("./my.db",&db) ! SQLITE_OK){…...

nginx 代理postgresql
首先,Nginx为我们的数据库增加了额外的安全层。Nginx提供了一整套的选项,这使得管理访问和保护数据库变得很容易。例如,我们可以配置为只有一小部分IP地址可以访问数据库。 PostgreSQL不使用HTTP或HTTPS,而是使用一个新块儿strea…...

小程序 CSS-in-JS 和原子化的另一种选择
小程序 CSS-in-JS 和原子化的另一种选择 小程序 CSS-in-JS 和原子化的另一种选择 介绍快速开始 pandacss 安装和配置 0. 安装和初始化 pandacss1. 配置 postcss2. 检查你的 panda.config.ts3. 修改 package.json 脚本4. 全局 css 注册 pandacss5. 配置的优化与别名 weapp-pand…...

flutter项目 环境搭建
开发flutter项目 搭建工具环境 flutter项目本身 所需开发工具环境 flutter 谷歌公司开发 系统支持库 镜像库 搭建流程: flutter 官网: https://flutter.dev/community/china //步骤1 .bash_profile touch .bash_profile pwd /Users/haijunyan open ~ e…...

PG-DBA培训12:PostgreSQL物理备份与恢复实战
一、风哥PG-DBA培训12:PostgreSQL物理备份与恢复实战 课程目标: 本课程由风哥发布的基于PostgreSQL数据库的系列课程,本课程属于PostgreSQL备份恢复与迁移升级阶段之PostgreSQL物理备份与恢复实战,学完本课程可以掌握࿱…...
饿了么大数据开发凉经
1 一个mapreduce进程会启动多少map进程多少reduce进程* 1)map数量由处理的数据分成的block数量决定default_num total_size / split_size; 2)reduce数量为job.setNumReduceTasks(x)中x 的大小。不设置的话默认为 1。 2 讲下shuffle的过程 shuffle分为…...

前端安全:XSS 与 CSRF 安全防御
在当今数字化的时代,前端安全性变得愈发重要。跨站脚本攻击(XSS)和跨站请求伪造(CSRF)是常见的前端安全威胁,但通过一些简单的防御策略,我们可以有效地保护我们的应用程序和用户信息。本文将为您…...

应用层读取wfp防火墙阻断记录
前言 之前的文档中,描写了如何对WFP防火墙进行操作[链接在此],这篇文档中,描述如何获取WFP防火墙进行阻断的操作记录。 需要注意的坑点 使用FWPM_NET_EVENT_TYPE获取防火墙日志时,需要注意,只有丢弃和内核丢弃&…...
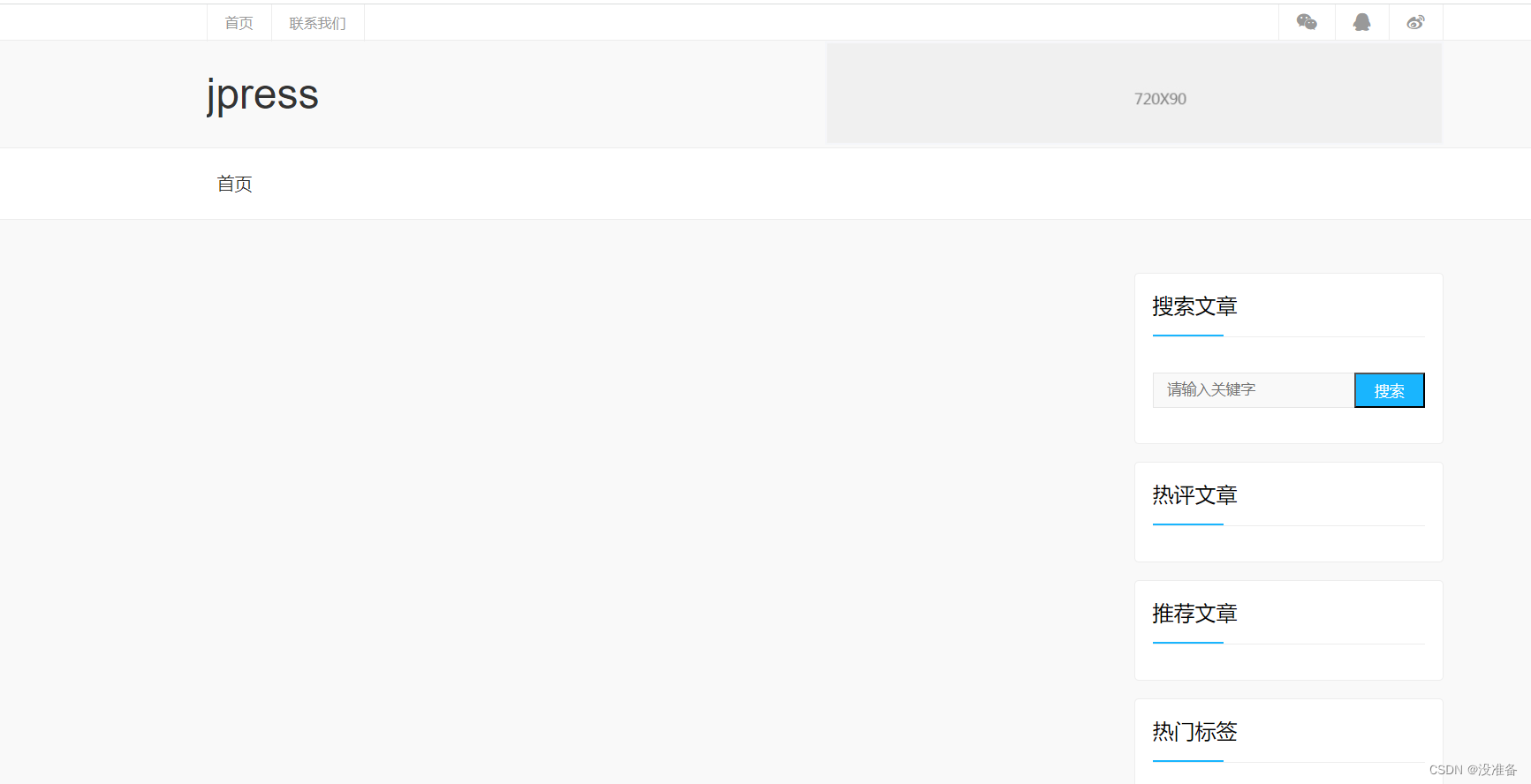
web基础和tomcat的安装,部署jpress应用
目录 1. 简述静态网页和动态网页的区别。 2. 简述 Webl.0 和 Web2.0 的区别。 3. 安装tomcat8,配置服务启动脚本,部署jpress应用。 1. 简述静态网页和动态网页的区别。 【1】定义区别 请求响应信息,发给客户端进行处理,由浏览…...
idea git命令使用
这个标签标识单签分支:(标签图标) 标识关联分支:(五角星) 本地切换分支:如当前分支是dev ,git branch 显示的是dev ,然后通过 git checkout -b release 切换到release分支 git checkout re…...

软件测试技术之单元测试—工程师 Style 的测试方法
什么是单元测试? Wikipedia 对单元测试的定义: 在计算机编程中,单元测试(Unit Testing)又称为模块测试,是针对程序模块(软件设计的最小单位)来进行正确性检验的测试工作。 在实际…...

C#学习....
1.基础 //引用命名空间using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks;//项目名或者命名空间 namespace _01_MY_First_Demo {//Program类class Program{//程序的主入口或者Main函数static void Main(S…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...
