【笔记】优先队列(priority_queue/set)
目录
大根堆
小根堆
set(小根堆)
大根堆
题目链接:洛谷 P3243 菜肴制作
题目描述
知名美食家小 A 被邀请至 ATM 大酒店,为其品评菜肴。ATM 酒店为小 A 准备了 n 道菜肴,酒店按照为菜肴预估的质量从高到低给予 1 到 n 的顺序编号,预估质量最高的菜肴编号为 1。
由于菜肴之间口味搭配的问题,某些菜肴必须在另一些菜肴之前制作,具体的,一共有 m 条形如 i 号菜肴必须先于 j 号菜肴制作的限制,我们将这样的限制简写为 (i,j)。
现在,酒店希望能求出一个最优的菜肴的制作顺序,使得小 A 能尽量先吃到质量高的菜肴:
也就是说,
-
在满足所有限制的前提下,1 号菜肴尽量优先制作。
-
在满足所有限制,1 号菜肴尽量优先制作的前提下,2 号菜肴尽量优先制作。
-
在满足所有限制,1 号和 22 号菜肴尽量优先的前提下,3 号菜肴尽量优先制作。
-
在满足所有限制,1 号和 2 号和 3 号菜肴尽量优先的前提下,4 号菜肴尽量优先制作。
-
以此类推。
例 1:共 4 道菜肴,两条限制 (3,1)、(4,1),那么制作顺序是 3,4,1,2。
例 2:共 5 道菜肴,两条限制 (5,2)、(4,3),那么制作顺序是 1,5,2,4,3。
例 1 里,首先考虑 1,因为有限制 (3,1) 和 (4,1),所以只有制作完 3 和 4 后才能制作 1,而根据 3,3 号又应尽量比 4 号优先,所以当前可确定前三道菜的制作顺序是 3,4,1;接下来考虑 2,确定最终的制作顺序是 3,4,1,2。
例 2 里,首先制作 1 是不违背限制的;接下来考虑 2 时有 (5,2) 的限制,所以接下来先制作 55 再制作 2;接下来考虑 3 时有 (4,3) 的限制,所以接下来先制作 4 再制作 3,从而最终的顺序是 1,5,2,4,3。现在你需要求出这个最优的菜肴制作顺序。无解输出 Impossible!(首字母大写,其余字母小写)
输入格式
第一行是一个正整数 t,表示数据组数。接下来是 t 组数据。对于每组数据:第一行两个用空格分开的正整数 n 和 m,分别表示菜肴数目和制作顺序限制的条目数。接下来 m 行,每行两个正整数 x,y,表示 x 号菜肴必须先于 y 号菜肴制作的限制。
输出格式
输出文件仅包含 t 行,每行 n 个整数,表示最优的菜肴制作顺序,或者 Impossible! 表示无解。
输入输出样例
输入 #1复制
3 5 4 5 4 5 3 4 2 3 2 3 3 1 2 2 3 3 1 5 2 5 2 4 3
输出 #1复制
1 5 3 4 2 Impossible! 1 5 2 4 3
说明/提示
【样例解释】
第二组数据同时要求菜肴 1 先于菜肴 2 制作,菜肴 2 先于菜肴 3 制作,菜肴 3 先于。
菜肴 1 制作,而这是无论如何也不可能满足的,从而导致无解。
【数据范围】
100% 的数据满足 n,m≤105,1≤t≤3。
m 条限制中可能存在完全相同的限制。
思想:用大根堆不用小根堆的原因,用小根堆只能找到小点,但是无法保证能先选到1在前面的点,比如4 2,5 1,那么小根堆会优先选择4 2,这样的排列顺序不符合题意,要想1出现在前面,那么可以反向建边,用大根堆,这样的排列顺序就是5 1,最后再翻转输出就可以了。
代码
// Problem: D - 菜肴制作
// Contest: Virtual Judge - 2023暑期训练-图论part1
// URL: https://vjudge.net/contest/574296#problem/D
// Memory Limit: 128 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include<bits/stdc++.h>
using namespace std;typedef long long ll;const int N = 2e5+5;int n,m;
int in[N];
vector<int> edge[N];
vector<int> ans;void toposort(){priority_queue<int> q;//q.clear();for(int i=1;i<=n;i++){if(in[i]==0){q.push(i);}}while(!q.empty()){int t=q.top();q.pop();ans.push_back(t);for(int i=0;i<edge[t].size();i++){in[edge[t][i]]--;if(in[edge[t][i]]==0){q.push(edge[t][i]);}}}if(ans.size()<n){cout<<"Impossible!"<<"\n";}else{for(int i=n-1;i>=0;i--){cout<<ans[i]<<' ';}cout<<"\n";}}int main(){int T;cin>>T;while(T--){cin>>n>>m;ans.clear();memset(in,0,N);for(int i=0;i<N;i++){edge[i].clear();}for(int i=1;i<=m;i++){int x,y;cin>>x>>y;edge[y].push_back(x);in[x]++;}toposort();}return 0; }
题目链接:代码源 最短路
给你一张 n 个顶点 m 条边的有向简单图,顶点编号从 1 到 n,每条边都有一个边权,边权为非负整数。
现在有 k 组询问,每组询问读入两个整数 x,y,请求出从 x 号点到 y 号点的最短路的长度。如果不存在从 x 号点到 y 号点的路径,请输出 -1。
输入格式
第一行三个整数 n,m,k,表示图的顶点数、边数和询问次数。
接下来 m 行,每行三个整数 x,y,z,表示 x𝑥 号点到 y 号点有一条边权为 z 的有向边。
接下来 k 行,每行两个整数 x,y,表示一组询问。
输出格式
输出共 k 行,每行一个数表示一组询问的答案。
样例输入
3 3 2
1 2 3
2 3 2
3 2 1
1 3
3 1样例输出
5
-1数据规模
对于所有数据,保证 2≤n≤5000,0≤m≤10000,1≤k≤5,1≤x,y≤n,1≤z≤10000。
思想:set是一种数据结构,可以维护数据按照从小到大的顺序排列
小根堆
priority_queue<pii,vector<pii>,greater<pii>> q;
#include<bits/stdc++.h>
using namespace std;typedef long long ll;
typedef pair<int,int> pii;const int N = 2e5+5;struct node{int y,v; //连接的边以及边权node(int _y,int _v){y=_y;v=_v;}
};vector<node> edge[N+1];
int dist[N+1];
int n,m,k;
priority_queue<pii,vector<pii>,greater<pii>> q;
bool st[N];void dijkstra(int s,int t){memset(dist,127,N+1);memset(st,false,N);dist[s]=0;//q.clear();for(int i=1;i<=n;i++){q.push({dist[i],i});}while(!q.empty()){int x=q.top().second;q.pop();if(st[x]) continue;st[x]=true;for(auto i:edge[x]){if(dist[x]+i.v<dist[i.y]){dist[i.y]=dist[x]+i.v;q.push({dist[i.y],i.y});}}}if(dist[t]<1<<30){cout<<dist[t]<<"\n";}else{cout<<"-1\n";}}int main(){cin>>n>>m>>k;for(int i=1;i<=m;i++){int x,y,z;cin>>x>>y>>z;edge[x].push_back(node(y,z));}for(int i=1;i<=k;i++){int s,t;cin>>s>>t;dijkstra(s,t);}return 0; }set(小根堆)
#include<bits/stdc++.h>
using namespace std;typedef long long ll;
typedef pair<int,int> pii;const int N = 2e5+5;struct node{int y,v; //连接的边以及边权node(int _y,int _v){y=_y;v=_v;}
};vector<node> edge[N+1];
int dist[N+1];
int n,m,k;
set<pii> se;void dijkstra(int s,int t){memset(dist,127,N+1);dist[s]=0;se.clear();for(int i=1;i<=n;i++){se.insert({dist[i],i});}while(!se.empty()){int x=se.begin()->second;if(x==t||dist[x]>1<<30){break;}se.erase(se.begin());for(auto i:edge[x]){if(dist[x]+i.v<dist[i.y]){se.erase({dist[i.y],i.y});dist[i.y]=dist[x]+i.v;se.insert({dist[i.y],i.y});}}}if(dist[t]<1<<30){cout<<dist[t]<<"\n";}else{cout<<"-1\n";}}int main(){cin>>n>>m>>k;for(int i=1;i<=m;i++){int x,y,z;cin>>x>>y>>z;edge[x].push_back(node(y,z));}for(int i=1;i<=k;i++){int s,t;cin>>s>>t;dijkstra(s,t);}return 0; }相关文章:
)
【笔记】优先队列(priority_queue/set)
目录 大根堆 小根堆 set(小根堆) 大根堆 题目链接:洛谷 P3243 菜肴制作 题目描述 知名美食家小 A 被邀请至 ATM 大酒店,为其品评菜肴。ATM 酒店为小 A 准备了 n 道菜肴,酒店按照为菜肴预估的质量从高到低给予 1 到…...
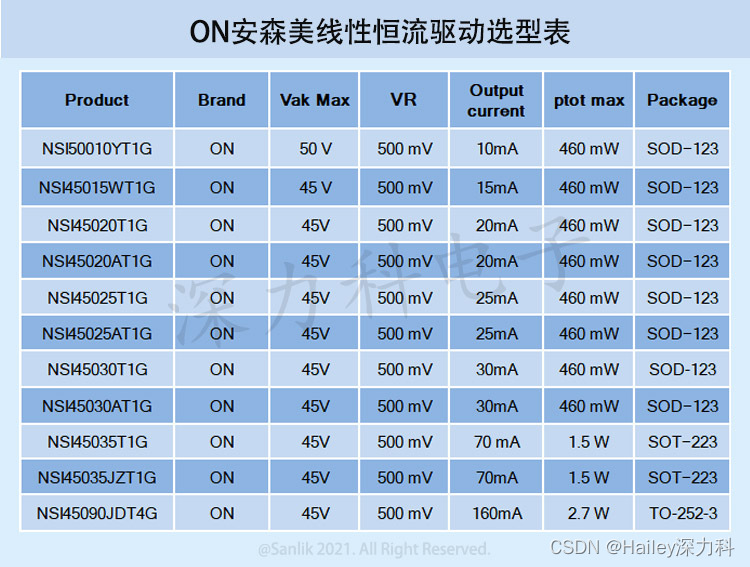
看看安森美深力科NSI45090JDT4G 是如何点亮汽车内外照明系统解决方案
关于线性恒流调节器(CCR):是一种用于控制电流的稳定输出。它通常由一个功率晶体管和一个参考电流源组成。CCR的工作原理是通过不断调节功率晶体管的导通时间来维持输出电流的恒定。当输出电流超过设定值时,CCR会减少功率晶体管的导…...

Linux进阶之Shell-sed
基本用法: sed 选项 “指令” 文件 常用选项: -e --它告诉sed将下一个参数解释为一个sed指令,只有当命令行上给出多个sed指令时使用 -f --后跟保存了sed指令的文件 -i --直接对内容进行修改,不加 i 时默认只是预…...

前端高频面试题 Day02
面试题 var 和 let const 的区别 var 是 ES5 及之前的语法,let const 是 ES6 语法var 和 let 是变量,可修改;const 是常量,不可修改var 有变量提升,let const 没有var 没有块级作用域,let const 有 &…...
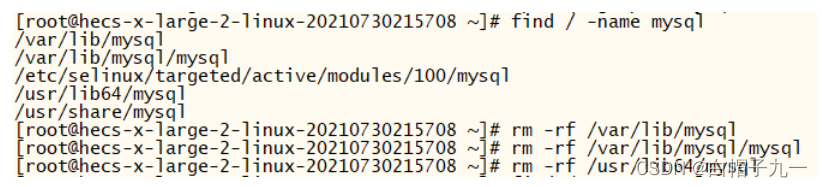
MYSQL完全卸载、安装与账号创建、权限控制
一、卸载mysql CentOS 卸载 MySQL 1. 查看安装情况 使用以下命令查看当前安装mysql情况,查找以前是否装有mysql rpm -qa|grep -i mysql这里显示我安装的 MySQL 服务有有: 2. 停止 mysql 服务、删除之前安装的 mysql 删除命令:rpm -e –n…...

get与post如何拼接url与数据的灵活处理,循环的重要性。
get与post拼接url地址不同: let postData {method: "post",data: {op: "/api/setting/maintenanceperiod?period"this.authorizationCode,loadingConfig: {},data: {period:this.authorizationCode}}}; if(this.editData.id){let postData …...
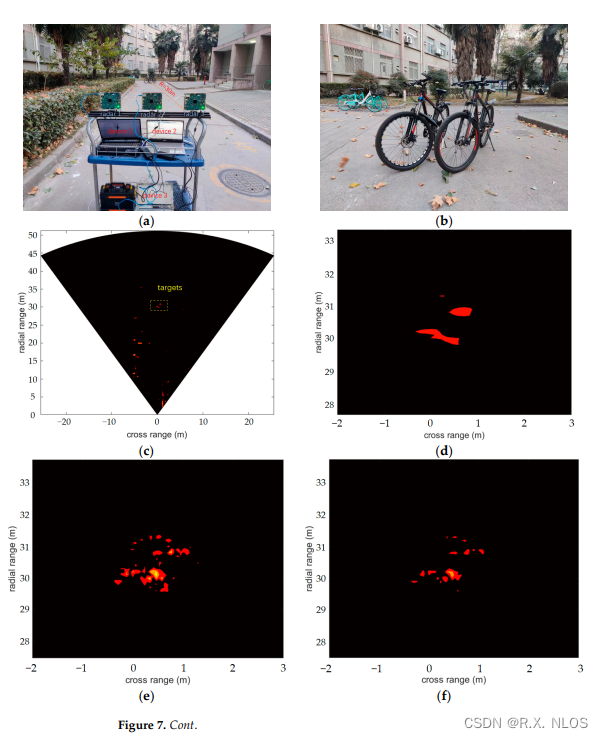
Remote Sensing,2023 | 基于SBL的分布式毫米波相干雷达成像的高效实现
Remote Sensing,2023 | 基于SBL的分布式毫米波相干雷达成像的高效实现 注1:本文系“无线感知论文速递”系列之一,致力于简洁清晰完整地介绍、解读无线感知领域最新的顶会/顶刊论文(包括但不限于 Nature/Science及其子刊; MobiCom, Sigcom, MobiSys, NSDI…...

Android学习之路(5) UI控件之Button (按钮)与 ImageButton (图像按钮)
本节引言: 今天给大家介绍的Android基本控件中的两个按钮控件,Button普通按钮和ImageButton图像按钮; 其实ImageButton和Button的用法基本类似,至于与图片相关的则和后面ImageView相同,所以本节 只对Button进行讲解&am…...
)
Day 31 C++ STL常用算法(下)
文章目录 常用拷贝和替换算法copy——容器内指定范围的元素拷贝到另一容器中函数原型注意——利用copy算法在拷贝时,目标容器要提前开辟空间示例 replace——将容器内指定范围的第一个旧元素修改为新元素函数原型注意——replace只会替换区间内满足条件的第一个旧元…...

【Android Studio】 win11 安装配置 jdk17 超详细
概述 一个好的安装教程能够帮助开发者完成更便捷、更快速的开发。书山有路勤为径,学海无涯苦作舟。我是秋知叶i、期望每一个阅读了我的文章的开发者都能够有所成长。 一、下载JDK JDK官网 这里下载 JDK17 windows x64 installer 二、安装JDK 双击打开下载的 j…...
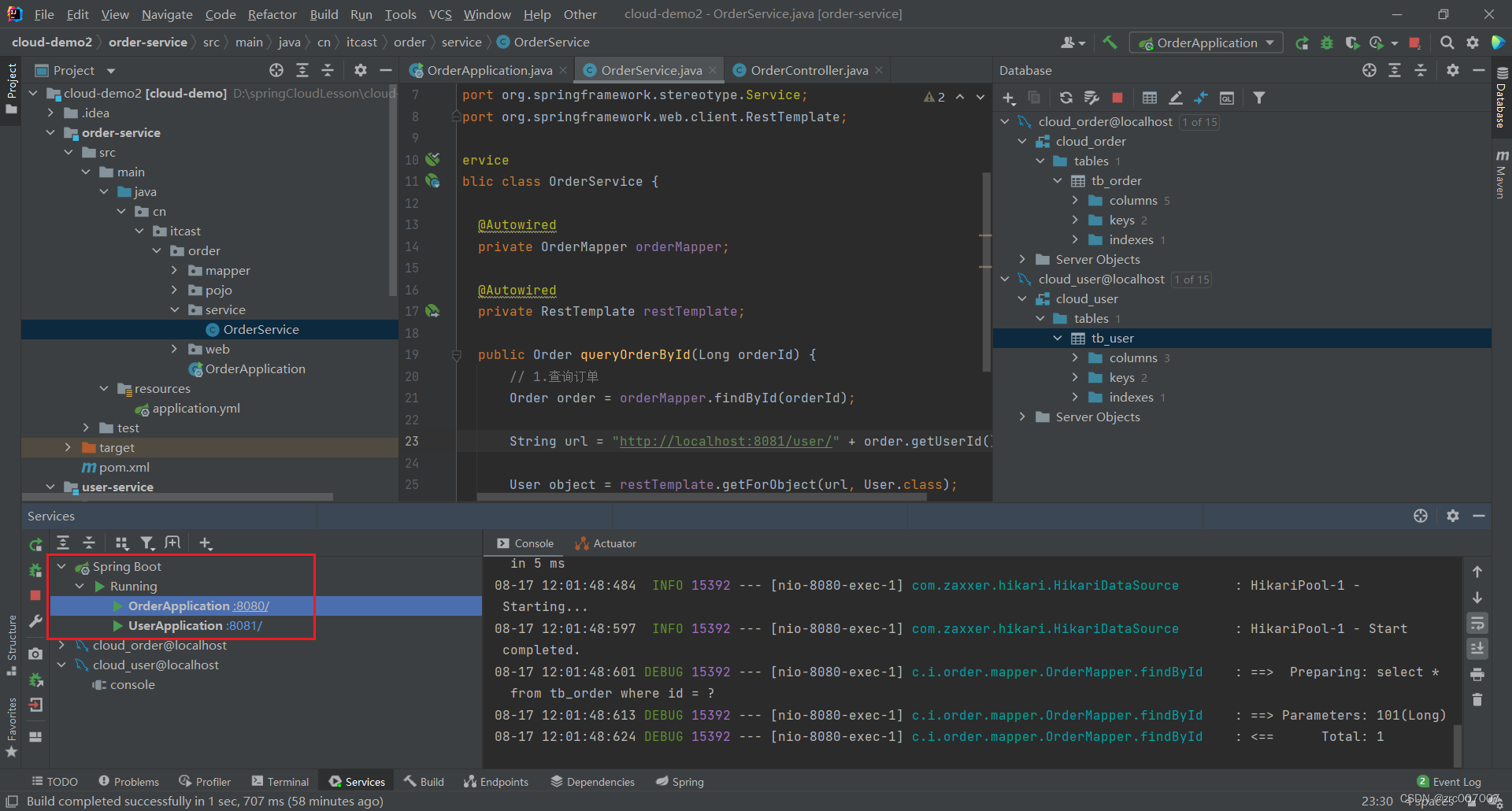
IDEA下方工具栏SideBar没有Services解决方法 IDEA配合微服务学习多端口管理打开Services栏方法
问题 微服务学习时,一次要打开多个端口,比如8080给order模块、8081给user模块……这就需要用idea管理多端口。 这时候就可以用到Services栏进行管理。 解决 首先看下方Sidebar没有Services。 打开Services 打开方式一:手动打开 在IDEA中…...

[Vue warn]: Error in render: “SyntaxError: “undefined“ is not valid JSON“
[Vue warn]: Error in render: “SyntaxError: “undefined” is not valid JSON” 这说明出现了undefined这个变量类型,比如JSON.parse()时候会出现,可以先尝试打印JSON.parse()括号中的内容是否是undefined,如果是,那问题的根源…...

ui设计师工作总结及计划范文模板
ui设计师工作总结及计划范文模板【篇一】 白驹过隙,转眼间某某年已近结尾,时间伴随着我们的脚步急驰而去,到了个人工作总结的时候,蓦然回首,才发现过去的一年不还能画上圆满的句号,内心感慨万千,…...
【Kafka】2.在SpringBoot中使用官方原生java版Kafka客户端
目 录 1. 新建一个消息生产者2. 新建一个消息消费者3. 测 试 在开始之前,需要先做点准备工作,用 IDEA 新建一个 Maven 项目,取名 kafka-study,然后删掉它的 src 目录,接着在 pom.xml 里面引入下面的依赖。这个项目的作…...
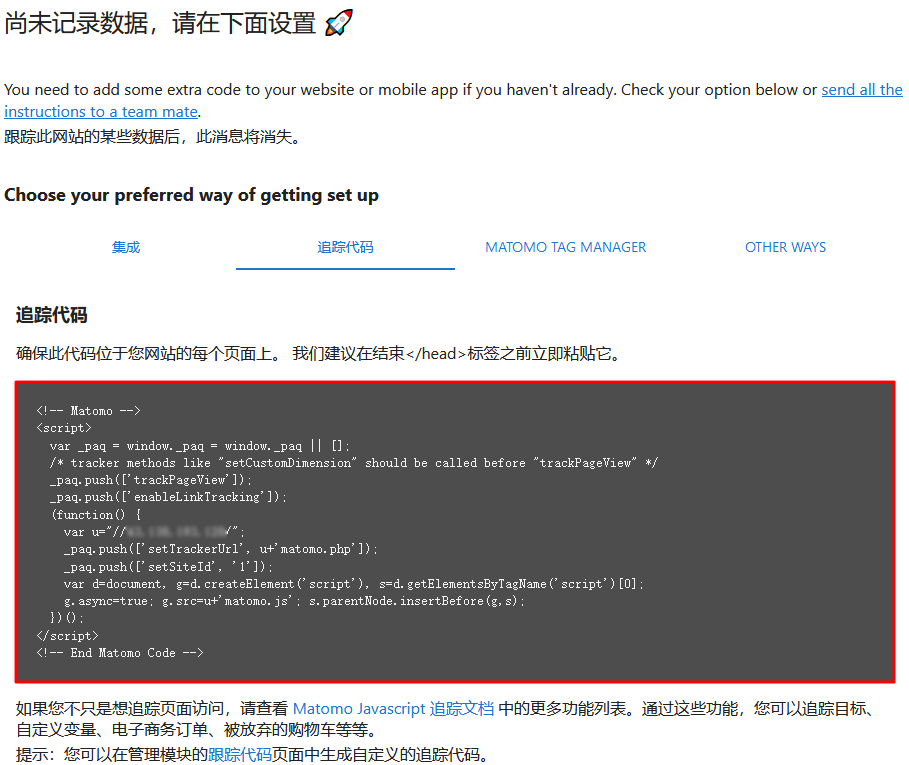
使用腾讯云轻量服务器Matomo应用模板建网站流量统计系统
腾讯云百科分享使用腾讯云轻量应用服务器Matomo应用模板搭建网站流量统计系统,Matomo 是一款开源的网站数据统计软件,可以用于跟踪、分析您的网站的流量,同时充分保障数据安全性、隐私性。该镜像基于 CentOS 7.6 64位操作系统,已预…...
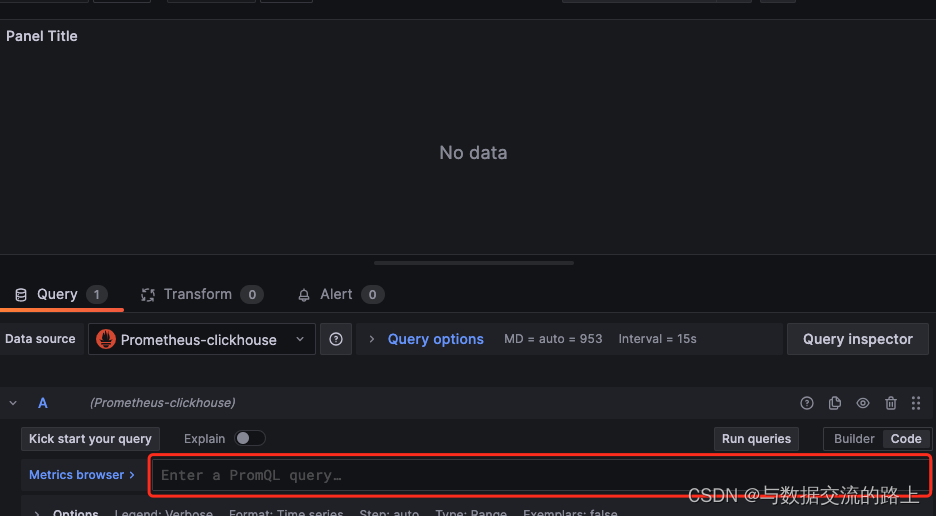
clickhouse-监控配置
一、概述 监控是运维的一大利器,要想运维好clickhouse,首先就要对其进行监控,clickhouse有几种监控数据的方式,一种是系统本身监控,一种是通过exporter来监控,下面分别描述一下 二、系统自带监控 我下面会对监控做一…...
互斥量概念、用法、死锁演示及解决详解)
C++11并发与多线程笔记(5)互斥量概念、用法、死锁演示及解决详解
C11并发与多线程笔记(5)互斥量概念、用法、死锁演示及解决详解 1、互斥量(mutex)的基本概念2、互斥量的用法2.1 lock(),unlock()2.2 lock_guard类模板 3、死锁3.1 死锁演示3.2 死锁的一般解决方案:3.3 std:…...
华为云classroom赋能--Devstar使应用开发无需从零开始
华为云DevStar为开发者提供业界主流框架代码初始化能力,通过GUI、API、CLI等多种方式,将按模板生成框架代码的能力推送至用户桌面。同时基于华为云服务资源、成熟的DevOps开发工具链和面向多场景的众多开发模板,提供一站式创建代码仓、自动生…...

软件的数据回滚
原理:所谓的数据回滚,就是数据备份 增量备份: 全量备份: 最简单的事全量备份。 就是spoon工具,完成把所有的表每天定时复制一份,表名“_日期”。 所以有实时表,每日备份表。 回滚就是把之前…...

git clone使用https协议报错OpenSSL SSL_read: Connection was reset, errno 10054
在使用git 下载github上的代码时, 一般有ssh协议和https协议两种。使用ssh协议可以成功clone代码, 但使用https协议时出错: $ git clone https://github.com/openai/improved-diffusion.git Cloning into improved-diffusion... fatal: unab…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...
