Remote Sensing,2023 | 基于SBL的分布式毫米波相干雷达成像的高效实现
Remote Sensing,2023 | 基于SBL的分布式毫米波相干雷达成像的高效实现
注1:本文系“无线感知论文速递”系列之一,致力于简洁清晰完整地介绍、解读无线感知领域最新的顶会/顶刊论文(包括但不限于 Nature/Science及其子刊; MobiCom, Sigcom, MobiSys, NSDI, SenSys, Ubicomp; JSAC, 雷达学报 等)。
本次介绍的论文是:2023,Remote Sensing | Efficient Implementation for SBL-Based Coherent Distributed mmWave Radar Imaging
文章DOI: https://doi.org/10.3390/rs15041054
文章动机
毫米波雷达因其小型化、高分辨率、长距离探测等优点,在汽车自动驾驶、交通监测、无人机避障等民用领域得到广泛应用。但是,单雷达的角分辨率有限,难以满足实际需求。本文提出在多个分布式小孔径毫米波雷达之间实现相干合成,通过信号处理算法提高雷达系统的有效孔径,从而改善角分辨率。
但是传统的距离多普勒成像算法,在错位数据情况下效果较差。而稀疏贝叶斯学习(SBL)算法由于鲁棒性强、精度高,适合处理探测数据不连续的情况,可以用于分布式雷达成像。但是SBL算法计算复杂度高。
因此,本文针对FMCW雷达的数据结构特点,提出一种快速SBL算法,名称为LC-SBL,可以大幅降低算法计算复杂度。该算法对增强分布式毫米波雷达的角分辨率具有重要意义。

文章思路
-
引言部分概述文章研究背景、问题和方法。
-
第二部分介绍分布式FMCW MIMO雷达系统模型,以及SBL算法原理。
-
第三部分是文章的核心贡献部分。介绍针对雷达数据的特点,提出一种TBT矩阵求逆的新分解方法。并基于该分解提出LC-SBL快速算法,可以利用FFT快速计算。
-
第四部分是仿真验证和实验结果。分别用仿真数据和实际测量数据验证LC-SBL算法在改进角分辨率和降低计算复杂度方面的优势。
-
最后是结论部分,总结全文的贡献。
好的,我继续完成博客文章的撰写:
LC-SBL算法的技术原理
LC-SBL算法的核心创新点是提出一种TBT矩阵逆矩阵的新分解方法。
在雷达成像问题中,采集到的回波信号r和成像结果u之间的关系可以表示为:
r = H u + η r=Hu+\eta r=Hu+η
其中 H H H是采样矩阵,可以表示为傅立叶字典矩阵的形式。这样 H H H对应的协方差矩阵是一个TBT矩阵:
F = H Λ H H F=H\Lambda H^H F=HΛHH
TBT矩阵具有Toeplitz块圈矩阵的结构特点,如公式(15)所示。
为了快速求解u,需要对矩阵 Q = I + β F Q=I+\beta F Q=I+βF进行求逆运算。文章提出了一种新颖的TBT矩阵逆矩阵的分解方法:
将Q的逆矩阵表示为下三角Toeplitz块矩阵 L ( x ) L(x) L(x)和圈矩阵 C ( J μ ) C(J\mu) C(Jμ)之积的和,具体如公式(40)所示。
Q − 1 = L ( x ) C ( J μ ‾ ) − ( L ( μ ) − I ) C ( J x ‾ ) = L ( x ) C ( J μ ‾ ) − L ( μ − E 0 ) C ( J x ‾ ) \begin{aligned} \mathbf{Q}^{-1} & =\mathrm{L}(\mathbf{x}) C(\mathbf{J} \overline{\boldsymbol{\mu}})-(\mathrm{L}(\boldsymbol{\mu})-\mathbf{I}) \mathrm{C}(\mathbf{J} \overline{\mathbf{x}}) \\ & =\mathrm{L}(\mathbf{x}) \mathrm{C}(\mathbf{J} \overline{\boldsymbol{\mu}})-\mathrm{L}\left(\boldsymbol{\mu}-\mathbf{E}_0\right) \mathrm{C}(\mathbf{J} \overline{\mathbf{x}})\end{aligned} Q−1=L(x)C(Jμ)−(L(μ)−I)C(Jx)=L(x)C(Jμ)−L(μ−E0)C(Jx)
这样,原来需要大量计算的矩阵求逆运算,可以转换为三角Toeplitz矩阵的线性卷积,和圈矩阵的圈卷积。这两种运算可以通过FFT快速实现。
因此,文章提出的LC-SBL算法,可以将SBL中大部分时间耗费的运算,转换为FFT运算,从而大幅降低算法复杂度。
仿真与实验结果
为验证LC-SBL算法的优势,文章进行了仿真和实验对比。
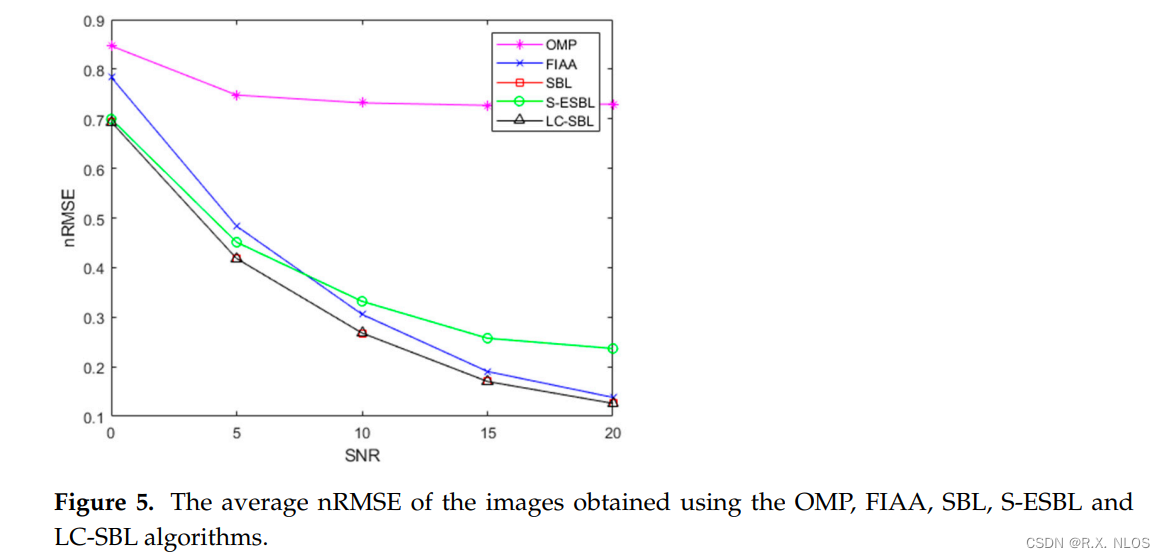
仿真方面,与FIAA、OMP、S-ESBL等算法进行比较,结果如图5所示。LC-SBL的重构误差最小,运行时间也是最短的。
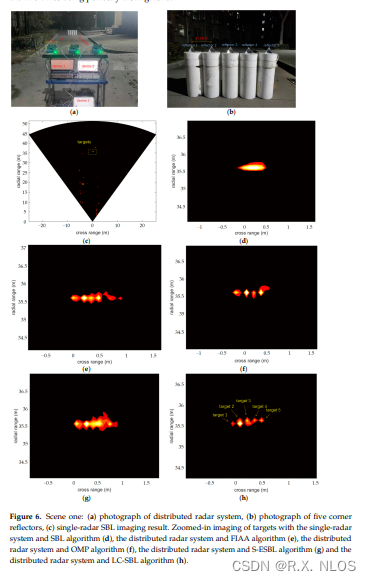
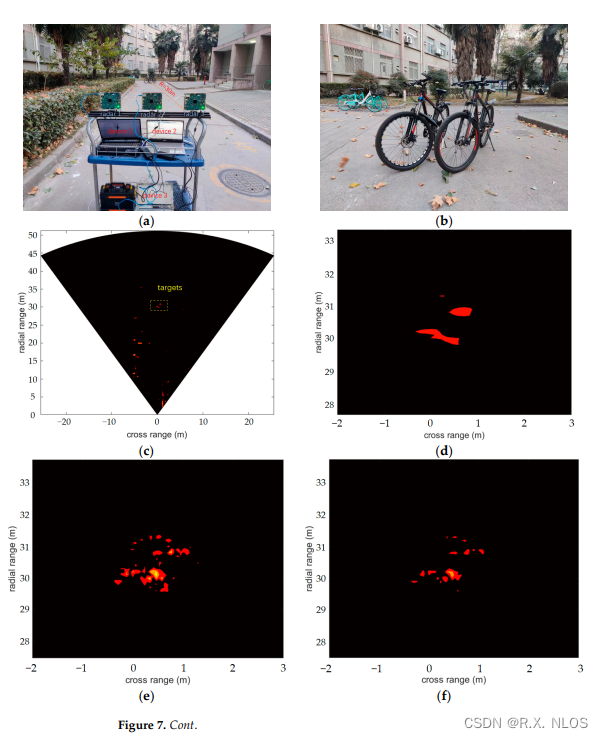
实验部分,构建了一个三雷达的分布式毫米波雷达系统,对比单雷达系统和分布式雷达系统的成像效果。如图6和图7所示,在成像分辨率方面,LC-SBL优于FIAA、OMP、S-ESBL等算法。可以成功识别单雷达系统无法识别的多个目标。
总结与展望
- 本文针对分布式毫米波雷达成像问题,提出一种LC-SBL快速算法。其基于TBT矩阵的新分解思想,可以将大量计算转化为FFT运算,从而大幅降低SBL算法的计算复杂度。
- 仿真和实验结果表明,LC-SBL算法不仅计算效率高,也使分布式雷达系统获得了与大孔径雷达相当的高角分辨率。
- 未来可考虑在LC-SBL算法框架下,引入更多针对雷达任务的先验知识,如目标稀疏性、形状特征等,可望获得更好的成像效果。
相关文章:

Remote Sensing,2023 | 基于SBL的分布式毫米波相干雷达成像的高效实现
Remote Sensing,2023 | 基于SBL的分布式毫米波相干雷达成像的高效实现 注1:本文系“无线感知论文速递”系列之一,致力于简洁清晰完整地介绍、解读无线感知领域最新的顶会/顶刊论文(包括但不限于 Nature/Science及其子刊; MobiCom, Sigcom, MobiSys, NSDI…...

Android学习之路(5) UI控件之Button (按钮)与 ImageButton (图像按钮)
本节引言: 今天给大家介绍的Android基本控件中的两个按钮控件,Button普通按钮和ImageButton图像按钮; 其实ImageButton和Button的用法基本类似,至于与图片相关的则和后面ImageView相同,所以本节 只对Button进行讲解&am…...
)
Day 31 C++ STL常用算法(下)
文章目录 常用拷贝和替换算法copy——容器内指定范围的元素拷贝到另一容器中函数原型注意——利用copy算法在拷贝时,目标容器要提前开辟空间示例 replace——将容器内指定范围的第一个旧元素修改为新元素函数原型注意——replace只会替换区间内满足条件的第一个旧元…...

【Android Studio】 win11 安装配置 jdk17 超详细
概述 一个好的安装教程能够帮助开发者完成更便捷、更快速的开发。书山有路勤为径,学海无涯苦作舟。我是秋知叶i、期望每一个阅读了我的文章的开发者都能够有所成长。 一、下载JDK JDK官网 这里下载 JDK17 windows x64 installer 二、安装JDK 双击打开下载的 j…...
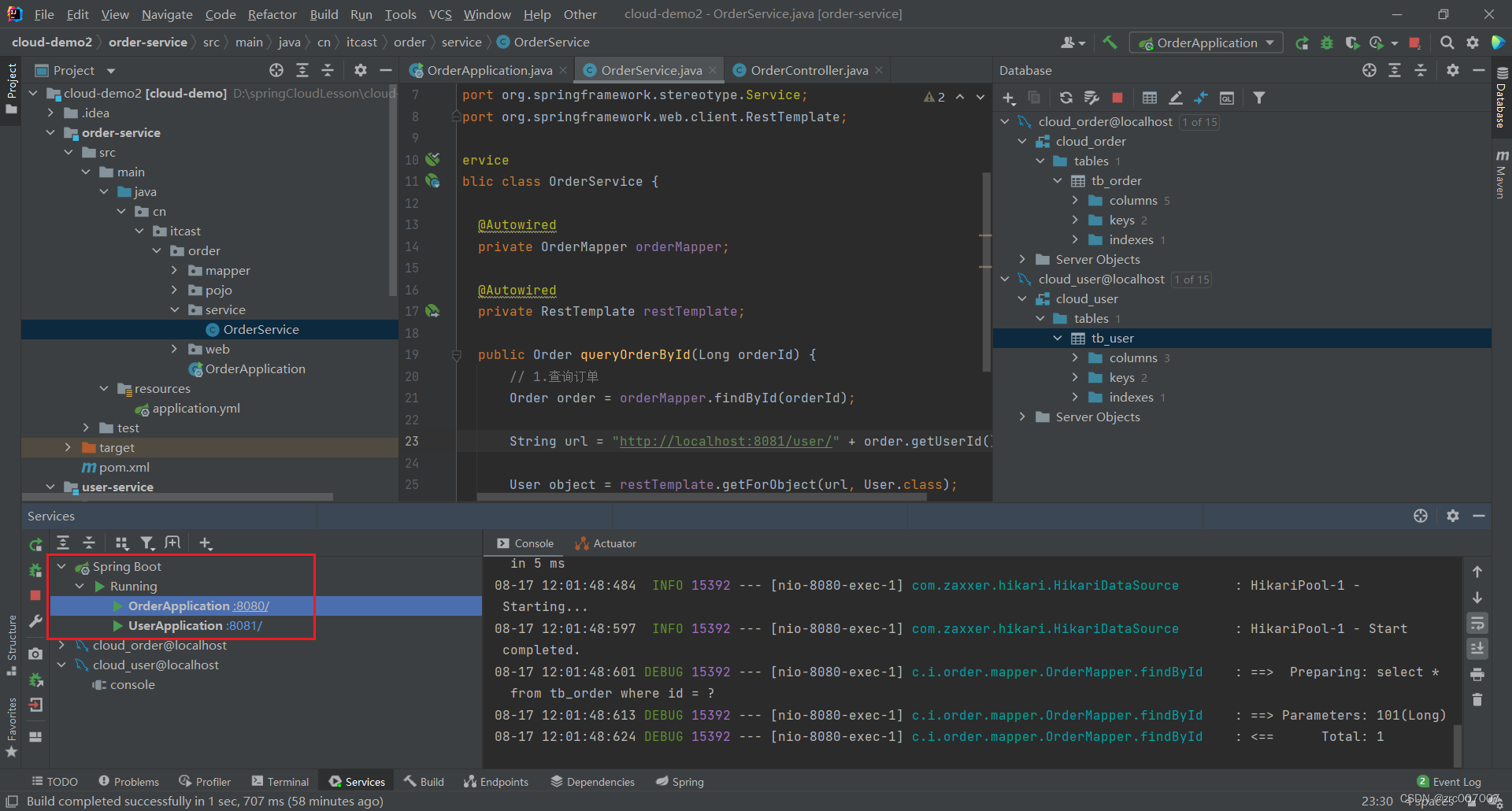
IDEA下方工具栏SideBar没有Services解决方法 IDEA配合微服务学习多端口管理打开Services栏方法
问题 微服务学习时,一次要打开多个端口,比如8080给order模块、8081给user模块……这就需要用idea管理多端口。 这时候就可以用到Services栏进行管理。 解决 首先看下方Sidebar没有Services。 打开Services 打开方式一:手动打开 在IDEA中…...

[Vue warn]: Error in render: “SyntaxError: “undefined“ is not valid JSON“
[Vue warn]: Error in render: “SyntaxError: “undefined” is not valid JSON” 这说明出现了undefined这个变量类型,比如JSON.parse()时候会出现,可以先尝试打印JSON.parse()括号中的内容是否是undefined,如果是,那问题的根源…...

ui设计师工作总结及计划范文模板
ui设计师工作总结及计划范文模板【篇一】 白驹过隙,转眼间某某年已近结尾,时间伴随着我们的脚步急驰而去,到了个人工作总结的时候,蓦然回首,才发现过去的一年不还能画上圆满的句号,内心感慨万千,…...
【Kafka】2.在SpringBoot中使用官方原生java版Kafka客户端
目 录 1. 新建一个消息生产者2. 新建一个消息消费者3. 测 试 在开始之前,需要先做点准备工作,用 IDEA 新建一个 Maven 项目,取名 kafka-study,然后删掉它的 src 目录,接着在 pom.xml 里面引入下面的依赖。这个项目的作…...
使用腾讯云轻量服务器Matomo应用模板建网站流量统计系统
腾讯云百科分享使用腾讯云轻量应用服务器Matomo应用模板搭建网站流量统计系统,Matomo 是一款开源的网站数据统计软件,可以用于跟踪、分析您的网站的流量,同时充分保障数据安全性、隐私性。该镜像基于 CentOS 7.6 64位操作系统,已预…...
clickhouse-监控配置
一、概述 监控是运维的一大利器,要想运维好clickhouse,首先就要对其进行监控,clickhouse有几种监控数据的方式,一种是系统本身监控,一种是通过exporter来监控,下面分别描述一下 二、系统自带监控 我下面会对监控做一…...
互斥量概念、用法、死锁演示及解决详解)
C++11并发与多线程笔记(5)互斥量概念、用法、死锁演示及解决详解
C11并发与多线程笔记(5)互斥量概念、用法、死锁演示及解决详解 1、互斥量(mutex)的基本概念2、互斥量的用法2.1 lock(),unlock()2.2 lock_guard类模板 3、死锁3.1 死锁演示3.2 死锁的一般解决方案:3.3 std:…...
华为云classroom赋能--Devstar使应用开发无需从零开始
华为云DevStar为开发者提供业界主流框架代码初始化能力,通过GUI、API、CLI等多种方式,将按模板生成框架代码的能力推送至用户桌面。同时基于华为云服务资源、成熟的DevOps开发工具链和面向多场景的众多开发模板,提供一站式创建代码仓、自动生…...

软件的数据回滚
原理:所谓的数据回滚,就是数据备份 增量备份: 全量备份: 最简单的事全量备份。 就是spoon工具,完成把所有的表每天定时复制一份,表名“_日期”。 所以有实时表,每日备份表。 回滚就是把之前…...

git clone使用https协议报错OpenSSL SSL_read: Connection was reset, errno 10054
在使用git 下载github上的代码时, 一般有ssh协议和https协议两种。使用ssh协议可以成功clone代码, 但使用https协议时出错: $ git clone https://github.com/openai/improved-diffusion.git Cloning into improved-diffusion... fatal: unab…...
化繁为简,使用Hibernate Validator实现参数校验
前言 在之前的悦享校园的开发中使用了SSM框架,由于当时并没有使用参数参数校验工具,方法的入参判断使用了大量的if else语句,代码十分臃肿,因此最近在重构代码时,将框架改为SpringBoot后,引入了Hibernate V…...

【Qt】多线程
线程创建 自定义线程类 #ifndef CUSTOMETHREAD_H #define CUSTOMETHREAD_H#include <QObject> #include <QThread> #include "add.h"class CustomeThread : public QThread {Q_OBJECT public:// Bind the thread kernel function.explicit CustomeThre…...
腾讯云GPU服务器GN7实例NVIDIA T4 GPU卡
腾讯云GPU服务器GN7实例搭载1颗 NVIDIA T4 GPU,8核32G配置,系统盘为100G 高性能云硬盘,自带5M公网带宽,系统镜像可选Linux和Windows,地域可选广州/上海/北京/新加坡/南京/重庆/成都/首尔/中国香港/德国/东京/曼谷/硅谷…...
3. 爬取自己CSDN博客列表(自动方式)(分页查询)(网站反爬虫策略,需要在代码中添加合适的请求头User-Agent,否则response返回空)
文章目录 步骤打开谷歌浏览器输入网址按F12进入调试界面点击网络,清除历史消息按F5刷新页面找到接口(community/home-api/v1/get-business-list)接口解读 撰写代码获取博客列表先明确返回信息格式json字段解读 Apipost测试接口编写python代码…...

利用HTTP代理实现请求路由
嘿,大家好!作为一名专业的爬虫程序员,我知道构建一个高效的分布式爬虫系统是一个相当复杂的任务。在这个过程中,实现请求的路由是非常关键的。今天,我将和大家分享一些关于如何利用HTTP代理实现请求路由的实用技巧&…...
深度学习(36)—— 图神经网络GNN(1)
深度学习(36)—— 图神经网络GNN(1) 这个系列的所有代码我都会放在git上,欢迎造访 文章目录 深度学习(36)—— 图神经网络GNN(1)1. 基础知识2.使用场景3. 图卷积神经网…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
