LeetCode Top100 Liked 题单(序号34~51)
34. Find First and Last Position of Element in Sorted Array
题意:找到非递减序列中目标的开头和结尾
我的思路
用二分法把每一个数字都找到,最后返回首尾两个数
代码 Runtime12 ms Beats 33.23% Memory14 MB Beats 5.16%
class Solution {
public:void bins(int l,int r,int tar,vector<int>& nums,vector<int>& ans){while(l<=r){int mid=l+(r-l)/2;if(nums[mid]>tar) r=mid-1;else if(nums[mid]<tar)l=mid+1;else{ans.push_back(mid);bins(l,mid-1,tar,nums,ans);bins(mid+1,r,tar,nums,ans);return ;}}}vector<int> searchRange(vector<int>& nums, int target) {int n=nums.size();vector<int> ans;bins(0,n-1,target,nums,ans);if (ans.empty())return {-1,-1};else sort(ans.begin(),ans.end());return {ans[0],ans[ans.size()-1]};}
};标答
可以直接找到序列的头部数字,和数字加一的序列的头部数字
代码 Runtime 3 ms Beats 96.59% Memory13.7 MB Beats 11.32%
class Solution {
public:pair<int,int> bins(vector<int>& nums,int tar,int l,int r){int ans=-1;while(l<=r){int mid=(l+r)/2;if(tar>nums[mid]) l=mid+1;else if(tar<nums[mid]) r=mid-1;else{//如果等于的话ans=mid;r=mid-1;}}if(ans==-1)return {l,0};return {ans,1};}vector<int> searchRange(vector<int>& nums, int target) {int n=(int)nums.size()-1;pair<int,int> st; pair<int,int> en;st =bins(nums,target,0,n);en =bins(nums,target+1,0,n);if(!st.second) return {-1,-1};return {st.first,en.first-1};}
};35. Search Insert Position
题意:给定一个有序数组和一个元素,找到给序号,没找到返回他应该插在哪里
我的思路
二分查找,我记得二分查找应该是有upper_bound和lower_bound直接用的
注意:lower_bound函数是返回指针,用于在指定区域内查找不小于目标值的第一个元素,也就是说[1,2,3,5]数组中,target为4的情况下返回的是序号为3;[1,2,3,4]数组中,target为4的情况下返回的是序号为3
upper_bound为大于目标元素的第一个数/位置,[1,2,3,5]数组中,target为4的情况下返回的是序号为3;[1,2,3,4]数组中,target为4的情况下返回的是序号为4
代码 3ms Beats 88.42% 9.63mb Beats 47.66%
class Solution {
public:int searchInsert(vector<int>& nums, int target) {return lower_bound(nums.begin(), nums.end(), target) - nums.begin();}
};39. Combination Sum
题意:给定一个不同整数数组和一个目标,返回一个单独的集合,使得集合内部和等于target;同一个数字可以用多次;
我的思路
好像是动态规划做的?和背包问题差不多,但是我忘记了orz
标答 动态规划
首先创建一个dp的vector,每个dp的内容是答案的格式,也就是vector<vector<int>>,dp表示的是从第一个数开始到target的每个数为target时的答案
状态转移方程为 dp[j]=dp[j-i]+i (这里的+时集合加入的意思)
代码 Runtime 18 ms Beats 34.7% Memory14.3 MB Beats 40.40%
class Solution {
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {vector <vector <vector<int>>> dp(target+1);//首先要开辟空间,不然会runtime errordp[0]={{}}; //初始化for(int &i:candidates){//对于每一个在候选名单里的for(int j=i;j<=target;j++){//对于每个在数组里的ifor(auto v:dp[j-i]){//v是每一个答案中的集合v.push_back(i);dp[j].push_back(v);//要把更新的集合放回dp[j]中}}}return dp[target];}
};标答 递归
递归的方法好像速度更快,首先将数组排序,之后递归,递归的引入参数为num;next是nums的索引,也就是遍历了nums的每一个数字;psol是每一个集合,表示拿或者不拿的可能性;target是目标;result是最后的答案
注意:在一开始要排序,这么做是为了剪枝操作
因为 if(target<0)return; 这一操作同样可以退出递归,但是如果target-candidates[next]<0 的时候推出递归,那么可以剪枝,大大提升速度;如果要达成这target-candidates[next]<0退出的操作,那么就必须要nums排序,这一才能加快速度
注意:psol传入时要引用,不然会拖慢时间
代码 Runtime2 ms Beats 91.39% Memory10.7 MB Beats 84.74%
class Solution {
public:void search(vector<int>& candidates, int next, int target, vector<int>& pol, vector<vector<int>> &result){if(target==0){//说明结束了result.push_back(pol);return;}if(next==candidates.size()||target-candidates[next]<0) return;pol.push_back(candidates[next]);//这是拿了,注意拿了还可以接着拿search(candidates,next,target-candidates[next],pol,result);pol.pop_back();search(candidates,next+1,target,pol,result);//这是没拿,没拿就走了}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {sort(candidates.begin(),candidates.end());vector<int> pol;vector<vector<int>> result;//初始化search(candidates,0,target,pol,result);return result;}
};41. First Missing Positive
题意:给出未排序的nums,返回未在这些数字中的正整数
我的思路
好像博弈论中有这个算法,还涉及位运算?但是忘记了【好吧,答案中没有位运算】
num的长度只有1e5,所以只能写一个O n的算法了
代码 Runtime 38 ms Beats 98.63% Memory41.3 MB Beats 34.99%
class Solution {
public:int firstMissingPositive(vector<int>& nums) {bool vis[100005]={0};int n=nums.size();for(int i=0;i<n;i++){if(nums[i]>100000||nums[i]<=0)continue;vis[nums[i]]=1;}for(int i=1;i<=100001;i++){if(vis[i]==0)return i;}return 0;}
};另一道题 涉及位运算
给定一个包含 0, 1, 2, ..., n 中 n 个数的序列,找出 0 .. n 中没有出现在序列中的那个数。
输入: [3,0,1]
输出: 2
输入: [9,6,4,2,3,5,7,0,1]
输出: 8
运用位运算来完成,思路为temp ^ nums[ i ] ^ (i + 1),这里的temp值从0开始,因为nums 的值是从0开始,而(i + 1)则是为了取到自然数1,2,3,4,5...等。运算规则如下:假如目标数组nums 值 为 0,1,2,4 自然数对应为1,2,3,4
0 ^ 1 ^ 0 = 1
1 ^ 2 ^ 1 = 2
2 ^ 3 ^ 2 = 3
3 ^ 4 ^ 4 = 3
返回值为3 缺失的数字即为3
class Solution {
public:int firstMissingPositive(vector<int>& nums) {int temp = 0;for(int i = 0;i < nums.size();i++){temp = temp ^ (i + 1) ^ (nums[i]);}return temp;}
};
42. Trapping Rain Water
题意:给一组正整数数组,表示宽度为1的砖块的高度,问能存多少水
我的思路
费案1
单调栈,同时要记录下每个砖块的距离,所以栈里面存的是序号,一层一层的扫描?首先是y等于1之间的砖块,之后是y=2之间的砖块
假设是9 6 2 0 3 0 2 5 ,就是先9和6和3和0放入栈中;【如果一开始是0,就不放进去了】
height【i】=3来了把0弹出来,那么就直接弹出,之后栈顶是2,在计算0的那一个步骤,ans加上min(目前栈顶=2,height【i】=3)的数值,ans+=2;
目前栈顶是2,发现小于等于height【i】=3,那么就直接弹出,之后栈顶是6,在计算2的那一个步骤,ans+=id的差=2 * (height【i】=3 - 上一个弹出的数=2)的数值,ans+=2;当前栈为9 6 3
height【i】=0,不弹出;
height【i】=2,把0弹出来,直接弹出,之后栈顶是3,在计算0的那一个步骤,ans+=id的差=1 * (height【i】=2 - 上一个弹出的数=0),ans+=2,目前栈为9 6 3 2
height【i】=5,目前栈顶是2,发现小于等于height【i】=5,直接弹出,之后栈顶是3,在计算0的那一个步骤所以ans=ans+(i=7 - top的序号=6-1 )*(height【i】 - 上一个弹出的值=2),ans+=0,当前栈为9 6 3 ans不对
费案2
用减法,先减去砖块占用水的体积
例如1 0 2 0 3 0 2 5 ,从右向左,mx=5,扫完一遍了,假设-1的位置有无限高的墙,
所以ans=【7-(-1)-1】*5-所有砖块的体积,不对
标答 双指针法 竖着加的
和上面的减法的思路差不多,但他是一个个竖着加起来
lmax代表最左边的墙,rmax代表最右边的墙前两个if表示的是目前的lmax和rmax都不是最高的,应该要更新;第三个条件如果rmax大于lmax,ans加上lmax-h[lpos];第四个条件如果lmax大于rmax,ans加上rmax-h[rpos];为什么那么做?因为如果整个盆子左边高于右边,那么右侧的水肯定能装住,如果整个盆子右边高于左边,那么左侧的水肯定能装住。
代码 Runtime6 ms Beats 97.75% Memory19.8 MB Beats 53.37%
注意 lpos<=rpos的等号
class Solution {
public:int trap(vector<int>& h) {int n=h.size()-1;int lmax=h[0],rmax=h[n];int lpos=1,rpos=n-1,ans=0;while(lpos<=rpos){ //等号if(rmax<=h[rpos]){rmax=h[rpos];rpos--;}else if(lmax<=h[lpos]){lmax=h[lpos];lpos++;}else if(rmax>=lmax){ans+=(lmax-h[lpos]);lpos++;}else{ans+=(rmax-h[rpos]);rpos--;}}return ans;}
};标答 前缀和 竖着加的
dp[i]表示从左到右,以左边的边作为最高的边,每个横坐标 i 能装多少水;之后从右到左,以右边的边作为最高的边,res在每个横坐标 i 上加上min ( 当前的最高 - dp[i] )
代码 Runtime 12 ms Beats 78.67% Memory19.8 MB Beats 53.37%
class Solution {
public:int trap(vector<int>& h) {int n=h.size(),dp[20004]={0};int curmax=-1,ans=0;for(int i=0;i<n;i++){curmax=max(curmax,h[i]);dp[i]=curmax-h[i];}curmax=-1;for(int i=n-1;i>=0;i--){curmax=max(curmax,h[i]);ans+=min(dp[i],curmax-h[i]);}return ans;}
};标答 单调栈 横着加的
和费案1的思路相仿。栈中的数字越来越小,如果来了一个大的数,把这个数弹出,设cur是这个弹出的数,diff的序号的差,ans+=(min(当前栈顶的数,height[i] ) - 上一个弹出的数)*序号的差
为什么想费案1的时候没有想出来呢?
height【i】=5,目前栈顶是2,发现小于等于height【i】=5,直接弹出,之后栈顶是3,在计算0的那一个步骤所以ans=ans+(i=7 - top的序号=6-1 )*(height【i】 - 上一个弹出的值=2),ans+=0,当前栈为9 6 3
因为从最上面的图中可以看出,之前的步骤都是ans+=(min(当前栈顶的数,height[i] ) - 上一个弹出的数),但是当h[i]=5时,ans+=(当前栈顶的数 上一个弹出的数),没有办法把公式统一起来,所以没做出来,明明只要加上取最小就可以了
为什么是取最小呢?
原理和标答1的原理是差不多的,因为答案是和两侧最小的那一条有关
补充:
1. 费案1中的栈根本不需要pair结构,因为有序号有数组就知道了数值了
2. if(st.empty())break;这条语句是指左边没有边可以作为盘子的左边了,装不下水了,所以break了
代码 Runtime 12 ms Beats 78.67% Memory19.8 MB Beats 53.37%
class Solution {
public:int trap(vector<int>& h) {stack<int> st;int n=h.size(),ans=0;for(int i=0;i<n;i++){while(!st.empty()&&h[st.top()]<h[i]){//弹出操作int temp=st.top();st.pop();if(st.empty())break;//注意这句话int cha=i-st.top()-1;//注意这里是-1!!!!!!!ans+=(min(h[i],h[st.top()])-h[temp])*cha;}st.push(i);}return ans;}
};45. Jump Game II
题意:有n个序号从0开始的数组,你可以从num[i],向右跳到【num[i],num[i+j]】之间
我的思路
动态规划,dp表示需要最少的次数,一开始初始化为无穷,dp[n-1]=0,最外层循环是i从n-1到0,第二层循环是j从1到num[i],找到循环中最小的dp[i+j],dp[i]=min( dp[ i + j ] + 1 ),返回答案dp[0]
但不幸的是n是1e4,nums是1e3,时间复杂度1e7
代码 Runtime128 ms Beats 39.88% Memory16.8 MB Beats 41.3%
class Solution {
public:int jump(vector<int>& nums) {int n=nums.size();int dp[10004];for(int i=0;i<n;i++)dp[i]=9999;dp[n-1]=0;for(int i=n-2;i>=0;i--){int minn=9999;for(int j=1;j<=nums[i] && i+j<n;j++) minn=min(minn,dp[i+j]);dp[i]=minn+1;}return dp[0];}
};要优化的话肯定是优化第二个循环,快速找到某个范围内的最小值,想到树状数组,去看了看树状数组的板子,找到的树状数组代码维护的是【1,i】范围的最小值,网上说只有树状数组套树状数组或者线段树才可以达到动态维护区间最小值
但是线段树要从1开始建立,同时修改的时候不是单纯的增减,而是直接替换,所以线段树也不适合
标答 贪心
为什么可以用贪心算法呢?
乍一看想到动态规划去了,才发现忽略了最大步长的信息(没有的话就是DP了),因此不需要考虑跳多了的情况,而且题面能够保证绝对能到达,所以不用担心0步长的情形(跳不出去啦!)。
因此本题可以直接使用贪心算法:向后遍历,找出能够跳的最远的选择。
贪心最麻烦的地方就是全局最优解的证明,我这里给出一个简单的思路:从同一个起点出发,如果当前选择不是贪心选择的,那么下一个选择必然比贪心方案跳的更近。完成一次跳跃后有两种情形:贪心方案的第二次选择的位置是否存在于当前方案的第二次选择中。存在,则最多选择这个方案,此时当前方案会比贪心方案段(第二次选择一样,但是第一次选择短了);不存在,那么肯定是会短的(两次选择都短)。
参考链接:https://blog.csdn.net/cary_leo/article/details/115451900
简单来说就是比谁跳的远
代码 Runtime 8 ms Beats 95.22% Memory16.6 MB Beats 64.1%
class Solution {
public:int jump(vector<int>& nums) {int n=nums.size(),ans=0;for(int i=1;i<n;i++){//要么选择在这一格跳走,要么就留在这里nums[i]=max(nums[i-1],nums[i]+i);//nums代表在i位置可以到达的最远的位置}int st=0;while(st<n-1){ans++; st=nums[st];}return ans;}
};
46. Permutations
题意:有一个数组,里面的数字各不相同,返回所有排列
我的思路
用dfs做,没写出来;我好像还记得C++库中有个直接全排列的调用
标答 dfs 回溯法
照着我写坏的和表达对照一下,我用了两次dfs,一次是没取走数字,一次是取走了数字;不需要没取走数字的那一组,因为他会因为个数不够而不能加入最终答案的vector,所以只要取走的那一次dfs就可以了
代码 Runtime 6 ms Beats 18.86% Memory8.2 MB Beats 11.7%
class Solution {
public:void dfs(vector<int>& nums,vector<int>& pol,vector<vector<int>>& ans,vector<int> vis){if(pol.size()==nums.size()){ans.push_back(pol);return;}for(int i=0;i<nums.size();i++){if(vis[i]) continue;vis[i]=1;pol.push_back(nums[i]);dfs(nums,pol,ans,vis);pol.pop_back();vis[i]=0;}}vector<vector<int>> permute(vector<int>& nums) {vector<int> pol; vector<vector<int>> ans; vector<int> vis((int)nums.size(),0);dfs(nums,pol,ans,vis);return ans;}
};标答 dfs 交换
确实,不断交换就可以排序完成了,还不会有多余的没到个数的pol(和上一个做法不同)
代码 Runtime 5 ms Beats 29.21% Memory 7.5 MB Beats 81.96%
class Solution {
public:vector<vector<int>> result;void permutation(vector<int> &nums,int i,int n){if(i==n){result.push_back(nums);return ;}for(int j=i;j<=n;j++){swap( nums[i],nums[j]);permutation(nums,i+1,n);//注意这里是i+1swap( nums[i],nums[j]);}}vector<vector<int>> permute(vector<int>& nums) {permutation(nums,0,nums.size()-1);return result;}
};48. Rotate Image
题意:将整个矩阵顺时针旋转90度,注意不要新开一个矩阵
我的思路
按照这个顺序,一个圈层只要3组交换就可以了,实际操作的时候注意 i 和 j 的范围!!!!!
例子1:初始
1 2 3
4 5 6
7 8 9
第一次
7 2 3
8 5 6
9 4 1
第二次
7 2 1
8 5 4
9 6 3
第三次
7 4 1
8 5 2
9 6 3
例子2:初始
4 8
3 6
第一次
3 8
6 4
第二次
3 4
6 8
第三次
循环直接结束了
代码 Runtime 0 ms Beats 100% Memory 7.2 MB Beats 14.63%
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n=matrix.size();for(int i=0;i<n/2;i++){//圈层for(int j=i;j<n-i;j++){swap(matrix[j][i],matrix[n-1-i][j]);}for(int j=i+1;j<n-i;j++){swap(matrix[n-1-i][j],matrix[n-1-j][n-1-i]);}for(int j=i+1;j<n-1-i;j++){swap(matrix[i][j],matrix[j][n-1-i]);}}}
};标答 思维
先对角反转,之后逆向
例子1:初始
1 2 3
4 5 6
7 8 9
第一次
1 4 7
2 5 8
3 6 9
第二次
7 4 1
8 5 2
9 6 3
代码 Runtime 0 ms Beats 100% Memory7.3 MB Beats14.63%
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n = matrix.size();int m = matrix[0].size();vector<vector<int>> temp(n, vector<int>(m, 0));for(int i=0; i<n; i++){for(int j=0; j<i; j++){swap(matrix[i][j], matrix[j][i]);}}for(int i=0; i<n; i++){reverse(matrix[i].begin(), matrix[i].end());}}
};
49. Group Anagrams
题意:给一组字符串,把字母相同的字符串放在一组里
我的思路
只能想到死做,就是map映射,key是字典序排列,value是vector<string>,之后遍历map,组成答案
代码 Runtime 30 ms Beats83.8% Memory20.8 MB Beats 30.73%
class Solution {
public:vector<vector<string>> groupAnagrams(vector<string>& strs) {map<string,vector<string> > mp;int n=strs.size();for(int i=0;i<n;i++){string tmp=strs[i];sort(tmp.begin(),tmp.end());mp[tmp].push_back(strs[i]);}vector< vector<string> > ans;for(auto q:mp)ans.push_back(q.second);return ans;}
};优化
看了标答,确实是这样做的,但是sort和map和遍历可以优化,map改成unorder_map,for(auto q:mp)加上引用【这一步突然时间少一半】
代码 Runtime 15 ms Beats 99.87% Memory19.5 MB Beats 84.31%
class Solution {
public:vector<vector<string>> groupAnagrams(vector<string>& strs) {unordered_map<string,vector<string> > mp;int n=strs.size();for(int i=0;i<n;i++){string tmp=strs[i];sort(tmp.begin(),tmp.end());mp[tmp].push_back(strs[i]);}vector< vector<string> > ans;for(auto &q:mp)ans.push_back(q.second);return ans;}
};51. N-Queens
题意:皇后攻击的范围是所属的横线、竖线、斜线,在n*n的棋盘上摆放皇后,使得n个皇后不会互相攻击
我的思路
递归
代码 Runtime4 ms Beats 78.35% Memory7.8 MB Beats 36.39%
class Solution {
public:bool check(int n,int id, int j, vector<int>&pol){for(int i=0;i<pol.size();i++)if(pol[i]==j) return 0;for(int i=0;i<pol.size();i++){if(pol[i]-i ==j-id)return 0;}for(int i=0;i<pol.size();i++){if(pol[i]+i ==j+id)return 0;}return 1;}void se(int n,int id, vector<int>&pol, vector<vector<string>> & result) {if(pol.size()==n){vector<string> mp;for(int j=0;j<n;j++){//列string s (n, '.');s[pol[j]]='Q';mp.push_back(s);}result.push_back(mp);return;}for(int j=0;j<n;j++){//列if(!check(n,id,j,pol))//判断这一列上有无其他数字,判断斜线上有无其他数字;如果不可以放在这里,就跳过continue;pol.push_back(j);se(n,id+1,pol,result);pol.pop_back();}}vector<vector<string>> solveNQueens(int n) {vector<int> pol; vector<vector<string>> result;//假设返回的vector<int>表示每一行的皇后放在第n列se(n,0,pol,result);//id代表在第几行return result;}
};优化 位运算 没看懂
10394 用位运算速解 n 皇后问题 - 知乎 (zhihu.com)
class Solution {
public:vector <vector <string>> ans;void solve(int n, int row, int colMask, int leftDiagMask, int rightDiagMask, vector <string> &board) {if (row == n) {ans.push_back(board);return;}int rowState = (colMask | leftDiagMask | rightDiagMask) & ((1 << n) - 1);int safePos = rowState ^ ((1 << n) - 1);while (safePos) {int queenPos = safePos & (-safePos);safePos -= queenPos;if (!(queenPos & rowState)) {board[row][log2(queenPos)] = 'Q';solve(n, row + 1, colMask | queenPos, (leftDiagMask | queenPos) << 1, (rightDiagMask | queenPos) >> 1, board);board[row][log2(queenPos)] = '.';}}}vector<vector<string>> solveNQueens(int n) {vector <string> board(n, string (n, '.'));solve(n, 0, 0, 0, 0, board);return ans;}
};相关文章:

LeetCode Top100 Liked 题单(序号34~51)
34. Find First and Last Position of Element in Sorted Array 题意:找到非递减序列中目标的开头和结尾 我的思路 用二分法把每一个数字都找到,最后返回首尾两个数 代码 Runtime12 ms Beats 33.23% Memory14 MB Beats 5.16% class Solution {…...
视觉slam十四讲---第一弹三维空间刚体运动
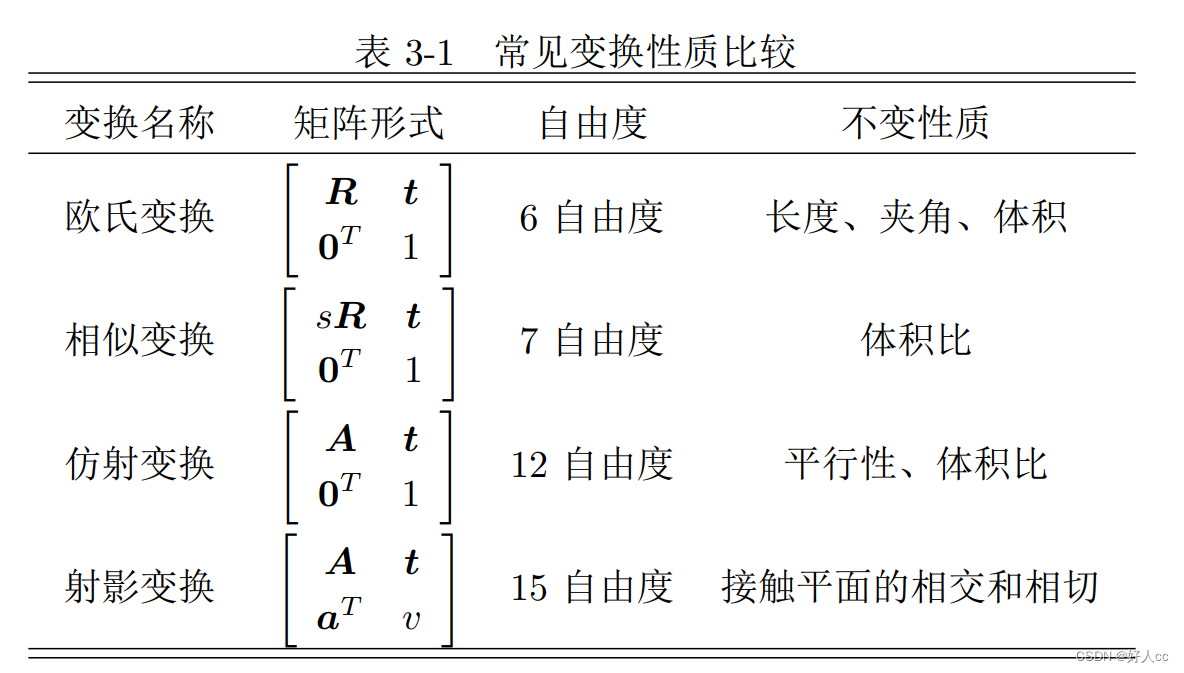
1.旋转矩阵 1.1内积 1.2外积 1.3坐标系间的欧式变换 相机运动是一个刚体运动,它保证了同一个向量在各个坐标系下的长度和夹角都不会 发生变化。这种变换称为欧氏变换。 旋转矩阵:它是一个行列式为 1 的正交矩阵。 旋转矩阵为正交阵,它的逆…...
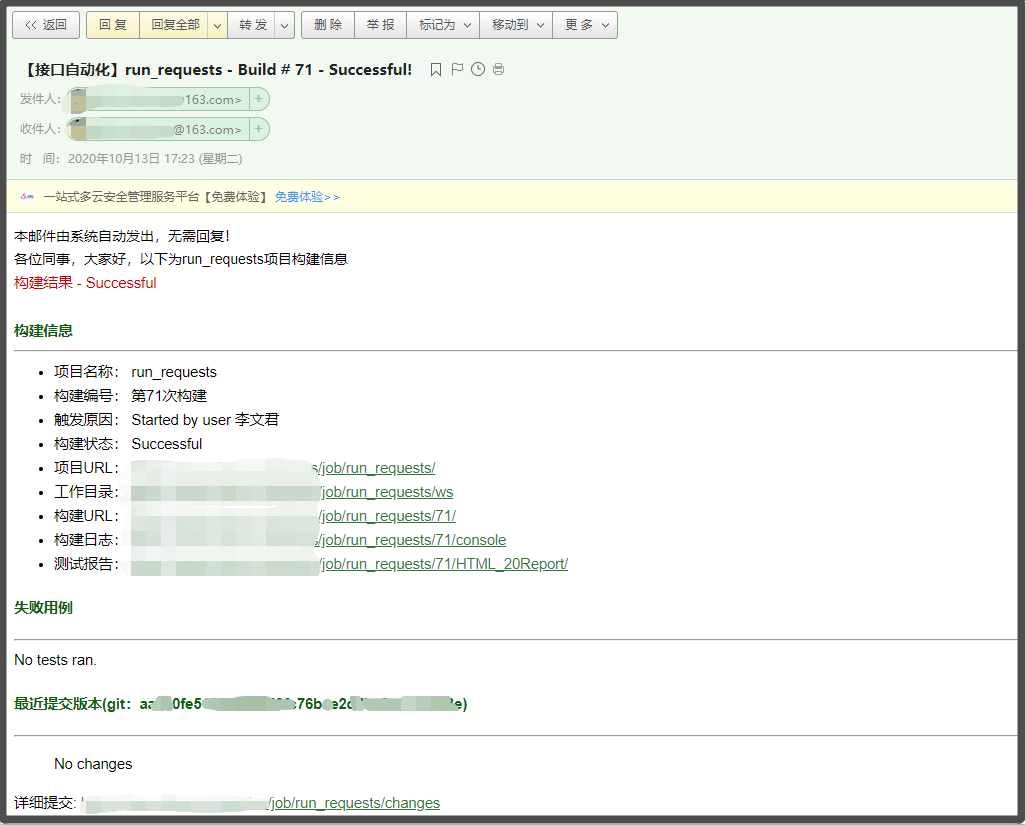
手把手教你配置Jenkins自动化邮件通知
完成基于Jenkins的持续集成部署后,自动化测试执行后,测试结果需要通知到相关人员,除了钉钉通知外我们还可以通过Email通知到对应负责人,这里记录一下测试结果通过Jenkins邮件通知的配置与部署 01、安装插件 方法1: 进…...

Arcgis连续数据的分类(求不同值域的面积)
问题描述:如果得到的一个连续的影响数值数据,但是我们想求取某一段值域的面积占比,需要进行以下操作: 1.按照数值重分类,将某段数值变成一个类别 2.栅格转矢量,再求取面积...

C++ 函数
函数是一组一起执行一个任务的语句。每个 C 程序都至少有一个函数,即主函数 main() ,所有简单的程序都可以定义其他额外的函数。 您可以把代码划分到不同的函数中。如何划分代码到不同的函数中是由您来决定的,但在逻辑上,划分通常…...

关于如何创建一个windows窗口的exe文件
如何创建一个windows窗口exe文件,具体参照这个博主: http://t.csdn.cn/pfQK5 以下是实现代码,注意用vs打开: #pragma comment( linker, "/subsystem:\"windows\" /entry:\"WinMainCRTStartup\"" …...
re学习(33)攻防世界-secret-galaxy-300(动态调试)
下载压缩包: 下载链接:https://adworld.xctf.org.cn/challenges/list 参考文章:攻防世界逆向高手题之secret-galaxy-300_沐一 林的博客-CSDN博客 发现这只是三个同一类型文件的三个不同版本而已,一个windows32位exe࿰…...
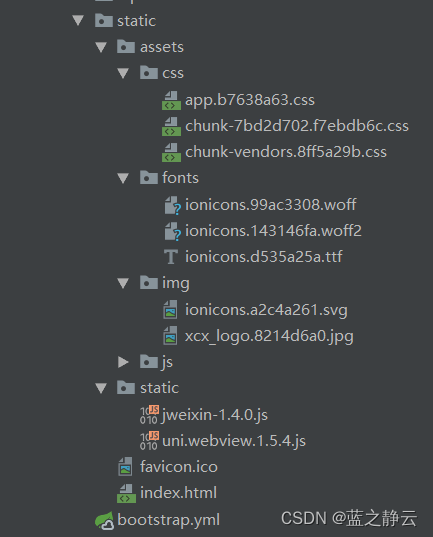
springboot工程集成前端编译包,用于uni-app webView工程,解决其需独立部署带来的麻烦,场景如页面->画布->图片->pdf
前端工程 访问方式 http://127.0.0.1:8080/context/frontEnd/index放行 public class SecurityConfig extends WebSecurityConfigurerAdapter { "/frontEnd/**",SysFrontEndController import lombok.extern.slf4j.Slf4j; import nl.basjes.shaded.org.springfram…...
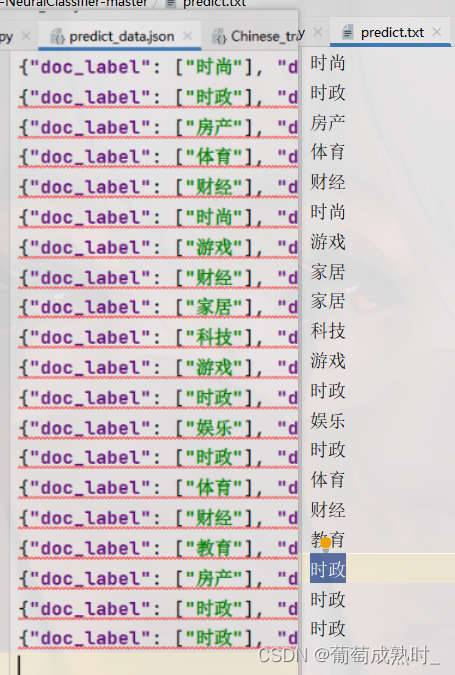
NeuralNLP-NeuralClassifier的使用记录(二),训练预测自己的【中文文本多分类】
NeuralNLP-NeuralClassifier的使用记录,训练预测自己的【中文文本多分类】 数据准备: 与英文的训练预测一致,都使用相同的数据格式,将数据通过代码处理为JSON格式,以下是我使用的一种,不同的原数据情况…...

express学习笔记8 - 文件上传 下载以及预览
一、上传 1、 安装multer (任意选其中一种) yarn add multer --S npm install multer --S 2、新建配置文件(utils/multerConfig) const multer require(multer); const mkdirp require(mkdirp); // const sd require(silly-datetime); const path require(path);con…...
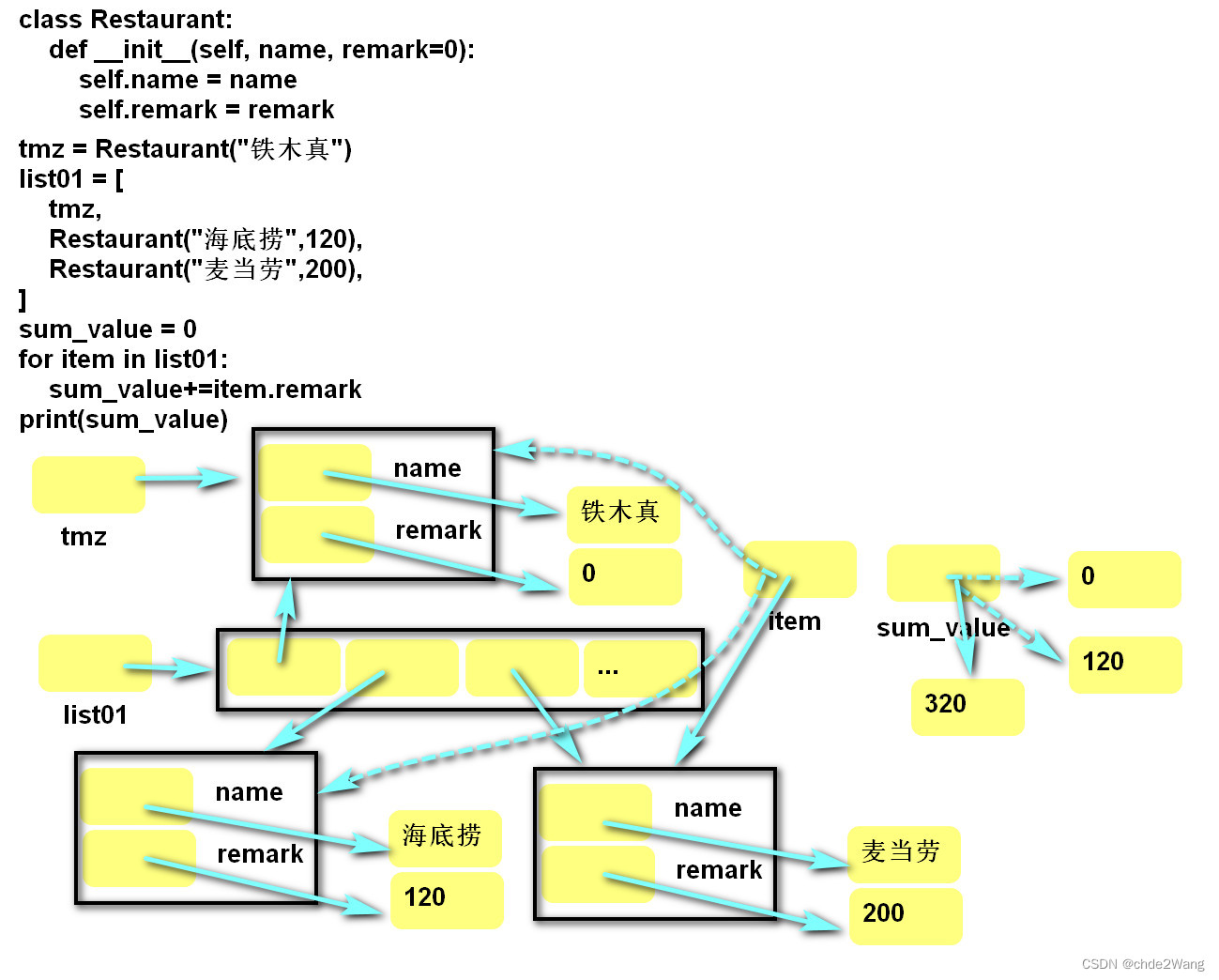
Python系统学习1-9-类(一)
一、类之初印象 1、类就是空表格,将变量(列名)和函数(行为)结合起来 2、创建对象,表达具体行 3、创建类就是创建数据的模板 --操作数据时有提示 --还能再组合数据的行为 --结构更加清晰 4、类的内存分配…...
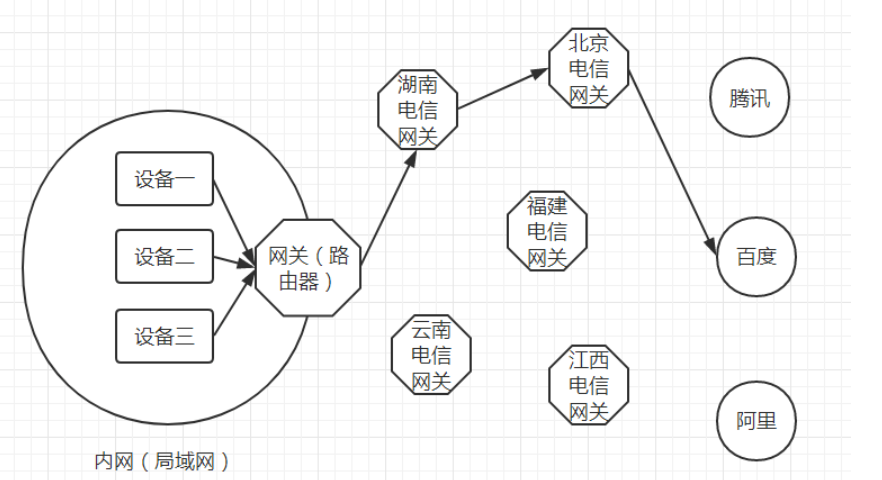
什么是公网、私网、内网、外网?
中午好,我的网工朋友。 最近经常有很多小白朋友在问,公网、私网、内网、外网,这些的概念是啥样的,又该怎么去界定。 关于IP地址,确实没有太明确的区分,其实也不必太过咬文嚼字。 内网、外网就是一个参考…...
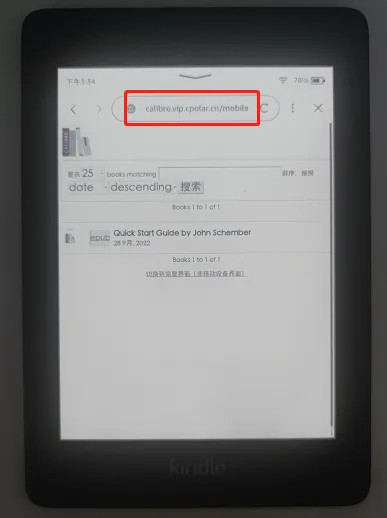
一篇文章教会你搭建私人kindle图书馆,并内网穿透实现公网访问
搭建私人kindle图书馆,并内网穿透实现公网访问 在电子书风靡的时期,大部分人都购买了一本电子书,虽然这本电子书更多的时候是被搁置在储物架上吃灰,或者成为盖泡面的神器,但当亚马逊发布消息将放弃电子书在中国的服务…...
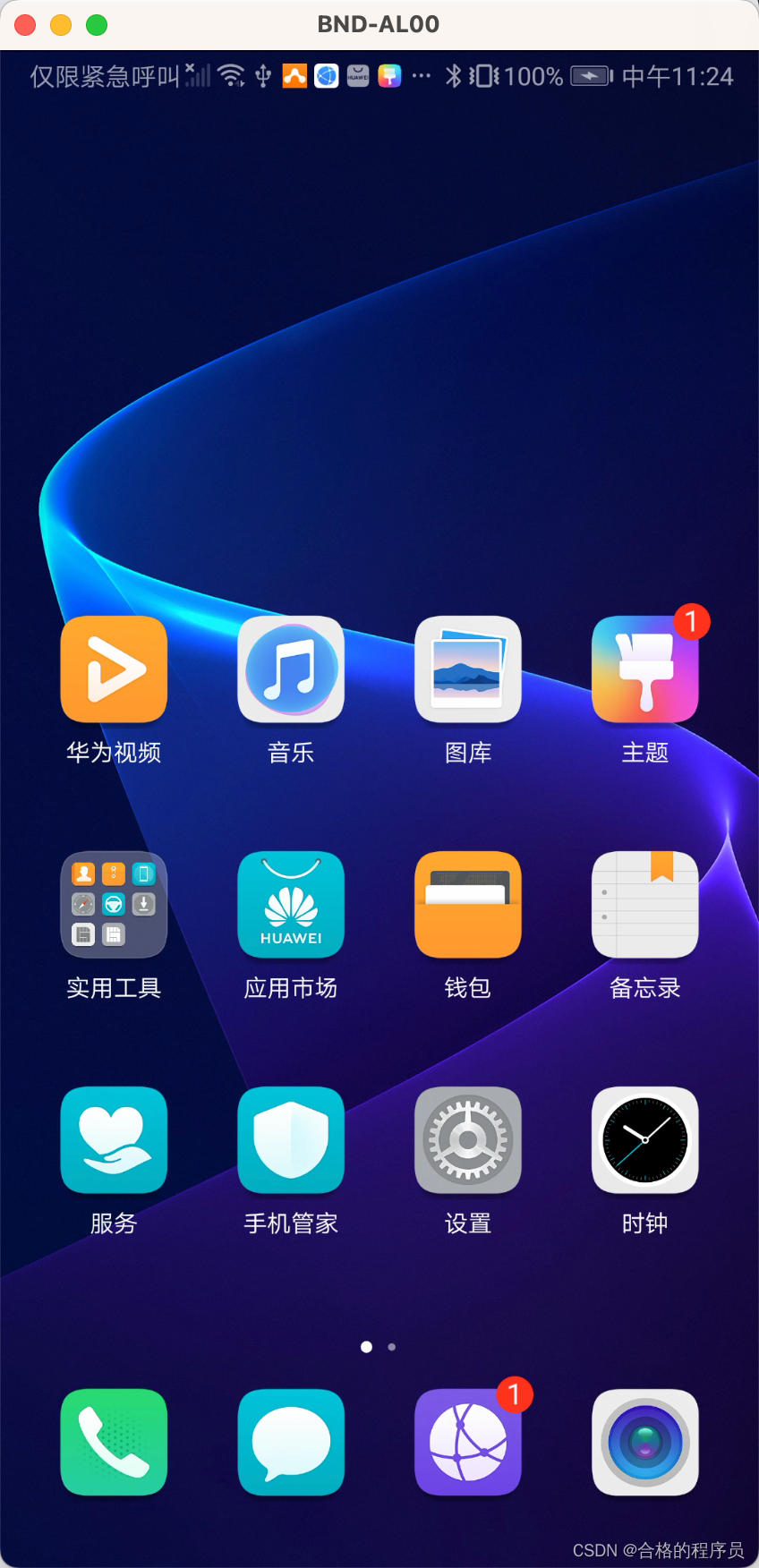
好用的安卓手机投屏到mac分享
工具推荐:scrcpy github地址:https://github.com/Genymobile/scrcpy/tree/master mac使用方式 安装环境,打开terminal,执行以下命令,没有brew的先安装brew brew install scrcpy brew install android-platform-too…...
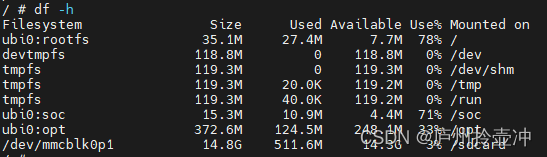
df -h
df -h 命令用于查看磁盘占用的空间 Filesystem:表示该文件系统位于哪个分区,因此该列显示的是设备名称; Used:表示用掉的磁盘空间大小; Available:表示剩余的磁盘空间大小; Use%:磁盘…...
彻底卸载Android Studio
永恒的爱是永远恪守最初的诺言。 在安装Android Studio会有很多问题导致无法正常运行,多次下载AS多次错误后了解到,删除以下四个文件才能彻底卸载Android Studio。 第一个文件:.gradle 路径:C:\Users\yao(这里yao是本…...

QT 5.12配置OpenCV3.4.10
主要过程:使用cmake编译源码,生成Mingw64位 下的OpenCV库 三篇博客解决问题: 1.Windows下安装Qt并使用cmake配置opencv3.4.10(含错误记录及解决办法)_d:\qt\qt5.14.2\5.14.2\mingw73_64\include\qtcore\qg_会飞的DA象的博客-CSDN博客 2.【…...

Qt应用开发(基础篇)——选项卡窗口 QTabWidget
一、前言 QTabWidget类继承于QWidget,是一个拥有选项卡的窗口部件。 QTabWidget类有一个选项卡栏QTabBar和一个页面区域,用来显示和选项卡相关联的界面。用户通过点击选项卡或者自定义快捷方式(ALTKey)切换页面。 二、QTabWidget类 1、count 该属…...

Socks5代理在多线程爬虫中的应用
在进行爬虫开发过程中,我们常常需要处理大量的数据,并执行多任务并发操作。然而,频繁的请求可能会引起目标网站的反爬机制,导致IP封禁或限制访问。为了规避这些限制,我们可以借助Socks5代理的强大功能,通过…...
初探)
机器学习笔记:主动学习(Active Learning)初探
1 基本介绍 监督学习问题中,存在标记成本昂贵且难以大量获取的问题。 针对一些特定任务,只有行业专家才能为样本做上准确标记。在此问题背景下,主动学习(Active Learning, AL)尝试通过选择性地标记较少数据而训练出表…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
