机器学习---对数几率回归
1. 逻辑回归
逻辑回归(Logistic Regression)的模型是一个非线性模型,
sigmoid函数,又称逻辑回归函数。但是它本质上又是一个线性回归模型,因为除去sigmoid映射函
数关系,其他的步骤,算法都是线性回归的。
可以说,逻辑回归,都是以线性回归为理论支持的。
只不过,线性模型,无法做到sigmoid的非线性形式,sigmoid可以轻松处理0/1分类问题。
首先,找一个合适的预测函数,一般表示为h函数,该函数就是需要找的分类函数,它用来预
测输入数据的判断结果。然后,构造一个Cost函数(损失函数),该函数表示预测的输出(h)与
训练数据类别(y)之间的偏差,可以是二者之间的差(h—y)或者是其他的形式。综合考虑所有
训练数据的“损失”,将Cost求和或者求平均,记为J(θ)函数,表示所有训练数据预测值与实际类
别的偏差。显然,J(θ)函数的值越小表示预测函数越准确(即h函数越准确),所以这一步需要
做的是找到J(θ)函数的最小值。找函数的最小值有不同的方法,Logistic Regression实现时有的
是梯度下降法(Gradient Descent )。
2. 二分类问题
二分类问题是指预测的y值只有两个取值(0或1),二分类问题可以扩展到多分类问题。例如:我
们要做一个垃圾邮件过滤系统,x是邮件的特征,预测的y值就是邮件的类别,是垃圾邮件还是正常
邮件。对于类别我们通常称为正类(positive class)和负类(negative class),垃圾邮件的例子
中,正类就是正常邮件,负类就是垃圾邮件。
应用举例:是否垃圾邮件分类?是否肿瘤、癌症诊断?是否金融欺诈?
3. logistic函数
如果忽略二分类问题中y的取值是一个离散的取值(0或1),我们继续使用线性回归来预测y的取
值。这样做会导致y的取值并不为0或1。逻辑回归使用一个函数来归一化y值,使y的取值在区间
(0,1)内,这个函数称为Logistic函数(logistic function),也称为Sigmoid函数(sigmoid
function)。函数公式如下:

Logistic函数当z趋近于无穷大时,g(z)趋近于1;当z趋近于无穷小时,g(z)趋近于0。Logistic
函数的图形如下:
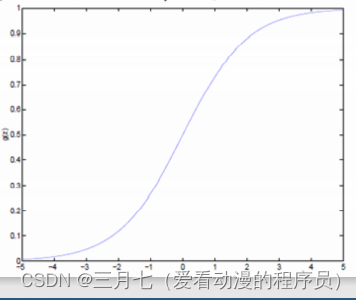
线性回归模型帮助我们用最简单的线性方程实现了对数据的拟合,然而,这只能完成回归任务,无
法完成分类任务,那么 logistics regression 就是在线性回归的基础上添砖加瓦,构建出了一种分类
模型。如果在线性模型![]() 的基础上做分类,比如二分类任务,即:y取值{0,1},
的基础上做分类,比如二分类任务,即:y取值{0,1},
最直观的,可以将线性模型的输出值再套上一个函数y = g(z),最简单的就是“单位阶跃函数”
(unit—step function),如下图中红色线段所示。
 也就是把
也就是把![]() 看作为一个分割线,大于 z 的判定为类别0,小于 z 的判定为类别1。
看作为一个分割线,大于 z 的判定为类别0,小于 z 的判定为类别1。
但是,这样的分段函数数学性质不太好,它既不连续也不可微。通常在做优化任务时,目标函数最
好是连续可微的。这里就用到了对数几率函数(形状如图中黑色曲线所示)。
它是一种"Sigmoid”函数,Sigmoid函数这个名词是表示形式S形的函数,对数几率函数就是其中最
重要的代表。这个函数相比前面的分段函数,具有非常好的数学性质,其主要优势如下:使用该函
数做分类问题时,不仅可以预测出类别,还能够得到近似概率预测。这点对很多需要利用概率辅助
决策的任务很有用。对数几率函数是任意阶可导函数,它有着很好的数学性质,很多数值优化算法
都可以直接用于求取最优解。
总的来说,模型的完全形式如下: ,LR模型就是在拟合
,LR模型就是在拟合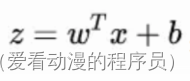
这条直线,使得这条直线尽可能地将原始数据中的两个类别正确的划分开。
对于线性边界的情况,边界形式如下:

构造预测函数为:
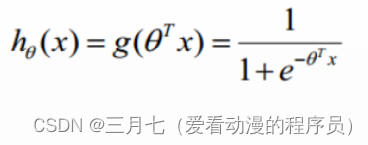
h(x)的值有特殊的含义,它表示结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分
别为:
正例(y=1) ![]()
负例(y=0) ![]()
4. 损失函数
对于任何机器学习问题,都需要先明确损失函数,LR模型也不例外,在遇到回归问题时,通常我
们会直接想到如下的损失函数形式(平均误差平方损失MSE):

但在LR模型要解决的二分类问题中,损失函数的形式是这样的:

这个损失函数通常称作为对数损失(logloss),这里的对数底为自然对数e,其中真实值 y 是有 0/1 两
种情况,而推测值由于借助对数几率函数,其输出是介于0~1之间连续概率值。仔细查看,不难发
现,当真实值y=0时,第一项为0,当真实值y=1时,第二项为0,所以,这个损失函数其实在每次
计算时永远都只有一项在发挥作用,那这就可以转换为分段函数,分段的形式如下:

5. 优化求解
现在我们已经确定了模型的损失函数,那么接下来就是根据这个损失函数,不断优化模型参数从而
获得拟合数据的最佳模型。
重新看一下损失函数,其本质上是 L 关于模型中线性方程部分的两个参数 w 和 b 的函数:

其中,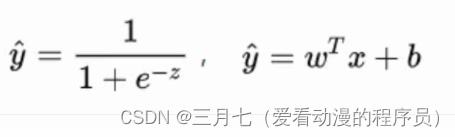
现在的学习任务转化为数学优化的形式即为:
由于损失函数连续可微,我们可以借助梯度下降法进行优化求解,对于两个核心参数的更新方式如
下:


求得:

进而求得:

转换为矩阵的计算方式为:

至此, Logistic Regression模型的优化过程介绍完毕。
6. 梯度下降算法
梯度下降法求J(θ)的最小值,θ的更新过程:


要使得最大化,则运用梯度上升法,求出最高点:
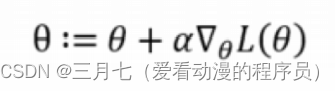
# 梯度上升,主要是采用了最大似然的推导
def gradAscent(dataMatIn,classLabels):dataMatrix = mat(dataMatIn)labelMat = mat(classLabels).transpose()m,n = shape(dataMatrix) # n=3alpha=0.001 # 学习率maxCycles=500 # 循环轮数theta = ones((n,1))for k in range(maxCycles):h=sigmoid(dataMatrix * theta)error = (labelMat - h)theta = theta + alpha * dataMatrix.transpose()*errorreturn theta
相关文章:
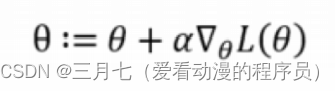
机器学习---对数几率回归
1. 逻辑回归 逻辑回归(Logistic Regression)的模型是一个非线性模型, sigmoid函数,又称逻辑回归函数。但是它本质上又是一个线性回归模型,因为除去sigmoid映射函 数关系,其他的步骤,算法都是…...
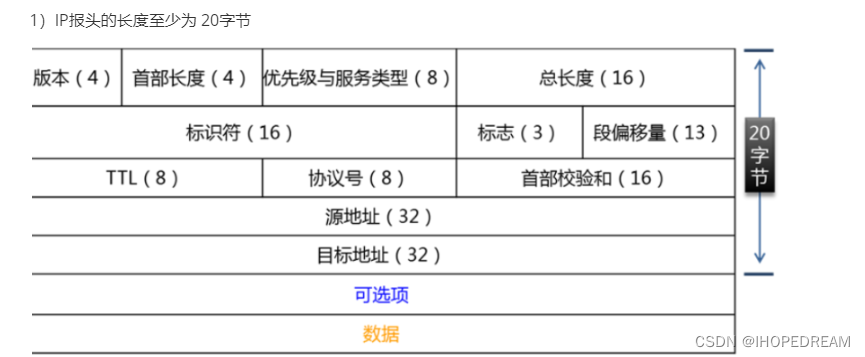
网络通信原理IP头部格式(第四十二课)
字段作用解析:1)版本: 指的IP地址的版本 (IPv4 或 IPV6)2)首部长度: 次数据包的首部长度一共是多少,没有加可选项3)优先级与服务类型:表示****数据包是否需要优选传递4)总长度: 表示的是整个数据包的大小,也就****是首部+数据5)标识符、标志、段偏移量:的作用将拆开的…...
)
Flink多流处理之join(关联)
Flink的API中只提供了join的算子,并没有left join或者right join,这里我们就介绍一下join算子的使用,其实join算子底层调用的就是coGroup,具体原理这里就不过多介绍了,如果感兴趣可以看我前面发布的文章Flink多流操作之coGroup. 数据源➜ ~ nc -lk 1111 101,A 102,B 103,C 10…...
LeetCode Top100 Liked 题单(序号34~51)
34. Find First and Last Position of Element in Sorted Array 题意:找到非递减序列中目标的开头和结尾 我的思路 用二分法把每一个数字都找到,最后返回首尾两个数 代码 Runtime12 ms Beats 33.23% Memory14 MB Beats 5.16% class Solution {…...
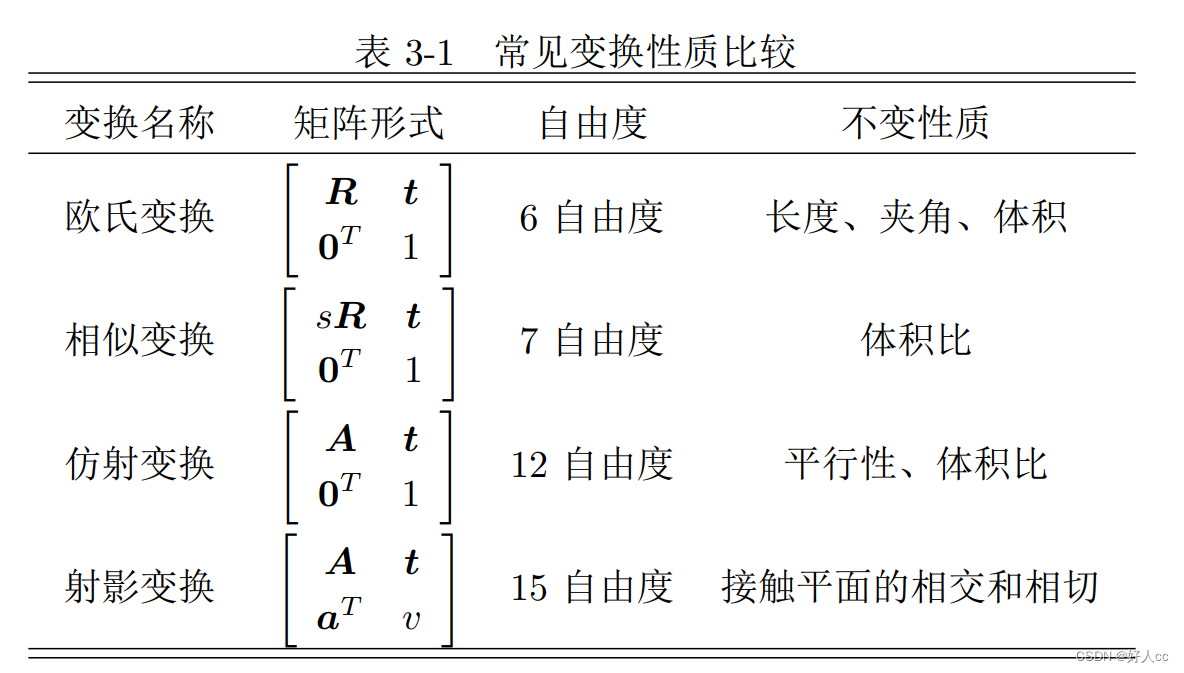
视觉slam十四讲---第一弹三维空间刚体运动
1.旋转矩阵 1.1内积 1.2外积 1.3坐标系间的欧式变换 相机运动是一个刚体运动,它保证了同一个向量在各个坐标系下的长度和夹角都不会 发生变化。这种变换称为欧氏变换。 旋转矩阵:它是一个行列式为 1 的正交矩阵。 旋转矩阵为正交阵,它的逆…...
手把手教你配置Jenkins自动化邮件通知
完成基于Jenkins的持续集成部署后,自动化测试执行后,测试结果需要通知到相关人员,除了钉钉通知外我们还可以通过Email通知到对应负责人,这里记录一下测试结果通过Jenkins邮件通知的配置与部署 01、安装插件 方法1: 进…...

Arcgis连续数据的分类(求不同值域的面积)
问题描述:如果得到的一个连续的影响数值数据,但是我们想求取某一段值域的面积占比,需要进行以下操作: 1.按照数值重分类,将某段数值变成一个类别 2.栅格转矢量,再求取面积...

C++ 函数
函数是一组一起执行一个任务的语句。每个 C 程序都至少有一个函数,即主函数 main() ,所有简单的程序都可以定义其他额外的函数。 您可以把代码划分到不同的函数中。如何划分代码到不同的函数中是由您来决定的,但在逻辑上,划分通常…...

关于如何创建一个windows窗口的exe文件
如何创建一个windows窗口exe文件,具体参照这个博主: http://t.csdn.cn/pfQK5 以下是实现代码,注意用vs打开: #pragma comment( linker, "/subsystem:\"windows\" /entry:\"WinMainCRTStartup\"" …...
re学习(33)攻防世界-secret-galaxy-300(动态调试)
下载压缩包: 下载链接:https://adworld.xctf.org.cn/challenges/list 参考文章:攻防世界逆向高手题之secret-galaxy-300_沐一 林的博客-CSDN博客 发现这只是三个同一类型文件的三个不同版本而已,一个windows32位exe࿰…...
springboot工程集成前端编译包,用于uni-app webView工程,解决其需独立部署带来的麻烦,场景如页面->画布->图片->pdf
前端工程 访问方式 http://127.0.0.1:8080/context/frontEnd/index放行 public class SecurityConfig extends WebSecurityConfigurerAdapter { "/frontEnd/**",SysFrontEndController import lombok.extern.slf4j.Slf4j; import nl.basjes.shaded.org.springfram…...
NeuralNLP-NeuralClassifier的使用记录(二),训练预测自己的【中文文本多分类】
NeuralNLP-NeuralClassifier的使用记录,训练预测自己的【中文文本多分类】 数据准备: 与英文的训练预测一致,都使用相同的数据格式,将数据通过代码处理为JSON格式,以下是我使用的一种,不同的原数据情况…...

express学习笔记8 - 文件上传 下载以及预览
一、上传 1、 安装multer (任意选其中一种) yarn add multer --S npm install multer --S 2、新建配置文件(utils/multerConfig) const multer require(multer); const mkdirp require(mkdirp); // const sd require(silly-datetime); const path require(path);con…...
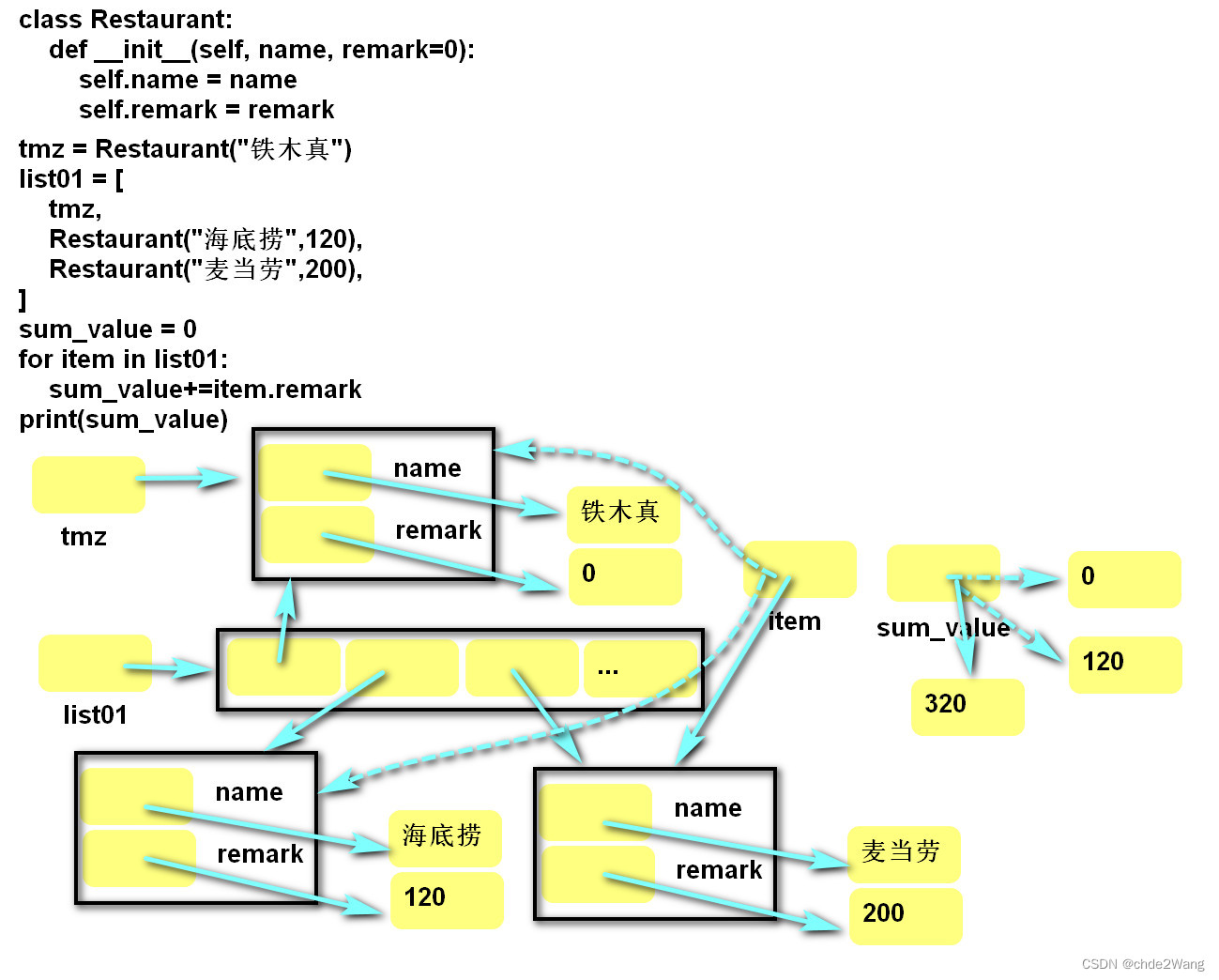
Python系统学习1-9-类(一)
一、类之初印象 1、类就是空表格,将变量(列名)和函数(行为)结合起来 2、创建对象,表达具体行 3、创建类就是创建数据的模板 --操作数据时有提示 --还能再组合数据的行为 --结构更加清晰 4、类的内存分配…...
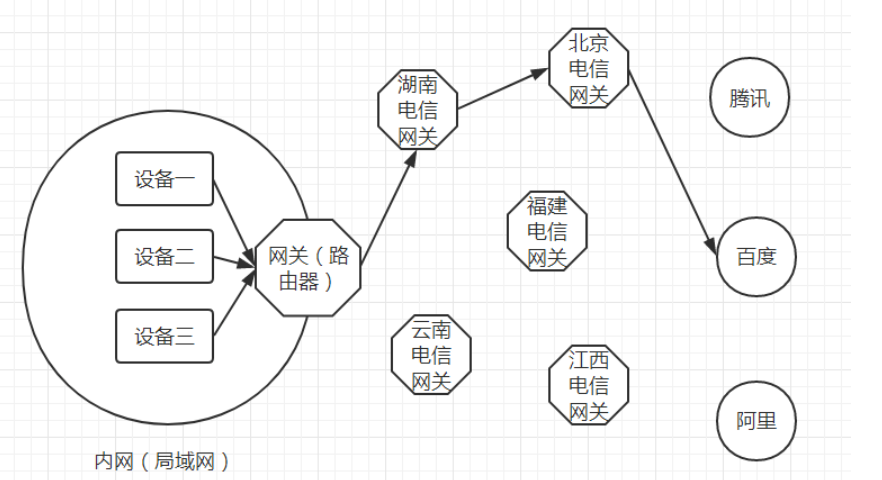
什么是公网、私网、内网、外网?
中午好,我的网工朋友。 最近经常有很多小白朋友在问,公网、私网、内网、外网,这些的概念是啥样的,又该怎么去界定。 关于IP地址,确实没有太明确的区分,其实也不必太过咬文嚼字。 内网、外网就是一个参考…...
一篇文章教会你搭建私人kindle图书馆,并内网穿透实现公网访问
搭建私人kindle图书馆,并内网穿透实现公网访问 在电子书风靡的时期,大部分人都购买了一本电子书,虽然这本电子书更多的时候是被搁置在储物架上吃灰,或者成为盖泡面的神器,但当亚马逊发布消息将放弃电子书在中国的服务…...
好用的安卓手机投屏到mac分享
工具推荐:scrcpy github地址:https://github.com/Genymobile/scrcpy/tree/master mac使用方式 安装环境,打开terminal,执行以下命令,没有brew的先安装brew brew install scrcpy brew install android-platform-too…...
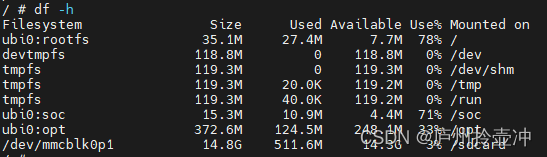
df -h
df -h 命令用于查看磁盘占用的空间 Filesystem:表示该文件系统位于哪个分区,因此该列显示的是设备名称; Used:表示用掉的磁盘空间大小; Available:表示剩余的磁盘空间大小; Use%:磁盘…...
彻底卸载Android Studio
永恒的爱是永远恪守最初的诺言。 在安装Android Studio会有很多问题导致无法正常运行,多次下载AS多次错误后了解到,删除以下四个文件才能彻底卸载Android Studio。 第一个文件:.gradle 路径:C:\Users\yao(这里yao是本…...

QT 5.12配置OpenCV3.4.10
主要过程:使用cmake编译源码,生成Mingw64位 下的OpenCV库 三篇博客解决问题: 1.Windows下安装Qt并使用cmake配置opencv3.4.10(含错误记录及解决办法)_d:\qt\qt5.14.2\5.14.2\mingw73_64\include\qtcore\qg_会飞的DA象的博客-CSDN博客 2.【…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...
